摘要:空氣信道中的陣列信號處理技術可以進行多個目標同時定位,經過適配后應用在水下信道中,可以實現水聲定位。空間信號到達方向是陣列信號處理的重要環節,利用特征結構的子空間方法確定相同范圍內一個或多個信號源的空間地理位置,常用的方法是 MUSIC 算法和 ESPRIT算法。在工程實踐中,多個陣元僅有有限路信號采集通道形成受限水聲陣列,在受限水聲陣列條件下,如何選取陣型,匹配相應算法,對水聲定位結果至關重要。選擇二維面陣,包括 L 陣型、雙 L 陣型、均勻面陣型、“口”字陣型,用數據進行仿真驗證,分析比較定位效果,結果表明不同陣型匹配相應算法,在定位精度或計算速度方面各有優缺點。針對不同工程需求,可以選取相應的陣型,對實踐提供了有效的參考依據。
0 引 言
常規的水聲定位系統一般利用時間差或者相位差的方法,一次只能完成一個目標的水下定位,無法實現在同一場景中同時定位多個目標。受到空氣信道中的陣列信號處理技術可以進行多個目標同時定位的啟發,經過適配后應用在水下信道中,就可以解決此問題。空氣信道無線電陣列信號處理技術歷經多年的發展,技術已經非常成熟,并且應用廣泛,比如在雷達、導航、通信等領域[1],陣列信號處理技術就是其中應用比較頻繁和成 熟 的 一 種 。空 間 信 號 到 達 的 方 向(Direction ofArrival,DOA)是呈現在陣列信號處理過程中的一個重要環節,目標是確定在相同范圍內一個或者多個信號源的空間地理位置。DOA 估計算法采用了特征結構的子空間方法,對數個空間信號到達的方向進行研究,滿足用戶需求,其分辨率的大小由瑞利限決定,也就是陣列長度及其間隔[2]。出現在超分辨率 DOA 估計算法中最早的兩種著名算法分別是 MUSIC 算法(及改進算法)和ESPRIT 算法,將空間譜估計技術向高分辨側技術推進,并且有了長足發展。
選擇匹配的陣列信號模型是陣列信號處理之前最關鍵的步驟。本文選擇了多個二維面陣模型,用 DOA估計算法分別加以驗證,從不同方面進行比較,給用戶提供客觀評價,方便在水聲定位工程實踐中選擇合適的信號處理方法。
1 受限水聲陣列
水聲定位系統硬件由多陣元水聽器陣列組成,后續沒有完成多路水聲信道建設,僅有有限路采集通道,形成了一種受限的水聲陣列陣型。為完成多目標定位,在硬件基礎上增加了通道選擇模塊,用來快速實現陣型變換。模塊采用 FPGA 芯片,采用 Verilog HDL 語言編寫代碼,設置陣型選擇模式,每個模式可以代表下文中所選的對應陣型。用運算放大器對采集到的模擬信號完成放大后,采用帶通濾波選擇相同的通帶頻率和工作頻率,保障各個信號通道基礎信息設置一致[3?4]。
2 二維面陣模型
為了簡化分析,更快速準確地得到仿真結論,假設采用的信號源形式為:點輻射源、窄帶信號,假定噪聲為高斯白噪聲,并且與信號源不相關,信號源的數量是已知的,也可以從計算中獲取,接收陣列與信號源之間是遠場環境。本文中應用的二維面陣有 L 陣型、雙 L 陣型、均勻面陣型、“口”字陣型,信源至陣列的俯仰角 θ 定義為原點到信源的方向矢量與 z 軸方向矢量間的夾角,方位角 ? 則是原點到信源的方向矢量在 x?y平面上的投影與 x 軸方向矢量之間的夾角[5]。信源與接收陣之間滿足遠場條件,故用一點表示整個陣列。L 陣型有 M + N - 1 個陣元,由 x 軸上 N 個陣元和 y軸上 M 個陣元均勻構成,陣元間距為 d。假設有 K 個信源,其 DOA 為 ( θk ,?k()k=1,2,…,K),其中 θk,?k 分別為第 k個信源的俯仰角和方位角。
雙 L陣型類似于 L陣型,結構圖如圖 1所示。
對于均勻面陣型,結構圖如圖 2 所示,陣元數為M × N,均勻分布在平面上。信源數為 K,θk,?k 分別代表第 k個信源的俯仰角和方位角。
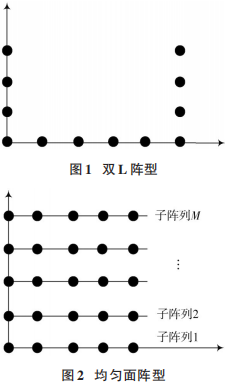
“口”字陣型即由 4 條線陣圍成一個矩形,方向矩陣雷同于雙 L陣型。
3 不同算法匹配陣型仿真比較
二維 DOA 估計本文采用 L 陣型、雙 L 陣型、均勻面陣型和“口”字陣型實現二維參數估計,多數二維 DOA算法是在一維 DOA 算法基礎上針對二維空間提出的改進或推廣方法[6]。二維 MUSIC 算法是二維 DOA 估計的典型算法。本文針對不同陣型選用不同適配算法:二維MUSIC、求根 MUSIC、ESPRIT 和降維 MUSIC 算法定義均方根誤差為[7]:
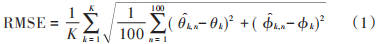
式中 θk, n 和 ?k, n 分別表示第n次蒙特卡洛仿真中的θk 和?k的估計值。
3.1 L陣型?MUSIC 和求根 MUSIC 算法
不同于一般兩邊等陣元數的 L 陣型,由于硬件限制,y 軸方向只有4 個陣元,x 軸就會有 9 個陣元,陣元數的不同使得兩個角度的測量誤差水平不同。2D?MUSIC算法利用空間譜函數進行二維的譜峰搜索,是一個經典的算法,具有普遍適用性,缺陷就是要進行空間二維角度搜索,運行時間長。求根 MUSIC 算法用多項式求根的方法代替譜搜索,能大大降低運算量[8]。
仿真條件:L 陣型,x 軸上有 9 個陣元,y 軸上有 4 個陣元,公用參考點陣元,假設 3個信號互不相干,角度[7]分別為(10°,20°),(30°,40°),(50°,70°),信噪比選用0 dB,5 dB,10 dB,15 dB,20 dB 和 25 dB。使用 MUSIC 和求根 MUSIC 算法,MUSIC 算法取 1°作為搜索步長。蒙特卡洛次數為 100,圖 3、圖 4 分別為 MUSIC 單次運算圖和求根 MUSIC 算法估計性能圖,信噪比均為 10 dB,快拍數為 200。
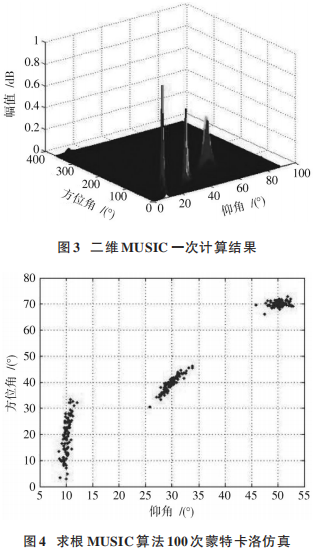
從圖 3、圖 4 可以看出,MUSIC 算法尖峰還是很明顯,求根 MUSIC 在低仰角時方位角誤差很大,甚至大于10°。在快拍數為 200,不同信噪比下,各算法均方根誤差對比如表 1所示。
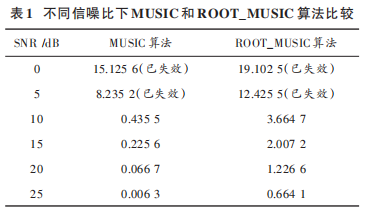
MUSIC 算法平均運算時間為 1.181 1 s,求根 MUSIC算法平均運算時間為 0.093 7 s。由表 1 可以分析出求根 MUSIC 算法由于不需要全空間搜索,所以計算時間短許多,但由于 y 軸上陣元數限制,均方根誤差偏大。MUSIC 算法運算時間過長,不適合實時運算,但精度高,適合事后回放。兩種算法均只能在信噪比大于 10 dB下才能發揮作用。
3.2 雙 L陣型?MUSIC 算法
雙 L 陣型呈 U 型,x 軸上有 6 個陣元,y 軸上有 2 組,每組 4 個陣元,公用參考點陣元,假設 3 個信號互不相干,角度分別為(10°,20°),(30°,40°),(50°,70°),信噪比 選 用 0 dB,5 dB,10 dB,15 dB,20 dB 和 25 dB。MUSIC 算法取 1°作為搜索步長,蒙特卡洛次數為 100。
在快拍數為 200,不同信噪比下,MUSIC 算法均方根誤差對比如表 2所示。

MUSIC 算法平均用時 2.743 9 s。原先考慮使用求根 MUSIC 算法作為比較,但仿真后發現 y 軸上 4 個陣元大大限制了該算法,使得求根 MUSIC算法經常得出錯誤的結果,因此不將求根MUSIC算法作為L陣型的比較。
3.3 均勻面陣型?MUSIC、降維 MUSIC 和 ESPRIT算法
由于測量通道有限,不能利用全部陣元,所以選取3×4 均勻面陣型作為比較對象,由于求根 MUSIC 算法對x 軸和 y 軸上陣元數量敏感,所以此次面陣算法采用MUSIC、降維 MUSIC 和 Unitary_ESPRIT 算法作為比較。降維算法優點有:可以實現配對的二維角度估計;只需一次一維局部搜索;運算量大大降低;完全利用信號子空間和噪聲子空間;角度估計性能非常接近 2D?MUSIC算法[9]。Unitary_ESPRIT 算法通過 Q 矩陣,將方向矩陣轉變為只有實部,從而降低運算復雜度。角度估計可以根據實部和虛部信息配對好,無需另行計算配對[9]。
仿真條件:均勻面陣型,x軸上有 4個陣元,y軸上有3 個陣元,呈 4×3 排布,假設 3 個信號互不相干,角度分別為(10°,20°),(30°,40°),(50°,70°),信噪比選用0 dB,5 dB,10 dB,15 dB,20 dB 和 25 dB。使用 MUSIC、降 維 MUSIC 和 ESPRIT 算 法 ,MUSIC 算 法 取 1° 作 為搜 索 步 長 ,降 維 MUSIC 選 取 0.001 精 度 作 為 搜 索 步長 。蒙 特卡洛次數為 100。圖 5~圖 7 分別為 MUSIC、Unitary_ESPRIT 和降維 MUSIC 算法估計性能圖,信噪比均為 10 dB,快拍數為 200。
快拍數為 200,不同信噪比下各算法均方根誤差比較如表 3所示。
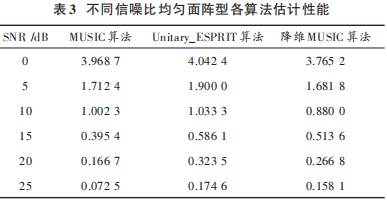
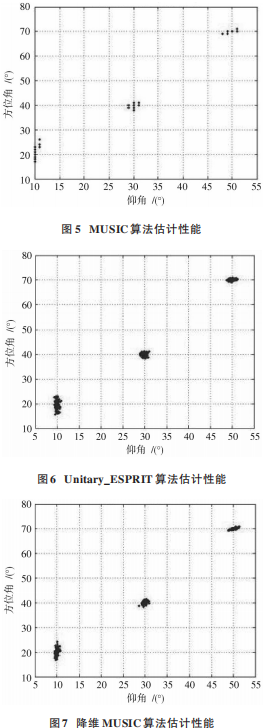
MUSIC 算 法 平 均 運 算 時 間 為 3.442 1 s,Unitary_ESPRIT 算法平均運算時間為 0.001 4 s,降維MUSIC 算法平均運算時間為 0.196 0 s。由表 3 可以分析出,MUSIC 算法精度高,但由于需要進行二維角度搜索,運算量很大,運算時間過長,不適合作為實時定位算法,而 Unitary_ESPRIT 通過 Q 矩陣,將方向矩陣轉變為只有實部,從而降低運算復雜度,并且根據實部虛部信息獲得配對好的角度估計[10]。降維 MUSIC 算法計算精度和搜索步長有關,類似于MUSIC算法,但只有一維搜索,所以計算總量相較MUSIC減少很多,高于Unitary_ESPRIT算法。
3.4 “口”字陣型?MUSIC 算法
“口”字陣型每邊為 4 個陣元,呈正方形排布,假設3 個信號互不相干,角度分別為(10°,20°),(30°,40°),(50°,70°),信噪比選用 0dB、5 dB、10 dB、15 dB、20 dB和 25 dB。MUSIC 算法取 1°作為搜索步長。蒙特卡洛次數為 100,快拍數為 200,不同信噪比下 MUSIC 算法均方根誤差比較如表 4所示。
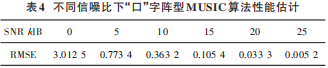
MUSIC 算法平均運算時間為 2.945 5 s。這種非常規陣型適配算法只能使用 MUSIC 算法。
3.5 二維面陣陣型適應算法比較
以上分小節介紹了各陣型組成及各陣型下不同算法性能,在快拍數為 200,不同信噪比下綜合各陣型各算法均方根誤差結果如圖 8 所示,各陣型算法用時如圖 9所示。
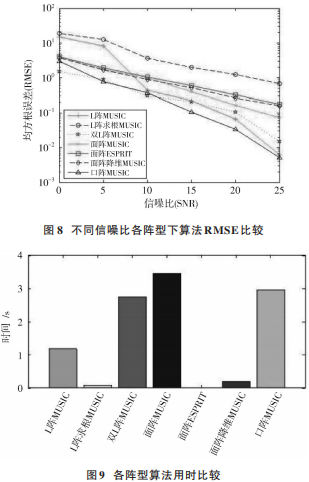
從圖 8可以得出以下結論:
1)“口”字陣型 MUSIC 算法和雙 L 陣 MUSIC 算法在所比較的各陣型算法中均方根誤差最優,這與該兩種陣型所圍成的面積最大有關;
2)均勻面陣型三種算法沒有表現很大的差距;
3)求根 MUSIC 在各陣型中表現不佳,甚至在其他陣型下無法計算出正確的結果,這與 y 軸最多只有 4 個陣元有很大的關系。
由圖 9 可以看出,面陣 MUSIC 算法用時最長,因為每 次 循 環 均 會 計 算 Kronecker 積 ,所 以 較 其 他 陣 型MUSIC 用時較長。均勻面陣型 ESPRIT 用時最短,可達毫秒級,求根 MUSIC 和降維 MUSIC 算法用時大幅低于MUSIC 算法。綜合各算法均方根誤差,MUSIC 算法精度高、用時最長,不適合實時計算,可用于事后數據分析,使 用 更 高 性 能 計 算 機 提 高 計 算 速 度 。 L 型 陣 求 根MUSIC 是精度最差的,面陣 ESPRIT 和降維 MUSIC 計算精度相差不大,所以選取運行時間更短的面陣 ESPRIT算法作為系統實時定位算法,相對應的系統陣型為 4×3均勻面陣型。
綜合以上仿真可得出結論:當信號源深度不定時,可采用均勻面陣型的形式,使用 ESPRIT 算法實時解算仰角和方位角。當需要更高精度和不需要實時計算時,可采用“口”字陣型列采集數據,使用更快計算速度的計算機,采用 MUSIC 算法進行更高精度解算。
4 結 論
本文分別采用二維 MUSIC、求根 MUSIC、ESPRIT 和降維 MUSIC 算法,選取合適的二維面陣陣型,進行二維DOA 估計,用仿真數據加以驗證,對比不同算法匹配相應陣型各自的優缺點,在實用性、計算優勢和定位精度上各有不同,用戶在使用時可以根據實際情況選擇最佳方案。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4600瀏覽量
92647 -
陣列
+關注
關注
0文章
60瀏覽量
16833 -
MUSIC
+關注
關注
0文章
30瀏覽量
7407
原文標題:受限水聲陣列陣型定位算法比較研究 | 論文速覽
文章出處:【微信號:現代電子技術,微信公眾號:現代電子技術】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
安泰功率放大器在水聲測試中的應用有哪些

高壓放大器在寬帶水聲陣列信號研究中的應用
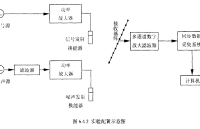
高壓放大器模塊在平面水聲壓電換能器研究中的應用
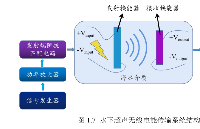
基于COOT算法的局部陰影下光伏陣列MPPT控制研究
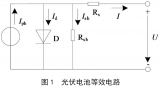
ATA-L8水聲功率放大器在石油勘探中的應用研究

IP地址定位與GPS定位:技術解析與應用比較
面陣相機的工作原理 線陣相機和面陣相機的區別在哪
寬帶放大器在CMUT陣列的超聲反射成像研究中的應用
水聲功率放大器在水聲通信技術研究中的具體應用

目前的室內定位算法有什么優勢
Aigtek水聲學分會2023年學術交流會圓滿收官





 受限水聲陣列陣型定位算法比較研究
受限水聲陣列陣型定位算法比較研究











評論