矢量分析是學(xué)習(xí)《電磁波與電磁場》《電動(dòng)力學(xué)》，必備的數(shù)學(xué)技能。電磁波和電磁場的理解，對我們學(xué)習(xí)射頻的相關(guān)知識是根基。但是，很多朋友在碰到矢量計(jì)算的時(shí)候，都是百爪撓心。用語言去描述麥克斯韋方程組都神頭鬼臉，來個(gè)方程解一下，或者推到個(gè)公式都抓瞎。

這是為什么呢？

原因1、學(xué)習(xí)路徑長，激勵(lì)反饋周期長


首先，我們完全理解和學(xué)會(huì)的路徑比較長，也就是說，他本身就不是很容易學(xué)習(xí)的內(nèi)容。體會(huì)到學(xué)習(xí)成果的激勵(lì)反饋比較慢。

也是我們學(xué)習(xí)的最大障礙，我們可以連續(xù)一個(gè)小時(shí)很愉快的嗑瓜子，但是很難連續(xù)一個(gè)小時(shí)愉快的學(xué)習(xí)。

能磕一個(gè)小時(shí)無壓力。我們換個(gè)規(guī)則，現(xiàn)在你只能磕，不能吃，瓜子仁留下來。磕一個(gè)小時(shí)，才把瓜子仁一次吃完。是不是有點(diǎn)無趣了？同樣的時(shí)間，瓜子仁也沒少吃，為什么感覺變了？

很多大事情，都是由一個(gè)個(gè)小事務(wù)重復(fù)或迭代而成，每個(gè)小事務(wù)中，包含了反饋和校正。反饋的周期越短，越為容易上手。磕瓜子容易，因?yàn)樵趦擅雰?nèi)就能得到反饋。而學(xué)習(xí)難，因?yàn)閷W(xué)習(xí)的反饋周期長。

一個(gè)典型的學(xué)習(xí)周期是這樣：學(xué)習(xí)，思考，應(yīng)用，校正。這個(gè)周期越短，學(xué)習(xí)就越輕松。合理的安排學(xué)習(xí)計(jì)劃，縮短學(xué)習(xí)周期，同樣的東西，可以學(xué)得更高效，輕松。

如果我們學(xué)習(xí)一個(gè)簡單的東西，越直觀的東西越容易學(xué)會(huì)，往往容易獲得成就感，大家也愿意學(xué)，愿意用。比如說：老年人學(xué)習(xí)用電腦學(xué)了N長時(shí)間，也學(xué)不會(huì)，沒法理解《我的電腦》、《注冊表》、《控制面板》等等，很快就放棄使用電腦了，不愿意用電腦，不愿意去理解電腦。但是老年人、小朋友很容易學(xué)會(huì)使用。

我們?nèi)プ觥笆噶糠治觥钡臅r(shí)候，為什么困難呢？因?yàn)槲覀兏邤?shù)學(xué)習(xí)的內(nèi)容在大一考完試的時(shí)候已經(jīng)還給老師了。或者考試靠背題，背完就忘記了。

沒有人幫我們分解，我們學(xué)習(xí)這門課，需要哪些數(shù)學(xué)知識。必備的數(shù)學(xué)知識，在學(xué)習(xí)的時(shí)候，并沒有人告訴我們這些事有用的，或者未來可能做什么用。（而科學(xué)家在發(fā)明數(shù)學(xué)工具的時(shí)候，是有某些目的的發(fā)明的）。

當(dāng)同學(xué)們發(fā)現(xiàn)，屮艸芔茻，當(dāng)年高數(shù)就是糊弄過去的，你現(xiàn)在讓我復(fù)習(xí)明白？就選擇繼續(xù)糊弄這門課了。。。。

根據(jù)這樣的知識體系需求，按需學(xué)習(xí)，減少學(xué)習(xí)量，避免學(xué)習(xí)周期過長，而囫圇吞棗，或者半途而廢。

根據(jù)大家的大多數(shù)人的情況，不建議選擇不講述數(shù)學(xué)概念的電磁波的書籍。例如這本：

原因2 早期的一些概念誤導(dǎo)，你需要清理自己的大腦內(nèi)存。

在高中數(shù)學(xué)時(shí)，兩個(gè)字母相乘，中間放個(gè)點(diǎn)、放個(gè)X、什么都不放，是一個(gè)意思。這里其實(shí)對于大多數(shù)學(xué)生來說，理解沒有什么障礙，但是在表達(dá)習(xí)慣上，帶來了嚴(yán)重的困擾。

也就是在推導(dǎo)計(jì)算的過程中，有的朋友已經(jīng)習(xí)慣了兩個(gè)數(shù)相乘，中間放個(gè)點(diǎn)。但是此點(diǎn)、非彼點(diǎn)。寫多了，就亂了，自己也糊涂了。到底是是矢量還是標(biāo)量？到底是“點(diǎn)乘”還是“乘以”。

所以，我們需要在這方面做一些訓(xùn)練，在表達(dá)上面，需要區(qū)分“點(diǎn)乘”、“叉乘”、“標(biāo)量相乘”，因?yàn)樗麄兙哂胁煌奈锢砗x，不同的數(shù)學(xué)計(jì)算方法。

原因3、課本中往往只生硬的介紹數(shù)據(jù)概念，不解釋物理應(yīng)用

這里比較典型的是“點(diǎn)乘”、“叉乘”的概念。

有些課本往往直接給你拍個(gè)公式，讓你很茫然。

點(diǎn)積

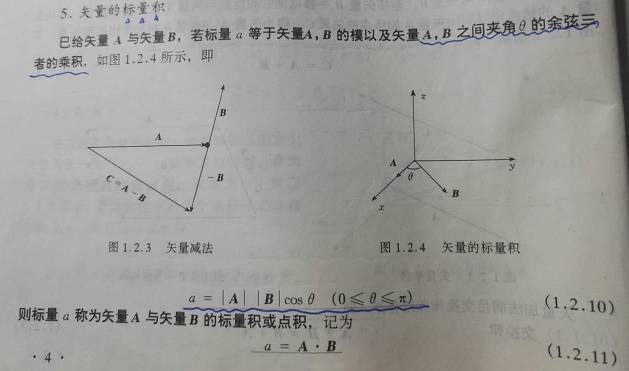
叉積

這樣的新概念扔給你，一定是一臉懵B。有毛用？我為什么要掌握它？

但是如果，先幫你回憶一下“做功”的計(jì)算過程：

W=FS cosθ 中S是位移，要與路程區(qū)別開來。例如，一個(gè)人從地面提起物體又放回原地，那么重力所做的功是多少呢？因?yàn)槲矬w又放回原地了，物體位移的大小為零，所以W=0。

那么這里：位移是一個(gè)矢量、力也是一個(gè)矢量。我們以前計(jì)算的時(shí)候，其實(shí)是把這兩個(gè)物理量先簡化為標(biāo)量，然后看夾角。但是我們現(xiàn)在升級了，現(xiàn)在要區(qū)分標(biāo)量和矢量。這兩個(gè)物理量，以及計(jì)算，直接就標(biāo)示為：

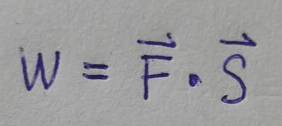
力有方向、位移也有方向。但是兩者綜合出來的結(jié)果，功，沒有方向，是一個(gè)標(biāo)量。而且這個(gè)計(jì)算結(jié)果，是W=FS cosθ ，符合我們原來的認(rèn)知；

實(shí)際對于物理量的理解：力量與位移一致的方向上才做功，上圖中小聰做了不少無用功，小明相對省功。這一計(jì)算過程其實(shí)是：力量在位移方向的投影，這個(gè)cosθ可以看做是一個(gè)投影的過程。

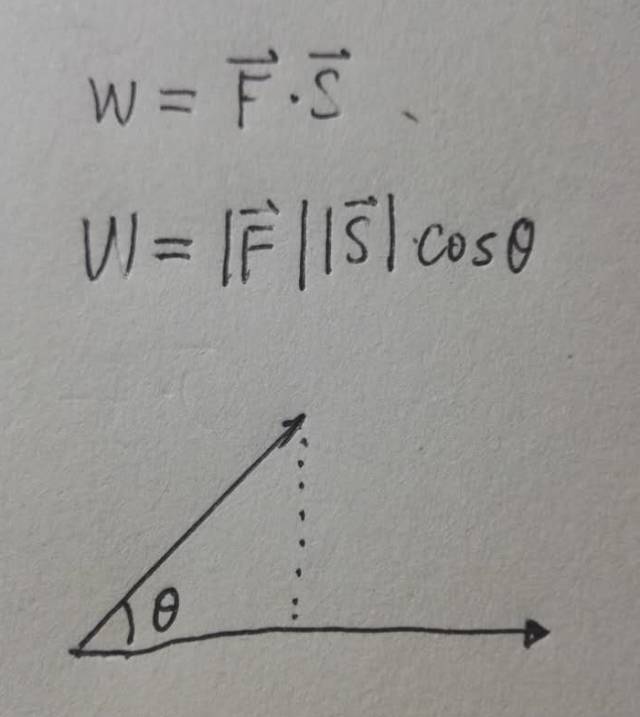
上面的概念并不難理解，但是我為什么羅里吧嗦說半天呢？

啟迪未知事物的探索，引導(dǎo)已知事物的深入了解

我們應(yīng)該從我們已經(jīng)掌握的知識點(diǎn)出發(fā)，去拓展新知識，形成完整的知識體系，形成更高層次的認(rèn)知，而不是只是灌輸一些新的概念，然后讓學(xué)習(xí)者去記憶。

同樣的“叉積”，我們也應(yīng)該找一個(gè)形象的物理模型：

洛倫茲力

在電動(dòng)力學(xué)里，洛倫茲力（Lorentz force）是運(yùn)動(dòng)于電磁場的帶電粒子所受的力。根據(jù)洛倫茲力定律，洛倫茲力可以用方程，稱為洛倫茲力方程，表達(dá)為

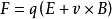
其中， F是洛倫茲力， q是帶電粒子的電荷量，E是電場強(qiáng)度， v是帶電粒子的速度， B是磁感應(yīng)強(qiáng)度。

洛倫茲力定律是一個(gè)基本公理，不是從別的理論推導(dǎo)出來的定律，而是由多次重復(fù)完成的實(shí)驗(yàn)所得到的同樣的結(jié)果。

感受到電場的作用，正電荷會(huì)朝著電場的方向加速；

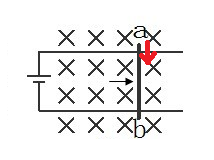
根據(jù)上面的公式：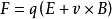

我們按照“叉積”的右手定則，四指先指向電流的方向，然后彎向磁場方向，就得到了力的方向。

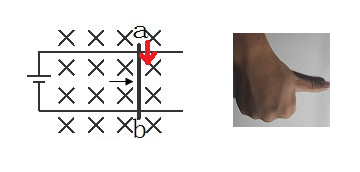
有的朋友要提出了：“洛倫茲力不是左手定律么？”這里用“叉積”的時(shí)候，怎么又變成了右手定律？此處我們一定要像印度友人一樣，分得清左右手。右手用于手抓飯，左手做其他事情。。。。

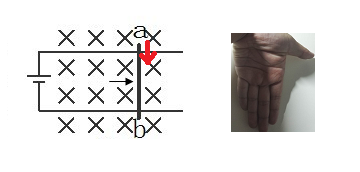
此處，我們用了“vXB”叉積的表達(dá)方式之后，我們可以忘記我們的左手。

再舉個(gè)例子：梯度。

某書中的描述，又過于口語化表達(dá)，弄得讀者很是糊涂：

首先什么是“最快”？為什么max值。

就是需要理解“點(diǎn)乘”的最大值，是兩個(gè)矢量方向一致，這樣上述投影才會(huì)是最大的。

假設(shè)你站在一個(gè)山上四處遙望，發(fā)現(xiàn)最陡的方向，就是梯度的方向。

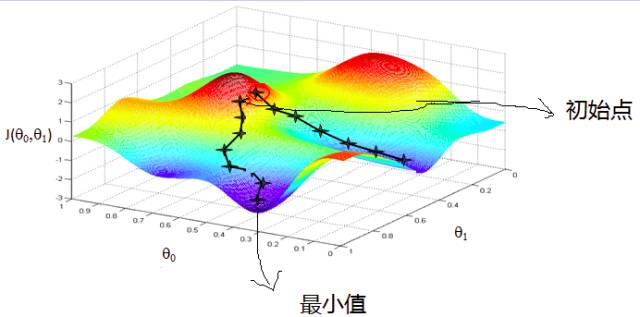
其實(shí)，幫助大家更利于理解一些概念，需要用一些文科生思維，去描述和解釋一些理科現(xiàn)象和公式，講現(xiàn)象與公式結(jié)合起來，才能夠形成這種深刻理解，或者說這種強(qiáng)力記憶點(diǎn)。

因?yàn)椴皇敲總€(gè)人都是數(shù)學(xué)天才，也不是每個(gè)人看到一個(gè)概念就能理解，理解一個(gè)概念就能夠記住。需要我們通過具象思維，去解釋和關(guān)聯(lián)一些抽象思維。

否則就成了背題背概念，這種悲劇了。

原因4 書本與書本之間的用語、表達(dá)方式不統(tǒng)一

例如 矢量的表達(dá)方式，三本書，三種表達(dá)方式。

在《高等數(shù)學(xué)》同濟(jì)大學(xué)數(shù)學(xué)教研室，這本書講的是 向量，向量場；而在所有的電磁場、電動(dòng)力學(xué)的課本里面，又使用 矢量、矢量場。同時(shí)，在《高等數(shù)學(xué)》的課程中，并沒有漢密爾頓算子的介紹。

這里需要說的，就是某些大學(xué)的課程體系不成熟。課程設(shè)置的先后順序，教材選擇的合理性，需要優(yōu)化。

原因5 想象能力

矢量分析，說到底是需要三維想想能力的。

說個(gè)簡單的，矢量的加減法，你是否能夠在腦海里面復(fù)現(xiàn)，三維坐標(biāo)。當(dāng)解釋梯度、散度、旋度的時(shí)候，你是否腦海里面浮現(xiàn)對應(yīng)的場景？

其實(shí)矢量分析對想象能力、特別是空間想象能力還是有很高的要求的。

愛因斯坦憑借思想實(shí)驗(yàn)，完成了狹義相對論、廣義相對論的

火車思想實(shí)驗(yàn)：狹義相對論的精髓

理解狹義相對論的關(guān)鍵，是同時(shí)性的相對性。愛因斯坦正是通過火車思想實(shí)驗(yàn)實(shí)現(xiàn)這一目的的。在火車思想實(shí)驗(yàn)中，愛因斯坦設(shè)想，有一列很長的火車，正在以一恒定的速度v沿著一直線軌道行駛。該火車的兩端分別為A和B，其中間點(diǎn)為M。火車從A向B方向行進(jìn)（即A為車尾，B為車頭）。同時(shí)假定，在某一時(shí)刻t，與火車處于相同位置的鐵軌也存在三點(diǎn)A’、B’和M’（三點(diǎn)分別對應(yīng)于A、B和M）。A’和B’處分別有燈L1和L2，并且L1和L2在t時(shí)刻同時(shí)打開。那么，L1和L2的光線到達(dá)火車中間點(diǎn)M處（假定在t時(shí)刻，M點(diǎn)和M’點(diǎn)是重合的）的時(shí)間孰先孰后，還是同時(shí)到達(dá)？

電梯思想實(shí)驗(yàn)：廣義相對論的拓展

狹義相對論是以四維平直空間中的勻速直線運(yùn)動(dòng)為考察對象的，適用于一切慣性系，但無法說明非慣性系中的運(yùn)動(dòng)現(xiàn)象。為了克服狹義相對論的不足，將狹義相對論推廣到具有加速度的非慣性系中，愛因斯坦運(yùn)用了電梯思想實(shí)驗(yàn)為人們打開思路。

在一理想的摩天大樓的頂上，有一正在下降的電梯。在該電梯內(nèi)，有一物理學(xué)家在做實(shí)驗(yàn)。突然，電梯的鋼纜斷了，于是，電梯便處于自由落體狀態(tài)向地面降落。在降落的過程中，電梯內(nèi)的實(shí)驗(yàn)者，拿出一塊手帕和一只表，然后松開雙手。這兩個(gè)物體會(huì)怎樣運(yùn)動(dòng)呢？電梯外的觀察者以地球作為參考系，他會(huì)發(fā)現(xiàn)：手帕、表和電梯連同它的天花板、四壁、地面以及里面的實(shí)驗(yàn)者等，都以同樣的加速度下落。而電梯里面的實(shí)驗(yàn)者則會(huì)以電梯作為參考系，因?yàn)橐鲈谶@一參考系之外而不被考慮，他會(huì)發(fā)現(xiàn)手帕和表由于不受到任何力的作用，而處于靜止?fàn)顟B(tài)。在等效原理的幫助下，電梯思想實(shí)驗(yàn)告訴我們，引力場和加速度是相等的。廣義相對論成功地拓展到了非慣性系中。

原因6 根因 社會(huì)導(dǎo)向

大多數(shù)希望把這些概念搞清楚，搞懂的目的，并不是未來我要用，或者說我在其中獲得樂趣。在學(xué)校期間，很多同學(xué)沒搞懂的原因是，不搞懂，不搞明白，一樣是考試前突擊背題。

也有一些在校的學(xué)生問我，為什么要懂這些，反正未來也用不著。其實(shí)不然，如果你希望未來承載更高層次的工作，你的數(shù)理能力決定了你的高度。

假設(shè)你做嵌入式編程，你需要掌握C語言等基本技能，但是如果需要你實(shí)現(xiàn)一些信號處理的算法，你光會(huì)C語言、熟悉單片機(jī)，就明顯不夠了。需要你掌握更多的數(shù)理知識，矩陣運(yùn)算、偏微分方程、等等數(shù)學(xué)知識的儲(chǔ)備有顯得尤為重要。

另外，具體就不知道高校里面對老師是否把學(xué)生教會(huì)了，這個(gè)點(diǎn)，是如何考察的？

審核編輯 ：李倩