做過數(shù)據(jù)采集或者模擬電路的同學很可能知道下面這個關于ADC信噪比的著名公式:

其中N是ADC的位數(shù),比如對于一個10bit的ADC,N=10,當ADC采集一個滿量程的正弦波時,那么信噪比SNR=6.02*10+1.76=61.96dB,那么這個公式是怎么來的呢?
ADC量化噪聲
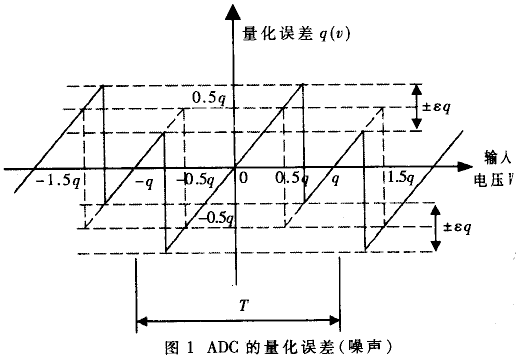
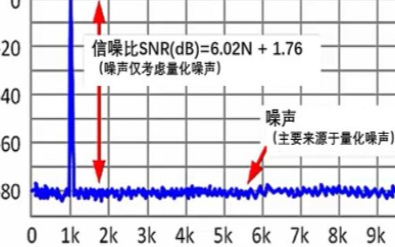
下圖是理想ADC的量化噪聲示意圖,從下圖可以看到,對于一個線性輸入的模擬信號,ADC會產(chǎn)生臺階式的輸出,這個輸入和輸出的誤差波形近似于一個峰峰值q=1LSB的鋸齒波,它的有效值RMS計算過程見公式(2)(q=1LSB),LSB計算過程見公式(3),其中FS是ADC的輸入電壓范圍,。


SNR
以前的文章介紹過SNR計算過程,信噪比是信號的有效值(RMS)除以噪聲的有效值(RMS),

對于一個滿量程輸入的正弦信號見公式(5),根據(jù)公式(5)可以求得公式(6),

對于滿量程ADC而言,其輸入范圍是0-FS,那么輸入的正弦信號的幅度范圍就是0-Fs/2,見下圖示意圖,因此公式(5)中的分母是2

ADC信噪比SNR與位數(shù)N
那么到目前為止,我們知道了信號的有效值(RMS),即公式(6),也知道了ADC量化噪聲的有效值(RMS),即公式(2)。把公式(6)和公式(2)帶入公式(4)得到公式(7):

公式(7)不夠簡化,我們繼續(xù)化簡(高中學的指數(shù)運算規(guī)則),可以得到公式(8),
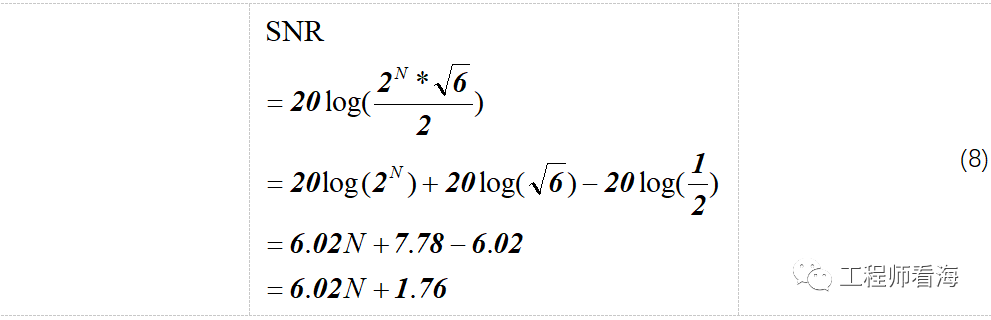
由此我們就推導出了ADC位數(shù)N與信噪比SNR的關系,是不是和公式(1)一模一樣?
多說幾句
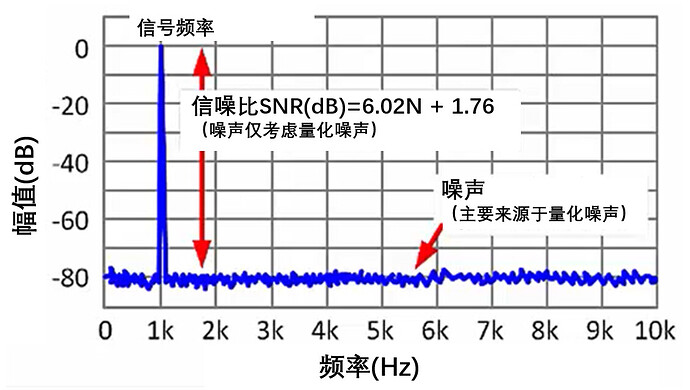
上式的成立條件是信號帶寬比較高。
如果信號帶寬(或者說頻率)很低,低于奈奎斯特采樣頻率fs/2,那么這會導致信號帶寬范圍內(nèi)的噪聲減小,進而使得SNR增加。
這就是常說的 過采樣 ,詳細內(nèi)容后面后機會在介紹。
另一點值得說明的是,在評估噪聲時,常用到頻譜分析,頻譜的本底噪聲值與采樣點數(shù)量有關。
如果采樣點多,那么本底噪聲就會低,如果采樣點數(shù)量減小,那么本底噪聲就會增加,這被稱為 FFT增益 。
因此在噪聲分析時,最好要自始至終使用相同數(shù)量的采樣點進行分析,避免被不正確的評估方法誤導。
審核編輯:劉清
-
模擬電路
+關注
關注
125文章
1554瀏覽量
102680 -
adc
+關注
關注
98文章
6438瀏覽量
544106 -
信噪比
+關注
關注
3文章
253瀏覽量
28593 -
RMS
+關注
關注
2文章
137瀏覽量
35751
發(fā)布評論請先 登錄
相關推薦
詳解ADC的信噪比公式
信噪比SNR、信號質(zhì)量RSSI的定義及公式

adc3101的采樣率由什么來決定呢?

ADC信噪比的分析及高速高分辨率ADC電路的實現(xiàn)
ADC測溫公式實用測溫工具資料免費下載
信噪比公式及解析
過采樣:提高ADC信噪比巧妙方法




 ADC信噪比的著名公式是怎么來的呢?
ADC信噪比的著名公式是怎么來的呢?
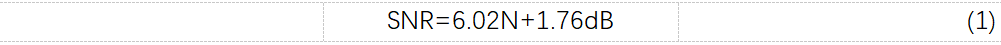



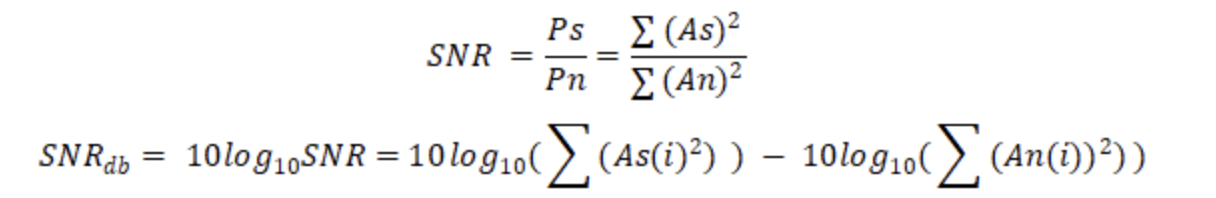










評論