大學微積分

大學微積分轉化是Mathematica最初的成就之一。但直到現在，我們仍在繼續增加新功能，將微積分變得更加簡單，也能更快地連接到其他應用。我們一直有D函數，可以在某處求導。在13.1版本，我們增加了ImplicitD，可以進行隱函數求導。

例如，它可以求xy關于x的導數，其中y由約束條件x2 + y2 =1的隱式決定：

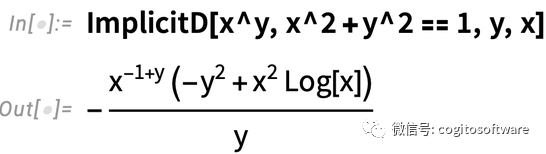
省略第一個參數，會得到標準大學微積分“求曲線切線的斜率”：

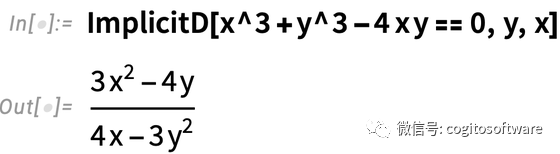
到目前為止，以上所有都是對長期存在的微積分功能簡單直接的重新整理。確實，這些隱函數求導功能在Wolfram|Alpha中已經存在很長時間了。但是對于Mathematica和Wolfram語言來說，我們希望每個功能都能盡可能普遍，也是為支持出現在微分幾何中的內容以及微分方程隱式解的漸進和驗證。除了常規的大學微積分之外，ImplicitD也可以做其他事情，比如，在由兩個曲面的焦點定義的曲線上，求二階隱式的導數：

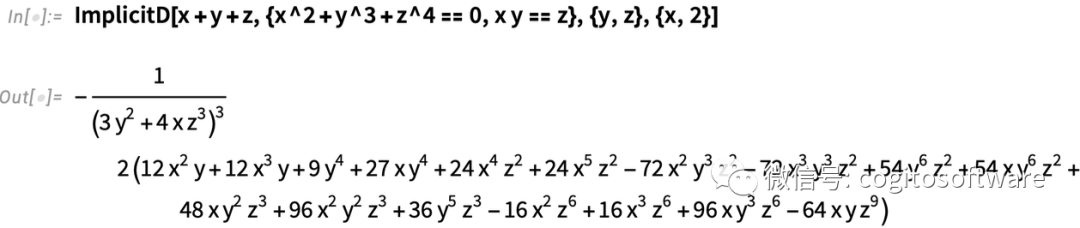
在Mathematica和Wolfram語言中，Integrate函數可以給你答案。(在Wolfram|Alpha中也可以得到分步計算過程。)但出于課程目的——或有時突破可能界限時——分步求解積分是非常有用的。所以在13.1版本中，我們添加了IntegrateChangeVariables函數，用于改變積分中的變量。有個直接的問題：如果用Integrate[...]函數指定積分，Integrate會繼續進程計算該積分：

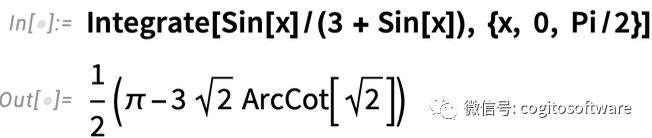
但是如果要用IntegrateChangeVariables，則需要一個“未完成”的積分。可以通過使用Inactive達到這一目的，例如：

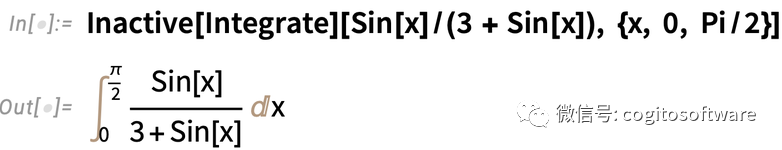
基于這一未轉換形式，可以使用IntegrateChangeVariables進行“三角代換”：

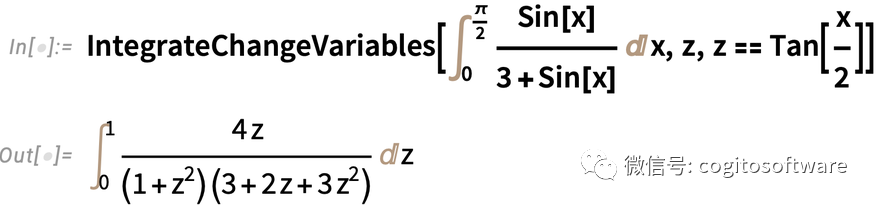
結果又是未轉換的形式，但以不同的方式闡述積分。Active繼續進行，并計算積分：

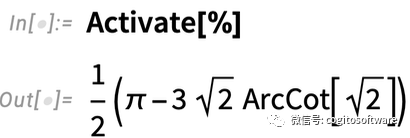
IntegrateChangeVariables可以處理多重積分——但要與命名的坐標系相結合。以下是將雙重積分轉換為極坐標：

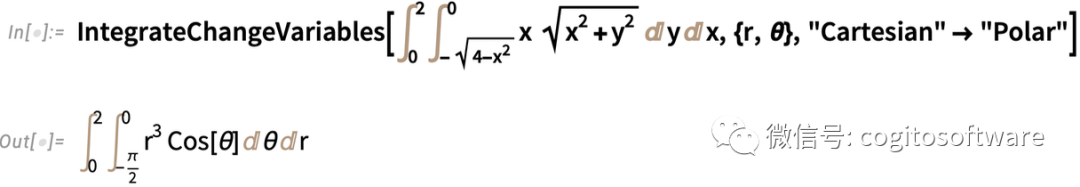
盡管積分變量的基本“結構”轉換非常直接，但IntegrateChangeVariables相關的內容還是非常復雜的。大學微積分變量的改變常常經過精心編排，從而更容易算出來。在常規情況下，IntegrateChangeVariables最終要對幾何區域進行重要轉換，在某些約束條件下難以簡化被積函數等等。

除了在積分中改變變量，13.1版本還引進了DSolveChangeVariables，用于改變微分方程中的變量。以下是將拉普拉斯方程轉化為極坐標的過程：

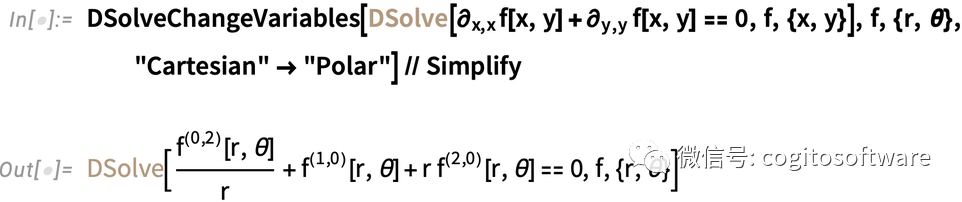
有時改變變量非常簡便。但有時(比如廣義相對論)可能導出完全不同的系統視圖。比如，以下是指數變換將普通的柯西-歐拉方程轉換為有常數系數的形式：

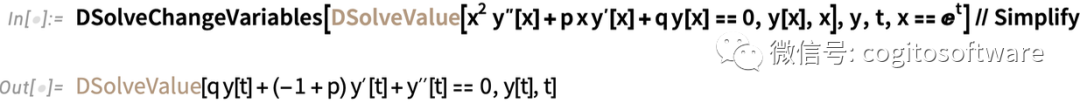
分數階微分

x2的一階導數是2x;二階導數是2。那么二分之一階導數是多少?即使在微積分出現的最初幾年，這一問題也經常被問到(例如萊布尼茨)。到19世紀，黎曼和劉維爾給出了答案，在13.1版本中，也可以用新函數FractionalD來計算：

計算另一個二分之一階導數，會回到一階導數：

在更普遍的情況下，有：

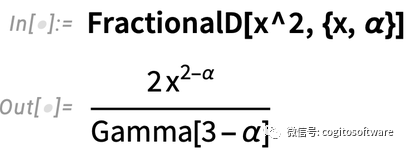
對于負階導數也可用，所以，例如，-1階導數是它的不定積分：

計算分數階導數與計算分數階微分一樣困難。但是FractionalD依然可以做到

即使結果可能會變得非常復雜：

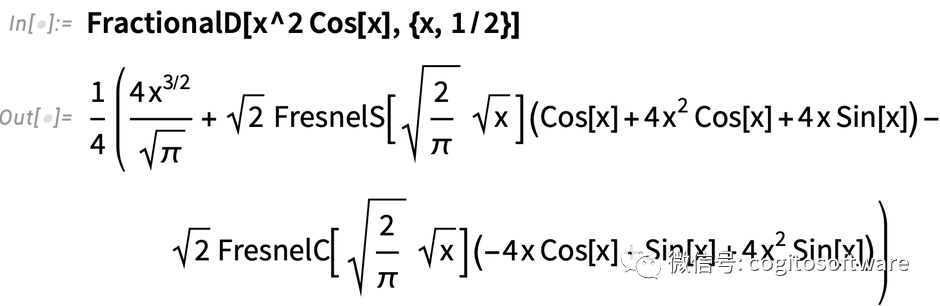
為什么FractionalD是一個單獨的函數，而不是D函數的衍生部分?我們討論過很多次這個問題。我們引入明確的函數FractionalD是因為分數階導數沒有一個明確的定義。事實上，在13.1版本中，我們也支持卡普托分數階導數(或差分積分)CaputoD。

對于x2的二分之一階導數，答案還是一樣：

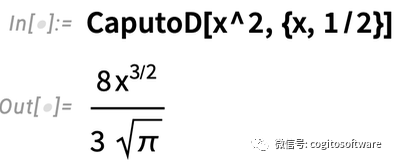
但只要函數在x =0處不為0，答案可能會有所不同：

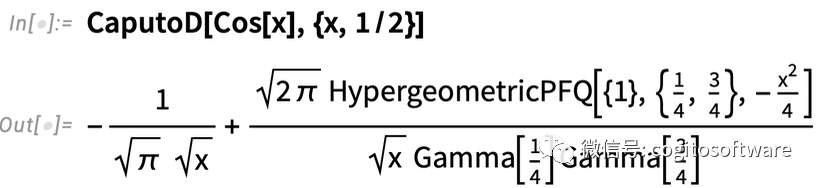
在處理拉普拉斯變換和微分方程時，CaputoD是分數階微分非常方便的方法。在13.1版本中，我們可以計算CaputoD，也能進行積分變換并求解涉及它的方程。

以下是二分之一階微分方程

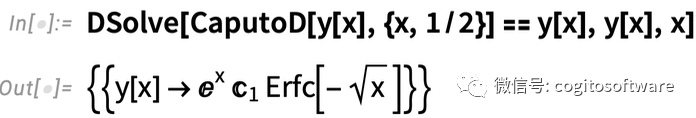
以下是二分之三階微分方程

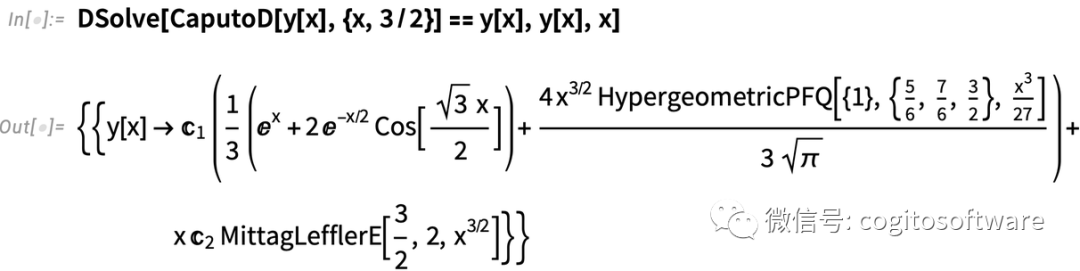
以及π階微分方程：

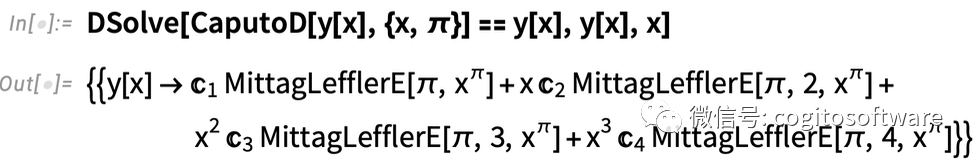
注意MittagLefflerE。這一函數(出現于9.0版本)對于分數階導數起的作用與Exp對于普通導數的作用一樣。

審核編輯：湯梓紅