導讀

本文介紹了幾個常見的匹配算法，通過算法過程和算法分析介紹了各個算法的優缺點和使用場景，并為后續的搜索文章做個鋪墊；讀者可以通過比較幾種算法的差異，進一步了解匹配算法演進過程以及解決問題的場景；KMP算法和Double-Array TireTree是其中算法思想的集大成者，希望讀者重點關注。

01

前言

上文探究了數據結構和算法的一些基礎和部分線性數據結構和部分簡單非線性數據結構，本文我們來一起探究圖論，以及一些字符串模式匹配的高級數據結構和算法。《搜索中常見數據結構與算法探究（一）》

搜索作為企業級系統的重要組成部分，越來越發揮著重要的作用，ES已經成為每個互聯網企業必備的工具集。而作為搜索的基礎部分，文本匹配的重要性不言而喻。文本匹配不僅為精確搜索提供了方法，而且為模糊匹配提供了算法依據。比如相似度算法，最大搜索長度算法都是在匹配算法的基礎上進行了變種和改良。

02 圖論基礎

2.1 圖的基本概念

一個圖G（V，E）由頂點的集V和邊的集E組成。每一條邊就是一副點對（v，w），其中v，w∈V。如果點對是有序的，那么圖就是有向圖。有時候還有第三種成分，稱作權。

以物流的抽象模型為例：每個配送中心是一個頂點，由兩個頂點表示的配送中心間如果存在一條干線運輸線，那么這兩個頂點就用一條邊連接。邊可以由一個權，表示時間、距離和運輸的成本。可以迅速確定任何兩個配送中心的最佳線路。這里的“最佳”可以是指最少邊數的路徑，也即經過的配送中心最少；也可以是對一種或所有權總量度所算出的最佳者。

2.2 圖的表示方法

考慮實用情況，以有向圖為例：

假設可以以省會城市開始對頂點編號。如下圖

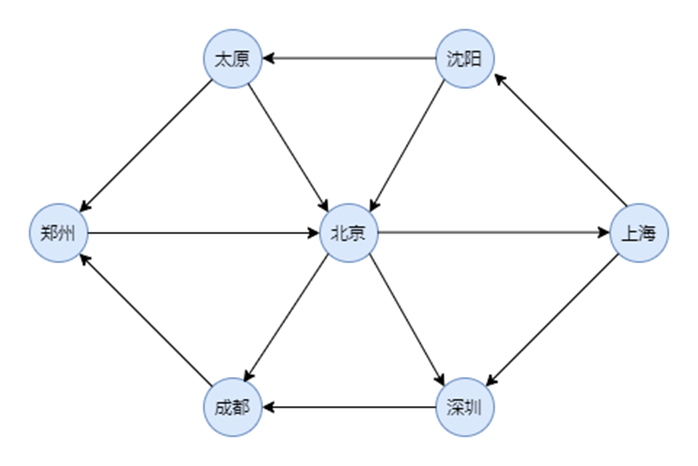
圖1有向圖圖示

1.鄰接矩陣

表示圖的一種簡單的方法是使用一個二維數據，稱為鄰接矩陣表示法。有一個二維數組A，對于每條邊（u，v），置A[u][v]等于true；否則數組元素就是false。

如果邊有一個權，那么可以置A[u][v]等于該權，而使用很大或者很小的權作為標記表示不存在的邊。雖然這種表示方法的優點是簡單，但是，它的空間復雜度為θ（|V|^2）,如果圖的邊不是很多（稀疏的），那么這種表示的代價就太大了。代碼如下：

/**
 * 

 * Description: 使用鄰接矩陣的圖表示法
 * 

 * Company: 京東
 *
 * @author pankun8
 * @date 2021/11/11 15:41
 */
@Data
@NoArgsConstructor
public class Graph{
    /**
     * 圖的節點數
     */
privateintn;


    /**
     * 圖
     */
privateT[]data;


    /**
     * 是否是有向圖
     */
privateBooleandirected;


    /**
     * 鄰接矩陣
     */
    private int[][] matrix;


    public Graph(T[] data , Boolean directed){
        this.n = data.length;
        this.data = data;
        this.directed = directed;
        matrix = new int[n][n];
    }


    public void init(T[] data , Boolean directed){
        this.n = data.length;
        this.data = data;
        this.directed = directed;
        matrix = new int[n][n];
    }
    /**
     *
     * @param v 起點
     * @param w 終點
     * @param value 權重
     */
    public void addEdge(int v , int w , int value){
        if((v >=0 && v < n) && (w >= 0 && w < n)){
            if(hasEdge(v,w) == value){
                return;
            }
            matrix[v][w] = value;
            if(!this.directed){
                matrix[w][v] = value;
            }
            n ++;
        }
    }


    //判斷兩個節點中是否以及存在邊
    public int hasEdge(int v, int w){
        if((v >=0 && v < n) && (w >= 0 && w < n)){
            return matrix[v][w];
        }
        return 0;
    }
    /**
     * 狀態轉移函數
     * @param index
     * @param value
     * @return
     */
    public int stateTransfer(int index , int value){
        int[] matrix = this.matrix[index];
        for (int i = 0; i < matrix.length; i++) {
            if(matrix[i] == value){
                return i;
            }
        }
????????return?Integer.MAX_VALUE;

2.鄰接表

如果圖是稀疏的，那么更好的解決辦法是使用鄰接表。

2.3圖的搜索算法

從圖的某個訂單出發，訪問途中的所有頂點，并且一個頂點只能被訪問一次。圖的搜索（遍歷）算法常見的有兩種，如下：

深度優先搜索算法（DFS）

廣度優先搜索算法（BFS）

03

數據結構與算法

3.1 BF（Brute Force）算法

3.1.1 算法介紹

BF（Brute Force）算法也可以叫暴力匹配算法或者樸素匹配算法。

3.1.2 算法過程

在講解算法之前，先定義兩個概念，方便后面講解。他們分別是主串（S）和模式串（P）。比如說要在字符串A中查找字符串B，那么A就是主串，B就是模式串。把主串的長度記作n，模式串的長度記作m，并且n>m。算法過程如下圖：

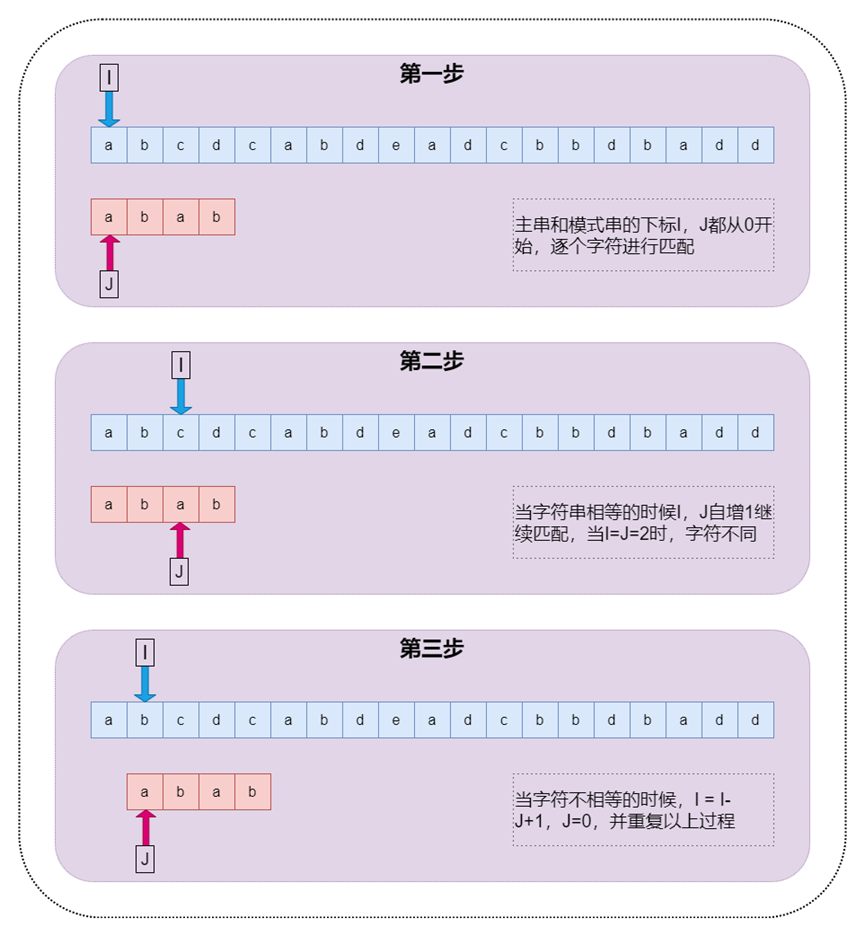
圖2 BF算法過程圖示

3.1.3 算法分析

BF算法過程很“暴力”，當然也就比較簡單，好懂，但是響應的性能也不高極端情況下時間復雜度函數為O(m*n)。

盡管理論上BF算法的時間復雜度很高，但在實際的開發中，它卻是一個比較常用的字符串匹配算法，主要原因有以下兩點：

樸素字符串匹配算法思想簡單，代碼實現也非常簡單，不容易出錯，容易調試和修改。

在實際的軟件開發中，模式串和主串的長度都不會太長，大部分情況下，算法執行的效率都不會太低。

3.2 RK（Rabin-Karp）算法

3.2.1算法介紹

RK算法全程叫Rabin-Karp算法，是有它的兩位發明者Rabin和Karp的名字來命名，這個算法理解并不難，它其實是BF算法的升級版。

3.2.2 算法過程

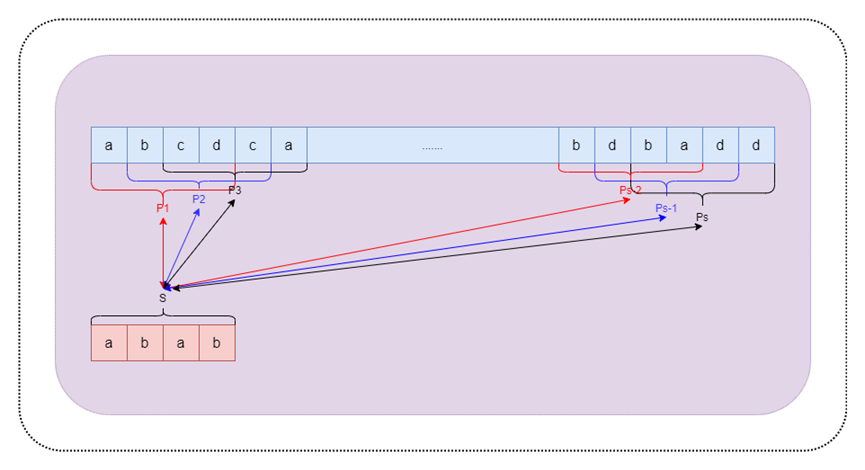
圖3 RK算法過程圖示

3.2.3算法分析

在BF算法中當字符串不匹配時，需要比對每一個字符，如果不能匹配則重新調整I，J的值重新比對每一個字符，RK的思路是將模式串進行哈希算法得到s=hash(P)，然后將主串分割成n-m+1個子串，分別對其進行hash算法，然后逐個和s進行比對，減少逐個字符串比對的次數。其中hash函數的具體實現可自行選擇。

整個RK算法包含兩部分：

計算模式串哈希和子串的哈希；

模式串哈希和子串哈希的比較；

第一部分的只需要掃描一遍主串就能計算出所有子串的哈希值，這部分的時間復雜度是O(n)。模式串哈希值與每個子串哈希之間的比較的時間復雜度是O(1)，總共需要比對n-m+1次，所以這部分的時間復雜度為O(n)。所以RK算法的整體時間復雜度為O(n)。

3.3KMP算法

3.3.1算法介紹

KMP算法是一種線性時間復雜度的字符串匹配算法，它是對BF(Brute-Force)算法的改進。KMP算法是由D.E.Knuth與V.R.Partt和J.H.Morris一起發現的，因此人們稱它為Knuth-Morris-Pratt算法，簡稱KMP算法。

前面介紹了BF算法，缺點就是時間消耗很大，KMP算法的主要思想就是：在匹配過程中發生匹配失敗時，并不是簡單的將模式串P的下標J重新置為0，而是根據一些匹配過程中得到的信息跳過不必要的匹配，從而達到一個較高的匹配效率。

3.3.2算法過程

在介紹KMP算法之前，首先介紹幾個字符串的概念：

前綴：不包含最后一個字符的所有以第一個字符開頭的連續子串；

后綴：不包含第一個字符的所有以最后一個字符結尾的連續子串；

最大公共前后綴：前綴集合與后綴集合中長度最大的子串；

例如字符串abcabc

前綴集合是a，ab，abc，abca，abcab

后綴集合為bcabc，cabc，abc，bc，c

最大公共前后綴為abc

KMP算法的過程如下圖：

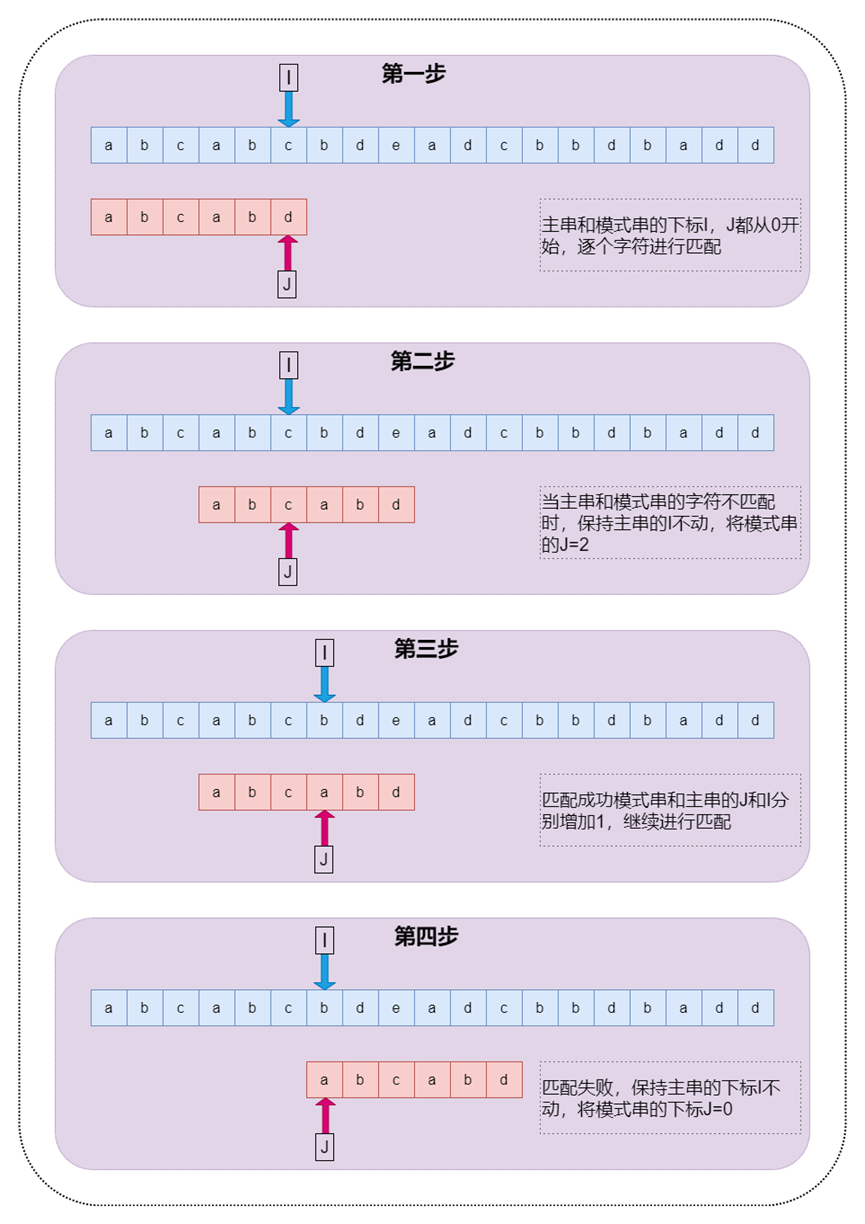
圖4 KMP算法過程圖示

那么為什么KMP算法會知道在匹配失敗時下標J回溯到那個位置呢？其實KMP算法在匹配的過程中將維護一些信息來幫助跳過不必要的匹配，這個信息就是KMP算法的重點，next數組也叫做fail數據或者前綴數據。下面來分析next數組的由來：

對于模式串P的每個元素P[j]，都存在一個實數k，使得模式串P開頭的k個字符(P[0]P[1]...P[k-1])依次于P[j]前面的k(P[j-k]P[j-k+1]...P[j-1])個字符相同。如果這樣的k有多個，則取最大的一個。模式串P中的每個位置j的字符都存在這樣的信息，采用next數組表示，即next[j]=MAX{k}。

從上述定義中可看到next(j)的邏輯意義就是求P[0]P[1]...P[j-1]的最大公共前后綴長度。代碼如下：

public static void genNext(Integer[] next , String p){
  int j = 0 , k = -1;
  char[] chars = p.toCharArray();
  next[0] = -1;
  while(j < p.length() - 1){
    if(k == -1 || chars[j] == chars[k]){
      j++;k++;
      next[j] = k;
    }else{
      k = next[k];//此處為理解難點
    }
  }
}

下面分析next的求解過程：

1. 特殊情況

當j的值為0或者1的時候，它們的k值都為0，即next(0) = 0 、next(1)= 0。為了后面k值計算的方便，我們將next(0)的值設置為-1。

2. 當P[j]==P[k]的情況

當P[j]==P[k]時，必然有P[0]...P[k-1]==P[j-k]...P[j-1]，因此有P[0]...P[k]==P[j-k]...P[j]，這樣就有next(j+1)=k+1。

3. 當P[j]!=P[k]的情況

當P[j]!=P[k]時，必然會有next(j)=k，并且next(j+1)

4. 算法優化

上述算法有一個小問題就是當P[k]匹配失敗后會跳轉到next(k)繼續進行匹配，但是此時有可能P[k]=P[next(k)]，此時匹配肯定是失敗的所以對上述代碼進行改進如下：

public void genNext(Integer[] next , String p){
  int j = 0 , k = -1;
  char[] chars = p.toCharArray();
  next[0] = -1;
  while(j < p.length() - 1){
    if(k == -1 || chars[j] == chars[k]){
      j++;k++;
      if(chars[j] == chars[k]){
        next[j] = next[k];//如果兩個相等
      }else{
        next[j] = k;
      }
    }else{
      k = next[k];
    }
  }
}

3.3.3算法分析

KMP算法通過消除主串指針的回溯提高匹配的效率，整個算法分為兩部分，next數據的求解，以及字符串匹配，從上一節的分析可知求解next數組的時間復雜度為O(m)，匹配算法的時間復雜度為O(n)，整體的時間復雜度為O(m+n)。KMP算法不是最快匹配算法，卻是名氣最大的，使用的范圍也非常廣。

3.4BM算法

3.4.1算法介紹

Boyer-Moore字符串搜索算法是一種非常高效的字符串搜索算法。它由BobBoyer和J Strother Moore發明，有實驗統計它的性能是KMP算法的3-4倍。

3.4.2算法過程

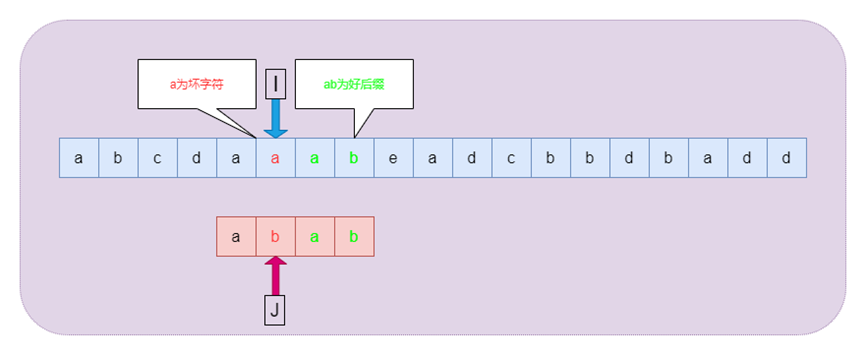
前面介紹的BF，KMP的算法的匹配過程雖然模式串的回溯過程不同，但是相同點都是從左往右逐個字符進行匹配，而BM算法則是采用的從右向左進行匹配，借助壞字符規則（SKip(j)）和好后綴規則（Shift(j)），能夠進行快速匹配。其中壞字符和好后綴示意如下圖

圖5壞字符和好后綴圖示

1. 壞字符規則：在BM算法從右向左掃描的過程中，若發現某個字符S[i]不匹配時，則按照如下兩種情況進行處理：

如果字符S[i]在模式串P中沒有出現，那么從字符S[i]開始的m個文本顯然是不可能和P匹配成功，直接全部跳過該區域。

如果字符S[i]在模式串P中出現，則以該字符進行對齊。

2. 好后綴規則：在BM算法中，若發現某個字符不匹配的同時，已有部分字符匹配成功，則按照如下兩種情況進行處理：

如果已經匹配的子串在模式串P中出現過，且子串的前一個字符和P[j]不相同，則將模式串移動到首次出現子串的前一個位置。

如果已經匹配的子串在模式串P中沒有出現過，則找到已經匹配的子串最大前綴，并移動模式串P到最大前綴的前一個字符。

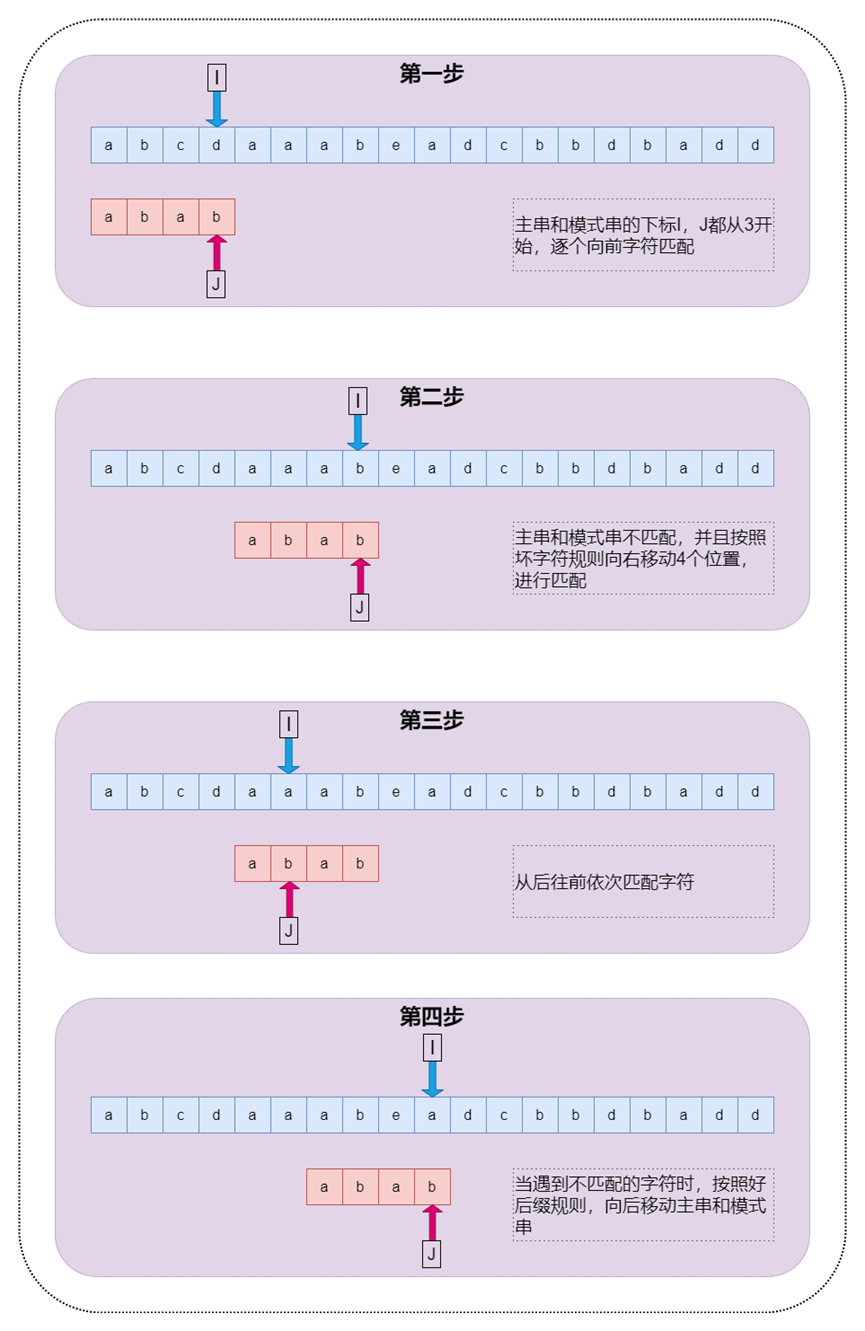
BM算法過程如下：

圖6BM算法過程圖示

3.4.3算法分析

在BM算法中，如果匹配失敗則取SKip(j)與Shift(j)中的較大者作為跳躍的距離。BM算法預處理階段的復雜度為O(m+n)，搜索階段的最好的時間復雜度為O(n/m)，最壞的時間復雜度為O(n*m)。由于BM算法采用的是后綴匹配算法，并且通過壞字符和好后綴共同作用下，可以跳過不必要的一些字符，具體Shift(j)的求解過程可參看KMP算法的next()函數過程。

3.5TireTree

3.5.1算法介紹

在搜索中常見數據結構與算法探究（一）中，介紹過一種樹狀的數據結構叫做HashTree，本章介紹的TireTree就是HashTree的一個變種。TireTree又叫做字典樹或者前綴樹，典型的應用是用于統計和排序大量的字符串，所以經常被搜索系統用于文本的統計或搜索。

TireTree的核心思想是空間換時間。TrieTree是一種高效的索引方法，它實際上是一種確定有限自動機(DFA)，利用字符串的公共前綴來降低查詢時間的開銷以達到提高查詢效率的目的，非常適合多模式匹配。TireTree有以下基本性質：

根節點不包含字符，除根節點外每個節點都包含一個字符。

從根節點到某一個節點，路徑上經過的字符連接起來，為該節點對應的字符串。

每個節點對應的所有子節點包含的字符都不相同。

3.5.2算法過程

TireTree構建與查詢

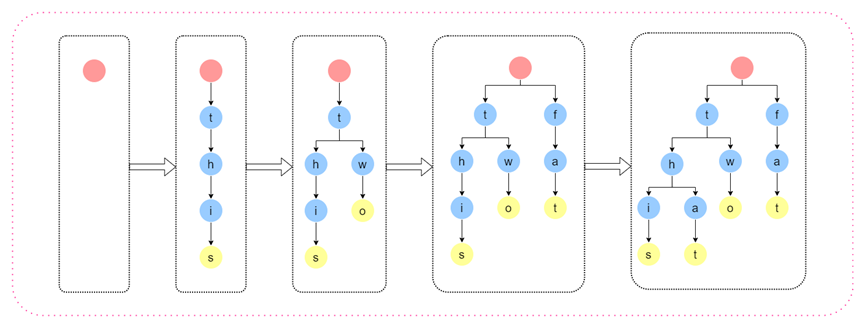
我們以《搜索中常見的數據結構與算法探究（一）》案例二中提到的字謎單詞為例，共包含this、two、fat和that四個單詞，我們來探究一下TireTree的構建過程如下圖：

圖7 TireTree算法過程圖示

上述過程描述了that，two，fat，that四個單詞的插入TireTree的過程，其中黃色的節點代表有單詞存在。由于TireTree的構建的過程是樹的遍歷，所以查詢過程和創建過程可以視為一個過程。

3.5.3算法分析

TireTree由于本身的特性非常適合前綴查找和普通查找，并且查詢的時間復雜度為O(log(n))，和hash比較在一些場景下性能要優于甚至取代hash，例如說前綴查詢（hash不支持前綴查詢）。

雖然TireTree的查詢速度會有一定的提升但是卻不支持后綴查詢，并且TireTree對空間利用率不高，且對中文的支持有限。

3.6 AC自動機

3.6.1算法介紹

AC自動機（Aho-Corasick automation）該算法在1975年產生于貝爾實驗室，是著名的多模匹配算法之一。要搞懂AC自動機，先得有TireTree和KMP模式匹配算法的基礎知識，上述章節有TireTree和KMP算法的詳細介紹。

3.6.2算法過程

AC自動機的構建過程需要如下步驟：

1. TireTree的構建，請參看TireTree章節

2. fail指針的構建

使當前字符失配時跳轉到具有最長公共前后綴的字符繼續匹配。如同 KMP算法一樣， AC自動機在匹配時如果當前字符匹配失敗，那么利用fail指針進行跳轉。由此可知如果跳轉，跳轉后的串的前綴，必為跳轉前的模式串的后綴并且跳轉的新位置的深度一定小于跳之前的節點。fail指針的求解過程可是完全參照KMP算法的next指針求解過程，此處不再贅述。

3. AC自動機查找

查找過程和TireTree相同，只是在查找失敗的時候感覺fail指針跳轉到指定的位置繼續進行匹配。

3.6.3算法分析

AC自動機利用fail指針阻止了模式串匹配階段的回溯，將時間復雜度優化到了O(n)。

3.7Double-Array-TireTree

3.7.1算法介紹

前面提到過TireTree雖然很完美，但是空間利用率很低，雖然可以通過動態分配數組來解決這個問題。為了解決這個問題引入Double-Array-TireTree，顧名思義Double-Array-TireTree就是TireTree壓縮到兩個一維數組BASE和CHECK來表示整個樹。Double-Array-TireTree擁有TireTree的所有優點，而且克服了TireTree浪費空間的不足，使其應用范圍更加廣泛，例如詞法分析器，圖書搜索，拼寫檢查，常用單詞過濾器，自然語言處理中的字典構建等等。

3.7.2算法過程

在介紹算法之前，提前簡單介紹一個概念DFA（下一篇詳細介紹）。DFA（DeterministicFinite State）有限自動機，通俗來講DFA是指給定一個狀態和一個輸入變量，它能轉到的下一個狀態也就確定下來，同時狀態是有限的。

Double-Array-TireTree構建

Double-Array-TireTree終究是一個樹結構，樹結構的兩個重要的要素便是前驅和后繼，把樹壓縮在雙數組中，只需要保持能查到每個節點的前驅和后繼。首先要介紹幾個重要的概念：

STATE：狀態，實際是在數組中的下標

CODE：狀態轉移值，實際為轉移字符的值

BASE：標識后繼節點的基地址數組

CHECK：標識前驅節點的地址

從上面的概念的可以理解如下規則，假設一個輸入的字符為c，狀態從s轉移到t

state[t] = base[state[s]] + code[c]

check[state[t]] = state[s]

構建的過程大概也分為兩種：

動態輸入詞語，動態構建雙數組

已知所有詞語，靜態構建雙數組

以靜態構建過為核心，以《搜索中常見的數據結構與算法探究（一）》案例二中提到的字謎單詞為例，共包含this、two、fat和that四個單詞為例，其中涉及到的字符集{a,f,h,i,o,s,t,w}共8個字符，為了后續描述方便，對這個八個字符進行編碼，分別是a-1,f-2,h-3,i-4,o-5,s-6,t-7,w-8

構建this，如下圖

圖8 構建This圖示

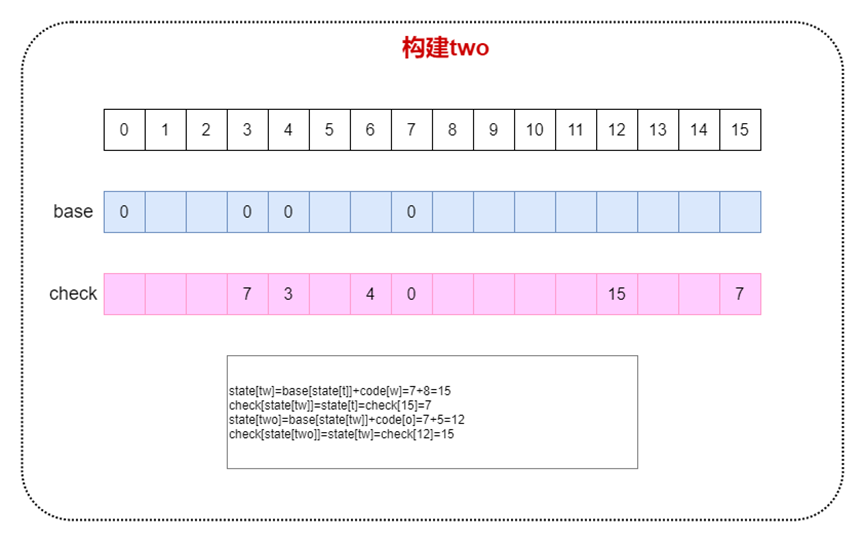
構建two，如下圖

圖9構建two圖示

構建fat，如下圖

圖10構建fat圖示

構建that，如下圖

圖11 構建that圖示

Double-Array-TireTree查詢

驗證this是否在范圍內如下過程

1. state[t]= base[state[null]]+code[t]= 0 + 7=7

check[7]=state[null]=0 通過

2. state[th]= base[state[t]]+code[h]=base[7]+3 =2+3=5

check[5]= state[t] = 7 通過

3. state[tha]= base[state[th]]+ code[a]=base[5]+1=5+1=6

check[6]=state[th]=5 通過

4. state[that]= base[state[tha]]+t = base[6]+7=11

check[11]=state[tha]=6 通過

3.7.3算法分析

通過兩個數據base和check將TireTree的數據壓縮到兩個數組中，既保留了TireTree的搜索的高效，又充分利用了存儲空間。

3.8其他數據結構

鑒于篇幅有限，DFA，FSA以及FST將在下一篇文章中再來一起討論，敬請期待！

04

總結

本篇文章對本系列的上一篇文章的常見數據結構做了補充，介紹了非線性數據結構的最后一種，圖數據結構作為基本數據結構最復雜的一種，在多種企業級應用中都有使用，如網絡拓撲，流程引擎，流程編排；另外本文重點介紹了幾種常見的匹配算法，以及算法的演進過程和使用場景，為下一篇的主題，也是本系列的重點探究的目標，“搜索”做一個鋪墊，敬請期待！

審核編輯：劉清