一
后摩爾時代我們所遇到的瓶頸 后摩爾時代,IC技術瓶頸主要有如圖 1-1所示的四點。其中,IC瓶頸之一、之二和之四均取決于高效準確的電磁設計。

圖1-1 后摩爾時代IC技術瓶頸 傳統的基于準靜態的寄生參數提取算法,由于無法處理趨膚效應,無法捕捉互連線的頻變效應,無法捕捉電場-磁場耦合效應(如圖 1-2),所以其仿真精度不夠,需要使用全波電磁仿真方法。
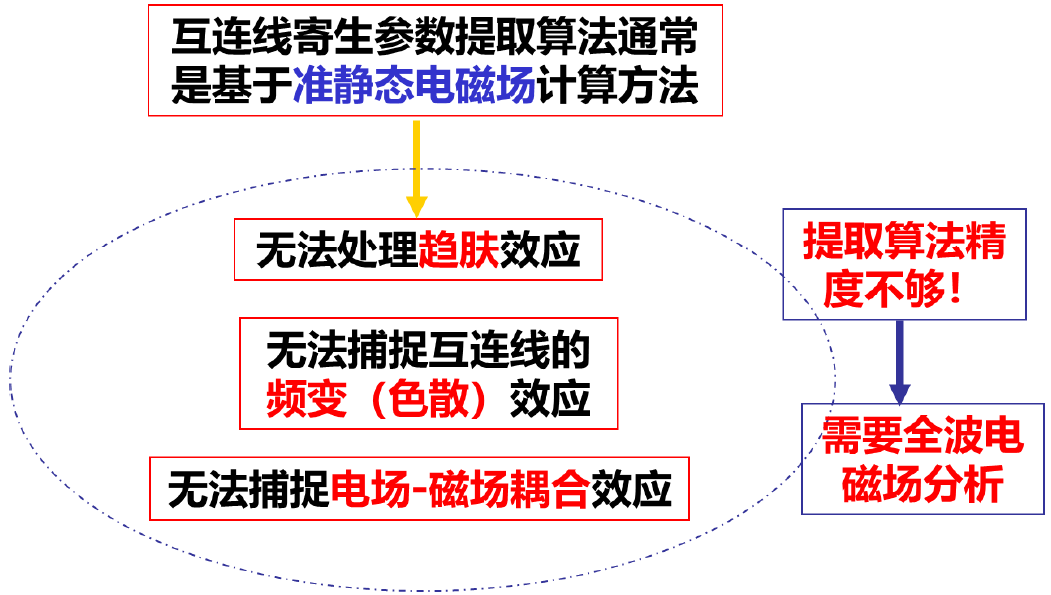
圖1-2 準靜態電磁計算的不足
二
常見全波電磁仿真方法介紹與比較
全波電磁仿真方法很多,圖 2-1做了一個歸類。在眾多方法中,有限元(Finite Element Method, FEM)和矩量法(Method of Moment, MoM)是最有代表性的兩種方法。FEM基于麥克斯韋方程的微分形式,該方法使用體剖分進行空間的全域離散,所以會產生較多的剖分單元。而MoM方法基于麥克斯韋方程的積分形式,可以使用面剖分或體剖分進行目標物體的離散,其生成的剖分個數遠小于FEM。
圖 2-2給出了體和面剖分基本單位形狀。
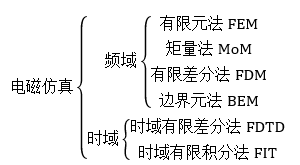
圖 2-1 電磁仿真方法

圖 2-2 剖分基本單元形狀
圖 2-3給出了不同算法的應用場景。傳統的MoM和FEM方法由于計算效率問題,都只適用于較小規模的電磁問題。雖然MoM生成的未知數個數會遠小于FEM,但是,MoM生成的矩陣是一個稠密矩陣,其直接求解的計算復雜度為O(N3),即使使用迭代求解,每一次迭代其計算復雜度依然高達O(N2)。所以,一般可以采用基于MoM的快速算法減小計算復雜度,加速求解過程,并擴大求解規模。如果問題進一步擴大,則只能使用一些近似算法,如物理光學(Physical Optics, PO)或幾何光學(Geometric Optics, GO)進行近似計算,這些方法主要用于超大電尺寸的物體散射問題。
進一步把問題聚焦于芯片的電磁仿真領域,雖然FEM、MoM及時域有限差分法(Finite Difference Time Domain, FDTD)等計算電磁方法都能用于芯片仿真。但是相對于基于微分方程的FEM和FDTD,目前專用的芯片電磁仿真軟件基本都基于積分方程MoM法,比如Cadence和Keysight的芯片版圖專用電磁仿真工具。雖然一些通用的電磁仿真軟件(比如基于FEM的通用仿真軟件)也能用于芯片電磁仿真,但是通用電磁仿真軟件與芯片設計軟件沒有很好的交互,且基于FEM的軟件需要施加邊界條件,增加了使用的復雜度。更重要的,對于介質金屬層層堆疊的芯片結構,FEM、FDTD等基于偏微分方程的數值算法需要對多層介質環境進行剖分,導致求解未知數巨大;而MoM可以把介質效應放到平面分層格林函數(Layered Medium Green’s Function)中,這樣只需要對金屬層進行表面網格剖分,相比FEM、FDTD等算法,MoM可以大大減少了求解未知數。
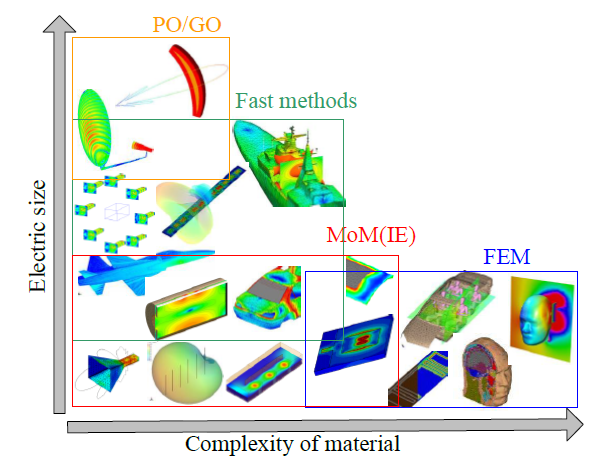
圖 2-3 幾種算法的應用范圍
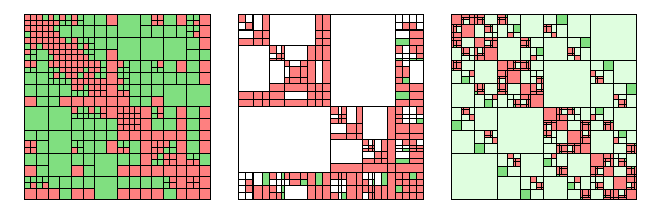
圖 2-4 H-矩陣算法(綠色表示滿足H-Matrix 稀疏化存儲的矩陣單元)
然而對于大規模芯片問題,即使使用平面分層格林函數,MoM 生成的稠密矩陣方程的求解依然非常慢。隨著多種快速低秩分解方法的提出,快速直接求解(Fast DirectSolver)方法在電磁計算領域得到了很大發展。利用相互分離的基函數組之間的低秩特性,直接求解方法將系統矩陣分割壓縮成多層稀疏化表示形式。多層自適應交叉近似(Adaptive Cross Approximation Algorithm, ACA)矩陣分解算法、H 矩陣法(如圖 2-4 示)和多層UV 方法等都是基于矩陣壓縮的算法,但是直接對矩陣進行操作,壓縮程度跟矩陣狀態相關。另外,雖然直接法近些年發展很快,但是直接法的計算規模尚遠不足以比擬快速迭代算法,且面向復雜工程需求,仍有很多亟待解決的挑戰。
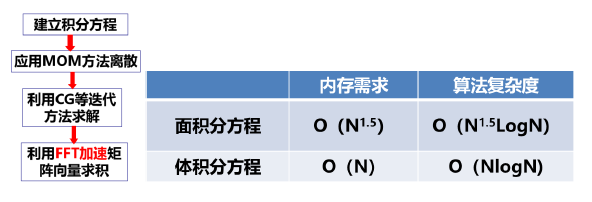
圖 2-5 基于FFT的算法
使用快速迭代求解,是解決MoM稠密矩陣方程求解的另一種有效路徑。比如基于快速傅里葉變換(FFT)的方法,如圖 2-5所示。但是,對于面積分方程求解,為了實現FFT算法,該方法需要增加許多補零,導致效率降低。三

圖 3-1 20世紀最偉大的十大算法
快速多極子(Fast Multipole Method, FMM)作為20世紀最偉大的十大算法(如圖 3-1所示)之一被用于包含電磁計算在內的多種應用中。該方法而后進一步被拓展成更高效的多層快速多極子(Multi-level Fast Multipole Algorithm, MLFMA),它將整個場分為近場區和遠場區重新組合加速矩陣-向量乘法,并將迭代方法的計算復雜度降低為O(NlogN),極大地提高了仿真效率,擴大了仿真規模(如圖 3-2所示)。
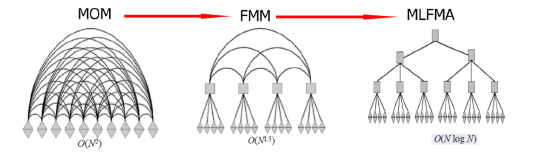
圖 3-2 從矩量法發展到多層快速多極子算法計算復雜度的變化
法動科技作為射頻EDA行業的領先者,自主開發了一種新的MLFMA用于芯片的電磁仿真,該方法可以同時適用于平面分層格林函數這類復雜的核函數。即使使用平面分層格林函數來減少未知數的情況下,依然可以得到O(NlogN)的計算復雜度,極大地提升芯片電磁仿真的效率。
法動科技: 成立于2017年。作為擁有硅谷及斯坦福創新基因的國際一流團隊,我們專業提供射頻微波電子設計自動化(EDA)軟件,憑借自主研發的大容量、快速三維全波電磁仿真引擎和基于人工智能技術的高效系統級仿真引擎,能夠在射頻微波芯片、封裝、高速PCB等領域為用戶提供快速準確的電磁仿真、建模及優化設計方案。 同時,我們可以為包括移動通信、物聯網、5G、雷達、衛星通信系統和高速數字設計在內的產品提供高水平設計開發服務。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4601瀏覽量
92673 -
仿真
+關注
關注
50文章
4048瀏覽量
133431 -
電磁
+關注
關注
15文章
1075瀏覽量
51726
原文標題:芯片電磁仿真算法介紹
文章出處:【微信號:FaradayDynamics,微信公眾號:法動科技】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 常見全波電磁仿真方法介紹與比較
常見全波電磁仿真方法介紹與比較










評論