沒事兒的時候我喜歡玩玩那些經(jīng)典的 2D 網(wǎng)頁小游戲，我發(fā)現(xiàn)很多游戲都要涉及地圖的隨機生成，比如掃雷游戲中地雷的位置應(yīng)該是隨機分布的：

再比如經(jīng)典炸彈人游戲，障礙物的位置也是有一定隨機性的：

這些 2D 游戲相較現(xiàn)在的大型 3D 游戲雖然看起來有些簡陋，但依然用到很多有趣算法技巧，本文就來深入研究一下地圖的隨機生成算法。

2D 游戲的地圖肯定可以抽象成一個二維矩陣，就拿掃雷舉例吧，我們可以用下面這個類表示掃雷的棋盤：

classGame{
intm,n;
//大小為m*n的二維棋盤
//值為true的地方代表有雷，false代表沒有雷
boolean[][]board;
}

如果你想在棋盤中隨機生成k個地雷，也就是說你需要在board中生成k個不同的(x, y)坐標，且這里面x, y都是隨機生成的。

對于這個需求，首先一個優(yōu)化就是對二維矩陣進行「降維打擊」，把二維數(shù)組轉(zhuǎn)化成一維數(shù)組：

classGame{
intm,n;
//長度為m*n的一維棋盤
//值為true的地方代表有雷，false代表沒有雷
boolean[]board;

//將二維數(shù)組中的坐標(x,y)轉(zhuǎn)化為一維數(shù)組中的索引
intencode(intx,inty){
returnx*n+y;
}

//將一維數(shù)組中的索引轉(zhuǎn)化為二維數(shù)組中的坐標(x,y)
int[]decode(intindex){
returnnewint[]{index/n,index%n};
}
}

這樣，我們只要在[0, m * n)中選取一個隨機數(shù)，就相當(dāng)于在二維數(shù)組中隨機選取了一個元素。

但問題是，我們現(xiàn)在需要隨機選出k個不同的位置放地雷。你可能說，那在[0, m * n)中選出來k個隨機數(shù)不就行了？

是的，但實際操作起來有些麻煩，因為你很難保證隨機數(shù)不重復(fù)。如果出現(xiàn)重復(fù)的隨機數(shù)，你就得再隨機選一次，直到找到k個不同的隨機數(shù)。

如果k比較小m * n比較大，那出現(xiàn)重復(fù)隨機數(shù)的概率還比較低，但如果k和m * n的大小接近，那么出現(xiàn)重復(fù)隨機數(shù)的概率非常高，算法的效率就會大幅下降。

那么，我們有沒有更好的辦法能夠在線性的時間復(fù)雜度解決這個問題？其實是有的，而且有很多種解決方案。

洗牌算法

第一個解決方案，我們可以換個思路，避開「在數(shù)組中隨機選擇k個元素」這個問題，把問題轉(zhuǎn)化成「如何隨機打亂一個數(shù)組」。

現(xiàn)在想隨機初始化k顆地雷的位置，你可以先把這k顆地雷放在board開頭，然后把board數(shù)組隨機打亂，這樣地雷不就隨機分布到board數(shù)組的各個地方了嗎？

洗牌算法，或者叫隨機亂置算法就是專門解決這個問題的，我們可以看下力扣第 384 題「打亂數(shù)組」：

這個shuffle函數(shù)是算法的關(guān)鍵，直接看解法代碼吧：

classSolution{
privateint[]nums;
privateRandomrand=newRandom();

publicSolution(int[]nums){
this.nums=nums;
}

publicint[]reset(){
returnnums;
}

//洗牌算法
publicint[]shuffle(){
intn=nums.length;
int[]copy=Arrays.copyOf(nums,n);
for(inti=0;i//生成一個[i,n-1]區(qū)間內(nèi)的隨機數(shù)
intr=i+rand.nextInt(n-i);
//交換nums[i]和nums[r]
swap(copy,i,r);
}
returncopy;
}

privatevoidswap(int[]nums,inti,intj){
inttemp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
}

洗牌算法的時間復(fù)雜度是 O(N)，而且邏輯很簡單，關(guān)鍵在于讓你證明為什么這樣做是正確的。排序算法的結(jié)果是唯一可以很容易檢驗的，但隨機亂置算法不一樣，亂可以有很多種，你怎么能證明你的算法是「真的亂」呢？

分析洗牌算法正確性的準則：產(chǎn)生的結(jié)果必須有n!種可能。這個很好解釋，因為一個長度為n的數(shù)組的全排列就有n!種，也就是說打亂結(jié)果總共有n!種。算法必須能夠反映這個事實，才是正確的。

有了這個原則再看代碼應(yīng)該就容易理解了：

對于nums[0]，我們把它隨機換到了索引[0, n)上，共有n種可能性；

對于nums[1]，我們把它隨機換到了索引[1, n)上，共有n - 1種可能性；

對于nums[2]，我們把它隨機換到了索引[2, n)上，共有n - 2種可能性；

以此類推，該算法可以生成n!種可能的結(jié)果，所以這個算法是正確的，能夠保證隨機性。

水塘抽樣算法

學(xué)會了洗牌算法，掃雷游戲的地雷隨機初始化問題就解決了。不過別忘了，洗牌算法只是一個取巧方案，我們還是得面對「在若干元素中隨機選擇k個元素」這個終極問題。

要知道洗牌算法能夠生效的前提是你使用數(shù)組這種數(shù)據(jù)結(jié)構(gòu)，如果讓你在一條鏈表中隨機選擇k個元素，肯定不能再用洗牌算法來蒙混過關(guān)了。

再比如，假設(shè)我們的掃雷游戲中棋盤的長和寬非常大，已經(jīng)不能在內(nèi)存中裝下一個大小為m * n的board數(shù)組了，我們只能維護一個大小為k的數(shù)組記錄地雷的位置：

classGame{
//棋盤的行數(shù)和列數(shù)（非常大）
intm,n;
//長度為k的數(shù)組，記錄k個地雷的一維索引
int[]mines;

//將二維數(shù)組中的坐標(x,y)轉(zhuǎn)化為一維數(shù)組中的索引
intencode(intx,inty){
returnx*n+y;
}

//將一維數(shù)組中的索引轉(zhuǎn)化為二維數(shù)組中的坐標(x,y)
int[]decode(intindex){
returnnewint[]{index/n,index%n};
}
}

這樣的話，我們必須想辦法在[0, m*n)中隨機選取k個不同的數(shù)字了。

這就是常見的隨機抽樣場景，常用的解法是水塘抽樣算法（Reservoir Sampling）。水塘抽樣算法是一種隨機概率算法，會者不難，難者不會。

我第一次見到這個算法問題是谷歌的一道算法題：給你一個未知長度的單鏈表，請你設(shè)計一個算法，只能遍歷一次，隨機地返回鏈表中的一個節(jié)點。

這里說的隨機是均勻隨機（uniform random），也就是說，如果有n個元素，每個元素被選中的概率都是1/n，不可以有統(tǒng)計意義上的偏差。

一般的想法就是，我先遍歷一遍鏈表，得到鏈表的總長度n，再生成一個[0,n-1)之間的隨機數(shù)為索引，然后找到索引對應(yīng)的節(jié)點。但這不符合只能遍歷一次鏈表的要求。

這個問題的難點在于隨機選擇是「動態(tài)」的，比如說你現(xiàn)在你已經(jīng)遍歷了 5 個元素，你已經(jīng)隨機選取了其中的某個元素a作為結(jié)果，但是現(xiàn)在再給你一個新元素b，你應(yīng)該留著a還是將b作為結(jié)果呢？以什么邏輯做出的選擇，才能保證你的選擇方法在概率上是公平的呢？

先說結(jié)論，當(dāng)你遇到第i個元素時，應(yīng)該有1/i的概率選擇該元素，1 - 1/i的概率保持原有的選擇。看代碼容易理解這個思路：

/*返回鏈表中一個隨機節(jié)點的值*/
intgetRandom(ListNodehead){
Randomr=newRandom();
inti=0,res=0;
ListNodep=head;
//while循環(huán)遍歷鏈表
while(p!=null){
i++;
//生成一個[0,i)之間的整數(shù)
//這個整數(shù)等于0的概率就是1/i
if(0==r.nextInt(i)){
res=p.val;
}
p=p.next;
}
returnres;
}

對于概率算法，代碼往往都是很淺顯的，但是這種問題的關(guān)鍵在于證明，你的算法為什么是對的？為什么每次以1/i的概率更新結(jié)果就可以保證結(jié)果是平均隨機的？

我們來證明一下，假設(shè)總共有n個元素，我們要的隨機性無非就是每個元素被選擇的概率都是1/n對吧，那么對于第i個元素，它被選擇的概率就是：

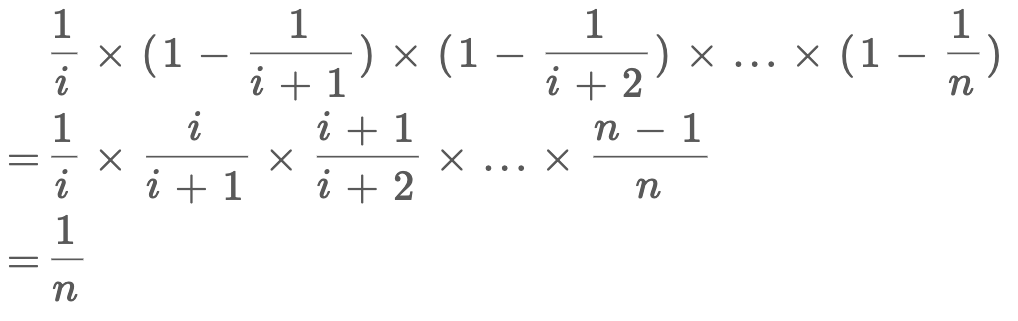
第i個元素被選擇的概率是1/i，在第i+1次不被替換的概率是1 - 1/(i+1)，在第i+2次不被替換的概率是1 - 1/(i+2)，以此類推，相乘的結(jié)果是第i個元素最終被選中的概率，也就是1/n。因此，該算法的邏輯是正確的。

同理，如果要在單鏈表中隨機選擇k個數(shù)，只要在第i個元素處以k/i的概率選擇該元素，以1 - k/i的概率保持原有選擇即可。代碼如下：

/*返回鏈表中k個隨機節(jié)點的值*/
int[]getRandom(ListNodehead,intk){
Randomr=newRandom();
int[]res=newint[k];
ListNodep=head;

//前k個元素先默認選上
for(inti=0;inull;i++){
res[i]=p.val;
p=p.next;
}

inti=k;
//while循環(huán)遍歷鏈表
while(p!=null){
i++;
//生成一個[0,i)之間的整數(shù)
intj=r.nextInt(i);
//這個整數(shù)小于k的概率就是k/i
if(jreturnres;
}

對于數(shù)學(xué)證明，和上面區(qū)別不大：

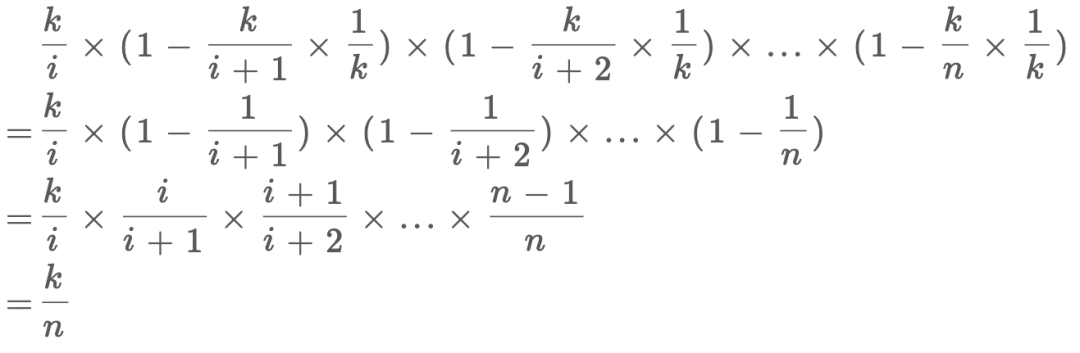
雖然每次更新選擇的概率增大了k倍，但是選到具體第i個元素的概率還是要乘1/k，也就回到了上一個推導(dǎo)。

類似的，回到掃雷游戲的隨機初始化問題，我們可以寫一個這樣的sample抽樣函數(shù)：

//在區(qū)間[lo,hi)中隨機抽取k個數(shù)字
int[]sample(intlo,inthi,intk){
Randomr=newRandom();
int[]res=newint[k];

//前k個元素先默認選上
for(inti=0;iinti=k;
//while循環(huán)遍歷數(shù)字區(qū)間
while(i//生成一個[0,i)之間的整數(shù)
intj=r.nextInt(i);
//這個整數(shù)小于k的概率就是k/i
if(j1;
}
}
returnres;
}

這個函數(shù)能夠在一定的區(qū)間內(nèi)隨機選擇k個數(shù)字，確保抽樣結(jié)果是均勻隨機的且只需要 O(N) 的時間復(fù)雜度。

蒙特卡洛驗證法

上面講到的洗牌算法和水塘抽樣算法都屬于隨機概率算法，雖然從數(shù)學(xué)上推導(dǎo)上可以證明算法的思路是正確的，但如果你筆誤寫出 bug，就會導(dǎo)致概率上的不均等。更神奇的是，力扣的判題機制能夠檢測出這種概率錯誤。

那么最后我就來介紹一種方法檢測隨機算法的正確性：蒙特卡洛方法。我猜測力扣的判題系統(tǒng)也是利用這個方法來判斷隨機算法的正確性的。

記得高中有道數(shù)學(xué)題：往一個正方形里面隨機打點，這個正方形里緊貼著一個圓，告訴你打點的總數(shù)和落在圓里的點的數(shù)量，讓你計算圓周率。

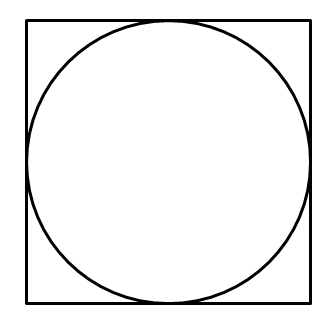
這其實就是利用了蒙特卡羅方法：當(dāng)打的點足夠多的時候，點的數(shù)量就可以近似代表圖形的面積。結(jié)合面積公式，可以很容易通過正方形和圓中點的數(shù)量比值推出圓周率的。

當(dāng)然，打的點越多，算出的圓周率越準確，充分體現(xiàn)了大力出奇跡的道理。

比如，我們可以這樣檢驗水塘抽樣算法sample函數(shù)的正確性：

publicstaticvoidmain(String[]args){
//在[12,22)中隨機選3個數(shù)
intlo=12,hi=22,k=3;
//記錄每個元素被選中的次數(shù)
int[]count=newint[hi-lo];
//重復(fù)10萬次
intN=1000000;
for(inti=0;iint[]res=sample(lo,hi,k);
for(intelem:res){
//對隨機選取的元素進行記錄
count[elem-lo]++;
}
}
System.out.println(Arrays.toString(count));
}

這段代碼的輸出如下：

[300821,299598,299792,299198,299510,300789,300022,300326,299362,300582]

當(dāng)然你可以做更細致的檢查，不過粗略看看，各個元素被選中的次數(shù)大致是相同的，這個算法實現(xiàn)的應(yīng)該沒啥問題。

對于洗牌算法中的shuffle函數(shù)也可以采取類似的驗證方法，我們可以跟蹤某一個元素x被打亂后的索引位置，如果x落在各個索引的次數(shù)基本相同，則說明算法正確，你可以自己嘗試實現(xiàn)，我就不貼代碼驗證了。

拓展延伸

到這里，常見的隨機算法就講完了，簡單總結(jié)下吧。

洗牌算法主要用于打亂數(shù)組，比如我們在快速排序詳解及運用中就用到了洗牌算法保證快速排序的效率。

水塘抽樣算法的運用更加廣泛，可以在序列中隨機選擇若干元素，且能保證每個元素被選中的概率均等。

對于這些隨機概率算法，我們可以用蒙特卡洛方法檢驗其正確性。

最后留幾個拓展題目：

1、本文開頭講到了將二維數(shù)組坐標(x, y)轉(zhuǎn)化成一維數(shù)組索引的技巧，那么你是否有辦法把三維坐標(x, y, z)轉(zhuǎn)化成一維數(shù)組的索引呢？

2、如何對帶有權(quán)重的樣本進行加權(quán)隨機抽取？比如給你一個數(shù)組w，每個元素w[i]代表權(quán)重，請你寫一個算法，按照權(quán)重隨機抽取索引。比如w = [1,99]，算法抽到索引 0 的概率是 1%，抽到索引 1 的概率是 99%，答案見我的這篇文章。

3、實現(xiàn)一個生成器類，構(gòu)造函數(shù)傳入一個很長的數(shù)組，請你實現(xiàn)randomGet方法，每次調(diào)用隨機返回數(shù)組中的一個元素，多次調(diào)用不能重復(fù)返回相同索引的元素。要求不能對該數(shù)組進行任何形式的修改，且操作的時間復(fù)雜度是 O(1)，答案見我的這篇文章