什么是堆
堆(heap),是一類特殊的數(shù)據(jù)結(jié)構(gòu)的統(tǒng)稱。它通常被看作一棵樹的數(shù)組對(duì)象。在隊(duì)列中,調(diào)度程序反復(fù)提取隊(duì)列中的第一個(gè)作業(yè)并運(yùn)行,因?yàn)閷?shí)際情況中某些時(shí)間較短的任務(wù)卻可能需要等待很長(zhǎng)時(shí)間才能開始執(zhí)行,或者某些不短小、但很重要的作業(yè),同樣應(yīng)當(dāng)擁有優(yōu)先權(quán)。而堆就是為了解決此類問題而設(shè)計(jì)的數(shù)據(jù)結(jié)構(gòu)。
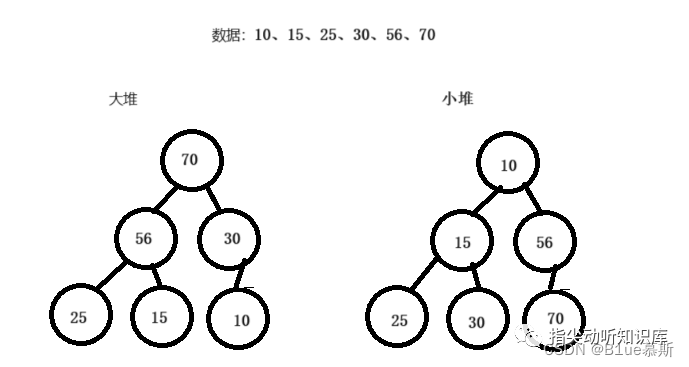
二叉堆是一種特殊的堆,二叉堆是完全二叉樹或者近似完全二叉樹,二叉堆滿足堆特性:父節(jié)點(diǎn)的鍵值總是保持固定的序關(guān)系于任何一個(gè)子節(jié)點(diǎn)的鍵值,且每個(gè)節(jié)點(diǎn)的左子樹和右子樹都是一個(gè)二叉堆。
當(dāng)父節(jié)點(diǎn)的鍵值總是大于任何一個(gè)子節(jié)點(diǎn)的鍵值時(shí)為最大堆,當(dāng)父節(jié)點(diǎn)的鍵值總是小于或等于任何一個(gè)子節(jié)點(diǎn)的鍵值時(shí)為最小堆。
為了更加形象,我們常用帶數(shù)字的圓圈和線條來表示二叉堆等,但其實(shí)都是用數(shù)組來表示的。如果根節(jié)點(diǎn)在數(shù)組中的位置是1,第n個(gè)位置的子節(jié)點(diǎn)則分別在2n和2n+1位置上。
如下圖所描的,第2個(gè)位置的子節(jié)點(diǎn)在4和5,第4個(gè)位置的子節(jié)點(diǎn)在8和9。所以我們獲得父節(jié)點(diǎn)和子節(jié)點(diǎn)的方式如下:
PARENT(i)
1 return 小于或等于i/2的最大整數(shù)
LEFT-CHILD(i)
1 return 2i
RIGHT-CHILD(i)
1 return 2i+1
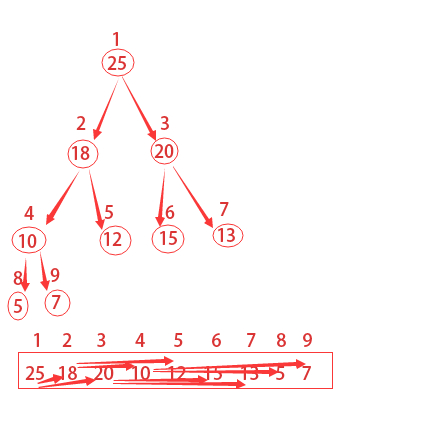
假定表示堆的數(shù)組為A,那么A.length通常給出數(shù)組元素的個(gè)數(shù),A.heap?size表示有多少個(gè)堆元素存儲(chǔ)在該數(shù)組中。這句話略帶拗口,也就是說數(shù)組A[1...A.length]可能都有數(shù)據(jù)存放,但只有A[1...A.heap?size]中存放的數(shù)據(jù)才是堆中的有效數(shù)據(jù)。毫無疑問0≤A.heap?size≤A.length。
最大堆除了根以外所有結(jié)點(diǎn)i都滿足:A[PARENT(i)]≥A[i]。
最小堆除了根以外所有結(jié)點(diǎn)i都滿足:A[PARENT(i)]≤A[i]。
一個(gè)堆中結(jié)點(diǎn)的高度是該結(jié)點(diǎn)到葉借點(diǎn)最長(zhǎng)簡(jiǎn)單路徑上邊的數(shù)目,如上圖所示編號(hào)為4的結(jié)點(diǎn)的高度為1,編號(hào)為2的結(jié)點(diǎn)的高度為2,樹的高度就是3。
包含n個(gè)元素的隊(duì)可以看作一顆完全二叉樹,那么該堆的高度是Θ(lgn)。
通過MAX-HEAPIFY維護(hù)最大堆
程序中,不可能所有的堆都天生就是最大堆,為了更好的使用堆這一數(shù)據(jù)結(jié)構(gòu),我們可能要人為地構(gòu)造最大堆。
如何將一個(gè)雜亂排序的堆重新構(gòu)造成最大堆,它的主要思路是:
從上往下,將父節(jié)點(diǎn)與子節(jié)點(diǎn)以此比較。如果父節(jié)點(diǎn)最大則進(jìn)行下一步循環(huán),如果子節(jié)點(diǎn)更大,則將子節(jié)點(diǎn)與父節(jié)點(diǎn)位置互換,并進(jìn)行下一步循環(huán)。注意父節(jié)點(diǎn)要與兩個(gè)子節(jié)點(diǎn)都進(jìn)行比較。
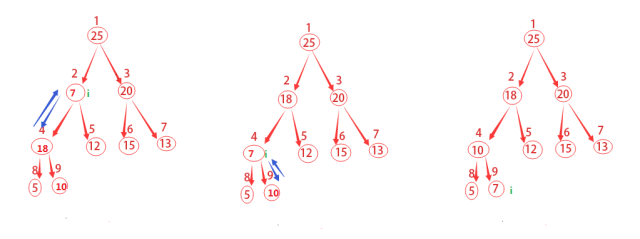
如上圖說描述的,這里從結(jié)點(diǎn)為2開始做運(yùn)算。先去l為4,r為5,將其與父節(jié)點(diǎn)做比較,發(fā)現(xiàn)左子節(jié)點(diǎn)比父節(jié)點(diǎn)更大。因此將它們做交換,設(shè)4為最大的結(jié)點(diǎn),并繼續(xù)以結(jié)點(diǎn)4開始做下一步運(yùn)算。
因此可以給出偽代碼如下:
MAX-HEAPIFY(A,i)
1 l=LEFT-CHILD(i)
2 r=RIGHT-CHILD(i)
3 if l<=A.heap-size and A[l]>A[i]
4 largest=l
5 else
6 largest=i
7 if r<=A.heap-size and A[r]>A[largest]
8 largest=r
9 if largest != i
10 exchange A[i] with A[largest]
11 MAX-HEAPIFY(A,largest)
在以上這些步驟中,調(diào)整A[i]、A[l]、A[r]的關(guān)系的時(shí)間代價(jià)為Θ(1),再加上一棵以i的子節(jié)點(diǎn)為根結(jié)點(diǎn)的子樹上運(yùn)行MAX-HEAPIFY的時(shí)間代價(jià)(注意此處的遞歸不一定會(huì)發(fā)生,此處只是假設(shè)其發(fā)生)。因?yàn)槊總€(gè)子節(jié)點(diǎn)的子樹的大小至多為2n/3(最壞情況發(fā)生在樹的底層恰好半滿的時(shí)候)。因此MAX-HEAPIFY過程的運(yùn)行時(shí)間為:
T(n)≤T(2n/3)+Θ(1)
也就是:
T(n)=O(lgn)
通過BUILD-MAX-HEAP構(gòu)建最大堆
前面我們通過自頂向下的方式維護(hù)了一個(gè)最大堆,這里將通過自底向上的方式通過MAX-HEAPIFY將一個(gè)n=A.length的數(shù)組A[1...n]轉(zhuǎn)換成最大堆。
回顧一下上面的圖示,其總共有9個(gè)結(jié)點(diǎn),取小于或等于9/2的最大整數(shù)為4,從4+1,4+2,一直到n都是該樹的葉子結(jié)點(diǎn),你發(fā)現(xiàn)了么?這對(duì)任意n都是成立的哦。
因此這里我們就要從4開始不斷的調(diào)用MAX-HEAPIFY(A,i)來構(gòu)建最大堆。
為什么會(huì)有這一思路呢?
原因是既然我們知道了哪些結(jié)點(diǎn)是葉子結(jié)點(diǎn),從最后一個(gè)非葉子結(jié)點(diǎn)(這里是4)開始,一次調(diào)用MAX-HEAPIFY函數(shù),就會(huì)將該結(jié)點(diǎn)與葉子結(jié)點(diǎn)做相應(yīng)的調(diào)整,這其實(shí)也就是一個(gè)遞歸的過程。
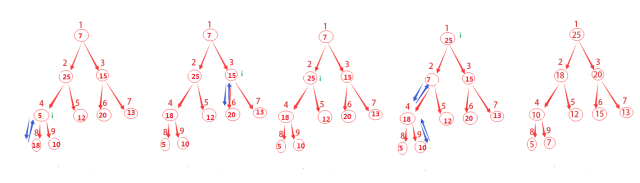
圖示已經(jīng)這么清晰了,就直接上偽代碼咯。
BUILD-MAX-HEAP(A)
1 A.heap-size=A.length
2 for i=小于或等于A.length/2的最大整數(shù) downto 1
3 MAX-HEAPIFY(A,i)
通過HEAPSORT進(jìn)行堆排序算法
所謂的堆排序算法,先通過前面的BUILD-MAX-HEAP將輸入數(shù)組A[1...n]建成最大堆,其中n=A.length。而數(shù)組中的元素總在根結(jié)點(diǎn)A[1]中,通過把它與A[n]進(jìn)行互換,就能將該元素放到正確的位置。
如何讓原來根的子結(jié)點(diǎn)仍然是最大堆呢,可以通過從堆中去掉結(jié)點(diǎn)n,而這可以通過減少A.heap?size來間接的完成。但這樣一來新的根節(jié)點(diǎn)就違背了最大堆的性質(zhì),因此仍然需要調(diào)用MAX-HEAPIFY(A,1),從而在A[1...n?1]上構(gòu)造一個(gè)新的最大堆。
通過不斷重復(fù)這一過程,知道堆的大小從n?1一直降到2即可。
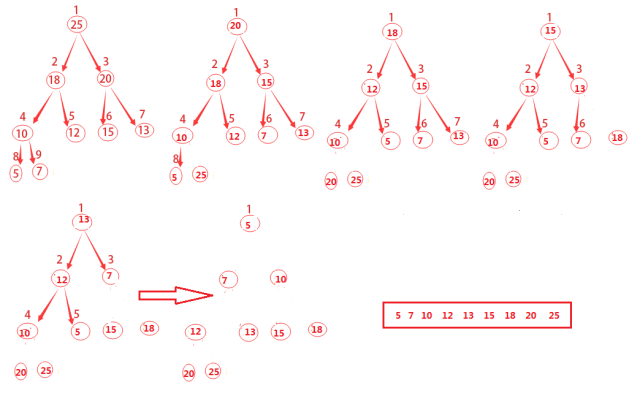
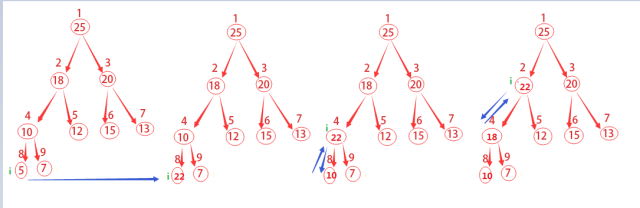
上圖的演進(jìn)方式主要有兩點(diǎn):
1)將A[1]和A[i]互換,i從A.length一直遞減到2
2)不斷調(diào)用MAX-HEAPIFY(A,1)對(duì)剩余的整個(gè)堆進(jìn)行重新構(gòu)建
一直到最后堆已經(jīng)不存在了。
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i=A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size=A.heap-size-1
5 MAX-HEAPIFY(A,1)
優(yōu)先隊(duì)列
下一篇博文我們就會(huì)介紹大名鼎鼎的快排,快速排序啦,歡迎童鞋們預(yù)定哦~
話說堆排序雖然性能上不及快速排序,但作為一個(gè)盡心盡力的數(shù)據(jù)結(jié)構(gòu)而言,其可謂業(yè)界良心吶。它還為我們提供了傳說中的“優(yōu)先隊(duì)列”。
優(yōu)先隊(duì)列(priority queue)和堆一樣,堆有最大堆和最小堆,優(yōu)先隊(duì)列也有最大優(yōu)先隊(duì)列和最小優(yōu)先隊(duì)列。
優(yōu)先隊(duì)列是一種用來維護(hù)由一組元素構(gòu)成的集合S的數(shù)據(jù)結(jié)構(gòu),其中每個(gè)元素都有一個(gè)相關(guān)的值,稱之為關(guān)鍵字(key)。
一個(gè)最大優(yōu)先隊(duì)列支持一下操作:
MAXIMUM(S):返回S中有著最大鍵值的元素。
EXTRACT?MAX(S):去掉并返回S中的具有最大鍵字的元素。
INCREASE?KEY(S,x,a):將元素x的關(guān)鍵字值增加到a,這里假設(shè)a的值不小于x的原關(guān)鍵字值。
INSERT(S,x):將元素x插入集合S中,這一操作等價(jià)于S=S∪{x}。
這里來舉一個(gè)最大優(yōu)先隊(duì)列的示例,我曾在關(guān)于“50% CPU 占有率”題目的內(nèi)容擴(kuò)展 這篇博文中簡(jiǎn)單介紹過Windows的系統(tǒng)進(jìn)程機(jī)制。
這里以圖片的形式簡(jiǎn)單的貼出來如下:
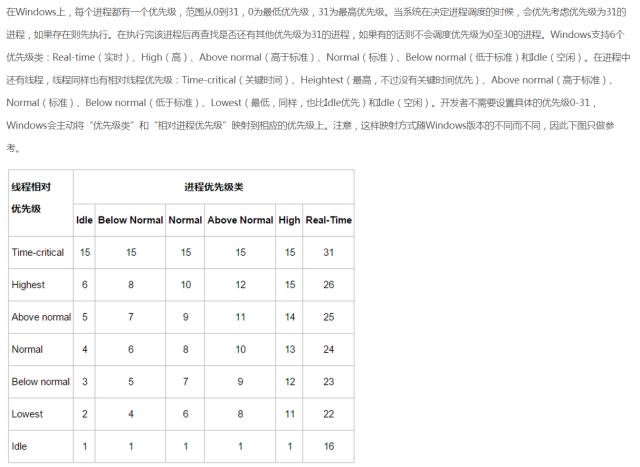
在用堆實(shí)現(xiàn)優(yōu)先隊(duì)列時(shí),需要在堆中的每個(gè)元素里存儲(chǔ)對(duì)應(yīng)對(duì)象的句柄(handle)。句柄的準(zhǔn)確含義依賴于具體的應(yīng)用程序,可以是指針,也可以是整型數(shù)。
在堆的操作過程中,元素會(huì)改變其在數(shù)組中的位置,因此在具體實(shí)現(xiàn)中,在重新確定堆元素位置時(shí),就自然而然地需要改變其在數(shù)組中的位置。
一、前面的MAXIMUM(S)過程其實(shí)很簡(jiǎn)單,完全可以在Θ(1)時(shí)間內(nèi)完成,因?yàn)橹恍枰祷財(cái)?shù)組的第一個(gè)元素就可以呀,它已經(jīng)是最大優(yōu)先隊(duì)列了嘛。
HEAP-MAXIMUM(A)
1 return A[1]
二、EXTRACT?MAX(S)就稍顯復(fù)雜了一點(diǎn),它的時(shí)間復(fù)雜度是O(lgn),因?yàn)檫@里面除了MAX-HEAPIFY(A,1)以外,其他的操作都是常量時(shí)間的。
HEAP-EXTRACT-MAX(A)
1 if A.heap-size < 1
2 error "堆下溢"
3 max=A[1]
4 A[1]=A[A.heap-size]
5 A.heap-size=A.heap-size-1
6 MAX-HEAPIFY(A,1)
7 return max
三、INCREASE?KEY(S,x,a)需要將一個(gè)大于元素x原有關(guān)鍵字值的a加到元素x上。
和上一個(gè)函數(shù)一樣,首先判斷a知否比原有的關(guān)鍵字更大。
然后就是老辦法了,不斷的將該結(jié)點(diǎn)與父結(jié)點(diǎn)做對(duì)比,如果父結(jié)點(diǎn)更小,那么就將他們進(jìn)行對(duì)換。
相信有圖示會(huì)更加清楚,于是……再來一張圖。
HEAP-INCREASE-KEY(A,i,key)
1 if key < A[i]
2 error "新關(guān)鍵字值比當(dāng)前關(guān)鍵字值更小"
3 A[i]=key
4 while i>1 and A[PARENT(i)] < A[i]
5 exchange A[i] with A[PARENT(I)]
6 i=PARENT(i)
在包含n個(gè)元素的堆上,HEAP-INCREASE-KEY的運(yùn)行時(shí)間就是O(lgn)了。因?yàn)樵诘?行做了關(guān)鍵字更新的結(jié)點(diǎn)到根結(jié)點(diǎn)的路徑長(zhǎng)度為O(lgn)。
四、INSERT(S,x)首先通過一個(gè)特殊的關(guān)鍵字(比如這里的-10000擴(kuò)展)結(jié)點(diǎn)來擴(kuò)展最大堆,然后調(diào)用HEAP-INCREASE-KEY來為新的結(jié)點(diǎn)設(shè)置對(duì)應(yīng)的關(guān)鍵字,同時(shí)保持最大堆的性質(zhì)。
MAX-HEAP-INSERT(A,key)
1 A.heap-size=A.heap-sieze+1
2 A[A.heap-size]=-10000
3 HEAP-INCREASE-KEY(A,A.hep-size,key)
在包含n個(gè)元素的堆上,MAX-HEAP-INSERT的運(yùn)行時(shí)間就是O(lgn)了。因?yàn)檫@個(gè)算法相對(duì)于上一個(gè)算法,除了HEAP-INCREASE-KEY之外就都是常量的運(yùn)行時(shí)間了,而HEAP-INCREASE-KEY的運(yùn)行時(shí)間我們?cè)谏弦徊糠忠呀?jīng)講過了。
總而言之,在一個(gè)包含n個(gè)元素的堆中,所有優(yōu)先隊(duì)列的操作時(shí)間都不會(huì)大于O(lgn)。
---END---
審核編輯 :李倩
-
算法
+關(guān)注
關(guān)注
23文章
4551瀏覽量
92017 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
568瀏覽量
40030 -
數(shù)組
+關(guān)注
關(guān)注
1文章
411瀏覽量
25821
原文標(biāo)題:五張圖帶你體會(huì)堆算法
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
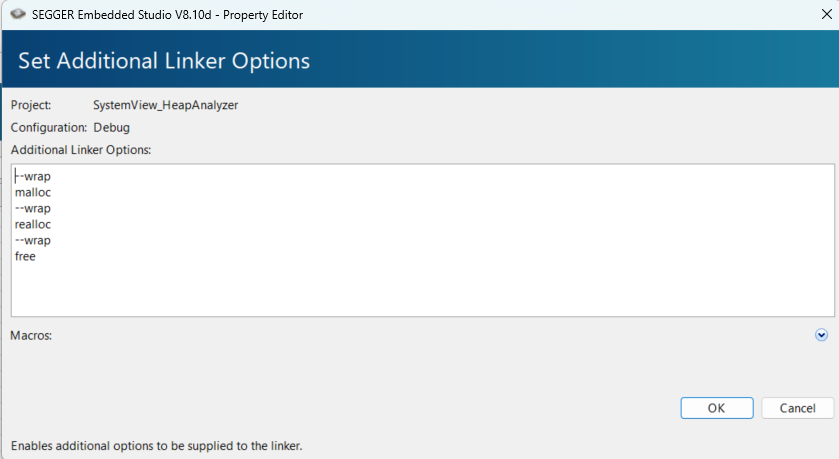
如何使用SystemView的堆監(jiān)控功能
單相整流橋堆怎么測(cè)量好壞
MDSC-1000C雙張傳感器在家電五金沖壓疊料檢測(cè)中的創(chuàng)新應(yīng)用

幫忙畫一張詳細(xì)的電路圖,謝謝
堆和棧的區(qū)別和使用注意事項(xiàng)
微軟用 AI 簡(jiǎn)化核反應(yīng)堆監(jiān)管審批流程;比亞迪獲首張 L3 級(jí)自動(dòng)駕駛測(cè)試牌照

20張圖帶你詳解EVPN
堆的實(shí)現(xiàn)思路
一張圖帶你回顧英特爾重磅亮相云棲大會(huì)的精彩瞬間

23張圖帶你弄懂HTTP協(xié)議!




 五張圖帶你體會(huì)堆算法
五張圖帶你體會(huì)堆算法












評(píng)論