原理

KNN屬于一種監督學習的分類算法，用于訓練的數據集是完全正確且已分好類的。

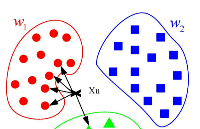
如果一個樣本在特征空間中的k個最相似(即特征空間中最鄰近)的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別。KNN算法的指導思想是“近朱者赤，近墨者黑”，由鄰居來推斷出類別。

「計算步驟如下：」

算距離：給定測試對象，計算它與訓練集中的每個對象的距離。包括閔可夫斯基距離、歐氏距離、絕對距離、切比雪夫距離、夾角余弦距離；

找鄰居：圈定距離最近的k個訓練對象，作為測試對象的近鄰；

做分類：根據這k個近鄰歸屬的主要類別，來對測試對象分類

「K的含義」：來了一個樣本x，要給它分類，即求出它的y，就從數據集中，在x附近找離它最近的K個數據點，這K個數據點，類別c占的個數最多，就把x的label設為c。K-近鄰法中的鄰近個數，即K的確定，是該方法的關鍵。

「優點：」

簡單，易于理解，易于實現，無需估計參數，無需訓練；

特別適合于多分類問題（對象具有多個類別標簽）。

「缺點：」

主要的不足：當樣本不平衡時，如一個類的 樣本容量很大，而其他類樣本容量很小時，有可能導致當輸入一個新樣本時，該樣本的K個鄰居中大容量類的樣本占多數。該算法只計算“最近的”鄰居樣本，某一類的樣本數量很大，那么或者這類樣本并不接近目標樣本，或者這類樣本很靠近目標樣本。

計算量較大，因為對每一個待分類的文本都要計算它到全體已知樣本的距離，才能求得它的K個最近鄰點。

可理解性差，無法給出像決策樹那樣的規則。

R 進行 KNN 的實例

#簡單示范，以iris數據集為例
train<-?iris[sample(nrow(iris),?145),]?#?訓練數據
test?<-?iris[sample(nrow(iris),?5),]?#?測試數據
head(test)
library(class)
aa?<-?knn(train?=?train[,1:4],?test?=?test[,1:4],?
??????????cl?=?train[,5],?k?=?5)
aa
table(test[,5],?aa)

輸出結果：

> head(test)
    Sepal.Length Sepal.Width Petal.Length Petal.Width   Species
117          6.5         3.0          5.5         1.8 virginica
135          6.1         2.6          5.6         1.4 virginica
44           5.0         3.5          1.6         0.6    setosa
18           5.1         3.5          1.4         0.3    setosa
43           4.4         3.2          1.3         0.2    setosa
> table(test[,5], aa)
            aa
             setosa versicolor virginica
  setosa          3          0         0
  versicolor      0          0         0
  virginica       0          0         2

「隨機數據進行KNN分類：」

#data
set.seed(12345)
x1<-?runif(60,-1,1)
x2?<-?runif(60,-1,1)??
y?<-?sample(c(0,1),size=60,replace=TRUE,prob=c(0.3,0.7))???
Data?<-?data.frame(Fx1=x1,Fx2=x2,Fy=y)??
SampleId?<-?sample(x=1:60,size=18)??
DataTest?<-?Data[SampleId,]???#?測試集
DataTrain?<-?Data[-SampleId,]??#?訓練集

par(mfrow=c(2,2),mar=c(4,6,4,4))
plot(Data[,1:2],pch=Data[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="全部樣本")
plot(DataTrain[,1:2],pch=DataTrain[,3]+1,cex=0.8,xlab="x1",ylab="x2",main="訓練樣本和測試樣本")
points(DataTest[,1:2],pch=DataTest[,3]+16,col=2,cex=0.8)

#?KNN?分類
library(class)
#?循環計算不同K時的錯誤率
##?測試集與訓練集均為Data時，會出現過擬合，錯誤率會很低
errRatio?<-?vector()??#?全部觀測的錯判率向量
for(i?in?1:30){
??KnnFit=knn(train=Data[,1:2],test=Data[,1:2],cl=Data[,3],k=i)
??CT=table(Data[,3],KnnFit)??#?計算混淆矩陣
??errRatio=c(errRatio,(1-sum(diag(CT))/sum(CT))*100)??#?計算錯判率（百分比）
}
plot(errRatio,type="l",xlab="鄰近個數K",ylab="錯判率(%)",main="ErrorRatio",ylim=c(0,80))
#?訓練集與測試集單獨分開
errRatio1?<-?vector()???#?測試樣本錯判率向量（旁置法）
for(i?in?1:30){
?KnnFit=knn(train=DataTrain[,1:2],test=DataTest[,1:2],cl=DataTrain[,3],k=i)?
?CT=table(DataTest[,3],KnnFit)?
?errRatio1=c(errRatio1,(1-sum(diag(CT))/sum(CT))*100)????
}
lines(1:30,errRatio1,lty=2,col=2)??#?隨著樣本數增加，錯誤率趨于穩定

#?使用另一個函數?knn.cv()，在不指定測試集的情況下默認使用訓練集
#?該函數使用留一法交叉驗證方法，與?knn?有區別，適用于樣本量少的情況
errRatio2<-vector()???#?留一法錯判率向量
for(i?in?1:30){???
?KnnFit<-knn.cv(train=Data[,1:2],cl=Data[,3],k=i)?
?CT<-table(Data[,3],KnnFit)??
?errRatio2<-c(errRatio2,(1-sum(diag(CT))/sum(CT))*100)?????
}
lines(1:30,errRatio2,col=2)

#?KNN?回歸
set.seed(12345)
x1?<-?runif(60,-1,1)?
x2?<-?runif(60,-1,1)?
y?<-?runif(60,10,20)???
Data?<-?data.frame(Fx1=x1,Fx2=x2,Fy=y)
SampleId?<-?sample(x=1:60,size=18)??
DataTest?<-?Data[SampleId,]??
DataTrain?<-?Data[-SampleId,]??
mseVector?<-?vector()????
for(i?in?1:30){
?KnnFit<-knn(train=DataTrain[,1:2],test=DataTest[,1:2],cl=DataTrain[,3],k=i,prob=FALSE)?
?#?回歸結果為因子向量，需轉換成數值型向量
?KnnFit<-as.double(as.vector(KnnFit))???
?mse<-sum((DataTest[,3]-KnnFit)^2)/length(DataTest[,3])???
?mseVector<-c(mseVector,mse)
}
plot(mseVector,type="l",xlab="近鄰個數?K",ylab="均方誤差",main="近鄰數K與均方誤差",ylim=c(0,80))

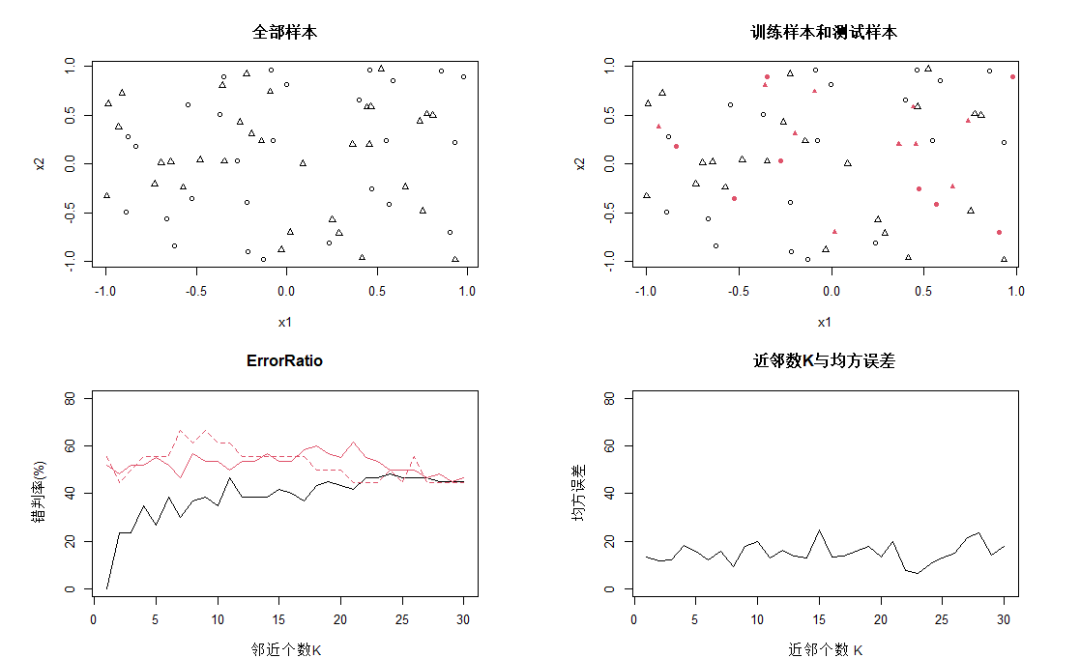
上圖中，第一幅圖為觀測全體在特征空間中的分布，三角和圈分別表示輸出變量的類別值分別為0和1；第二幅圖是訓練樣本集和測試樣本集的觀測分布，其中有填充色的點屬于測試樣本集；

第三幅圖黑線為全部觀測進入訓練樣本集時的錯判概率線，K=1時預測錯誤率一般為0；紅色虛線為旁置法的錯判概率曲線，K=9時達到最小；紅色實線為留一法錯判概率曲線，K=7時達到最小。「留一法的曲線基本在旁置法下方，應是較為客觀的預測錯誤估計」。第四幅圖是回歸預測時測試樣本集的均方誤差隨參數K變化的曲線。

KNN應用——天貓數據集

library(class)
Tmall_train<-read.table(file="天貓_Train_1.txt",header=TRUE,sep=",")
head(Tmall_train)
#???BuyOrNot?BuyDNactDN?ActDNTotalDN?BuyBBrand?BuyHit
#?1????????1???????6.38????????51.09??????2.83???1.57
#?2????????1???????8.93????????60.87??????3.20???2.17
#?3????????1??????16.13????????33.70?????11.63???6.36
#?4????????1??????16.22????????40.22?????11.29???6.25
#?5????????1???????3.85????????56.52??????1.89???1.45
#?6????????1???????4.00????????54.35??????2.13???1.28
Tmall_train$BuyOrNot<-as.factor(Tmall_train$BuyOrNot)
Tmall_test<-read.table(file="天貓_Test_1.txt",header=TRUE,sep=",")
head(Tmall_test)
#???BuyOrNot?BuyDNactDN?ActDNTotalDN?BuyBBrand?BuyHit
#?1????????0???????0.00????????54.84??????0.00???0.00
#?2????????1???????7.69????????83.87??????2.36???0.83
#?3????????1??????14.29????????90.32??????4.76???3.89
#?4????????1??????10.00????????32.26??????7.69???4.00
#?5????????1??????15.38????????41.94??????8.70???6.98
#?6????????0???????0.00????????19.35??????0.00???0.00
Tmall_test$BuyOrNot<-as.factor(Tmall_test$BuyOrNot)

模型方法同上：

#天貓成交顧客的分類預測
set.seed(123456)
errRatio<-vector()???
for(i?in?1:30){
?KnnFit<-knn(train=Tmall_train[,-1],test=Tmall_test[,-1],cl=Tmall_train[,1],k=i,prob=FALSE)?
?CT<-table(Tmall_test[,1],KnnFit)
?errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)
}
errorRation
#?[1]?1.707317?2.195122?2.804878?3.170732?3.292683?4.146341?3.292683?4.878049?5.975610?4.756098?5.365854?6.097561?6.341463?6.341463?6.341463?6.829268?8.048780
#?[18]?8.048780?8.048780?8.048780?8.048780?6.951220?6.829268?6.707317?8.048780?7.439024?8.048780?8.048780?8.048780?8.048780
plot(errRatio,type="b",xlab="近鄰個數?K",ylab="錯判率(%)",main="天貓成交顧客的分類預測")

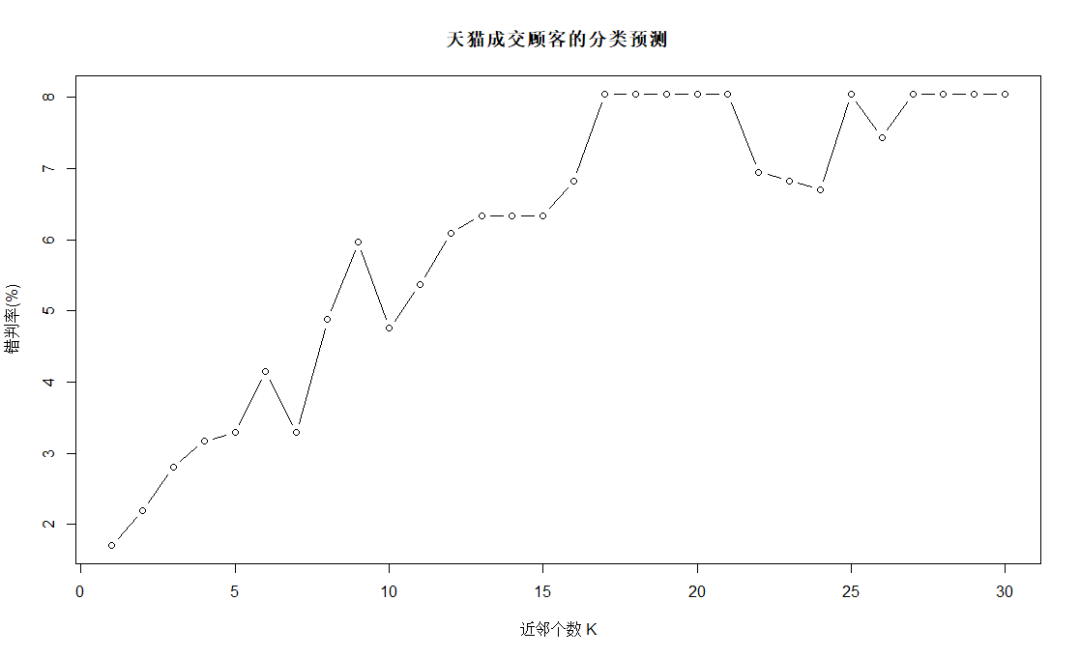
結合上圖并兼顧KNN分析的穩健性等考慮，采用K=7的分析結論，錯判率為3.3%。

基于變量重要性的加權KNN

KNN默認各輸入變量在距離測度中有“同等重要”的貢獻，但情況并不總是如此。因此需要采用基于變量重要性的加權KNN，計算加權距離，給重要變量賦予較高的權重，不需要的變量賦予較低的權重是必要的。

天貓數據KNN分類討論變量的重要性

library(class)
par(mfrow=c(2,2))
set.seed(123456)
errRatio<-vector()???
for(i?in?1:30){
?KnnFit<-knn(train=Tmall_train[,-1],test=Tmall_test[,-1],cl=Tmall_train[,1],k=i,prob=FALSE)?
?CT<-table(Tmall_test[,1],KnnFit)?
?errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)????
}
plot(errRatio,type="l",xlab="近鄰個數?K",ylab="錯判率(%)",main="鄰近數?K?與錯判率")
#?選擇一個錯判率相對較低的?K
errDelteX<-errRatio[7]
#?剔除變量
for(i?in?-2:-5){
?fit<-knn(train=Tmall_train[,c(-1,i)],test=Tmall_test[,c(-1,i)],cl=Tmall_train[,1],k=7)
?CT<-table(Tmall_test[,1],fit)
?errDelteX<-c(errDelteX,(1-sum(diag(CT))/sum(CT))*100)
}
plot(errDelteX,type="l",xlab="剔除變量",ylab="剔除錯判率(%)",main="剔除變量與錯判率(K=7)",cex.main=0.8)
xTitle=c("1:全體變量","2:消費活躍度","3:活躍度","4:成交有效度","5:活動有效度")
legend("topright",legend=xTitle,title="變量說明",lty=1,cex=0.6)
FI<-errDelteX[-1]+1/4
wi<-FI/sum(FI)
GLabs<-paste(c("消費活躍度","活躍度","成交有效度","活動有效度"),round(wi,2),sep=":")
pie(wi,labels=GLabs,clockwise=TRUE,main="輸入變量權重",cex.main=0.8)
ColPch=as.integer(as.vector(Tmall_test[,1]))+1
plot(Tmall_test[,c(2,4)],pch=ColPch,cex=0.7,xlim=c(0,50),ylim=c(0,50),col=ColPch,
?????xlab="消費活躍度",ylab="成交有效度",main="二維特征空間中的觀測",cex.main=0.8)

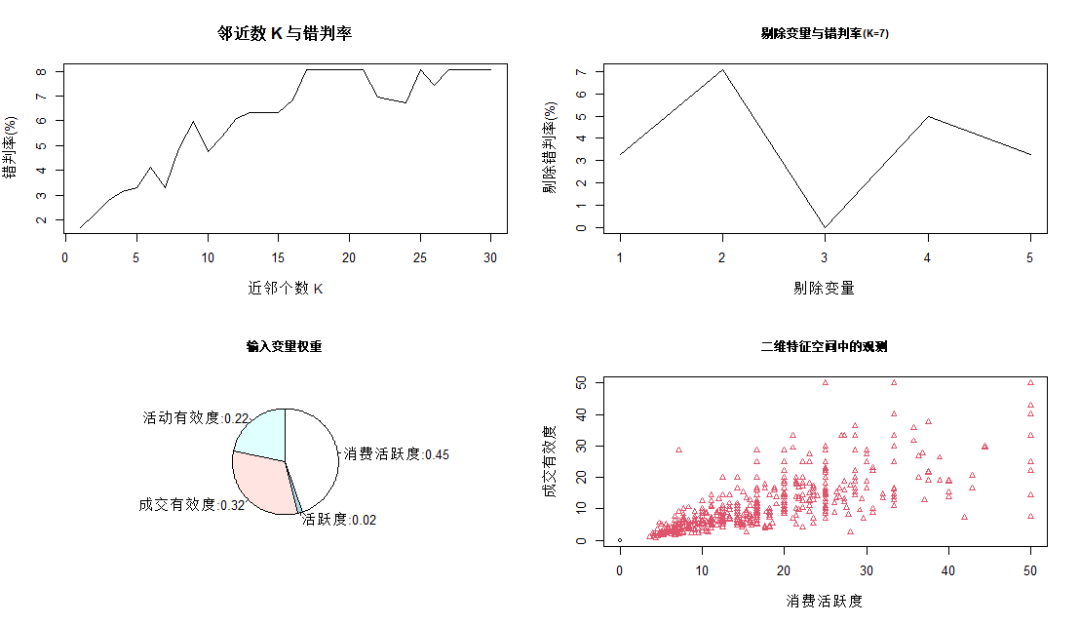
上圖中第一幅圖為普通KNN方法；

第二幅圖為確定K=7后，逐個剔除變量，剔除后的錯判率曲線（"1:全體變量","2:消費活躍度","3:活躍度","4:成交有效度","5:活動有效度"），可見剔除消費活躍度后錯判概率顯著增加，說明消費活躍度對預測的影響巨大；剔除活躍度后錯判概率大幅下降，說明該變量包含較強噪聲，對預測性能有負面影響；剔除成交有效性后錯判率也大幅上升，說明該變量對預測貢獻較大；

根據FI定義計算各個輸入變量的重要性，確定的權重如第三幅圖；第四幅圖是消費活躍度和成交有效度特征空間中觀測點的分布情況，黑色圓圈表示無成交，紅色三角表示有成交，可見所有無交易點均在消費活躍度和成交有效度等于0處，消費活躍度和成交有效度大于0則均為有成交。

?

綜上，結論如下：

①在近鄰數K=7時，普通KNN方法對測試樣本集的錯判率僅為3.3%，效果較好；

②大部分成交顧客處于消費活躍度和成交有效性取值水平較低的位置，在消費活躍度和成交有效性上取值較高處的成交顧客數量很少，可作為日后顧客營銷策略的參考依據

?

基于觀測相似性的加權KNN

#devtools::install_github("KlausVigo/kknn")
library("kknn")
#kknn(formula=R公式,train=訓練樣本集,test=測試樣本集,na.action=na.omit(),k=鄰近個數K,distance=k,kernel=核名稱)
par(mfrow=c(2,1))
Tmall_train<-read.table(file="天貓_Train_1.txt",header=TRUE,sep=",")
Tmall_train$BuyOrNot<-as.factor(Tmall_train$BuyOrNot)
fit<-train.kknn(formula=BuyOrNot~.,data=Tmall_train,kmax=11,distance=2,kernel=c("rectangular","triangular","gaussian"),na.action=na.omit())
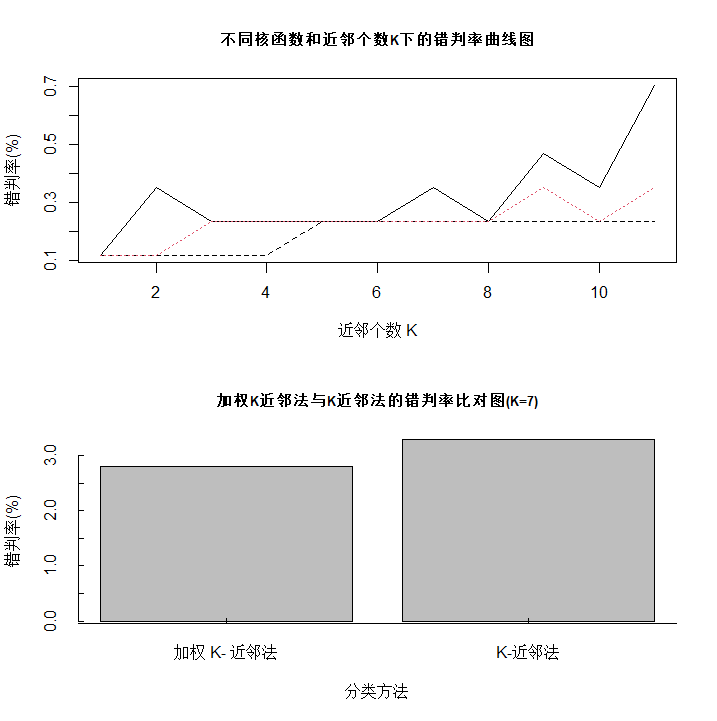
plot(fit$MISCLASS[,1]*100,type="l",
?????main="不同核函數和近鄰個數K下的錯判率曲線圖",cex.main=0.8,xlab="近鄰個數?K",ylab="錯判率(%)")
lines(fit$MISCLASS[,2]*100,lty=2,col=1)
lines(fit$MISCLASS[,3]*100,lty=3,col=2)
legend("topleft",legend=c("rectangular","triangular","gaussian"),lty=c(1,2,3),col=c(1,1,2),cex=0.7)
#?利用加權?K?近鄰分類
Tmall_test<-read.table(file="天貓_Test_1.txt",header=TRUE,sep=",")
Tmall_test$BuyOrNot<-as.factor(Tmall_test$BuyOrNot)
fit<-kknn(formula=BuyOrNot~.,train=Tmall_train,test=Tmall_test,k=7,distance=2,kernel="gaussian",na.action=na.omit())
CT<-table(Tmall_test[,1],fit$fitted.values)
errRatio<-(1-sum(diag(CT))/sum(CT))*100
#?利用?K?近鄰分類
library("class")
fit<-knn(train=Tmall_train,test=Tmall_test,cl=Tmall_train$BuyOrNot,k=7)
CT<-table(Tmall_test[,1],fit)
errRatio<-c(errRatio,(1-sum(diag(CT))/sum(CT))*100)
errGraph<-barplot(errRatio,main="加權K近鄰法與K近鄰法的錯判率比對圖(K=7)",
??????????????????cex.main=0.8,xlab="分類方法",ylab="錯判率(%)",axes=FALSE)
axis(side=1,at=c(0,errGraph,3),labels=c("","加權?K-?近鄰法","K-近鄰法",""),tcl=0.25)
axis(side=2,tcl=0.25)

決策樹&隨機森林

原理

決策樹的目標是建立分類預測模型或回歸預測模型。決策樹(decision tree)也稱判定樹，它是由對象的若干屬性、屬性值和有關決策組成的一棵樹。其中的節點為屬性（一般為語言變量），分枝為相應的屬性值（一般為語言值）。從同一節點出發的各個分枝之間是邏輯“或”關系；根節點為對象的某一個屬性；從根節點到每一個葉子節點的所有節點和邊，按順序串連成一條分枝路徑，位于同一條分枝路徑上的各個“屬性-值”對之間是邏輯“與”關系，葉子節點為這個與關系的對應結果，即決策屬性。

「根節點」：決策樹最上層的點，一棵決策樹只有一個根節點；

「葉節點」：沒有下層的節點稱為葉節點；

「中間節點」：位于根節點下且自身有下層的節點。中間節點可分布在多個層中，同層節點稱為兄弟節點。上層節點是下層節點的父節點，下層節點是上層節點的子節點。根節點沒有父節點，葉節點沒有子節點。

**2 叉樹和多叉樹 **：若樹中每個節點最多只能長出兩個分枝，即父節點只能有兩個子節點，這樣的決策樹稱為2叉樹。若能長出不止兩個分枝，即父節點有兩個以上的子節點，這樣的決策樹稱為多叉樹。

?

決策樹分為分類樹和回歸樹，分別對應分類預測模型和回歸預測模型，分別用于對分類型和數值型輸出變量值的預測。

?

決策樹主要圍繞兩個核心問題展開：

「決策樹的生長」。即利用訓練樣本集完成決策樹的建立過程。決策樹一般不建立在全部觀測樣本上，通常需首先利用旁置法，將全部觀測樣本隨機劃分訓練樣本集和測試樣本集。在訓練樣本集上建立決策樹，利用測試樣本集估計決策樹模型的預測誤差；

「決策樹的剪枝」。即利用測試樣本集對所形成的決策樹進行精簡。

分類回歸樹的R實現

rpart(輸出變量~輸入變量,data=數據框名,method=方法名,parms=list(split=異質性測度指標),control=參數對象名)
#數據事先組織在 data 參數指定的數據框中；
#輸出變量~輸入變量是R公式的寫法，若建立分類樹，輸出變量應為因子，若有多個輸入變量，需用加號連接；
#參數 method 用于指定方法，可取值：“class”表示建立分類樹，“position”和“anova”分別輸出變量為計數變量和其他數值型變量，此時建立回歸樹；
#參數 parms 用于指定分類樹的異質性測度指標，可取值：“gini”表示采用Gini系數，“information”表示采用信息熵；
#參數control用于設定預修剪參數、后修剪中的復雜度參數CP值

設置預修剪等參數的 R 函數：

rpart.control(minsplit=20,maxcompete=4,xval=10,maxdepth=30,cp=0.01)
# minsplit：指定節點最小樣本量，默認為20
# maxcompete：指定按變量重要性降序，輸出當前最佳分組變量的前若干個候選變量，默認為4
# xval：指定進行交叉驗證剪枝時的交叉折數，默認為10
# maxdepth：指定最大樹深度，默認為30
# cp：指定最小代價復雜度剪枝中的復雜度CP參數值，默認為0.01

?

當參數 cp 采用默認值 0.01 且 R 給出的決策樹過小時（由于0.01過大的結果），可適當減小 cp 參數值。如可指定參數 cp 為 0，此時的決策樹是滿足預修剪參數下的未經后修剪的最大樹，實際應用中這棵樹可能過于茂盛。再次基礎上，R 將依次給出 CP 值從 0 開始并逐漸增大過程中經過若干次修剪后的決策樹。

?

可視化決策樹的 R 函數：

rpart.plot(決策樹結果對象名,type=編號,branch=外形編號,extra=1)
#決策樹對象名：rpart 函數返回對象；
# type：決策樹展示方式。可取值：0~4；
# branch：指定決策樹外形，可取0（斜線連接）和 1（垂線連接）；
# extra：指定在節點中顯示哪些數據。可取1~9

復雜參數 CP 對預測誤差的影響：

#復雜度參數 CP 是決策樹剪枝的關鍵參數，其設置是否合理直接決定決策樹是否過于復雜而出現過擬合，或是否過于簡單而無法得到理想的預測精度。可通過函數 printcp 和 plotcp 瀏覽與可視化 cp 值：
printcp(決策樹結果對象名)
plotcp(決策樹結果對象名)

分類回歸樹的應用：提煉不同消費行為顧客的主要特征

1.初建分類樹

#install.packages("rpart")
#install.packages("rpart.plot")
library(rpart)
library(rpart.plot)
BuyOrNot<-read.table(file="消費決策數據.txt",header=TRUE)
BuyOrNot$Income<-as.factor(BuyOrNot$Income)?#指定收入為因子
BuyOrNot$Gender<-as.factor(BuyOrNot$Gender)?#?指定性別為因子
#?指定預修剪等參數，復雜度參數CP為?0
Ctl?<-?rpart.control(minsplit=2,maxcompete=4,xval=10,maxdepth=10,cp=0)
set.seed(12345)
TreeFit1?<-?rpart(Purchase~.,data=BuyOrNot,method="class",
????????????????parms=list(split="gini"),control=Ctl)
rpart.plot(TreeFit1,type=4,branch=0,extra=2)
printcp(TreeFit1)?#?可視化CP值
plotcp(TreeFit1)

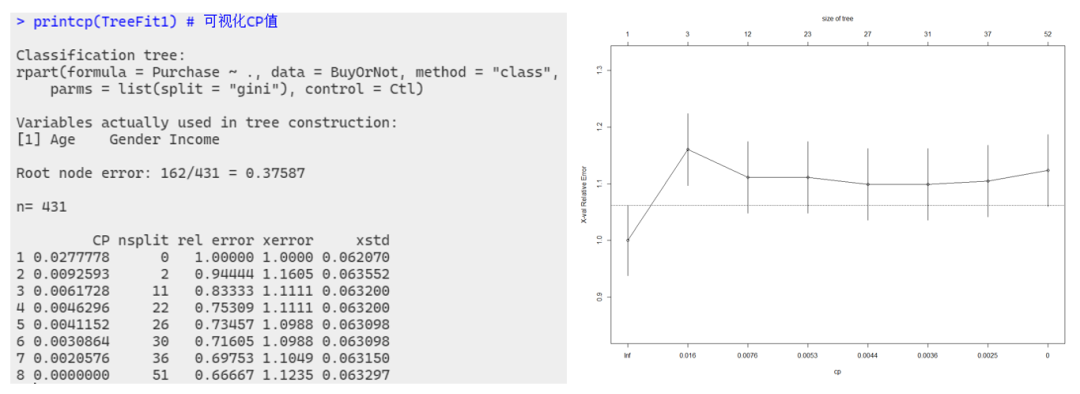
結果顯示，根節點包括全部 431 個觀測樣本，其中「162 個輸出變量值為1的觀測被誤判為0，錯判率為 38%」。左圖中，（不含序號）第1列為CP值，第2列 nsplit 為樣本數據共經過的分組次數，第3列 rel error 是預測誤差相對值的估計，第4列 xerror 是交叉驗證的預測誤差相對值，第 5 列 xstd 為預測誤差的標準誤。

需要注意的是，這里的第 3~4 列給出的是以根節點預測誤差為單位1的相對值。例如：本例中根節點的預測錯誤率162/431為單位1，經2次分組得到3個葉節點的分類樹，因錯誤相對值為0.944，所以該樹總的預測錯誤率為153/431。

當復雜度參數 CP 取指定值 0 時，此時的分類樹是經過51次分組的結果，包含52個葉節點，與右圖對應。此時分類樹的預測誤差估計值為0.667。經過交叉驗證，在CP參數增加至0.002過程中進行了若干次剪枝，此時決策樹是36次分組后的結果，包含37個節點，預測誤差相對值為0.698，增加了0.031個單位。

右圖縱坐標為根節點的交叉驗證預測誤差為單位 1 時，當前決策樹的交叉驗證預測誤差的單位數；橫坐標從右往左是 CP 列表中 8 個 CP 值的典型代表值 β，上方對應的是當前決策樹所包含的葉節點個數。可以看出，「包含 12 個葉節點的決策樹有最低的交叉驗證預測誤差」。

2.再建分類樹

set.seed(12345)
#默認參數
(TreeFit2<-rpart(Purchase~.,data=BuyOrNot,method="class",parms=list(split="gini")))
TreeFit2
rpart.plot(TreeFit2,type=4,branch=0,extra=2)??#?可視化決策樹
printcp(TreeFit2)??#?顯示復雜度CP參數列表

#?指定?cp=0.008，建立前述包含12個葉節點的決策樹
TreeFit3<-prune(TreeFit1,cp=0.008)?
rpart.plot(TreeFit3,type=4,branch=0,extra=2)
printcp(TreeFit3)
plotcp(TreeFit3)

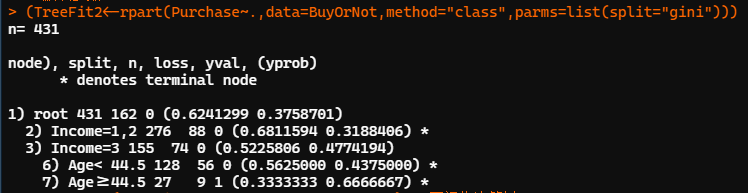
上圖是按系統默認參數構建決策樹，CP 參數為默認初始值 0.01，異質性指標采用 Gini 系數。節點2后的星號*標記表示為葉節點，其中所有觀測的 Income 取 1 或 2，樣本量為 276，其中 88 個輸出變量為 1 的觀測點被誤判為 0，置信度為0.68，錯判率 0.32。其余同理。

?

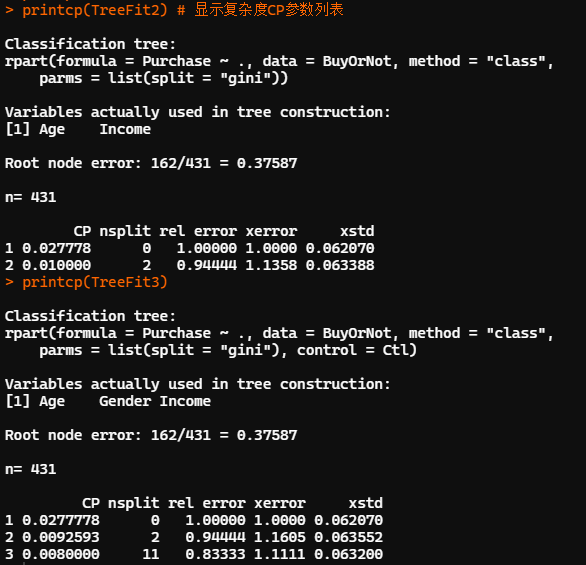
「分類回歸樹只能建立 2 叉樹」

?

建立分類回歸樹的組合預測模型：給出穩健預測

分類回歸樹具有不穩定性，模型會隨訓練樣本的變化而劇烈變動。組合預測模型是提高模型預測精度和穩健性的有效途徑，其首要工作是基于樣本數據建立一組模型而非單一模型；其次，預測時由這組模型同時提供各自的預測結果，通過類似“投票表決”的形式決定最終的預測結果。

組合預測中的單個模型稱為「基礎學習器（Base Learner）」，通常有相同的模型形式，如決策樹或其他預測模型等。多個預測模型是建立在多個樣本集合上的。

如何獲得多個樣本集合，以及如何將多個模型組合起來實現更合理的“投票表決”，是組合模型預測中的兩個重要方面。對此，常見的技術有「袋裝（Bagging）技術」和「推進（Boosting）技術」。

1.袋裝技術的 R 實現

#ipred包中的bagging函數
bagging(輸出變量名~輸出變量名,data=數據框名,nbagg=k,coob=TRUE,control=參數對象名)
#輸出變量名~輸入變量名為 R 公式的寫法，有多個輸入變量時應用加號連接；
#coob=TRUE表示基于袋裝觀測（OOB）計算預測誤差
# control：指定袋裝過程所建模型的參數。bagging函數的內嵌模型，即基礎學習器為分類回歸樹，control參數應為rpart函數的參數
# nbagg：指定自舉次數為 k，默認重復 25 次自舉過程，生成 25顆分類回歸樹

#adabag包中的bagging函數
bagging(輸出變量名~輸出變量名,data=數據框名,mfinal=重復次數,control=參數對象名)
# mfinal：指定重復幾次自舉過程，默認為100。bagging函數的基礎學習器為分類樹，control參數應為rpart函數的參數
# bagging函數返回值是列表。tree成分中存儲k顆分類樹的結果；votes中存儲k個模型的投票情況；prob中存儲預測類別的概率值；class為預測類別；importance為輸入變量對輸出變量預測重要性的得分
#對新樣本集進行預測：predict.bagging 函數
predict.bagging(bagging結果對象名,新樣本集名)
# predict.bagging 將返回名為 votes，prob，class的列表成分，含義同bagging函數。此外，還返回名為confusion和error的列表成分，分別存儲混淆矩陣和錯判率

2.袋裝技術的應用：穩健定位目標客戶

library(rpart)
MailShot<-read.table(file='郵件營銷數據.txt',header?=?T)
MailShot<-MailShot[,-1]??#?剔除ID
Ctl?<-?rpart.control(minsplit=20,maxcompete=4,maxdepth=30,
?????????????????????cp=0.01,xval=10)?#?rpart的默認參數
set.seed(12345)
TreeFit?<-?rpart(MAILSHOT~.,data=MailShot,
?????????????????method="class",?parms=list(split="gini"))??#?建立單一分類樹
rpart.plot(TreeFit,type=4,branch=0,extra=1)
CFit1<-predict(TreeFit,MailShot,type="class")??#?利用單個分類樹對全部觀測進行預測
#?CFit1<-predict(TreeFit,MailShot)??
ConfM1<-table(MailShot$MAILSHOT,CFit1)??#?計算單個分類樹的混淆矩陣
#??????CFit1
#????????NO?YES
#???NO??119??46
#???YES??39??96
(E1?<-(sum(ConfM1)-sum(diag(ConfM1)))/sum(ConfM1))?#?計算單個分類樹的錯判率
#?0.2833333

首先建立單個分類樹，并利用單個分類樹對全部觀測做預測，錯判率為 0.28。

##利用ipred包中的bagging建立組合分類樹
library(ipred)
set.seed(12345)
MailShot$MAILSHOT<-?as.factor(MailShot$MAILSHOT)??#?不轉換數據類型一直報錯
(BagM1<-bagging(MAILSHOT~.,data=MailShot,nbagg=25,
????????????????coob=TRUE,control=Ctl))??#?bagging建立分類組合樹
CFit2<-predict(BagM1,MailShot,type="class")??#?利用組合分類樹對全部觀測進行預測
ConfM2<-table(MailShot$MAILSHOT,CFit2)??#?計算組合分類樹的混淆矩陣
(E2<-(sum(ConfM2)-sum(diag(ConfM2)))/sum(ConfM2))??#?計算組合分類樹的錯判率
#?0.196667

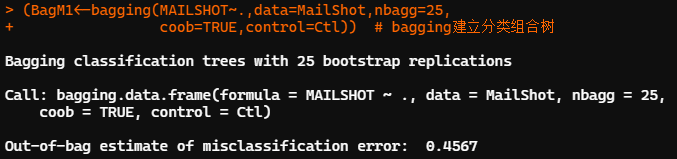
利用 ipred 包中的 bagging 函數建立組合分類樹，袋裝過程默認進行28次重抽樣自舉，生成25顆分類樹。基于袋外觀測（OOB）的預測誤差為0.457。利用組合分類樹并對全部觀測做預測，錯判率為 0.197。「預測精度較單一分類樹有一定提高」

predict 函數 type 指定為 class 時，給出的預測結果時分類值。不指定參數，默認給出的預測結果是各類別的概率值（預測置信度）。

##利用adabag包中的bagging函數
detach("package:ipred")
library(adabag)
MailShot<-read.table(file="郵件營銷數據.txt",header=TRUE)
MailShot<-MailShot[,-1]
Ctl<-rpart.control(minsplit=20,maxcompete=4,maxdepth=30,cp=0.01,xval=10)
set.seed(12345)
BagM2<-bagging(MAILSHOT~.,data=MailShot,control=Ctl,mfinal?=?25)
BagM2$importance
#???????AGE???????CAR????GENDER????INCOME???MARRIED??MORTGAGE????REGION??????SAVE?
#?17.761337??3.202805??6.126779?49.217348??7.539829??5.398284??8.425630??2.327989?

CFit3<-predict.bagging(BagM2,MailShot)??#?利用組合分類樹對全部觀測進行預測
CFit3$confusion
CFit3$error

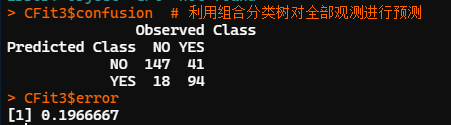
adabag 包中的 bagging 函數建立組合分類樹，參數設置同前。函數自動計算了輸入變量重要性的測度結果，并進行了歸一化處理。輸出變量重要性為歸一化后的百分比。本例中較為重要的兩個輸入變量依次為收入（INCOME）和年齡（AGE）。

用組合分類樹對全部觀測做預測的錯判率為，預測精度較單一分類樹有一定提高。

3.推進技術的 R 實現

袋裝技術中，自舉樣本的生成完全是隨機的。多個模型在預測投票中的地位也都相同，未考慮不同模型預測精度的差異性。推進技術在這兩方面進行了調整，其中的AdaBoost（Adaptive Boosting）策略已有較為廣泛的應用。

與袋裝技術不同的是，AdaBoost 采用的是加權投票方式，不同的模型具有不同的權重，權重大小與模型的預測誤差成反比。預測誤差較小的模型有較高的投票權重，預測誤差較大的模型投票權重較低。可見，「權重越高的模型，對決策結果的影響越大」。

#adabag包中的boosting函數
boosting(輸出變量名~輸入變量名,data=數據框,mfinal=重復次數,
boos=TRUE,coeflearn=模型權重調整方法,control=參數對象名)
#指定重復自舉次數，默認100
#boos=TRUE表示每次自舉過程均調整各觀測進入訓練樣本集的權重
# coeflearn：指定預測時各模型的權重設置方法。可取值 Breiman 或 Freund 或 zhu
#boosting函數的基礎學習器為分類樹，control參數應為rpart的默認參數

bagging函數返回值是列表。tree成分中存儲k顆分類樹的結果；votes中存儲k個模型的投票情況；prob中存儲預測類別的概率值；class為預測類別；importance為輸入變量對輸出變量預測重要性的得分；weight為各個模型的預測權重。

4.推進技術的應用：文件定位目標客戶

library(adabag)
MailShot<-?read.table(file="郵件營銷數據.txt",header?=?T)
MailShot<-MailShot[,-1]
MailShot$MAILSHOT?<-?as.factor(MailShot$MAILSHOT)
Ctl<-rpart.control(minsplit=20,maxcompete=4,maxdepth=30,cp=0.01,xval=10)
set.seed(12345)
BoostM<-boosting(MAILSHOT~.,data=MailShot,boos=TRUE,mfinal=25,
?????????????????coeflearn="Breiman",control=Ctl)
BoostM$importance
#???????AGE???????CAR????GENDER????INCOME???MARRIED??MORTGAGE????REGION??????SAVE?
#?23.666103??3.821141??3.597499?43.118805??5.424618??4.782976?11.057369??4.531490
ConfM4<-table(MailShot$MAILSHOT,BoostM$class)
E4?<-?(sum(ConfM4)-sum(diag(ConfM4)))/sum(ConfM4)
E4
#?0.02666667

本例中，較為重要的兩個輸入變量依次為收入和年齡。用組合分類樹對全部觀測做預測的錯判率為 0.027，較單一分類樹有顯著提高。

?

袋裝技術與推進技術有類似的研究目標，但兩者訓練樣本集的生成方式不同，組合預測方式也不同。兩者均可有效地提高預測準確性。「在大多數數據集中，推進技術的準確性一般高于袋裝技術，但也可能導致過擬合問題。」

?

隨機森林：具有隨機性的組合預測

Random Forest 也是一種組合預測模型，是用隨機方式建立一片森林，森林中包含眾多有較高預測精度且弱相關甚至不相關的決策樹，并形成組合預測模型；后續，眾多預測模型將共同參與對新觀測輸出變量取值的預測。

隨機森林的內嵌模型，即基礎學習器是分類回歸樹，其特色在于隨機，表現在兩個方面：

訓練樣本是對原始樣本的重抽樣自舉，訓練樣本具有隨機性；

在每顆決策樹的建立過程中，稱為當前最佳分組變量的輸入變量，是輸出變量全體的一個隨機候選變量子集中的競爭獲勝者。分組變量具有隨機性

「Bagging方法的主要過程：」

訓練分類器。從整體樣本集合中，抽樣n* < N個樣本 針對抽樣的集合訓練分類器Ci

分類器進行投票，最終的結果是分類器投票的優勝結果

隨機森林是以決策樹為基本分類器的一個集成學習模型，它包含多個由Bagging集成學習技術訓練得到的決策樹。前面描述了原始的樹的bagging算法。Random Forests不同的是：在Bagging的基礎上，他們使用一種改進的樹學習算法，這種樹學習算法在每個候選分裂的學習過程中，選擇特征值的一個隨機子集。這個過程有時被稱為“「feature bagging」”。

以決策樹為基本模型的bagging在每次bootstrap放回抽樣之后，產生一棵決策樹，抽多少樣本就生成多少棵樹，在生成這些樹的時候沒有進行更多的干預。而隨機森林也是進行bootstrap抽樣，但它與bagging的區別是在生成每棵樹的時候，每個節點變量都僅僅在隨機選出的少數變量中產生。因此，不但樣本是隨機的，連每個節點變量（Features）的產生都是隨機的。

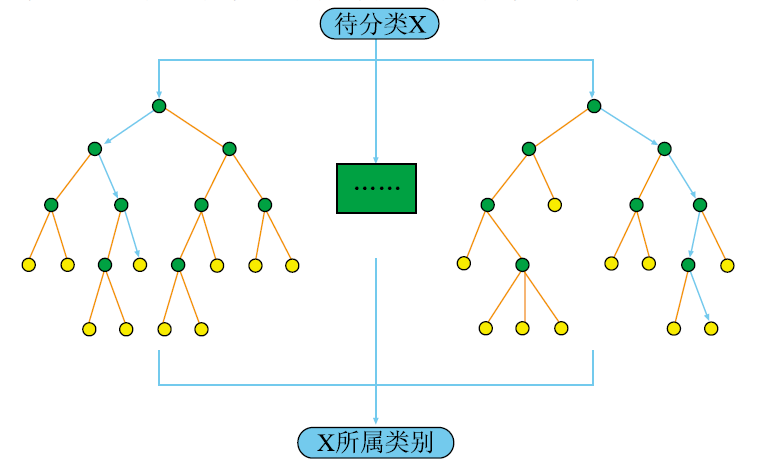
「隨機森林分類性能的主要因素：」

森林中單顆樹的分類強度（Strength）：每顆樹的分類強度越大，則隨機森林的分類性能越好。

森林中樹之間的相關度（Correlation）：樹之間的相關度越大，則隨機森林的分類性能越差。

「隨機森林的幾個理論要點：」

收斂定理。它度量了隨機森林對給定樣本集的分類錯誤率。

泛化誤差界。單個決策樹的分類強度越大，相關性越小，則泛化誤差界越小，隨機森林分類準確度越高。

袋外估計。Breiman在論文中指出袋外估計是無偏估計，袋外估計與用同訓練集一樣大小的測試集進行估計的精度是一樣的。

「隨機森林的優點：」

對于很多種資料，它可以產生高準確度的分類器。

它可以處理大量的輸入變量。

它可以在決定類別時，評估變量的重要性。

在建造隨機森林時，它可以在內部對于一般化后的誤差產生無偏差的估計。

它包含一個好方法可以估計遺失的資料，并且，如果有很大一部分的資料遺失，仍可以維持準確度。

它提供一個實驗方法，可以去偵測 variable interactions 。

對于不平衡的分類資料集來說，它可以平衡誤差。

它計算各例中的親近度，對于數據挖掘、偵測偏離者（outlier）和將資料視覺化非常有用。

使用上述。它可被延伸應用在未標記的資料上，這類資料通常是使用非監督式聚類。也可偵測偏離者和觀看資料。

學習過程是很快速的。

可以實現并行運行

「隨機森林的缺點：」

隨機森林已經被證明在某些噪音較大的分類或回歸問題上會過擬

對于有不同級別的屬性的數據，級別劃分較多的屬性會對隨機森林產生更大的影響，所以隨機森林在這種數據上產出的屬性權值是不可信的。

由于隨機選擇屬性，得單棵決策樹的的預測效果很差

投票機制中，并不是所有的樹都能夠準確地標記出所有的對象。

「隨機森林的應用：」

隨機森林是現在研究較多一種數據挖掘算法，由于其良好的性能表現，在現實生活中也獲得了廣泛的應用。隨機森林主要應用于回歸和分類。

隨機森林的 R 實現

#randomForest包中的randomForst函數
randomForest(輸出變量名~輸入變量名,data=數據框名,mtyr=k,ntree=M,importance=TRUE)
# mtry：指定決策樹各節點的輸入變量個數 k。若輸出變量為因子，隨機森林中的基礎學習器為分類樹；若為數值型變量，則基礎學習器為回歸樹；
# ntree：指定隨機森林包含 M 顆決策樹，默認為 500；
# importance = TRUE：表示計算輸入變量對輸出變量重要性的測度值

randomForets 函數的返回值為列表，包含以下成分：

predicted：基于袋外觀測 OOB 的預測類別或預測值；
confusion：基于袋外觀測 OOB 的混淆矩陣；
votes：適用于分類樹。給出各預測類別的概率值，即隨機森林中有多少臂力的分類樹投票給第 i 個類別；
oob.times：各個觀測值作為 OOB 的次數，即在重抽樣自舉中有多少次未進入自舉樣本，其會影響基于袋外觀測 OOB 的預測誤差結果；
err.rate：隨機森林中各個決策樹基于 OOB 的整體預測錯誤率，以及對各個類別的預測錯誤率；
importance：輸入變量重要性測度矩陣。

隨機森林的應用：文件定位客戶目標

library(randomForest)
MailShot<-read.table(file="郵件營銷數據.txt",?header?=?T)
MailShot<-MailShot[,-1]
set.seed(12345)
(rFM<-randomForest(MAILSHOT~.,data=MailShot,importance=TRUE,proximity=TRUE))
head(rFM$votes)??#?各觀測的各類別預測概率
head(rFM$oob.times)??#?各觀測作為?OOB?的次數

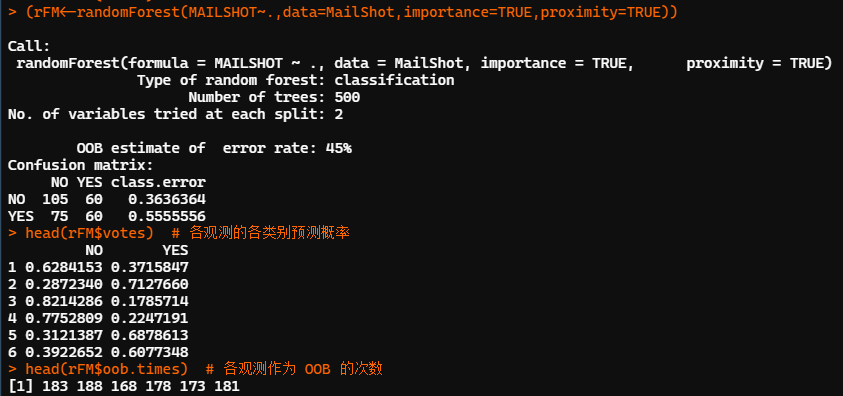
隨機森林共建了500顆決策樹，每個節點的候選輸入變量個數為2。基于袋外觀測 OOB 的預測錯判率為 45%。從袋外觀測的混淆矩陣看，模型對兩個類別的預測精度均不理想。對NO類的預測錯誤率為36.4%，對YES類的預測錯誤率為55.6%。

以第一個觀測為例：有62.8%的決策樹投票給NO，37.2%的決策樹投票給YES。有183次作為OOB未進入訓練樣本集。

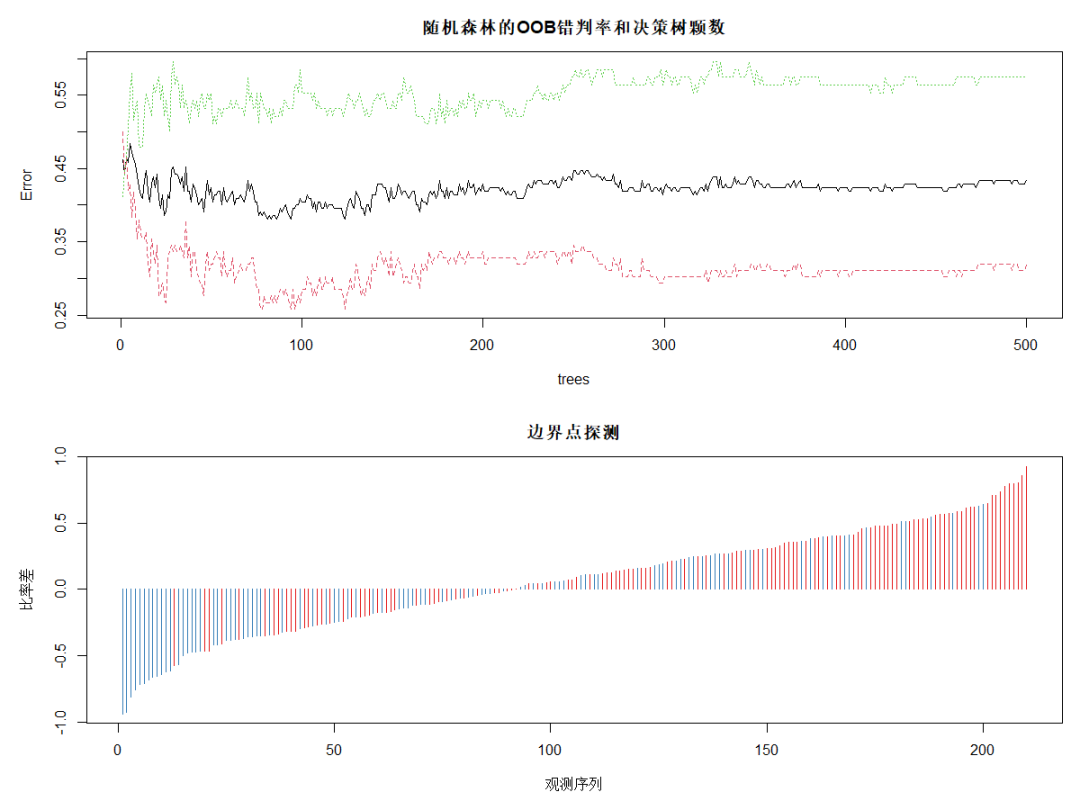
DrawL<-par(mfrow=c(2,1),mar=c(5,5,3,1))
plot(rFM,main="隨機森林的OOB錯判率和決策樹顆數")
plot(margin(rFM),type="h",main="邊界點探測",
?????xlab="觀測序列",ylab="比率差")?#?探測邊界點
par(DrawL)
Fit<-predict(rFM,MailShot)??#?隨機森林對全部觀測做預測
ConfM5<-table(MailShot$MAILSHOT,Fit)??#?隨機森林對全部觀測做預測的混淆矩陣
(E5<-(sum(ConfM5)-sum(diag(ConfM5)))/sum(ConfM5))??#?隨機森林的整體錯判率
#?0.03

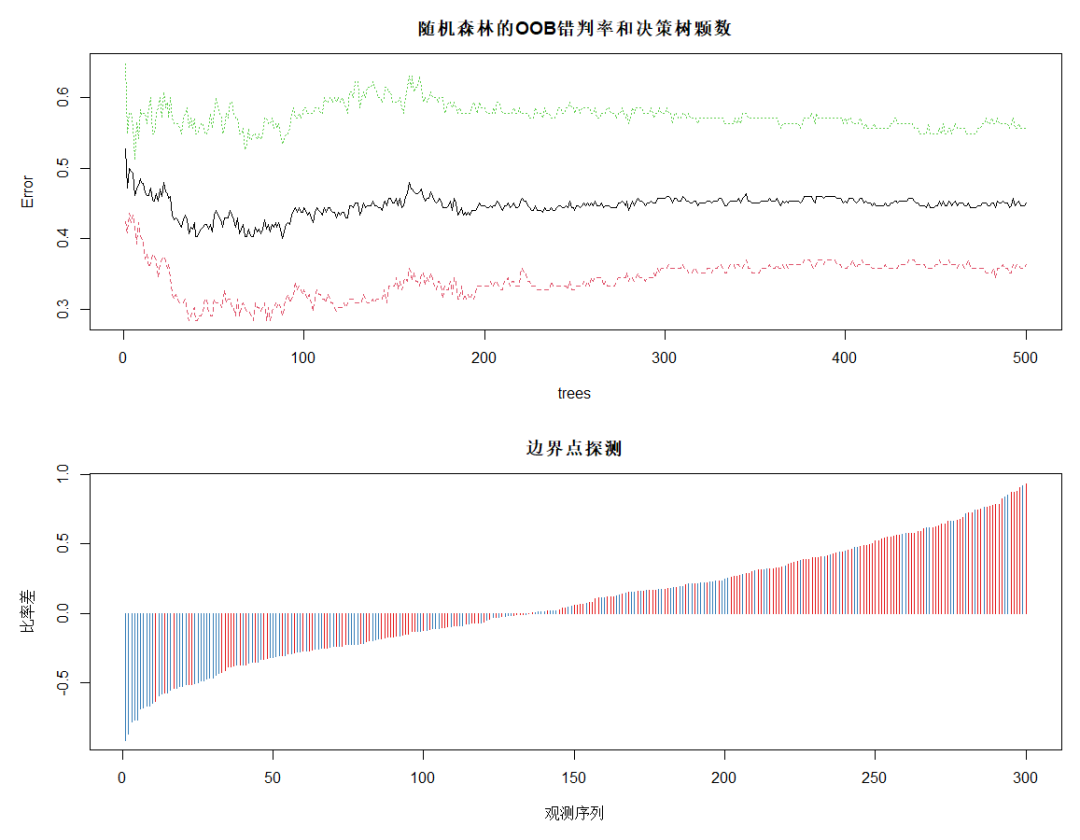
對OOB錯判率隨隨機森林中決策樹數量的變化特點進行可視化，plot的繪圖數據為err.rate。圖中黑色線為整體錯判率，紅色線為對NO類預測的錯判率，綠色線為對YES類預測的錯判率。可見，模型對NO類的預測效果好于對整體和YES類的。當決策樹達到380以后，各類錯判率基本保持穩定。所以本例中參數 ntree 可設置為380。

下面的圖為使用 margin 函數考察處于分類邊界附近的點的錯判情況。該函數以差的升序返回所有觀測的比率差。其中，比率差近似等于 0 的觀測紅色類（NO類）居多，多藍類（YES類）的預測錯誤較多。

head(treesize(rFM))#瀏覽各個樹的葉節點個數
head(getTree(rfobj=rFM,k=1,labelVar=TRUE))#提取第1顆樹的部分信息

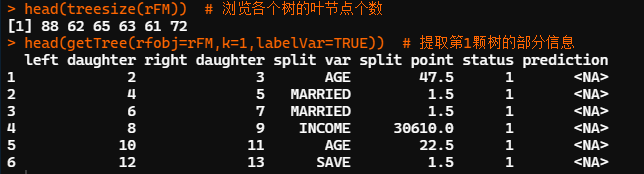
treesize函數可用于顯示隨機森林中各決策樹的大小。treesize(隨機森林結果對象名, terminal = TRUE/FALSE)，參數 terminal 取 TRUE 時僅統計決策樹的葉節點個數，取 FALSE 表示統計所有節點的個數。

本例中，第 1 顆決策樹包含 88 個葉節點。可利用 getTree 函數抽取隨機森林中的某顆樹并瀏覽其結構。

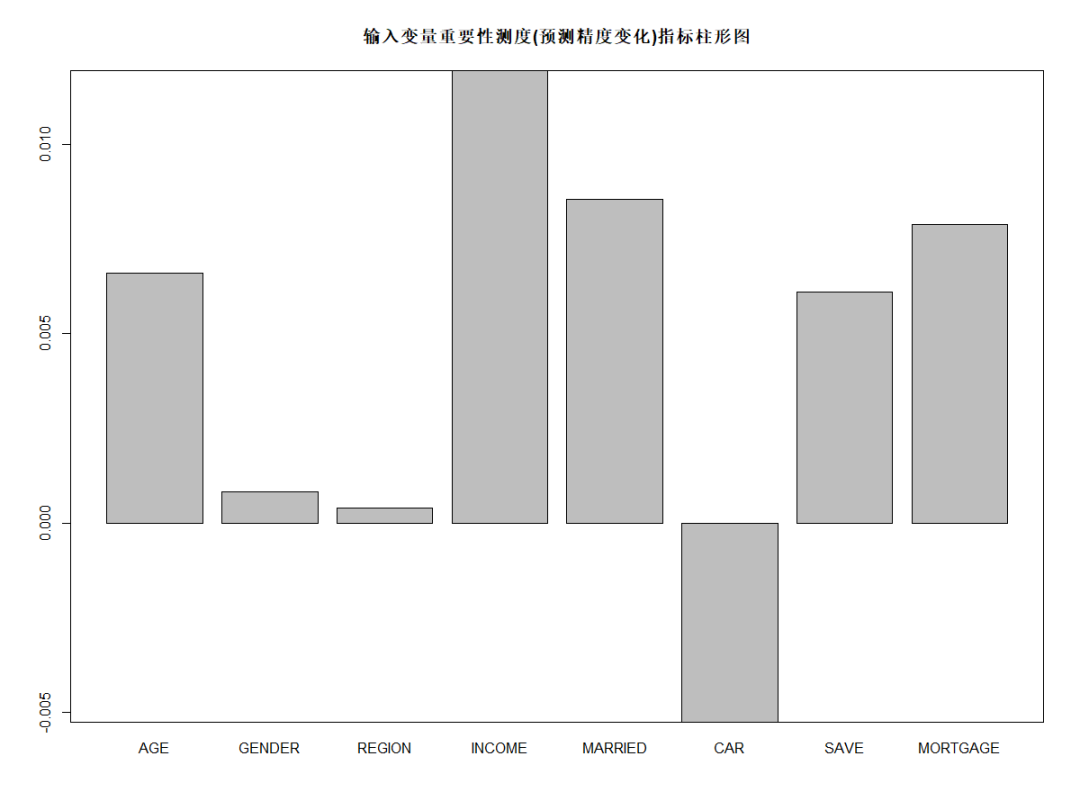
barplot(rFM$importance[,3],
main="輸入變量重要性測度(預測精度變化)指標柱形圖")
box()

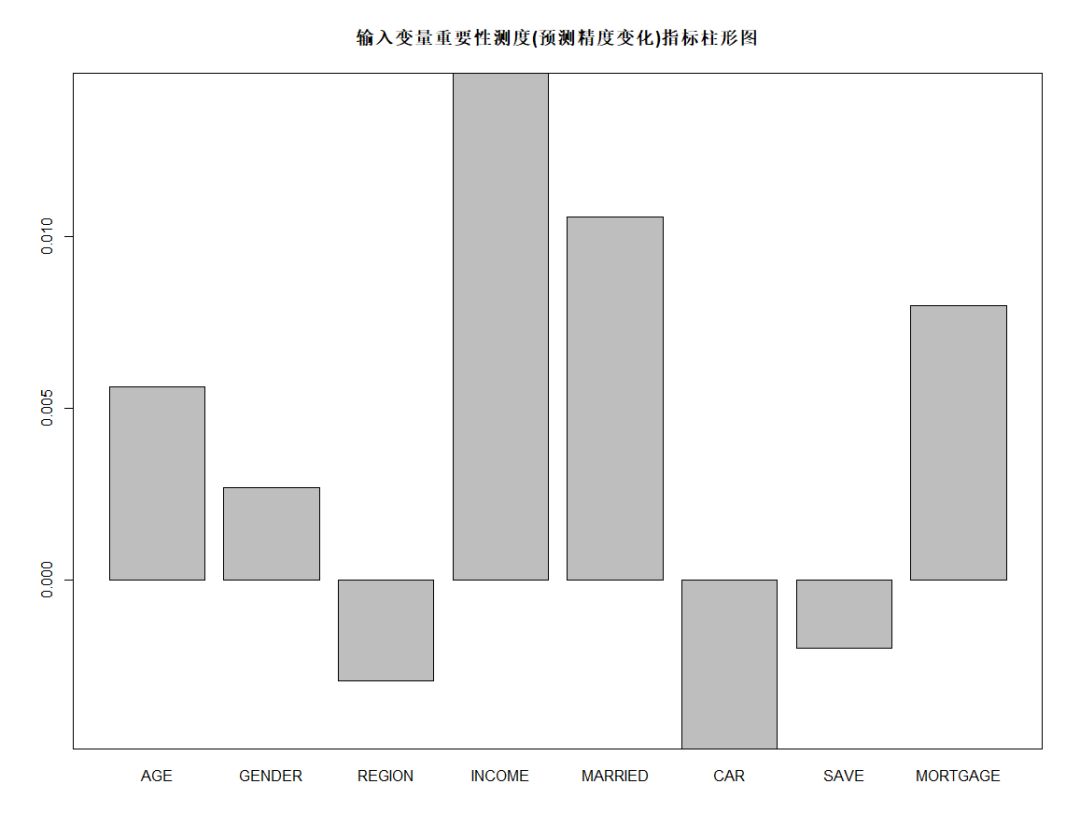
可調用randomForest包中的importance函數，importance(隨機森林結果對象名, type=類型編號)。

importance(rFM,type=1)

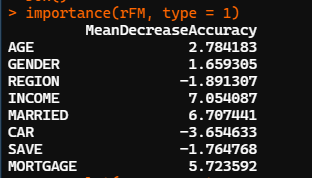
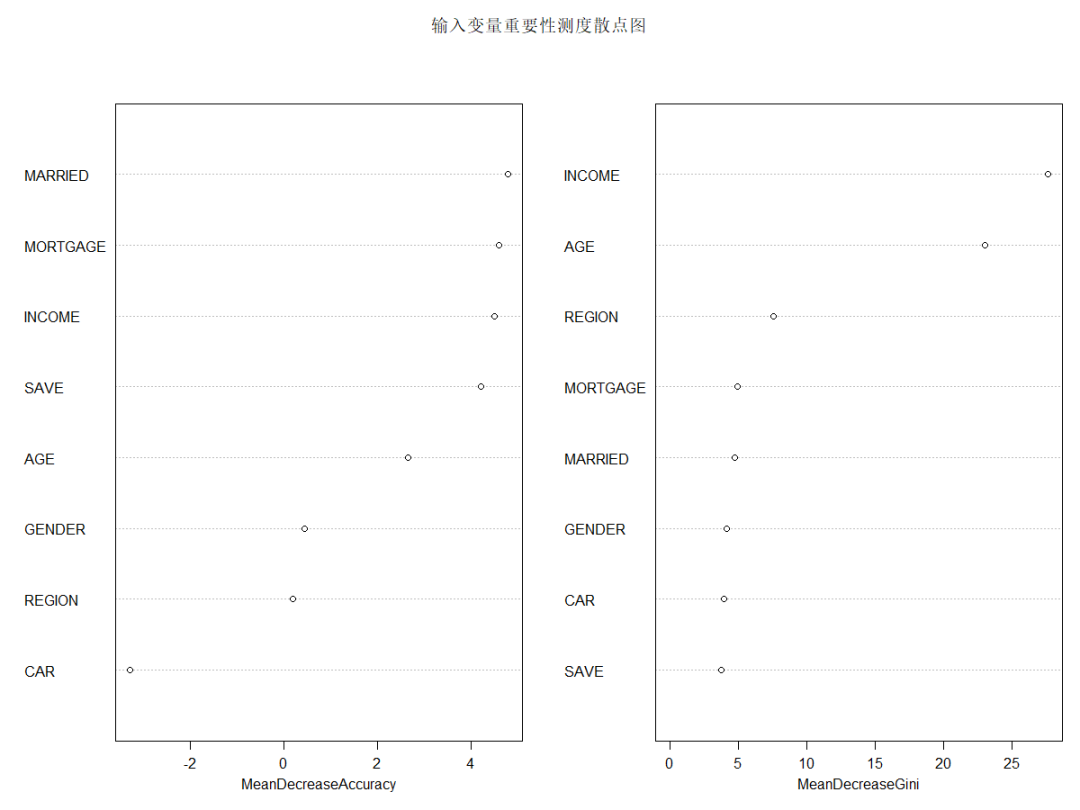
varImpPlot(x=rFM,sort=TRUE,n.var=nrow(rFM$importance),main="輸入變量重要性測度散點圖")

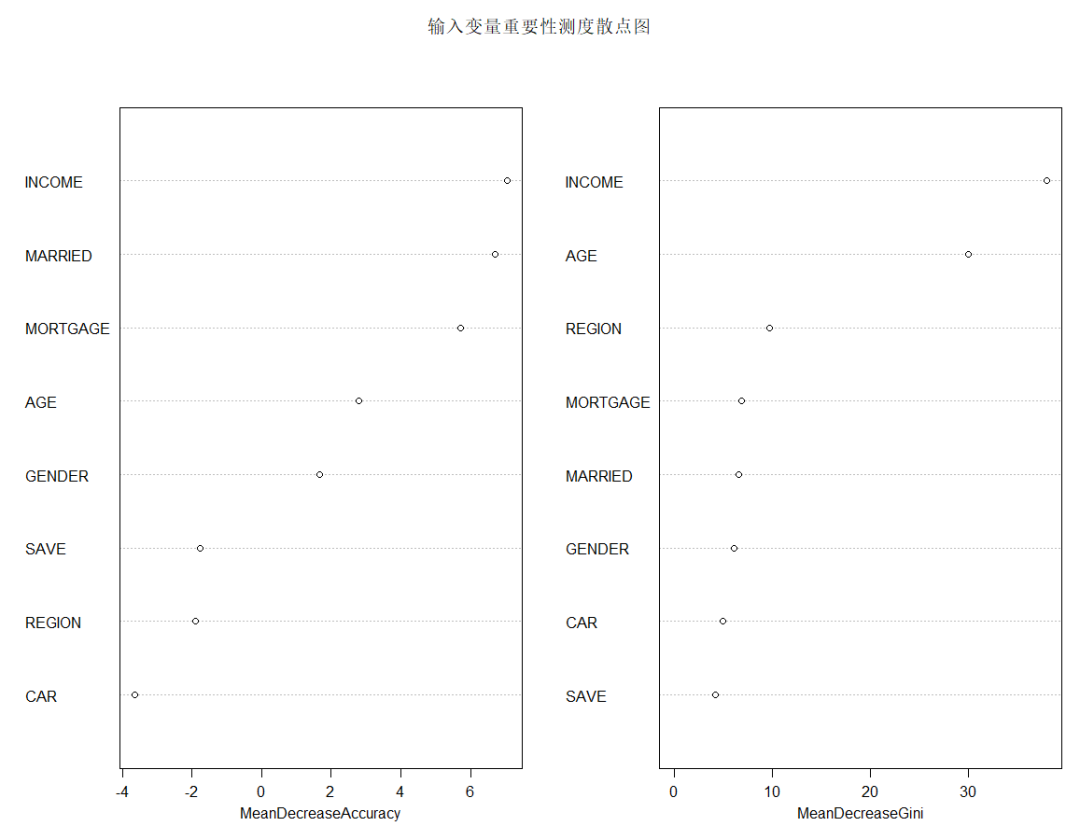
由上圖可知，從對輸出變量預測精度影響的角度看，收入、是否有債務、婚姻狀況較為重要；從對輸出變量異質性下降程度看，收入、年齡和居住地較為重要，即收入不同，年齡不同，居住地不同的人群對快遞郵件的反應有較大差異。

練習

將上述數據分成70%訓練集，訓練隨機森林模型，并對剩下30%預測，計算預測準確率。并且評價變量重要性。

library(randomForest)
MailShot<-read.table(file="郵件營銷數據.txt",?header?=?T)
MailShot<-MailShot[,-1]
MailShot$MAILSHOT?<-?as.factor(MailShot$MAILSHOT)
nrow(MailShot)
n?<-?sample(c(1:300),?300*0.70,?replace?=?F)
MailShot_train?<-?MailShot[n,]
MailShot_test?<-?MailShot[-n,]

set.seed(12345)
(rFM<-randomForest(MAILSHOT~.,data=MailShot_train,importance=TRUE,proximity=TRUE))
head(rFM$votes)??#?各觀測的各類別預測概率
head(rFM$oob.times)??#?各觀測作為?OOB?的次數
DrawL<-par(mfrow=c(2,1),mar=c(5,5,3,1))
plot(rFM,main="隨機森林的OOB錯判率和決策樹顆數")
plot(margin(rFM),type="h",main="邊界點探測",
?????xlab="觀測序列",ylab="比率差")?#?探測邊界點
par(DrawL)

Fit<-predict(rFM,MailShot_test)??#?隨機森林對測試數據做預測
ConfM<-table(MailShot_test$MAILSHOT,Fit)??#?隨機森林對測試數據做預測的混淆矩陣
(E<-(sum(ConfM)-sum(diag(ConfM)))/sum(ConfM))??#?隨機森林的整體錯判率
#?0.4222222

審核編輯：郭婷