為什么要讀書?
為什么要讀書?
書本里,有幾千年的哲學觀點、有幾百年的科學規律、幾十年的技術總結。
多讀書,可以幫助看明白這個世界,看明白人。
時域、頻域、s域、z域
大學《信號與系統》講了四種域:時域、頻域、s域、z域。
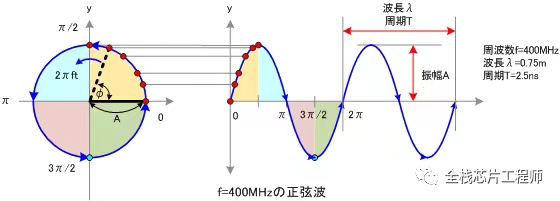
本質上,頻域、s域、z域,都是從時域變換到頻域。
時域:
連續信號:x(t)
離散信號:x[n]
頻域:
連續信號:X(jw)
離散信號:X(e^jw)
轉換關系
時域與頻域:傅里葉變換
時域與s域:拉普拉斯變化
時域與z域:z變換
頻域與s域:jw = s
頻域與z域:e^jw = z
為何傅里葉變換?
為什么時域要變化到頻域?
當信號從時域變換到頻域后。可以觀察到很多時域看不到的現象。特別是很多在時域看似不可能的數學操作,在頻域反而so easy!
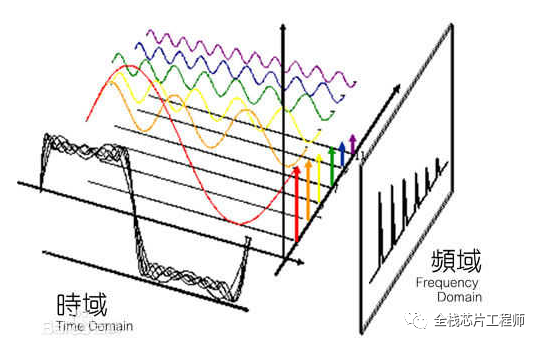
比如,紙上動筆畫一個sin(x)函數波形,很簡單!
那讓你畫一個sin(3x)+sin(5x)波形呢?無從動筆?
那給你一個sin(3x)+sin(5x)波形,讓你畫一個sin(5x)波形呢?
在頻域,sin(3x)+sin(5x)就兩條豎線!剔除sin(5x)是不是很簡單。
從一條曲線中,去除一些特性頻率成分,就是信號處理中的濾波。
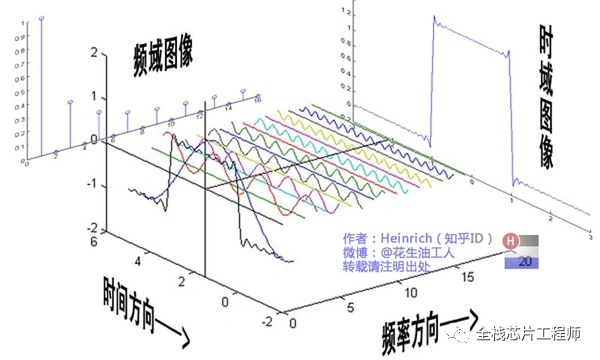
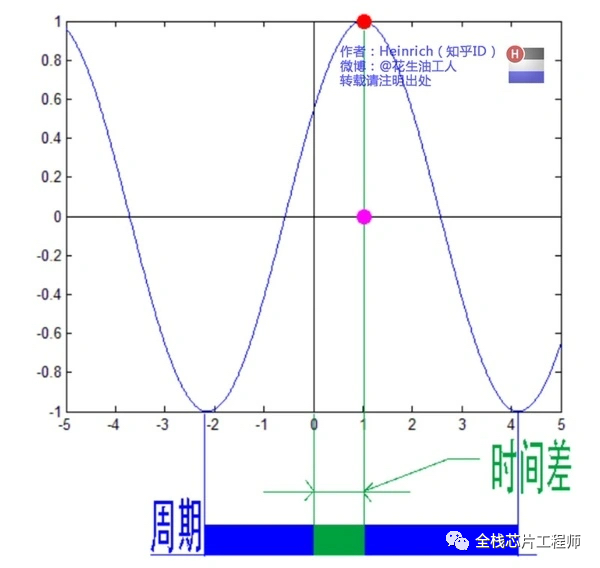
頻譜只代表每一個正弦波的振幅,沒有相位信息。相位如何表示?
鑒于正弦波是周期的,我們用下圖紅色點來標記離頻率軸最近的波峰:
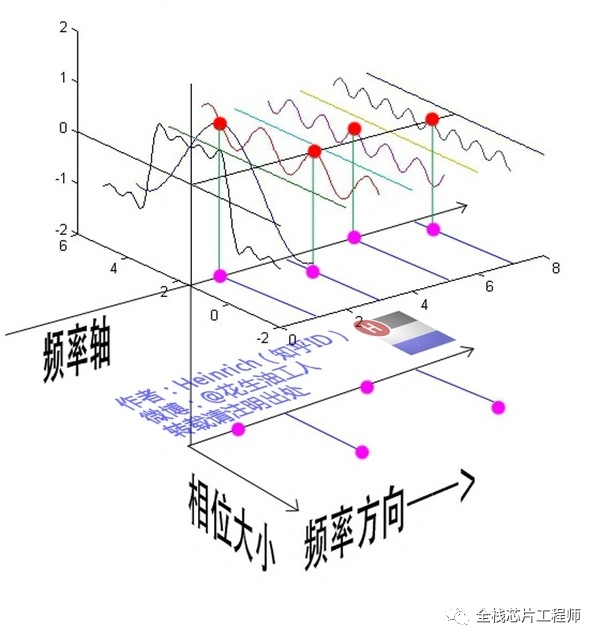
為了看清楚,我們將紅色點往下平面投影成粉色點,粉色點與頻率軸的距離,這個距離占正弦波的周期的百分比,乘以360°就是相位。
為何要拉普拉斯變換?
為何要拉普拉斯變換?
傅里葉變化只能對能量有限的信號進行變換(也就是可以收斂的信號),無法對能量無限的信號進行變換(無法收斂),因此,拉普拉斯應運而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進行時頻變換。
換而言之,傅里葉變換不能分析系統的穩定性,而拉普拉斯變換轉成s域就能分析系統的穩定性。
很多曲線,都可以用這些不同頻率,連續旋轉的圓,通過線性疊加得到,而傅里葉定律,就是對這個結論的數學描述,傅里葉定律說:只要一個函數滿足如狄利赫里條件,都能分解為復指數函數之和,哪怕是如拉格朗日提到的帶有棱角的方波函數。狄利赫里條件為:

傅里葉變換有一個很大局限性,那就是信號必須滿足狄利赫里條件才行,特別是那個絕對可積的條件,一下子就攔截掉了一大批函數。比如函數f(t)=t^2就無法進行傅里葉變換。這點難度當然拿不到聰明的數學家們,他們想到了一個絕佳的主意:把不滿足絕對的可積的函數乘以一個快速衰減的函數,這樣在趨于正無窮時原函數也衰減到零了,從而滿足絕對可積。
數學描述是:
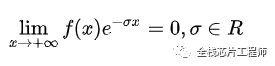

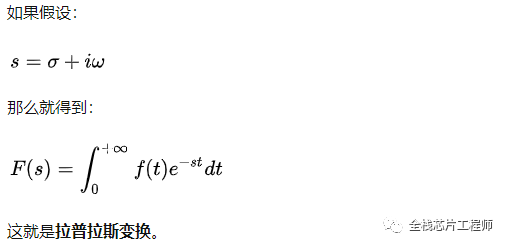
先上圖,我們下文講零極點穩定性問題。
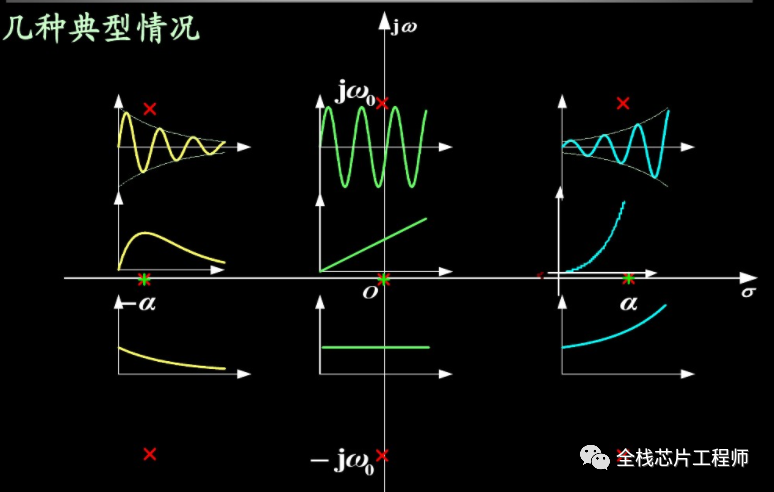
零點、極點分析
1、零點
零點:使系統傳遞函數G(s)為0的s的值,其中s為復數。比如:
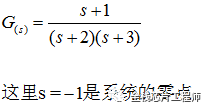
s=-1是零點。
2、極點
極點:使系統傳遞函數G(s)分母為0的s的值,其中s為復數。比如:
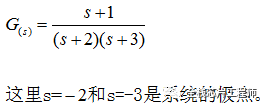
s=-2、s=-3是極點。
為何Z變換?
我們知道,傅里葉變換公示如下:
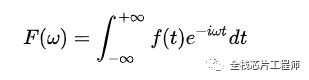
在函數收斂情況下,才可傅里葉變換,不收斂則乘以一個衰減函數形成拉普拉斯變換。
同樣的,離散周期信號的傅里葉級數為:
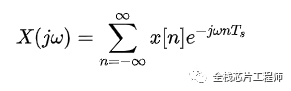

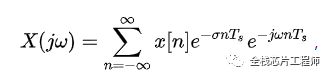
進一步化簡:
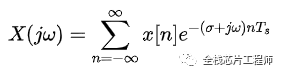
令:
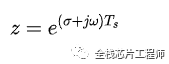
則DFT的表達式變為:這就是Z變換!!!
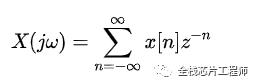
精采絕倫嗎?繼續high
由連續函數*衰減函數的傅里葉變換,即拉普拉斯變換,我們假定了:
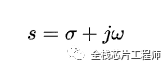
由離散函數*衰減函數的傅里葉變換,即Z變換,我們假定了:
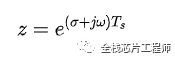
也就是說,z域和s域有如下關系:
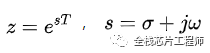


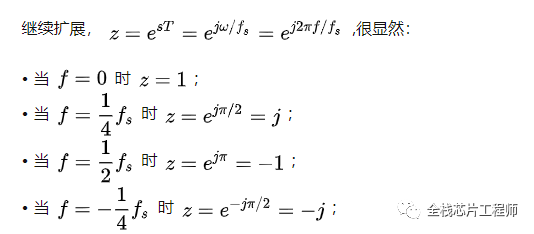
我們知道在s域上,虛軸上不同的點對應不同的頻率,而z域上單位圓與s域虛軸對應,可見,z域單位圓上不同的點,代表了不同的頻率。
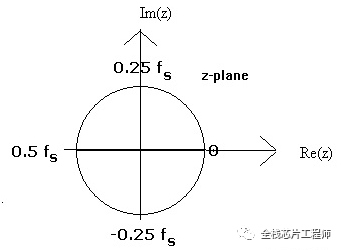
對于z域的傳遞函數的零極點,也有和s域零極點類似的結論:
規律1:如果在單位圓上有零點,則在零點所對應的頻率上幅值響應為零;
規律2:對于不在單位圓上的零點,在單位圓上離零點最近的點對應的頻率上幅值響應最小。
規律3:對于在單位圓內部的極點,在單位圓上離極點最近的點對應的頻率上幅值響應最大。
規律4:如果極點和零點重合,對系統的頻率響應沒有影響。
零、極點影響頻率響應
例子1:
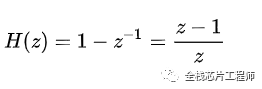
對于這個系統,在z=0有一個極點,在z=1時有一個零點。零、極點分布如下:
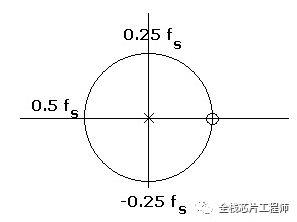
其中o表示零點,x表示極點。從z=1也就是單位圓上角度為零(也是頻率為零)的點開始,此處z=1有一個零點,根據規律1,顯然在頻率為零時系統響應為零。
順著單位圓沿逆時針方向旋轉,我們離零點越來越遠,零點的影響也越來越小,因此幅值響應會逐漸增大。當我們到達z=-1 ,也就是頻率為1/2fs時,此時離零點最遠,因此響應會達到一個最大值,當頻率繼續增大時,由于離零點又開始接近了,幅值響應又開始變小。
極點正好位于圓心位置,也就是說所有頻率段離極點的距離都一樣,因此可以認為都沒影響。
用freqz函數將系統的頻響畫出來,如下圖,這個系統本質上是一個高通濾波器。
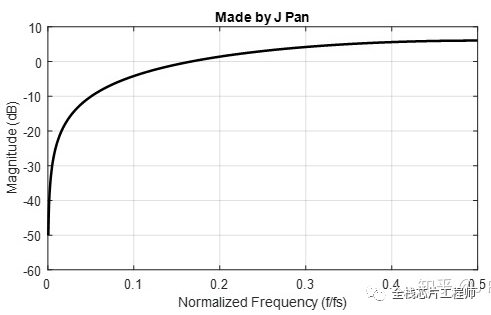
這個系統轉換到時域:

是不是很驚喜,這本質就是一個差分,低頻信號被過濾,高頻信號通過。
這一個差分,對應連續系統的微分。我們知道微分對應的是傳遞函數是s,穩態時為s=jw,這顯然是一個高通濾波器。
審核編輯 :李倩
-
濾波器
+關注
關注
160文章
7727瀏覽量
177671 -
傅里葉
+關注
關注
0文章
59瀏覽量
20447 -
拉普拉斯
+關注
關注
0文章
35瀏覽量
9645
原文標題:【剖析】傅里葉變換、拉普拉斯變換、Z變換
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
傅里葉變換的基本性質和定理
經典傅里葉變換與快速傅里葉變換的區別
傅里葉變換與圖像處理技術的區別
傅里葉變換在信號處理中的應用
傅里葉變換的數學原理
先進產能設備提供商拉普拉斯科創板上市
拉普拉斯變換的作用及意義
數字信號處理三大變換關系包括什么
拉普拉斯科創板IPO過會
傅里葉變換和拉普拉斯變換的關系是什么
傅里葉變換的應用 傅里葉變換的性質公式
什么是傅里葉變換和逆變換?為什么要用傅里葉變換?





 傅里葉變換、拉普拉斯變換、Z變換剖析
傅里葉變換、拉普拉斯變換、Z變換剖析











評論