這是翻譯自1988年《美國數學月刊》所刊登的關于《高斯，蘭登，拉馬努金，算術幾何平均數，橢圓，和女士日志》的相關科普文章，文中刪減了關于拉馬努金，橢圓和的部分，所以標題也簡化了。限于譯者水平，文中有不少翻譯不恰當的地方，希望讀者提出寶貴意見，批評指正。如果想要了解相關可以參考附錄。

本文主要為了使大家了解橢圓積分的數值計算，重點是蘭登變換(Landen's Transformation)的內容。

Virtue and sense, with female-softness join'd (All that subdues and captivates mankind!) In Britain's matchless fair resplendent shine; They rule Love's empire by a right divine: Justly their charms the astonished WorId admires, Whom Royal Charlotte's bright example fires.

美德和理智，與女性的溫柔結合在一起（征服和吸引人類的一切！）在英國無與倫比的光輝中；她們以一位正義的神來統治愛的帝國：正是她們的魅力讓世界驚嘆不已，皇家夏洛特的光輝榜樣激發了她們。

1. 前言

算術幾何平均數(AGM, Arithmetic-Geometric Mean)是由拉格朗日(Lagrange)首先發現的，幾年后高斯(Gauss)在他十幾歲的時候重新發現了它。然而，高斯的主要貢獻，包括優雅的積分表示，是在大約7至9年后所做出的。那么，本文的第一個目的是解釋算術幾何平均數并描述它的一些主要性質，其中主要是高斯的貢獻。

算術幾何平均數由于它的快速收斂性，其在過去十年中被大量用于快速機器計算。因此，本文的第二個目的是描述它在計算中的作用。我們還強調算術幾何平均數具有更廣泛的應用，例如，用于計算基本函數如、、和。有興趣的讀者應該進一步參考這里引用的幾個參考文獻，尤其是Brent的論文[14]和Borweins的書[13]。

算術幾何平均數的確定與橢圓周長的計算密切相關。自開普勒(Kepler)和歐拉(Euler)時代以來，已經發現了幾個近似公式來計算周長。得出這種近似關系的主要動機顯然是希望準確計算行星的橢圓軌道。因此，本文的第三個目的是描述算術幾何平均數與橢圓周長之間的聯系，并考察了文獻中許多近似公式，其中最準確的要歸功于拉馬努金(Ramanujan)，他還發現了一些非常不尋常和奇特的橢圓周長近似公式，后者的結果可以在他的筆記本中找到，并且從未發表過，因此我們將特別介紹了這些近似公式。

英國數學家約翰·蘭登(John Landen)也對這一思想做出了貢獻。在算術幾何平均數和橢圓周長確定的研究中，出現了他最重要的數學貢獻，現在稱為蘭登變換(Landen's transformation)。文獻中存在許多關于蘭登變換的非常重要且看似無關的變體。因此，本文的第四個目的是描述蘭登變換的幾個公式，并提供這位鮮為人知的數學家一個簡短的傳記。

幾年來，蘭登幾乎只在《女士日志》(The Ladies Diary)上發表文章。這是歷史上第一個定期出版的期刊，其中包含專門討論數學問題及其解決方案的部分。由于《月刊》(The MONTHLY, 譯注：本文的刊登刊物)的一個重要特點源于《女士日志》，因此在本文中對《女士日志》進行簡要描述似乎具有雙重意義。

2. 高斯和算術幾何平均數

正如我們之前提到的，算術幾何平均數首先在1784-85年出版的拉格朗日[30]的回憶錄中提出。然而，在1816年4月16日給朋友舒馬赫（H. C. Schumacher，譯注: 丹麥天文學家）的一封信中，高斯透露說，他在1791年14歲時獨立發現了算術幾何平均數，大約在22或23歲時，高斯寫了一篇長篇論文[23]描述了他在算術幾何平均數方面的許多發現。然而，與高斯的許多其他作品一樣，這部作品直到他去世后才出版。因此，高斯的基礎論文直到1866年才出現，當時高斯全集的編輯謝林(Ernst Christian Julius Schering)將該論文作為高斯遺稿的一部分發表。高斯顯然非常重視他對算術幾何平均數的發現，因為他日記中的一些條目都與算術幾何平均數有關，特別是從1799年到1800年的，其中一些條目非常模糊，我們可能仍然不知道高斯發現的關于算術幾何平均數的所有內容。（有關高斯日記和評論的英文翻譯，請參閱J. J. Gray的論文[24]）

到目前為止，讀者可能已經迫不及待地想了解算術幾何平均數以及年輕的高斯發現了什么。

和表示的正數，構造算術平均數序列和幾何平均數序列如下：

高斯在[23]給出了四個數值例子，我們復制了其中一個，令和，然后有：

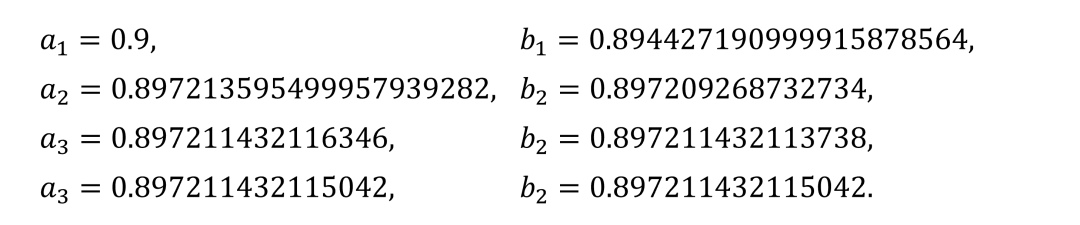
（顯然，高斯并沒有吝嗇他的數值計算）從這個例子中可以看出，和收斂到相同的極限，而且這種收斂非常迅速，我們現在對此進行證明，注意到如此等等。因此，是遞增且有界的，是遞減且有界的。每個序列因此而收斂，由初等代數計算得到按上述公式迭代這個過程，我們推出當趨向于時它趨向于，因此，和收斂到相同的極限，我們用表示這個收斂的極限值，根據定義是和的算術幾何平均數。

為了更加定量的衡量收斂速度，首先定義

其中和，注意到因此，趨向于二次方，或者收斂是二階的。更一般地，假設收斂到并假設存在常數和使得那么我們說收斂是階的。

高斯的論文[23]中最重要的定理可能是的以下表示，我們為此提供了高斯的巧妙證明過程

定理：

讓，并定義然后積分稱為第一類完全橢圓積分(the complete elliptic integral of the first kind)。注意在的定義中，可以被代替。

在證明定理之前，我們對其進行重新表述，定義很容易看出其中因為

對于任何常數，它滿足上面的，可以立即由定理得到以下表述

定理：

令，有證:

顯然，是的偶函數，高斯然后假設現在進行替換，由(4)式可知代入(5)，我們發現顯然，，對二項式級數中展開，并令兩邊的同冪系數相等，我們最終發現這里我們介紹如下記號推導(6)的完整細節可以在高斯的論文[23, pp.367-369]中可以找到。

我們現在必須用來確定(6)中的級數，在二項式級數中展開的被積函數并逐項積分，我們發現結合(6)和(8)，我們完成了高斯定理的證明。

Newman在[39]中給出了定理的另一個簡短而優雅的證明，并由J. M.和P. B. Borwein在參考中[10]作了概述。

關于高斯對算術幾何平均值的許多貢獻，請參見Cox的論文[18]。我們將在第5節繼續討論高斯的一些發現。

3. 蘭登和女士日志

我們接下來簡述定理(或定理)的另一個證明，這主要歸功于18世紀的英國數學家約翰·蘭登(John Landen)。

證明2：

雖然基本思想源于蘭登，但我們將要描述的迭代過程顯然是由若干年后的勒讓德(Legendre)[33, pp. 79-83]提出的，為簡潔起見，設其中由(1)定義，在第一類完全橢圓積分(2)中，代入這稱為蘭登變換，經過大量的計算，我們發現在次迭代后，得到由于通過(1)和(9)，，我們看到(11)簡化為現在我們讓趨向于，由于趨向于而趨向于，我們得出結論蘭登變換(10)是由他在1771年發表的一篇論文[31]中提出的，并在他1775年發表的最著名的論文[32]中以更完善的形式呈現。蘭登變換存在多個版本，蘭登變換通常表示為橢圓函數理論中兩個微分之間的相等關系[17]，[37]。米塔格-萊弗勒(Mittag-Leffler)指出了蘭登變換的重要性，他在對橢圓函數理論的非常敏銳的調查[37, p. 291]中評論說，“歐拉加法定理和蘭登與拉格朗日變換定理是橢圓函數理論在1786年被勒讓德重新考慮時所擁有的兩個基本思想。”

在第4節中，我們將證明以下定理，通常稱為第一類完全橢圓積分的蘭登變換。

定理.

如果，那么事實上，定理是以下當時更一般公式的特例。如果，那么這被稱為第一類不完全橢圓積分的蘭登變換。

為了描述蘭登變換的另一種形式，我們引入高斯超幾何級數(Gauss's hypergeometric series)其中、和表示任意復數，由(7)定義，然后蘭登對超幾何級數的變換是定理和意味著如下的特殊情況因此，看似不起眼的“變量變化”(10)具有許多重要的難以意料的結果。事實上，蘭登本人顯然從未意識到他想法的重要性。

無疑大多數讀者都不知道蘭登，因此在這里給出一個簡短的傳記似乎是合適的。他出生于1719年，根據大英百科全書[20]，“他過著非常隱逸的生活，對社會幾乎一無所知；當他真的融入其中時，他的教條主義和好斗性使他不被接納”。1762年，他被任命為Earl Fitzwilliam的土地代理人，直到1790年他去世的前兩年。

作為一名數學家，蘭登主要是一名分析師和幾何學家。他的大部分重要作品都是在他職業生涯的后期發表的。其中包括上述論文和數學回憶錄，分別于1780年和1789年出版。多年來，蘭登為《女士日志》貢獻了許多問題和解決方案。從1743年到1749年，他一共提出了11個問題，并發表了13個問題的解決方案。然而，Leybourn在[34]中透露，《女士日志》的撰稿人經常使用別名，特別是，蘭登使用了化名Sir Stately Stiff、Peter Walton、Waltoniensis、C. Bumpkin 和Peter Puzzlem，他們共同提出了10個問題并回答了17個問題。Leybourn在[34]中將 1704-1816年《女士日志》中的問題和解決方案匯編成四卷。特別有價值的是他的學科分類和貢獻者指數。(1704-1760年的問題和解決方案之前已被其他人收集在1774年的一卷中[50]。)

1704年首次出版的一年一度的《女士日志》顯然在英國很受歡迎，年發行量達數千份。女士日志“主要是為的娛樂和指導男女平等而設計的”。它包含“藝術和科學新的進步，以及許多有趣的細節……用于公平的性別對待。”封面上有一首獻給在位女王的詩，通常每年幾乎沒有變化。我們的論文從1776年的一首詩開始，它深深地向喬治三世國王的摯愛致敬。除其他外，《女士日志》包含“重大事件年表”、王室出生日期、謎團以及對前一年謎團的答案，謎題和答案通常被設置為詩句。

《女士日志》的大部分內容專門用于解決上一期提出的數學問題。盡管該期刊的名稱如此，但女性的貢獻者寥寥無幾。Leybourn的簡編[34]總共列出了913名貢獻者，其中32名是女性。因為提議者和求解者確實偶爾會使用Plus Minus、Mathematicus、Amicus、Archimedes、Diophantoides等筆名以及上述蘭登的別名，所以女性貢獻者的數量可能略高一些。...幾何問題很流行，但是嚴謹性很差，如下是1783年的一個例子，令證明。1784年，約瑟夫法蘭西(Joseph French)提供了以下“優雅”的解決方案，我們看到因此，。

那些希望了解更多關于蘭登作品的讀者可以參考Watson的文章“侯爵和土地代理人”[52]（The Marquis and the Land-agent）。想要了解更多《女士日志》數學內容的讀者，一定要查閱Leybourn的簡編[34]。(美國只有少數圖書館擁有《女士日志》的副本。伊利諾伊大學圖書館擁有相當詳盡的館藏，盡管在1774年之前存在一些空白。T. Perl在[43]中已詳細描述了《女士日志》重點是女性的貢獻，并分析了日志中女性數學教育的積極和消極社會學因素。有關《女士日志》和其他晦澀難懂的英語數學期刊的更多歷史信息，請參閱Archibald的論文[2])

4. 伊沃里和蘭登變換

1796年，伊沃里(J. Ivory, 1765-1842)[25]發表了橢圓周長的新公式。一個非常相似的證明建立了定理2，這是上一節中討論的蘭登變換的另一個版本。

在證明定理之前，我們注意到它也暗示了定理的一個新版本。

定理.

如果，那么定理也來自定理；讓并利用(4)。

定理的證明:

使用的定義(2)，采用二項式級數，并交換下面的求和和積分的順序，由(8)，我們發現證畢。

伊沃里的論文[25]建立了定理2的類似公式，具有一個不同尋常的特點，即它以伊沃里在提交論文時發送給編輯John Playfair的“求職信”開頭！在這封信中，伊沃里告訴Playfair是什么導致了他的發現。顯然，編輯認為將伊沃里的信作為論文的序言發表是公平的，這封信內容如下：

如您所知，我花了很多時間和精力研究與行星相互干擾有關的物理天文學部分，自然而然地，我被引導考慮解決公式的各種方法, 轉化為形式的無限級數。在這些研究過程中，我想到了一系列對…進行校正的方法，其簡單性和快速收斂性令人贊嘆。由于我認為它是新的，所以我將它發送給您，并附上一些關于剛才提到的公式演變的備注，如果您認為合適，您可以提交給皇家學會考慮。

詹姆斯·伊沃里

審核編輯 ：李倩