幾個世紀以來,數學一直依賴積分函數作為理解物理測量相互關系的輔助手段。例如,可以應用積分(或曲線下面積)函數來實現單位變換。可以對速度方程進行積分以推導出位移方程;或積分以推導出速度的加速度方程。類似地,可以通過集成函數來得出功度量,以產生活動的相對量度。我們大多數人,在某種程度上接觸過微積分,從純粹的數學意義上理解積分在方程中的應用。然而,將積分函數應用于波形代表了對該工具的更抽象的使用,這在微積分課程的一般課程中沒有涉及。這些應用知識只能通過經驗獲得,本應用筆記旨在傳達部分專業知識,以縮短學習曲線。
DATAQ Instruments的WinDaq數據采集系統的高級CODAS波形分析選項包含一個波形積分器,該積分器是本應用筆記的模型,體現了本文討論的波形積分的所有要素。
復位條件:波形積分的關鍵
波形積分器的目的是生成一個等長的波形,表示在預定積分周期內輸入信號曲線所限定的區域。積分周期表示累積面積重置為零并且面積累積與輸入信號的下一個點恢復的點。此重置活動對集成過程非常重要。在圖形意義上,它允許在不飽和的情況下生成任何長度的集成波形。在分析意義上,它允許將積分波形分解為有意義的段。
為了澄清這些要點,請考慮由汽車產生的速度波形,該波形被積分以得出位移。如果我們假設自動汽車總是沿同一方向行駛但速度不同,則產生的速度波形將始終高于或低于零(取決于行進方向),并且永遠不會越過零,因為這樣做意味著方向的改變。如果我們進一步假設汽車長時間高速行駛,那么很明顯,行駛的總距離會變得非常大。表示距離的速度積分越來越正(或負,取決于方向),直到發生飽和。當然,在數字系統中,波形可以根據最大距離進行縮放,但這樣做會抑制位移波形在較低位移值下(即自動開始移動時)的變化。
我們可以通過將復位條件應用于上述速度波形的積分來解決這些問題。如果我們應用基于時間的重置條件,例如 20 秒,則積分波形將每 20 秒重置一次。復位發生前波形的高度表示在 20 秒間隔內行進的總距離。由于我們已將位移波形分割為20秒的epoch,因此無需對波形進行大量縮放,并且位移波形的微小變化將明顯增強分析。
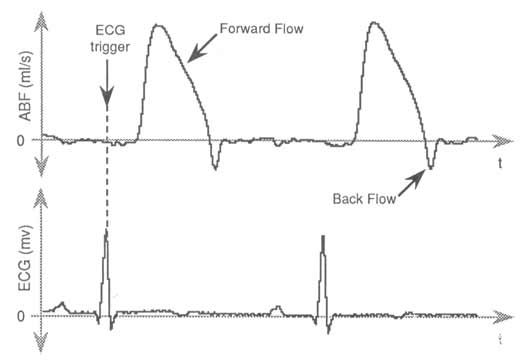
圖 1— 主動脈血流波形 (ABF) 的解剖結構包含正流和負流成分。ABF 與心電圖 (ECG) 信號同步;命令心臟跳動的電刺激。
讓我們考慮另一個基于行進距離的復位條件,并將波形積分器配置為每 1,000 英尺復位一次。由此產生的位移波形將在不同的時間重置,但在 1,000 英尺的行進距離后立即重置。同樣,由于我們對波形進行了分割,因此對縮放的需求大大減少,位移的任何波動都將很明顯。
我們可以擴展示例,以包括向前和向后行駛的自動移動,以及從速度波形得出向前和向后位移的需求。在這里,基于速度波形過零的復位條件可能是合適的。由于方向改變時必須達到零速度,因此此時積分器復位會產生向前和向后位移的分段視圖。
將復位條件應用于波形積分過程提供了靈活性,并且完全負責將積分函數的強大功能引入波形分析。波形積分通常采用幾種復位方法:作為過零、電平、時間和外部事件的函數。每個函數將在下面的示例中演示。
整流增強波形集成
在許多不同的應用中,通過將整流作為積分前的初步步驟來增強波形積分過程。考慮我們上面的例子,其中汽車向前和向后移動,產生的雙極性速度波形將被積分以產生位移。我們在這里使用了雙極標簽來描述由于汽車向前和向后移動而正負的速度信號。我們假設前進方向會產生正速度波形。
假設您只對推導正位移感興趣。雙極性速度波形可以在實際積分之前通過施加半波整流器進行預處理,該整流器僅將高于零速度的信號信息傳遞給積分器。同樣,如果您只關心負位移,則可以使用半波整流器僅將負向速度波形信息傳遞給積分器。總位移的度量可以通過在積分前對速度信號施加全波整流器(或絕對值)來得出。
波形整流形式的預處理增加了積分任務的分析靈活性。
主動脈血流:應用示例
無限數量的波形有資格用作波形積分的示例。在本應用筆記中,我們選擇了一種在醫學研究應用中遇到的波形,稱為主動脈血流(見圖1),因為它為波形積分提供了許多可能性。此波形的典型測量單位是毫升每秒 (ml/s)。正如其單位所暗示的那樣,主動脈血流(ABF)可以被認為是類似于英尺每秒或英里/小時的速度波形。積分時,ABF 波形根據公式(ml/s × s = ml)產生以毫升為單位的血容量測量值。
使用過零復位進行集成
高于 0 ml/s 的 ABF 波形區域表示前向音量;從心臟泵出的血液量。低于 0 ml/s 的波形區域表示背面音量;由于心臟瓣膜突然關閉并產生輕微的暫時性負壓而泵向心臟的血液量。ABF 的雙極性特性允許在積分之前應用整流器對波形進行預處理,以隔離正流和負流分量。此外,每當 ABF 越過零時,根據定義,速度方向就會發生變化,我們可以使用此特性來觸發積分復位。圖2顯示了如何應用整流器來隔離輸入ABF波形的正向和負向波形偏移,然后僅將這些段施加到積分器上。由此產生的積分波形提供了每個心臟周期中向前和向后泵送的血容量的測量值。圖2中每個積分輸出的復位條件在積分器軟件算法檢測到的ABF波形過零時立即發生。
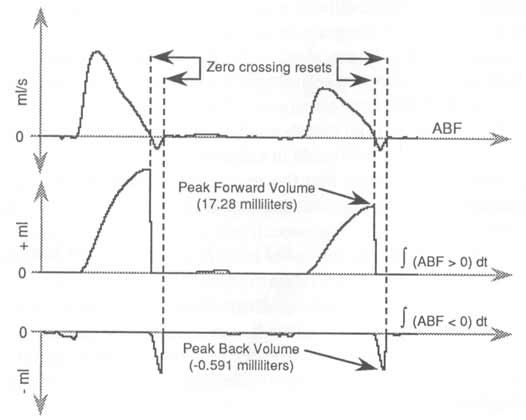
圖 2— 應用內置波形整流器功能可將 ABF 的正流和負流分量集成到單獨的正向和后向音量分量中。在本例中,ABF 波形的過零將重置積分。
使用電平、時間和外部復位進行集成
假設我們對 ABF 波形的興趣不是得出每個心臟周期泵出的血液量,而是得出心臟泵送給定數量的血液需要多長時間。過零復位在這里不適用。正如我們所看到的,這種方法僅適用于逐周期分析。為了實現我們的目標,必須應用一個完全不同的重置條件,稱為電平重置。給定所需積分波形電平,當達到該數量時,可以強制復位條件。重置條件之間的間隔表示達到指定水平所需的時間。轉到我們的示例 ABF 波形,指定 10 ml 的水平重置將導致積分器僅在泵送總共 10 ml 血液時才復位(見圖 3b)。ABF 的零交叉將被忽略。
時間重置與電平重置相反。電平復位派生出達到固定積分電平所需的時間,而時間復位派生積分波形在固定時間內達到的電平。轉到圖3c,啟用0.5秒的時間復位,產生43.3 ml的峰值積分值。與電平復位一樣,在時間復位操作期間,ABF波形的過零將被忽略。
最后,外部復位允許您將復位活動與輸入或任何其他通道上發生的外部事件同步。考慮空氣壓縮機的活塞以及測量活塞每次沖程期間施加的總功的需要。我們可以在氣缸頂部安裝一個壓力傳感器,在活塞的曲軸上安裝一個磁性拾音器,并通過數據采集系統獲取兩者的信號。使用另一個稱為峰值檢測器的高級CODAS軟件實用程序,我們可以峰值捕獲拾音器的波形,在每個拾音周期的峰值幅度處放置一個標記。相鄰標記之間的間隔表示活塞的一個周期,與曲軸轉速無關。然后,該“標記”波形成為積分壓力波形的同步復位條件,每次發生時都復位積分。結果是活塞施加的總功的逐周期真實度量。
回到我們的ABF波形,請記住它與心電圖(ECG)信號(見圖1)同步,該波形的峰值代表命令心臟跳動的電刺激。峰值捕獲ECG波形并使用所得標記物重置ABF積分,可以最準確地測量逐搏血容量(見圖4b)。
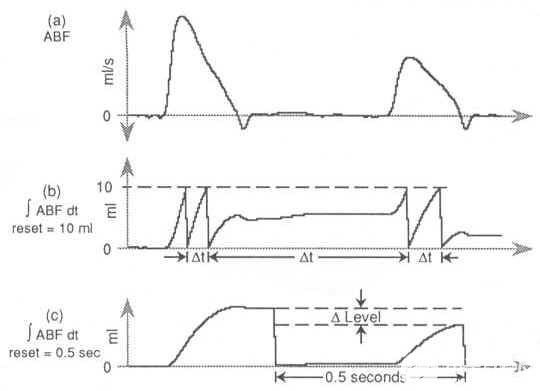
圖 3— 復位靈活性是有效波形集成的關鍵。信號ABF (a)產生(b)所示的波形,當積分值達到l 0 ml的水平時,該波形復位。積分在 (c) 所示波形中重置為時間(0.5 秒)的函數。
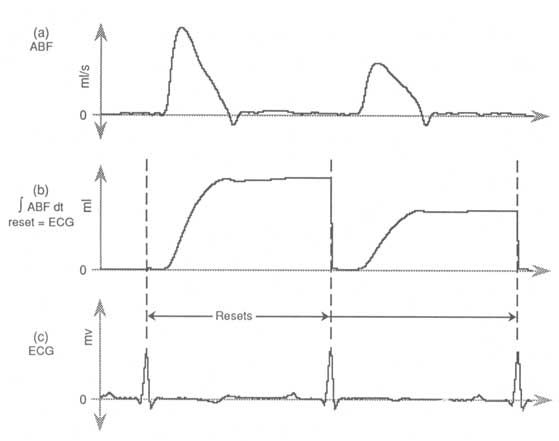
圖 4— 外部復位功能允許波形積分作為同步事件的函數復位。在這里,ABF (a) 的積分與 ECG 波形 (c) 同步發生,以產生 (b) 的積分結果,這是每個心臟周期泵血容量的最準確測量值。
其他波形積分問題
支持波形積分的軟件系統應該能夠以輸入信號的單位乘以秒為單位進行自動校準,因為校準積分波形可能是一項困難且耗時的任務。同樣,軟件應接受以輸出波形為單位的電平重置方法的參數,以避免困難的變換。例如,在積分以公里/秒為單位校準的速度波形之前,只需要“1000”公里的電平重置。最后,讀者必須理解,分別應用于復位條件和預積分調節的術語“過零”和“整流”是相對于輸入信號的零參考,而不是零伏或A-D計數。零校準測量單位很少與連接到A-D系統前端的零伏有關。輸入信號偏移幾乎總是存在的,所使用的數據采集系統應該能夠在A-D動態范圍內的任何點定義零點,并將其用作校準的零參考,以檢測波形過零并實現整流。
超越集成的分析
我們已經討論了一些可以應用于波形信息積分的強大技術。雖然查看積分結果和原始波形可以提供直觀上不明顯的見解,但可以通過提取逐周期峰值積分波形值并將其移植到電子表格或其他軟件包中進行進一步分析來應用進一步的數據分析。
審核編輯:郭婷
-
整流器
+關注
關注
28文章
1524瀏覽量
92349 -
積分器
+關注
關注
4文章
99瀏覽量
28421
發布評論請先 登錄
相關推薦
集成波形的壓電觸覺傳感器:DRV2605L-Q1和DRV2700

安達發|APS高級排程高級物料需求計劃

GD32E230C8T6高級定時器timer0無法正常輸出PWM波形的原因?
什么是任意波形發生器
任意波形發生器如何設置和調整輸出波形呢?
示波器顯示波形的原理詳解
任意波形發生器如何輸出電壓
泰克示波器如何捕捉瞬間波形?




 了解使用高級CODAS的波形集成
了解使用高級CODAS的波形集成










評論