背景

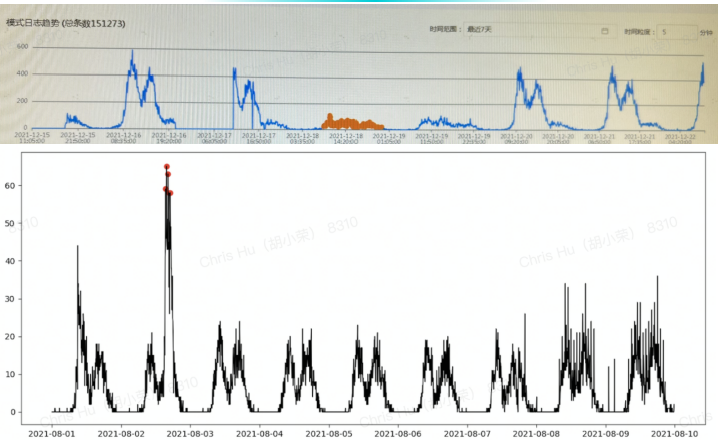
目前，日志異常檢測算法采用基于時間序列的方法檢測異常，具體為：日志結構化 -> 日志模式識別 -> 時間序列轉換 -> 異常檢測。異常檢測算法根據日志指標時序數據的周期性檢測出歷史新增、時段新增、時段突增、時段突降等多種異常。 然而，在實際中，日志指標時序數據并不都具有周期性，或具有其他分布特征，因此僅根據周期性進行異常檢測會導致誤報率高、準確率低等問題。因此如果在日志異常檢測之前，首先對日志指標時序數據進行分類，不同類型數據采用不同方法檢測異常，可以有效提高準確率，并降低誤報率。

日志指標序列的類型

日志指標序列分為時序數據與日志指標數據兩大類：

時序數據：包含平穩型、周期型、趨勢型、階躍型。

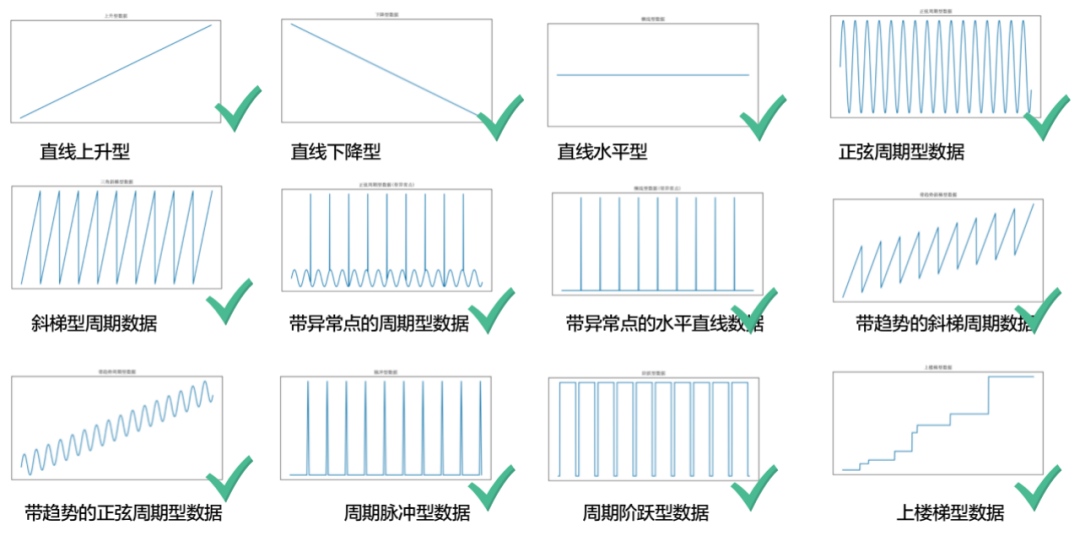
日志指標數據：包含周期型、非周期型。

時間序列分類算法

時間序列分類是一項在多個領域均有應用的通用任務，目標是利用標記好的訓練數據，確定一個時間序列屬于預先定義的哪一個類別。時間序列分類不同于常規分類問題，因為時序數據是具有順序屬性的序列。 時間序列分為傳統時間序列分類算法與基于深度學習的時間序列分類算法。傳統方法又根據算法采用的用于分類的特征類型不同，分為全局特征、局部特征、基于模型以及組合方法 4 大類。基于深度學習的時間序列算法分為生成式模型與判別式模型兩大類。本文主要對傳統時間序列分類算法進行介紹。

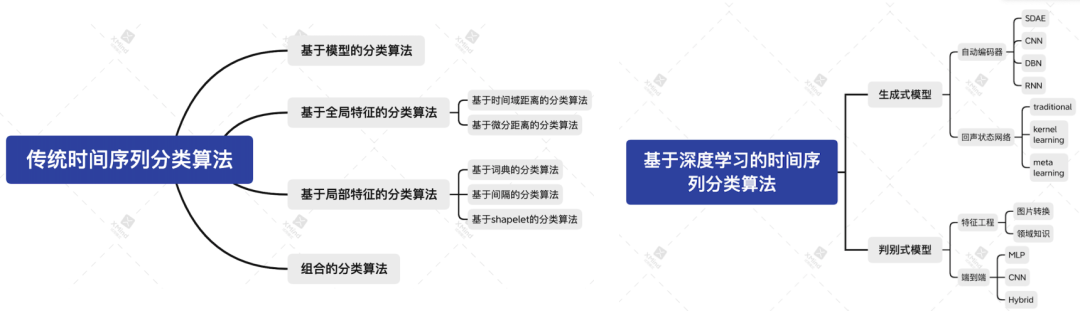
傳統時間序列分類算法

基于全局特征的分類算法

全局特征分類是將完整時間序列作為特征，計算時間序列間的相似性來進行分類。分類方法有通過計算不同序列之間距離的遠近來表達時間序列的相似性以及不同距離度量方法 + 1-NN（1 - 近鄰）。主要研究序列相似性的度量方法。

時間域距離

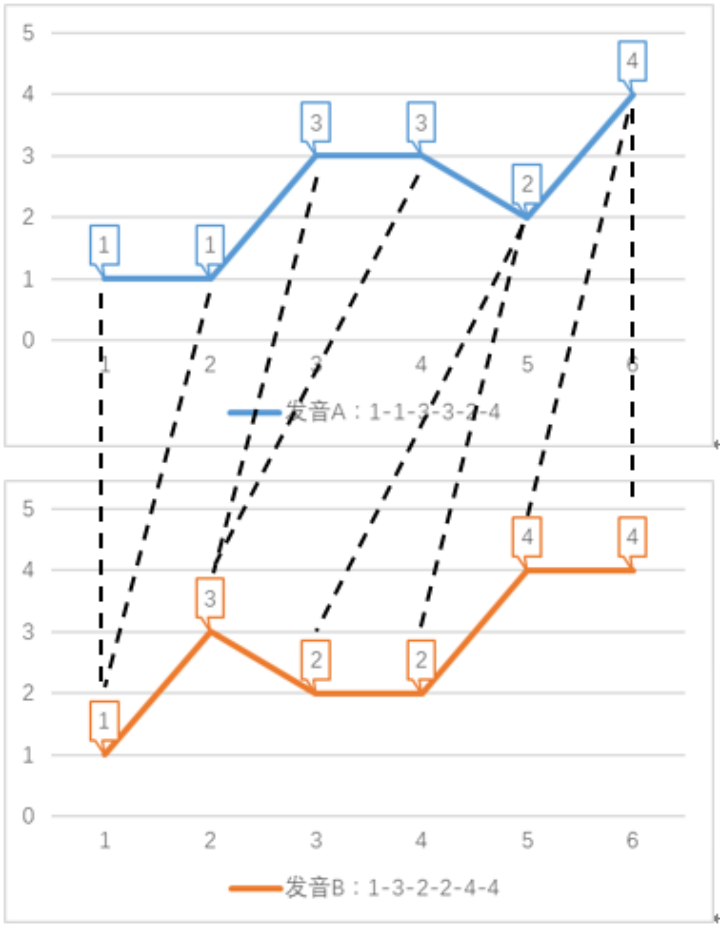
問題場景描述： 如下圖所示，問題場景是一個語音識別任務。該任務用數字表示音調高低，例如某個單詞發音的音調為 1-3-2-4。兩個人說同一單詞時，因為音節的發音拖長，會形成不同的發音序列 前半部分拖長，發音：1-1-3-3-2-4 后半部分拖長，發音：1-3-2-2-4-4 在采用傳統歐式距離，即點對點的方式計算發音序列距離時，距離之和如下：歐式距離 = |A (1)-B (1)| + |A (2)-B (2)| + |A (3)-B (3)| + |A (4)-B (4)| + |A (5)-B (5)| + |A (6)-B (6)| =6_x0001_

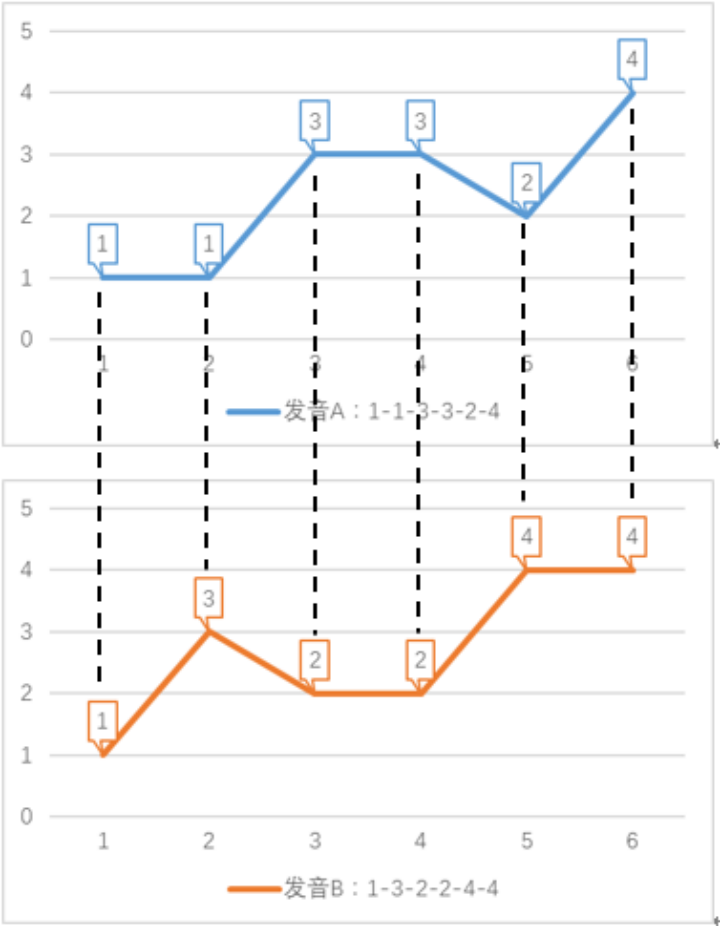
算法原理： 如果我們允許序列的點與另一序列的多個連續的點相對應（即，將這個點所代表的音調的發音時間延長），然后再計算對應點之間的距離之和，這就是 dtw 算法。dtw 算法允許序列某個時刻的點與另一序列多個連續時刻的點相對應，稱為時間規整（Time Warping）。如下圖所示，語音識別任務的 dtw 距離如下： dtw 距離 = |1-1| + |1-1| + |3-3| + |3-3| + |2-2| + |2-2| + |4-4| + |4-4| = 0 dtw 計算出的距離為 0，由此代表兩個單詞發音一致，與實際情況相符。

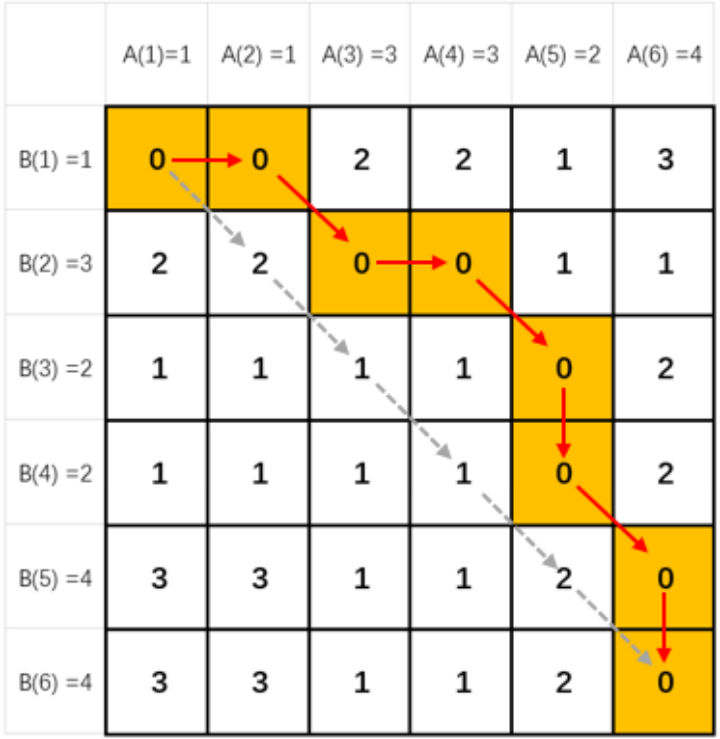
算法實現： dtw 算法實現包括計算兩個序列各點之間距離構成矩陣以及尋找一條從矩陣左上角到右下角的路徑，使得路徑上的元素和最小兩個主要步驟。距離矩陣如下圖所示，矩陣中每個元素的值為兩個序列對應點之間的距離。DTW 算法將計算兩個序列之間的距離，轉化為尋找一條從距離矩陣。左上角到右下角的路徑，使得路徑上的元素和最小。實現要點如下：

轉化為動態規劃的問題（DP）;

由于尋找所有路徑太耗時，需要添加路徑數量限制條件（可以等效為尋找矩陣橫縱坐標的差的允許范圍，即 warping window）。

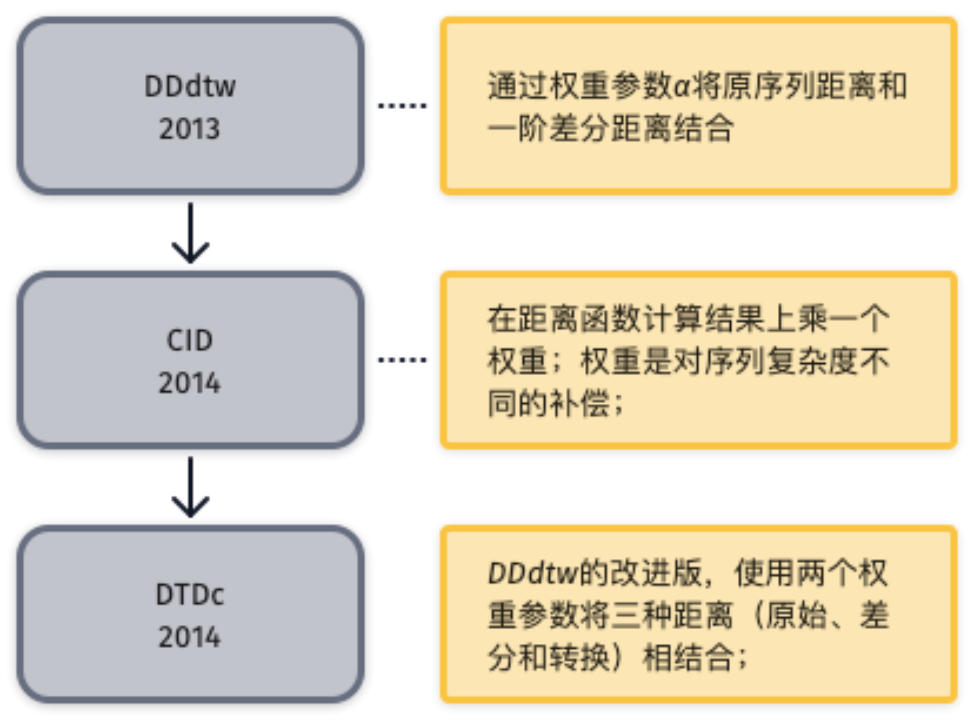
差分距離法

差分距離法是計算原始時間序列的一階微分，然后度量兩個時間序列的微分序列的距離，即微分距離。差分法將微分距離作為原始序列距離的補充，是最終距離計算函數的重要組成部分。 對于一個時間序列 t=（t1, t2, …,tm），其一階微分計算公式如（2-1）所示，二階微分計算公式如（2-2）所示，更高階的微分計算方式依次類推。差分距離法將位于時間域的原時間序列和位于差分域的一階差分序列相結合，提升分類效果。研究方向主要是如何將原序列和差分序列合理結合。

基于局部特征的分類算法

將單條時間序列中的一部分子序列作為特征，用于時間序列分類。主要有以下特點：

關鍵在于尋找能夠區分不同類的局部特征；

由于子序列更短，因此構建的分類器速度更快；

但由于需要尋找局部特征，需要一定的訓練時間。

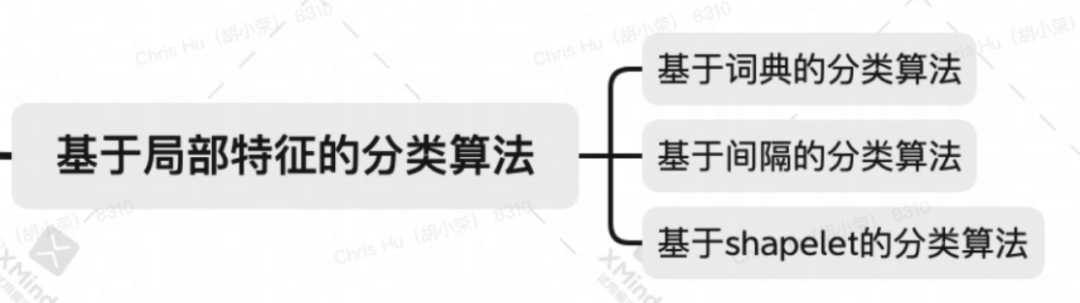
基于間隔（interval）的分類算法

基于間隔（interval）的分類算法分類方法是將時間序列劃分為幾個間隔，從每個間隔中提取特征。過程中需考慮以下關鍵問題：

需要找到最具有區分度特征的區間；

區間劃分方法很多，如果處理大量的候選區間；

如何在每個區間上合理提取特征。

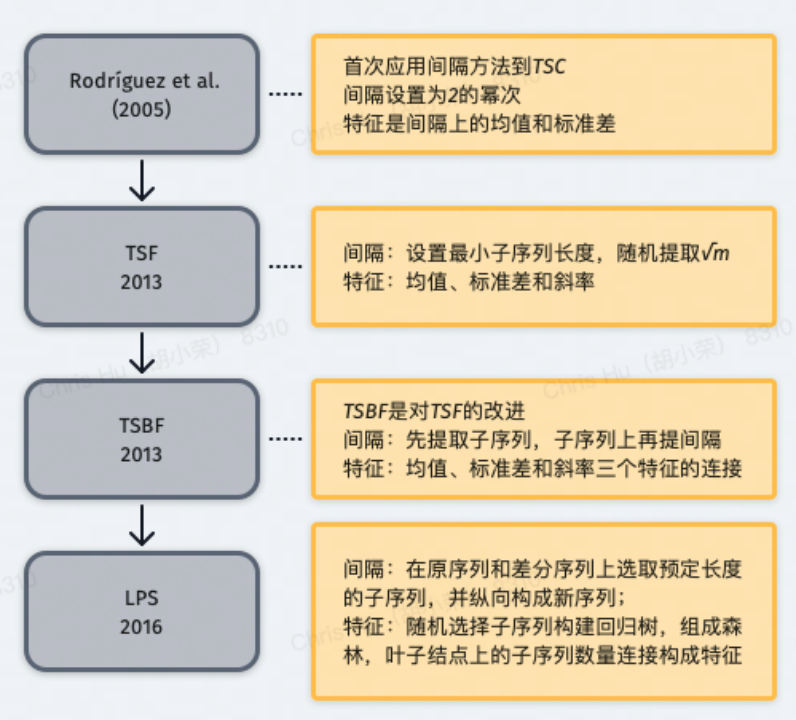
關鍵問題解決方法如下（TSF-Time Series Forest）：

采用隨機森林的方法解決序列區間數量大的問題，采用統計值作為特征；

長度為 m 的序列，提取 sqrt (m) 個區間，每個區間上提取均值、標準差和斜率三個特征，共 3*sqrt (m) 個特征用于訓練；

分類結果由集成的所有樹的多數投票決定；

基于 shapelets 的分類算法

shapelet 分類算法通過在序列中查找最具辨別性的子序列用于分類，其中 shapelet 指一個與位置無關的最佳匹配子序列。該類算法適用于可以通過序列中的一種模式定義一個類，但是與模式的位置無關的分類問題。主要有以下兩個研究方向：

shapelet 尋找：枚舉所有可能的 shapelet，挑選最好的；

shapelet 用法：將 shapelet 用于決策樹的結點分裂準則。

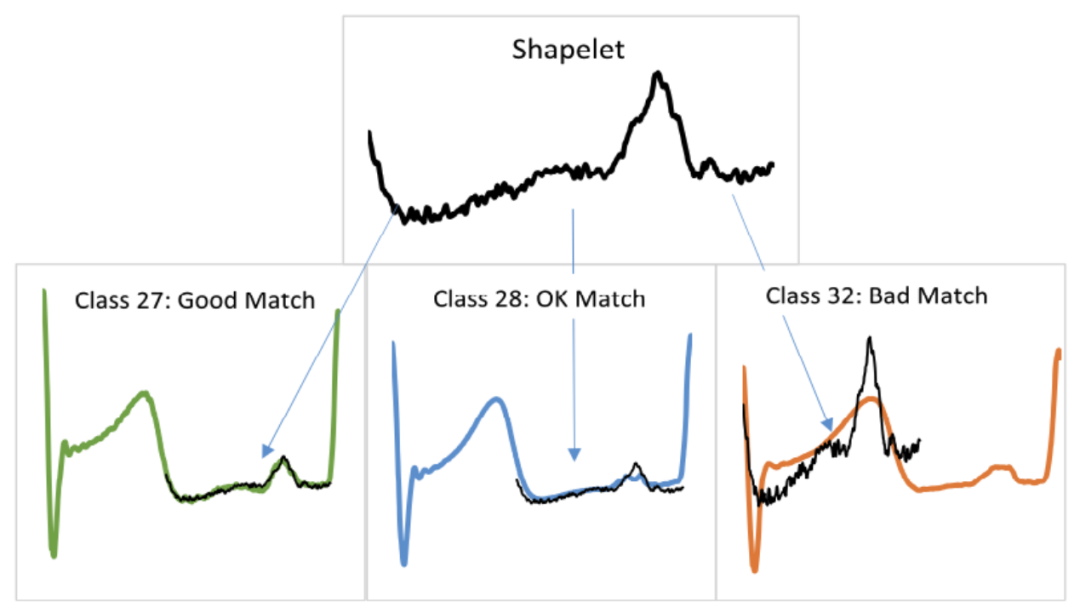
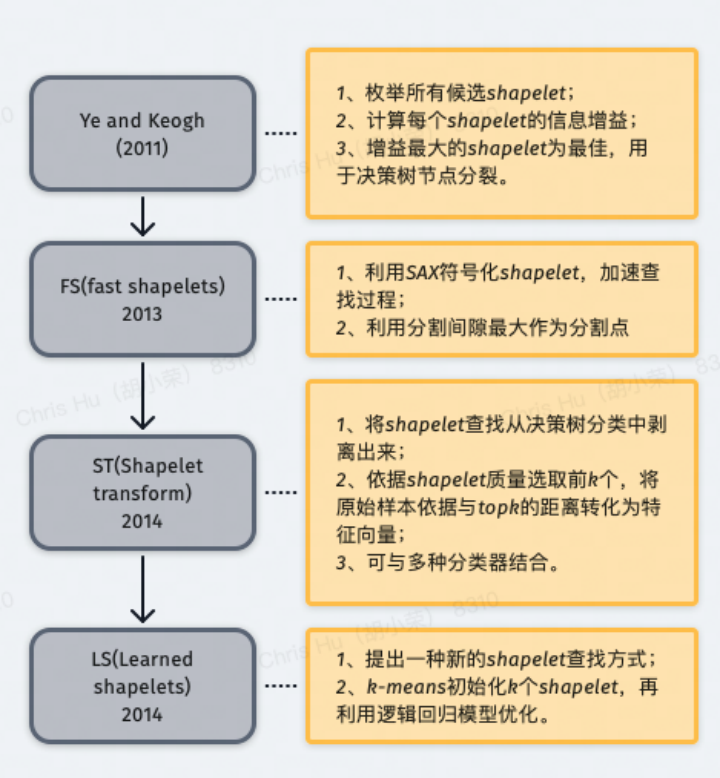
shapelet 分類算法通過在序列中查找最具辨別性的子序列用于分類，其中 shapelet 指一個與位置無關。

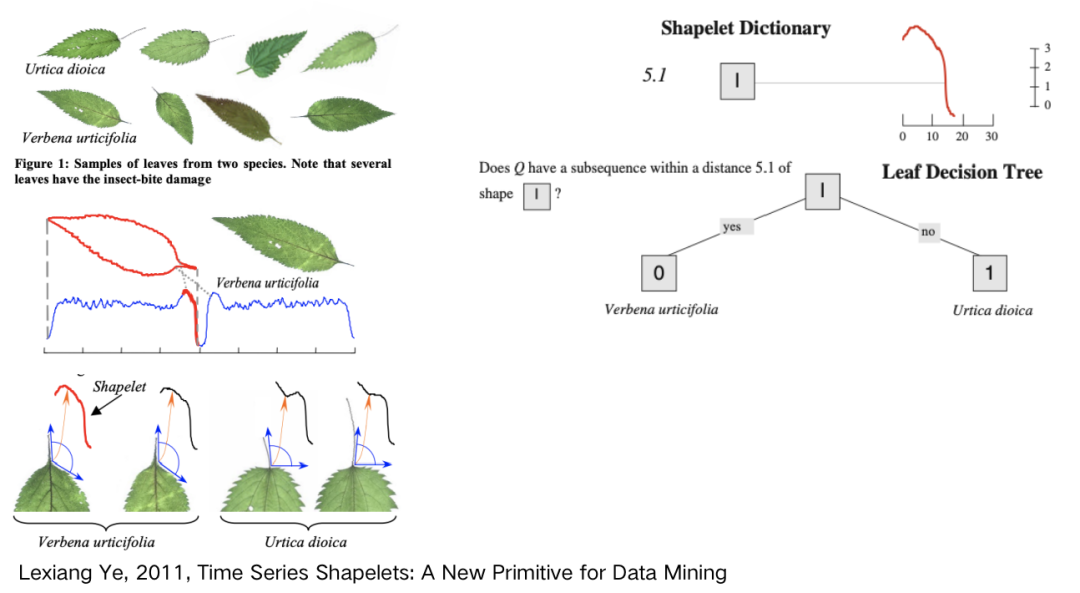
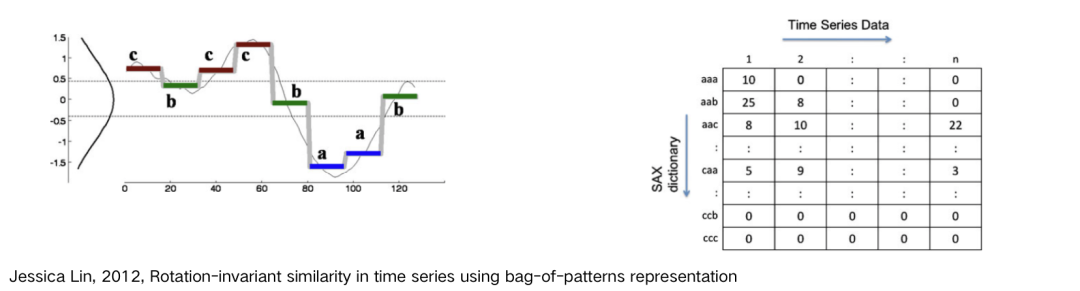
基于詞典的分類算法

由于 shapelet 分類算法需要花費大量時間搜索子序列，因此更適用于短序列。對于長序列，更適用于在高級結構上衡量相似度。此外，shapelet 只使用一個最佳匹配進行分類，無法解決區別在模式重復數量上的分類問題。因此，對于長序列中一種模式反復出現的時間序列，更適用于一種叫做 dict 詞典類的分類算法。 基于詞典的分類算法原理是以序列中的子序列的重復頻率作為特征進行分類。首先對序列進行降維和符號化表示，形成單詞序列，然后根據單詞序列中的單詞分布情況進行分類。特點是通過給每個序列傳入一個長度為 w 的滑動窗構建單詞，每一個窗產生 l 個近似值，將每個值離散化，對應到一個字母表中的符號。 BOP - Bag of Patterns 采用了類似 “bag of words” 的思路，將時間序列表示成一系列模式的向量。存在問題如下：

需要構建 “模式詞匯表 -> SAX

時間序列沒有明顯分隔符進行分割。- 滑動窗口

操作步驟如下：

BOP 算法采用滑動窗口在原始序列上取子序列；

再利用 SAX 方法將子序列轉化為單詞，并記錄每個單詞數量，所有的單詞匯總為詞匯表；

最后構建 “單詞 - 句子” 向量矩陣，行是詞匯表，列是每個時間序列，點的值是詞匯在序列中的出現頻率。

_x0008_SAX (Symbolic Aggregate Approximation) 對序列進行正則化，在橫軸方向，將時間序列等長劃分為 w 段，計算每一段的均值，并將 w 個系數聚集在一起，這個過程稱為分段聚集近似（Piecewise Aggregate Approximation，PAA）。 研究表明正則化的時間序列的子序列服從高斯分布，在縱軸方向，將均值從高斯分布等概率劃分為三塊區域，位于每個區域的系數分別用 a,b,c 表示，此時序列已轉化為字符串。

審核編輯：郭婷