本文介紹數字預失真(DPD)的數學基礎,以及如何在收發器的微處理器和硬件中實現它。它解決了現代通信系統需要DPD的原因,并探討了數學模型如何捕獲真實世界的信號失真。
介紹
DPD 是許多 RF(射頻)工程師、信號處理愛好者和嵌入式軟件開發人員熟悉的首字母縮略詞。DPD在我們的蜂窩通信系統中無處不在,使功率放大器(PA)能夠有效地為天線提供最大功率。隨著5G推動基站的天線數量增加,我們的頻譜變得越來越擁擠,DPD已成為一項關鍵技術,允許開發高效,具有成本效益和規范兼容的蜂窩系統。
我們中的許多人根據自己的觀點對DPD有獨特的理解,無論是從純數學角度還是從微處理器上更受約束的實現。也許您是一名評估RF基站產品中DPD性能的工程師,或者對數學建模技術如何在現實世界系統中實現感到好奇的算法開發人員。本文旨在拓寬您的知識面,使您能夠從各個角度充分掌握該主題。
什么是DPD,為什么使用它?
當RF信號從基站無線電輸出時(見圖1),在通過天線傳輸之前需要放大。射頻PA用于執行此操作。在理想情況下,PA接受輸入信號并輸出與其輸入成比例的更高功率信號。它還以最節能的方式做到這一點,以便將提供給放大器的大部分直流電源轉換為信號輸出功率。
圖1.帶和不帶DPD的簡化無線電結構框圖。
然而,這不是一個理想的世界。PA由晶體管制成,晶體管是有源器件,本質上是非線性的。現在,如果我們在PA的“線性”區域使用PA(此處為線性是一個相對術語;因此為引號),如圖2所示,則輸出功率與輸入功率相對成正比。這種方法的缺點是PA通常在非常低效的狀態下使用,提供的大部分功率都以熱量的形式損失。我們經常希望在PA開始壓縮時使用它們。這意味著,如果輸入信號增加設定量(例如3 dB),PA輸出不會增加相同的量(可能僅增加1 dB)。顯然,此時信號被放大器嚴重失真。
圖2.PA輸入功率與輸出功率的關系圖(顯示采樣輸入/輸出信號的投影)。
這種失真發生在頻域中的已知位置,具體取決于輸入信號。圖3顯示了這些位置以及基頻與這些失真產物之間的關系。在RF系統中,我們唯一需要補償的失真是那些接近基波信號的失真,即奇階互調產物。系統中的濾波負責帶外產物(諧波甚至階次交調產物)。圖4顯示了RF PA在其壓縮點附近運行的輸出。互調產物(尤其是三階)清晰可見。它們看起來像所需信號周圍的“裙子”。
圖3.2 音輸入的互調和諧波失真位置。
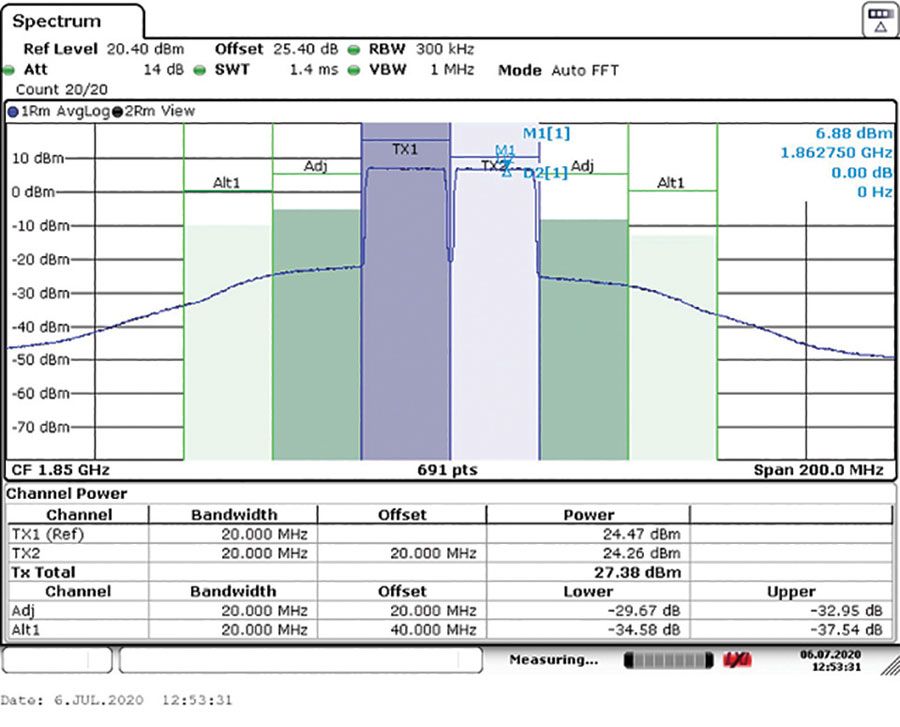
圖4.2× 20 MHz載波通過SKY66391-12射頻PA。中心頻率 = 1850 MHz。
DPD旨在通過觀察PA輸出來表征這種失真,并在知道所需的輸出信號后改變輸入信號,使PA輸出更接近理想值。這只有在相當具體的情況下才能有效地完成。我們需要配置放大器和輸入信號,使放大器有所壓縮,但不會完全飽和。
PA 失真建模背后的數學原理
看到希臘字母和其他數學符號是否往往會帶來對過去大學考試的可怕閃回?你并不孤單!當人們得到的第一個參考文獻是一篇數學繁重的學術論文時,人們可能會不必要地被基礎知識所推遲。論文“RF功率放大器數字預失真的廣義記憶多項式模型”1是一項開創性的工作,介紹了廣泛采用的廣義記憶多項式 (GMP) 方法 DPD。如果您只是涉足信號處理方面的事情,那么介紹該主題可能會有點沉重。因此,作為開始,讓我們嘗試分解GMP方法,并更直觀地理解數學正在做什么。
Volterra系列是DPD的數學支柱。它用于用內存對非線性系統進行建模。內存只是意味著系統的當前輸出可以依賴于當前和過去的輸入。Volterra系列非常通用(因此功能強大),用于電氣工程以外的許多領域。對于PA DPD,Volterra系列可以精簡,使其在實時數字系統中更具可實施性和穩定性。GMP就是這樣一種瘦身的方法。
圖 5 描述了如何使用 GMP 對 PA 的輸入 x 與其輸出 y 之間的關系進行建模。您將看到等式的三個獨立求和塊彼此非常相似。讓我們專注于下面以紅色突出顯示的第一個。|x(。..)|k項稱為輸入信號的包絡,其中 k 是多項式階。l 將內存整合到系統中。如果 L一個= {0,1,2},則模型允許輸出 y藥品監督管理總局(n) 取決于當前輸入 x(n) 和過去的輸入 x(n – 1) 和 x(n – 2)。圖 6 檢查了多項式階數 k 對樣本向量的影響。矢量x是單個20 MHz載波,繪制在復基帶上。通過去除內存組件簡化了GMP建模公式。x|x的圖|k與圖4中可見的真實失真有明顯的相似之處。
每個多項式階數 (k) 和內存滯后 (l) 都有一個相關的復權重 (a吉隆坡)。當選擇了模型的復雜性(將包括k和l的值)時,有必要根據對已知輸入信號的PA輸出的實際觀察來求解這些權重。圖 7 將簡化的方程轉換為矩陣形式。使用的數學符號允許對模型進行簡潔的表示。但是,對于DPD在數字數據緩沖區上的實際實現,以矩陣表示法查看事物是最簡單且更具代表性的。
讓我們簡要看一下圖 6 中公式的第二行和第三行,為簡單起見,忽略了它們。請注意,如果 m 設置為零,則這些行將與第一行相同。這些線路允許在包絡項和復基帶信號之間添加延遲(正和負)。這些稱為滯后和前導交叉項,可以顯著提高DPD的建模精度。它們為我們嘗試模擬放大器的行為提供了額外的自由度。請注意,Mb, Mc, Kb和 Kc不包含零;否則,我們將重復第一行中的術語。
圖5.用于模擬PA失真的GMP。1
圖6.階數 (k) 對信號 x 頻域中信號的影響圖。
圖7.將簡化的公式轉換為數據緩沖區上的矩陣運算(更接近數字實現方式)。
那么我們如何確定模型的順序、記憶項的數量以及我們應該添加哪些交叉項呢?這就是一定數量的“黑魔法”進入事物的地方。在某種程度上,我們可以從我們對失真物理學的知識中獲得指導。放大器的類型及其制造材料以及通過它播放的信號帶寬都會影響建模術語,并允許在該領域有經驗的工程師對應該使用哪種模型進行限制。但是,在此之上還涉及一定程度的試驗和錯誤。
從數學角度要解決的問題的最后一個方面,既然有建模結構可用,是如何求解加權系數。在實際場景中,傾向于求解上述模型的逆函數。事實證明,這些模型系數有一個很好的互惠性,因為相同的權重可用于對捕獲的PA輸出矢量進行后失真,以消除非線性,并對通過PA發送的傳輸信號進行預失真,使PA輸出看起來盡可能線性。圖8顯示了如何進行權重系數估計和預失真的框圖。
圖8.描述建模和預失真間接實現的框圖。
對于逆模型,將圖 7 中給出的矩陣方程交換,得到 X? = Yw。此處矩陣 Y 的形成方式與 X 在另一種情況下的形成方式相同,如圖 9 所示。對于此示例,已包含內存項,并且已減少包含多項式階數。為了求解w,我們需要得到Y的逆,Y不是正方形的(它是一個高而細的矩陣),所以這是使用矩陣“偽逆”來實現的(見公式1)。這在最小二乘意義上求解了 w,也就是說,它最小化了 X? 和 Yw 之間差的平方,這就是我們想要的!
這可以進一步完善,以考慮到它正在具有不同信號的實時環境中應用。在這里,系數通過從其先前的值更新來約束。μ 是一個介于 0 和 1 之間的常量值,用于控制每次迭代權重可以更改的程度。如果 μ = 1 且 w0= 0,則此方程立即恢復為基本最小二乘解。如果μ設置為小于 1 的值,則系數需要多次迭代才能收斂。
請注意,此處描述的建模和估計技術并不是執行DPD的唯一方法。也可以使用基于動態偏差減少 (DDR) 的建模等技術來代替或補充它。描述的用于求解系數的估計技術也可以通過多種方式完成。鑒于這是一篇短文而不是一本書,讓我們把它留在那里。
我們如何在微處理器中實現這一點?
好的,數學已經完全涵蓋了。下一個問題是它如何應用于現實世界的通信系統?它在數字基帶中實現,通常在微處理器或FPGA中實現。ADI公司的RadioVerse收發器產品(如ADRV902x系列)內置微處理器內核,其結構經過專門設計,可輕松實現DPD。?
圖9.矩陣形式的逆接近方程。此處包含了一些內存。
圖 10.具有一個記憶抽頭和一個三階交叉項元件的三階情況的預失真計算。
嵌入式軟件中的DPD實現有兩個不同的方面。第一個是DPD執行器,它是實時執行實時傳輸數據的預失真的地方,第二個是DPD自適應引擎,它是根據PA輸出的觀察結果更新DPD系數的地方。
如何在微處理器或類似處理器中實時實現DPD和許多其他信號處理概念的關鍵是通過使用查找表(LUT)。LUT 允許用更簡單的數組索引操作代替昂貴的運行時計算。讓我們考慮DPD執行器如何將預失真應用于傳輸的數據樣本。符號如圖 8 所示,其中 u(n) 是要傳輸的數據的原始樣本,x(n) 是預失真版本。圖 10 顯示了在給定場景中獲得一個預失真樣本所需的計算。這是一個相對有限的示例,最高多項式階數為三階,只有一個記憶抽頭和一個交叉項。即使對于這種情況,顯然也需要大量的乘法、冪和加法計算來獲得這一個數據樣本。
這就是LUT可以減輕實時計算負擔的地方。圖10可以改寫為圖11,其中將在LUT中輸入的數據變得更加明顯。每個LUT都包含|u(n)|的大量可能值的公式中突出顯示的元素的結果。分辨率取決于可在可用硬件中實現的LUT的大小。電流輸入樣本的幅度根據LUT的分辨率進行量化,并用作索引,以訪問給定輸入的正確LUT元件。
圖 11.重新組合方程元素以顯示LUT的結構。
圖12顯示了如何將LUT集成到我們示例案例的完整預分配執行器實現中。請注意,這只是眾多可能實現中的一個。在保持相同輸出的同時可以進行更改的一個例子是延遲元素 z–1,可以移動到 LUT2 的右側。
圖 12.使用 LUT 可能實現 DPD 的框圖。
自適應引擎的任務是求解用于計算執行器中LUT值的系數。這涉及求解方程1和2中描述的w向量。偽逆矩陣運算,(YHY)-1YH,計算量很大。等式 1 可以改寫為
如果 CYY= YHY 和 CYx= YHx,則等式 3 變為
CYY是一個方陣,可以分解為上三角矩陣L及其共軛轉置(CYY=LHL)使用喬列斯基分解。這允許我們通過引入一個虛擬變量 z 并求解它來求解 w,如下所示:
然后將這個虛擬變量替換回去以求解
因為L和LH分別為上三角矩陣和下三角矩陣,公式5和公式6易于求解,計算費用最低,得到w。每次運行自適應引擎并找到 w 的新值時,都需要更新執行器 LUT 以反映它們。自適應引擎可以根據對PA輸出的觀察或操作員對要傳輸的信號變化的了解,以設定的定期間隔或更不規則的間隔執行。
在嵌入式系統中實現DPD需要大量的制衡,以確保系統的穩定性。傳輸的數據緩沖區和捕獲緩沖區數據在時間上對齊至關重要,以確保它們之間建立的數學關系是正確的,并且在隨著時間的推移應用時成立。如果失去這種對齊,則自適應引擎返回的系數將無法正確預扭曲系統,并可能導致系統不穩定。還應檢查預失真的執行器輸出,以確保信號不會使DAC飽和。
結論
希望本文通過檢查底層數學及其在硬件中的實現,解開了DPD的一些謎團。這只是這個迷人主題的冰山一角,可能會促使讀者進一步研究信號處理技術在通信系統中的應用。Pratt和Kearney的研究是關于DPD應用于有線通信系統中超寬帶寬用例的良好來源。2ADI公司的RadioVerse收發器產品具有獨特的優勢,可集成DPD等算法,為客戶提供高度集成的RF硬件和可配置的軟件工具。
審核編輯:郭婷
-
功率放大器
+關注
關注
102文章
3518瀏覽量
131658 -
微處理器
+關注
關注
11文章
2247瀏覽量
82320 -
RF
+關注
關注
65文章
3042瀏覽量
166827 -
無線電
+關注
關注
59文章
2131瀏覽量
116316
發布評論請先 登錄
相關推薦




 數學模型如何捕獲真實世界的信號失真
數學模型如何捕獲真實世界的信號失真

















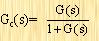










評論