1邏輯函數的化簡方法
本文通過具體題目來總結邏輯函數的化簡方法:
總的來說包括兩大部分:公式化簡法和卡諾圖化簡法:
一、公式化簡法
①并項法:AB + AB'= A
例:
Y1=A(B'CD)'+AB'CD=A[(B'CD)'+B'CD]=A; Y2=AB'+ACD+A'B'+A'CD=B'(A+A')+CD(A+A')=B' + CD; Y3=A'BC' + AC' + B'C' = A'BC' + (A + B')C' = A'BC' + (A'B)'C' = C'; Y4=B(C'D+CD')+B(C'D'+CD)=B(C^D)+B(C^D)'=B;
這種方法本質上是類似于合并同類項,將剩余部分構造成A + A’的形式;其中Y3和Y4需要稍微注意一下。
[注]^代表的是異或,()'代表的是取非。
②吸收法:A + AB = A
例:
Y1=((A'B')'+C)ABD+AD=((A'B')'+C)BAD+AD=AD; Y2=AB+ABC'+ABD+AB(C'+D')=AB+AB(C'+D+C'+D')=AB; Y3=A+(A'(BC)')'(A'+(B'C'+D)')+BC=A+(A+BC)(A'+(B'C'+D)')+BC=A + BC;
其中,Y3中,化簡出(A + BC)后,將式子乘開,則后面每一項中要么含有A,要么含有BC,所以,可以直接使用吸收法得出最后結果。
吸收法的本質類似于數學中的大小集合問題,畫個卡諾圖來解釋一下:
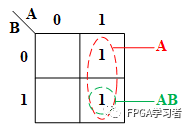
可以看到,A的范圍比AB要大,所以他們屬于一個包含關系,在A為真的情況下,則AB一定為真,故A + AB = A;
③消項法:AB + A'C + BC = AB + A'C ,AB + A'C + BCD = AB + A'C
例:
Y1=AC+AB'+(B+C)'=AC+AB'+B'C' = AC + B'C'; Y2=AB'CD'+(AB')'E+ A'CD'E = AB'CD' + (AB')'E; Y3=A'B'C+ABC+ A'BD' + AB'D' + A'BCD' + BCD'E' =C(A^B)'+D'(A^B)+CD'(B(A' + E')) = C(A^B)' + D'(A^B);
注意出題的時候,不一定按照常規的公式來出,有可能換著字母出題,讓人覺得不適應。第一個公式和第二個公式之間,很明顯暗含了一個吸收法的公式,因為BC所表示的范圍要比BCD大,所以第一個公式成立的話,那么第二個公式一定成立。
④消因子法:A + A'B = A + B;
例:
Y1=B'+ABC=B'+AC; Y2=AB'+ B + A'B = B + A + A'B = A + B; Y3=AC+A'D+C'D=AC+(A'+C')D=AC+(AC)'D=AC+D;
⑤配項法:
1.根據基本公式:A + A = A;所以,邏輯函數中重復寫入某一項,有時能夠獲得更加簡單的化簡結果。
Y=A'BC'+A'BC+ABC;重復寫入A'BC 所以:Y =(A'BC'+A'BC)+(A'BC+ABC)=A'B+BC;
2.根據基本公式A + A'=1;所以,可以在函數式中的某一項乘以(A+A'),然后拆分成兩項分別與其他項合并,有時可以得到更加簡單的結果。
例:
Y = AB' + A'B + BC' + B'C = AB' + A'BC + A'BC' + BC' + AB'C + A'B'C =(AB'+AB'C)+(BC'+A'BC')+(A'BC+A'B'C) = AB' + BC' + A'C
二、卡諾圖化簡法
卡諾圖化簡比較直觀簡單,一般可以用于公式法化簡之后的驗證!
三、考研真題解析
(2017山東大學考研906)用公式化簡:F=AD+BCD'+(A'+B')C
【解析】
常規想法:
F = AD + BCD' + A'C + B'C =AD+C(B' +BD')+A'c =AD+C(B'+D')+A'C =AD+C(A'+B'+D') ……
好像做不動了,怎么去解決這個問題呢?
用卡諾圖!
雖然題目中,明確規定使用公式法化簡,但是此處想不到用什么公式怎么辦,那就從卡諾圖入手,看看是否有突破口,然后反推公式法化簡。
卡諾圖如下:
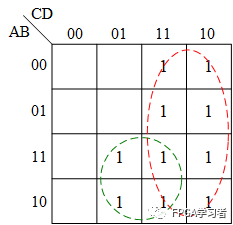
可以得出最后的結果是:AD + C;
怎么由這個結果往回推呢?
首先:前面得到F = AD + BCD' + A'C + B'C
F=AD+BCD'+A'C+B'C //式子中已經有AD,暫時不用處理
在卡諾圖中,除去AD的部分,再把其余表達式在卡諾圖中標出來,可以看到,剩余的部分無論怎樣都無法構成C,少了一項ABCD:
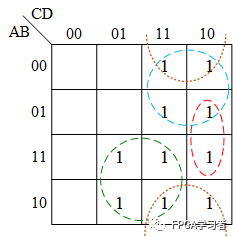
所以,需要從AD(綠圈)中分出一部分來,即下圖中粗長方形圈的部分:
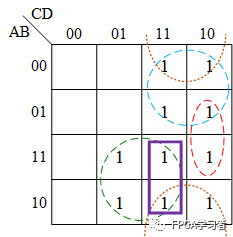
這便相當于在原有的表達式中添加了一項:ACD
即:
F = AD + BCD' + A'C + B'C = AD + ACD + BCD' + A'C + B'C =AD+C(A'+ AD)+C(B'+BD') =AD+C(A' + D) + C(B' + D') =AD+A'C+CD+B'C + CD' =AD+C(D'+D)+A'C + B'C = AD + C + A'C + B'C = AD + C
【總結】
上題旨在分析添加某一項的思想。
添加某一項來幫助化簡,本身就是一個比較難想出來的過程;通過卡諾圖畫圖分析的形式,可以幫助我們理解為什么要添加某一項。并且,這樣做也可以在遇到困難的題目,實在解決不了時,當成一個急救的辦法。
審核編輯:湯梓紅
-
邏輯函數
+關注
關注
0文章
23瀏覽量
9475 -
函數
+關注
關注
3文章
4234瀏覽量
61961 -
數字電子
+關注
關注
6文章
99瀏覽量
21127
原文標題:數字電子技術基礎----邏輯函數的化簡方法
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
數字電子技術基礎教學大綱
數字電子技術教程之邏輯代數基礎的詳細資料概述
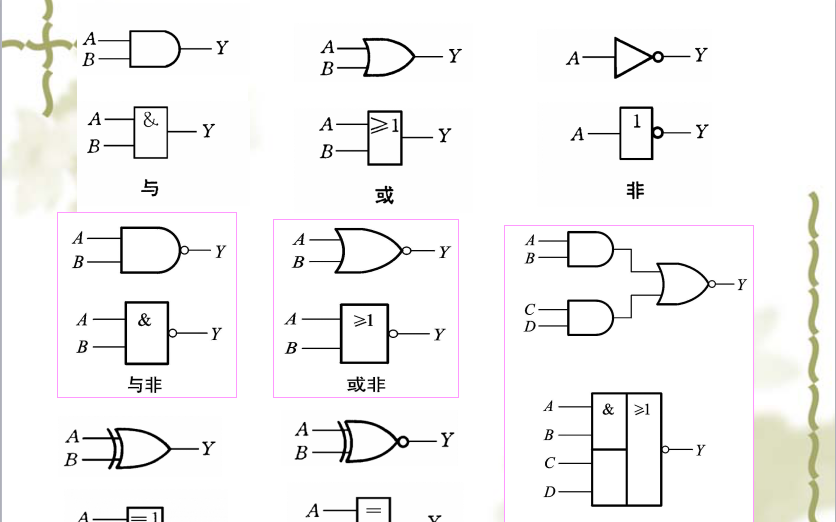




 數字電子技術基礎----邏輯函數的化簡方法
數字電子技術基礎----邏輯函數的化簡方法










評論