一. 前言
你好,歡迎你打開這篇文章,這是我的系列立體匹配算法介紹文章中承上啟下的一篇,請看看我們現在走到了哪一步:
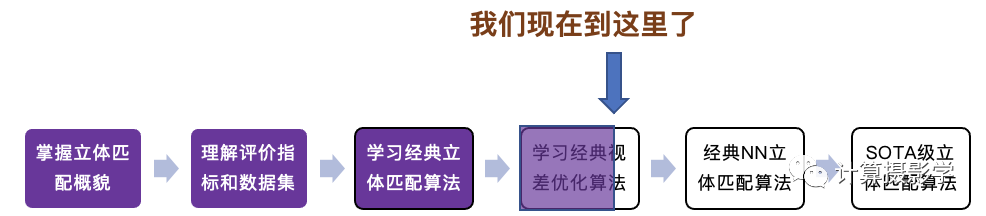
當前進度 今天,我將通過這一篇文章,填滿上圖箭頭指向的格子! 下面我展示了一對雙目相機拍攝的原始圖像,已經過了立體校正:

一對做過立體校正后的雙目圖像 而下面左圖是OpenCV的SGBM算法得到的視差圖,右邊則是通過我今天要介紹的算法處理后的視差圖。看了它們后,我想你應該對什么叫做”化腐朽為神奇“有了深刻印象了吧。

左:SGBM算法結果 右:今日介紹的算法結果 那么如此神奇的效果,是如何做到的呢? 在復雜的問題進行空間轉換,變換為小規模的易解問題的思想:
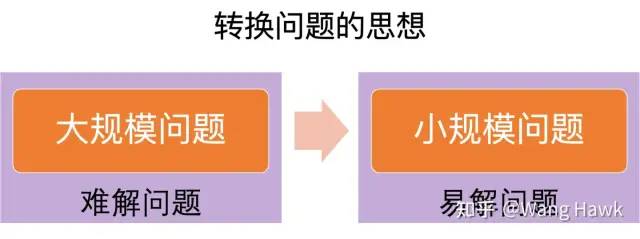
化簡問題的思路 今天我介紹的這篇文章,也是基于這種思想的——事實上這就是同一個作者Jon Barron,基于相同思想的進一步研究,

Jon Barron文章介紹 這個算法我在后文中會簡稱為FBS,它是我在立體匹配的研究和工程應用中最喜歡的算法之一。這個算法相比我之前介紹的Fast Bilateral-Space Stereo有什么不同呢? 上一篇文章所講的Fast Bilateral-Space Stereo,解決的是立體匹配問題——它將立體匹配當成下面的全局匹配代價最小化問題進行解決。

Fast Bilateral-Space Stereo算法思想總結 這個算法的優點我們已經講過了,在此不再贅述。然而它也有明顯的缺點。 首先是其匹配代價函數過于簡單,上面公式中第二項是就是匹配代價項,也即是數據項。為了盡可能簡單快速求解,作者采用了下面這樣非常簡單的形式:
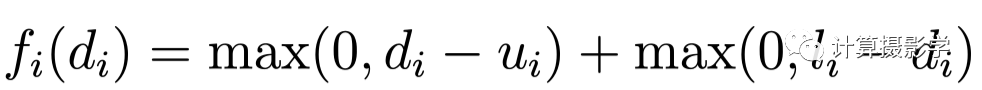
簡化的立體匹配代價函數 圖示如下:
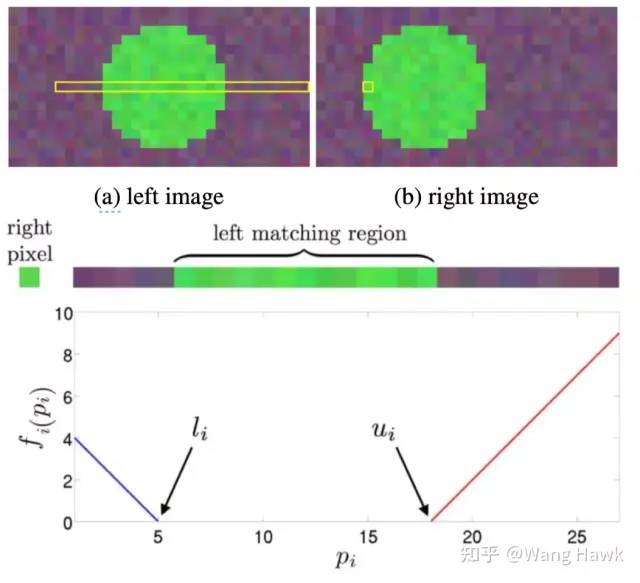
圖示這種簡化問題的思路 然而,正是因為其形式非常簡單,因此效果也不夠好,很容易出現大大小小的錯誤。 Fast Bilateral-Space Stereo算法的另外一個問題是,作者把上述代價映射到了雙邊空間,用一種叫做L-BFGS的方法進行求解,這是Broyden,Fletcher,Goldfarb,Shanno這幾位數學家發明的優化算法,他們名字的首字母組合就是BFGS。這是一種迭代式的求解方法,它的求解速度是比較慢的。
同時,Fast Bilateral-Space Stereo的求解方法也無法應用到深度學習過程中,因為其代價函數也無法求導進行反向傳播。這一點我之后再談。 今天要講的FBS,則采用了特別不一樣的思想,如下圖所示。Fast Bilateral-Space Stereo的一大缺點就是采用了較低質量的匹配函數,所以Fast Bilateral Solver(即所謂FBS)干脆不自己做匹配,而是允許其他算法算出一個初始的還不夠好的視差圖,然后再通過最優化一個全局代價函數來優化這個初始的視差圖,最終得到一個更好的結果:
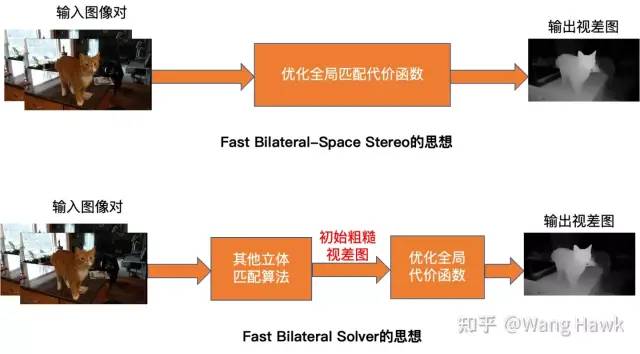
FBS思想 在作者論文中開篇就用下面這幅圖來說明了這個思想:

利用FBS優化視差圖 我一開始給大家呈現的關于貓貓的視差圖(下面右圖),就是用FBS處理了SGBM算法的結果(左圖)后得到的,這也是我最喜歡的FBS的用法:

左:SGBM算法結果 右:FBS優化左圖的結果 FBS的優秀之處在于它不僅僅可以用于優化初始的視差圖,還能做得更多,比如視差圖或深度圖圖的超分辨率重建。這里有一個低質量的輸入視差圖y,以及一個參考圖像R,通過FBS可以得到高質量的輸出圖像x,其中x相對于參考圖像R滿足雙邊平滑的特性,且其邊緣貼合參考圖像的邊緣,同時x還與輸入圖像y盡可能相似。
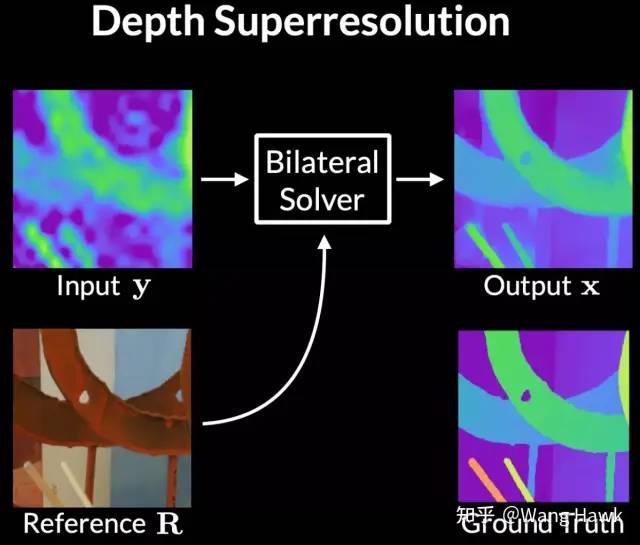
在圖像超分鐘應用FBS 另外一個有趣的應用是用戶引導的灰度圖像上色。這里也有低質量的輸入圖像y,即用戶指定的最終色彩圖像的骨架,原始的灰度圖像則作為參考圖像。再指定一個置信度圖c,我們一樣通過FBS求解輸出彩色圖像x,并且要求x自身相對參考圖像來說是雙邊平滑的,同時還在高置信度的區域和用戶輸入y盡可能一致。
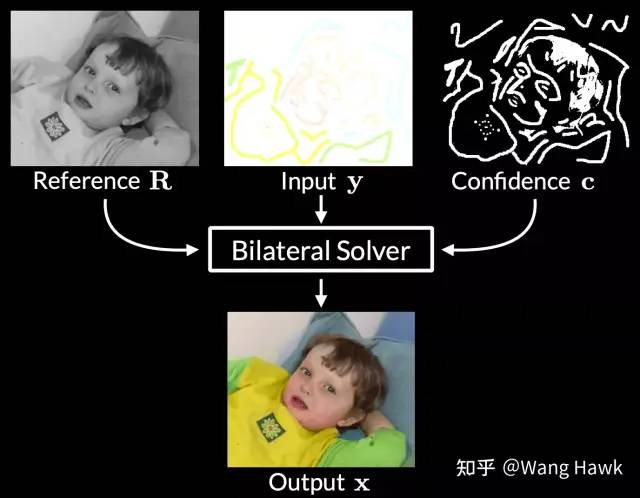
在圖像上色中應用FBS 看出來了吧?FBS算法可以用于優化任意的輸入圖像,只要給出了一個參考圖像和一個目標圖像,它就會努力的讓輸出圖像既能夠按照參考圖像來雙邊平滑,又能夠非常接近目標圖像,所以這是一種非常通用的算法。那么在下一節中,我們從原理上理解一下FBS算法。
二. FBS算法的應用目標和原理
2.1 FBS算法要解決的問題
用數學公式更加嚴謹的說明一下FBS吧。我們的目標是求解一個未知的圖像x,它本身相對于參考圖像R是雙邊平滑的(下式第1項),但在高置信度的區域又是和輸入的目標圖像t又是非常接近的。

FBS試圖優化的全局代價函數 剛才給過的這張圖,清晰的展示了上面公式的4張圖。左上圖為目標圖像t,是由一個立體匹配算法得到的初始視差圖。而右上圖是輸出圖x,是經過FBS優化得到的結果。左下圖是置信度圖c,右下圖則是輸入的參考圖像R,上面公式中的W就是由輸入參考圖像R計算而來的。
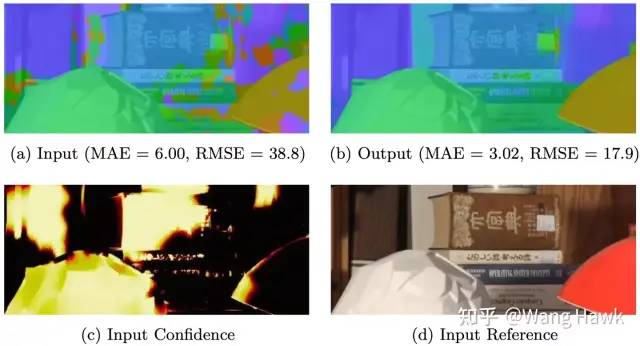
FBS應用到視差后處理優化的示例
2.2 將問題轉換到雙邊空間
求解上述的最小化的問題非常復雜,于是我們沿用上一次講到的思想,將問題轉換到雙邊空間中去求解。不過,FBS和Fast Bilateral Stereo算法在雙邊空間中的表達式有關鍵的區別:

在雙邊空間中比較FBS及Fast Bilateral-Space算法 可以看到,FBS在雙邊空間中的求解非常簡單,直接求解一個線性等式Ay=b即可,這是因為FBS不再需要承擔做立體匹配的職責,它只需要保證優化后的視差圖滿足雙邊平滑以及與初始視差圖盡可能相似即可。 當在雙邊空間中求得了y,接下來就再用下面的公式把結果轉換為像素空間,就可以得到像素空間中的優化后的視差圖了:

看起來是不是很簡單?所以上面公式中最關鍵的就是要找出公式(6)中A和b及c的表達式,作者論文中已經給出:
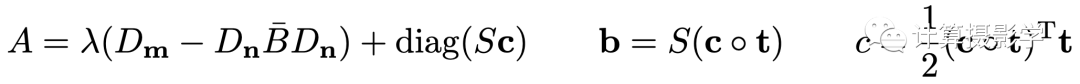
下面我們再解釋一下上面幾個公式中的各個變量:
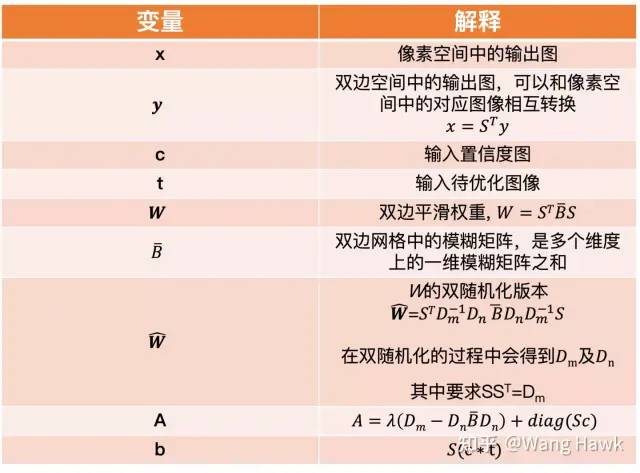
公式變量解釋 當構造了上面提到的Ay = b這樣的等式之后,作者采用了一種叫做preconditioned conjugate gradient (PCG)的算法(帶先驗條件的共軛梯度算法)來優化它,并且在這個過程中還采用了級聯金字塔的思想。這個過程略去不表,咱們只需要知道,采用了這種方式之后,整個問題的構建和優化速度都比之前介紹的Fast Bilateral Stereo大大加快了:
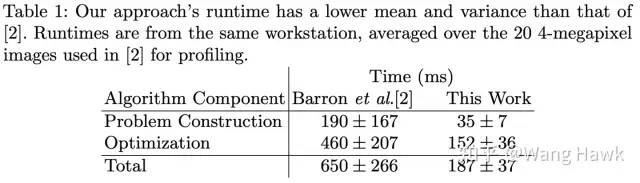
FBS的優化速度大大提升 在應用到對初始視差圖進行優化的過程中,作者考慮到FBS的輸出結果對于給定的置信度圖和初始視差圖比較敏感,還采用了一種迭代式的求解形式, 這個過程中的公式推導比較復雜,限于篇幅所限,這里我就略過了推導的過程。但作者給出了粗糙版的Python實現,在OpenCV里面也有相應的實現。我會在我的知識星球中,針對這兩份代碼做進一步的解釋說明。
三. FBS的應用效果
讓我先展示一些作者論文中的FBS的效果吧。首先我們看看一個當時最優秀的立體匹配算法MC-CNN的結果,這是第一代基于深度學習的立體匹配算法。下面是Middle Burry立體匹配數據集中的一幅圖,從下圖中看來,它在很多邊緣細節上還是出現了錯誤和瑕疵:

MC-CNN算法結果 現在來看看經過FBS處理優化后的結果,我們看到從視覺上視差圖結果明顯好了一個檔次,MAE和RMSE也有所降低,雖然bad 1%這個指標略有上漲。

用FBS優化MC-CNN算法結果大大減少了錯誤 下面是另外一張,很明顯MC-CNN出現了很多瑕疵,尤其是近距離處出現很多匹配錯誤

下面是經過FBS優化后的結果,很明顯視覺效果好了不少,MAE和RMSE也少了很多!

用FBS優化MC-CNN算法結果大大減少了錯誤
四. 可導性與深度學習
作者還花了不少篇幅來講解將FBS作為一個“層”應用到深度學習的過程中,這里我也提一提吧。以語義分割為例,我們設想中將FBS作為網絡的一個層加入到網絡的輸出部分,如下圖所示,其目的是優化網絡輸出的分割掩模:

現在我們來看看現在比較常見的卷積神經網絡優化損失函數的過程,下面是這個過程的圖示:
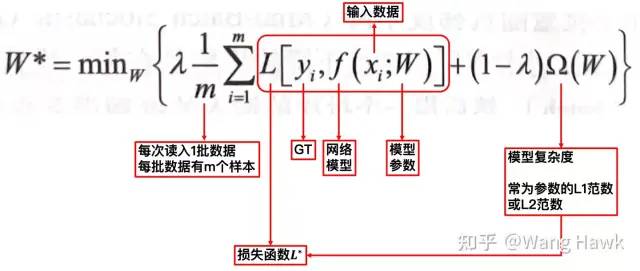
深度學習用于優化復雜的目標函數 直接優化上述函數是很困難的,所以實際中一般會采用小批量隨機梯度下降法來求解
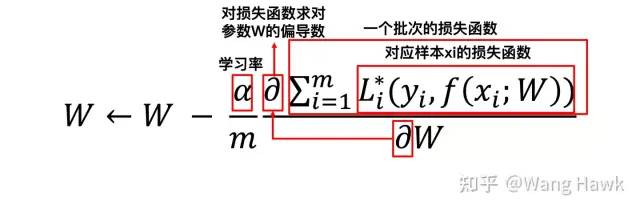
梯度下降法要求損失函數可導 所以這里很關鍵的就是損失函數要能夠對各個待優化參數求偏導數,要在反向傳播的過程中可導。如果我們把FBS作為網絡的一個層,應用到網絡構建的過程中,也會要求它可導。
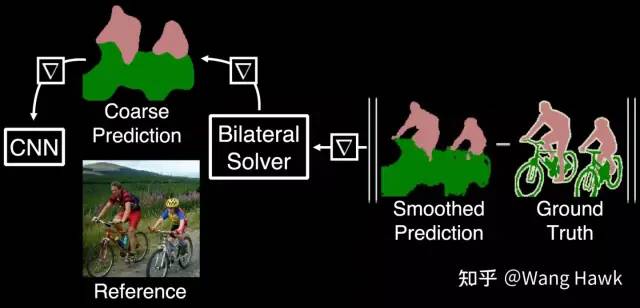
在反向傳播中要求FBS可導 在FBS之前有很多全局能量優化的算法,都很難做到這一點。幸運的是,作者證明了FBS是可以用于反向傳播的,我們把FBS看做下面這樣的函數
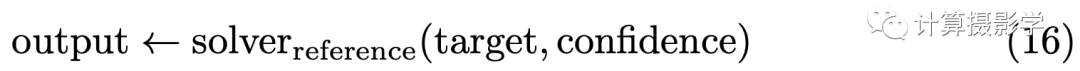
那么反向傳播需要求解它對于輸入的兩幅圖像的偏導數:
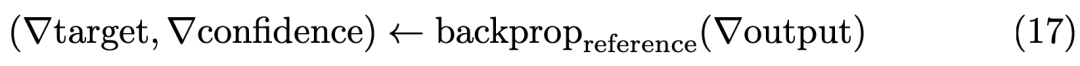
作者在論文中給出了兩個偏導數的公式:
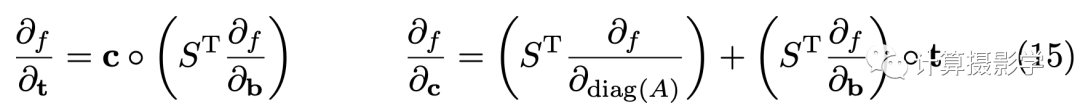
作者給了一個例子,來說明引入了FBS到網絡中的好處,首先是用Deeplab進行分割后的粗糙結果:
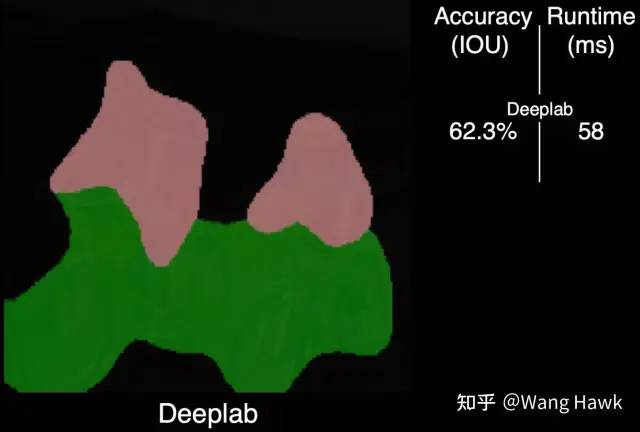
Deeplab語義分割結果 現在引入一個復雜的后處理算法DenseCRF, 可以得到下面的結果
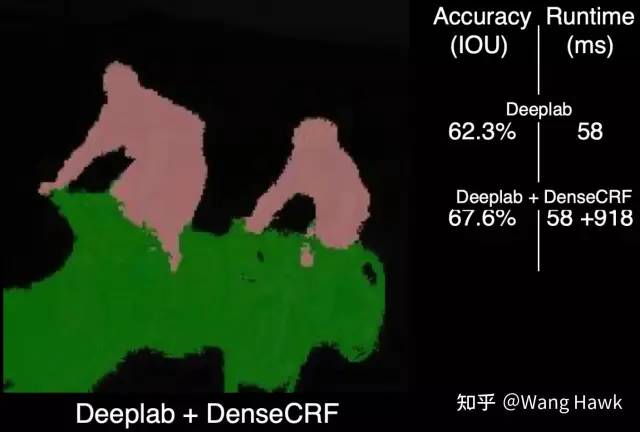
DenseCRF優化Deep Lab算法結果的展示 如果我們將DenseCRF替換為FBS加入到網絡中,可以看到效果相似,但速度是11倍快!
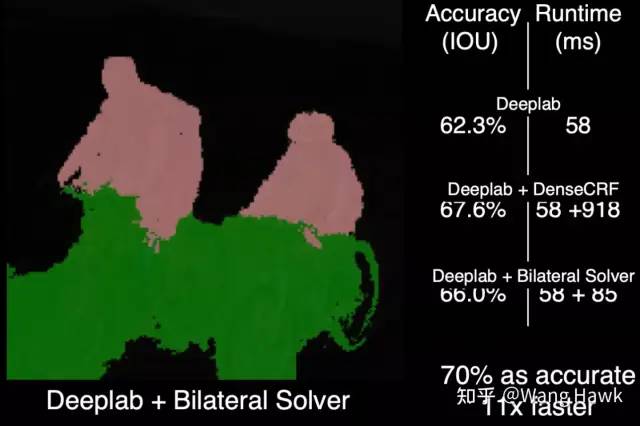
FBS優化Deep Lab算法結果的展示
五. 總結
今天我為你介紹了Jon Barron的經典算法Fast Bilateral Solver,可以說這是我最喜歡的算法之一。其中包含了很多深邃的思想。 首先是對很多問題中輸出圖像特性的敏銳觀察,并把這種觀察表達為了優美的數學公式。這種思想,和我之前在文章50. 從暗通道先驗去霧到海底圖像修復-三維重建輔助計算攝影中介紹的何凱明的“利用暗通道先驗去霧”有異曲同工之妙。
輸出圖像的兩大特性 然后是作者將上述復雜的公式,轉換到了雙邊空間中,降低問題規模,用于快速求解,而在今天所說的FBS算法中,作者又將這種思想進行了更深層次的應用。

問題轉換求解空間 在求解問題的過程中,作者又高效的利用了級聯金字塔形式,并采用了一種特殊的共軛梯度法來求解,使得求解過程大大加速,并得到了更好的效果。講到這里不得不說作者的數學功底超級扎實,如果你看原文及作者的論文附件,一定會對文章中問題建立和問題優化的細致分析過程擊節而嘆!當然,讀懂這些分析過程還是很燒腦的,所以我準備在我的知識星球中仔細的對應著作者的代碼進行分析和注解,感興趣的朋友可以加我“計算攝影學”公眾號,進而了解星球的加入方法。 還有一點值得提的是, FBS在傳統算法和深度學習算法中都可應用,可以說是連接過去和現在的橋梁,所以后面很多人寫文章來描述如何將Fast Bilateral Solver的思想應用到深度學習算法中,感興趣的話你可以搜索一下。

反向傳播示例 不過,FBS也并非沒有缺陷。它最大的問題也就在于雙邊平滑權重是與輸入參考圖像高度相關上——這使得其最終效果很容易受到輸入參考圖像的影響,很容易在結果中引入輸入參考圖像本身的紋理。下圖中左下角是SGBM的結果,右下角是FBS處理后的結果。我們可以看到頭發部分的視差圖很明顯引入了原圖中美女頭發部分的紋理特征,這并非我們想要的結果。處理這樣的問題,需要我們在應用FBS的過程中,仔細的調整各個參數和輸入的置信度圖,并且選擇性的應用FBS在部分區域上,而不是一股腦用于全圖的所有像素上。

FBS容易引入參考圖像的紋理信息 總的來說,FBS是一種非常經典和優秀的通用圖像處理算法,當它應用到立體匹配的視差后處理時,能夠起到“化腐朽為神奇”的功效,非常值得學習!現在看看我們的進度吧,我們終于完成了經典視差優化算法的學習,即將邁入立體匹配的現代算法——基于深度學習的立體匹配算法部分,驚不驚喜,期不期待 就讓我們拭目以待吧!
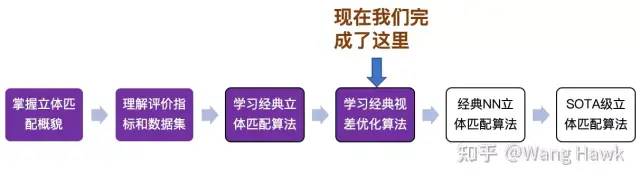
我們當前的進度
審核編輯 :李倩
-
算法
+關注
關注
23文章
4599瀏覽量
92643 -
函數
+關注
關注
3文章
4306瀏覽量
62431
原文標題:立體匹配:經典算法Fast Bilateral Solver
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
手寫圖像模板匹配算法在OpenCV中的實現

system_adc_read_fast為什么只能采集255個樣本?
機器學習的經典算法與應用

求助,為什么ble_mesh_fast_prov_server和ble_mesh_fast_prov_client運行之后沒能連接上呢?
ble_mesh_fast_prov_client在配網時不能支持PB-GATT嗎?
GPIO_MODE_OUT_OD_LOW_FAST和GPIO_MODE_OUT_OD_HIZ_FAST這兩個是什么區別呢?
系統分析大講堂:Clarity 3D Solver 課程新內容
十大排序算法總結
OpenCV邊緣模板匹配算法原理詳解





 立體匹配:經典算法Fast Bilateral Solver
立體匹配:經典算法Fast Bilateral Solver












評論