最近在研究三相逆變,寫(xiě)篇博客分享一下。
電路拓?fù)?/p>
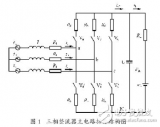
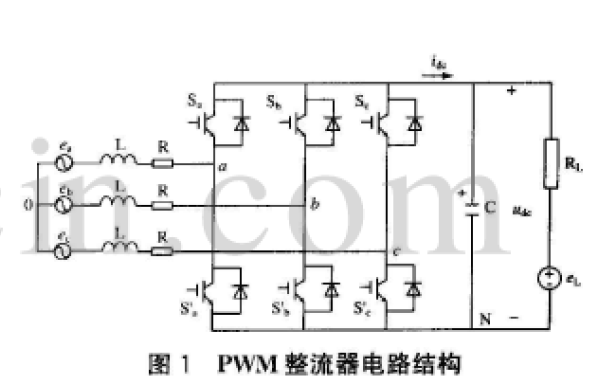
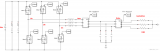
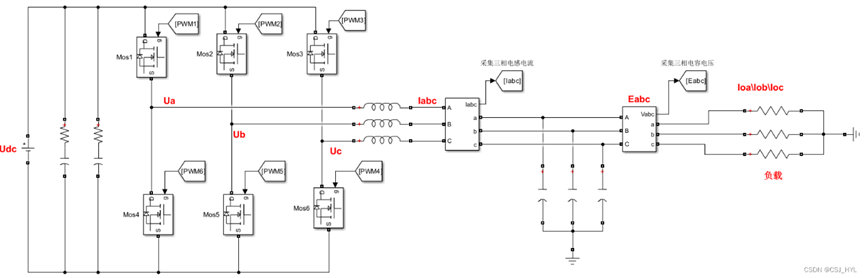
如下圖所示,為三相電壓型逆變電路的主電路拓?fù)洹V麟娐分饕伤牟糠纸M成,直流電源、6個(gè)開(kāi)關(guān)管(互補(bǔ)導(dǎo)通)、三個(gè)濾波電感和濾波電容組成的濾波電路、負(fù)載,實(shí)際上是三個(gè)星接的電阻。
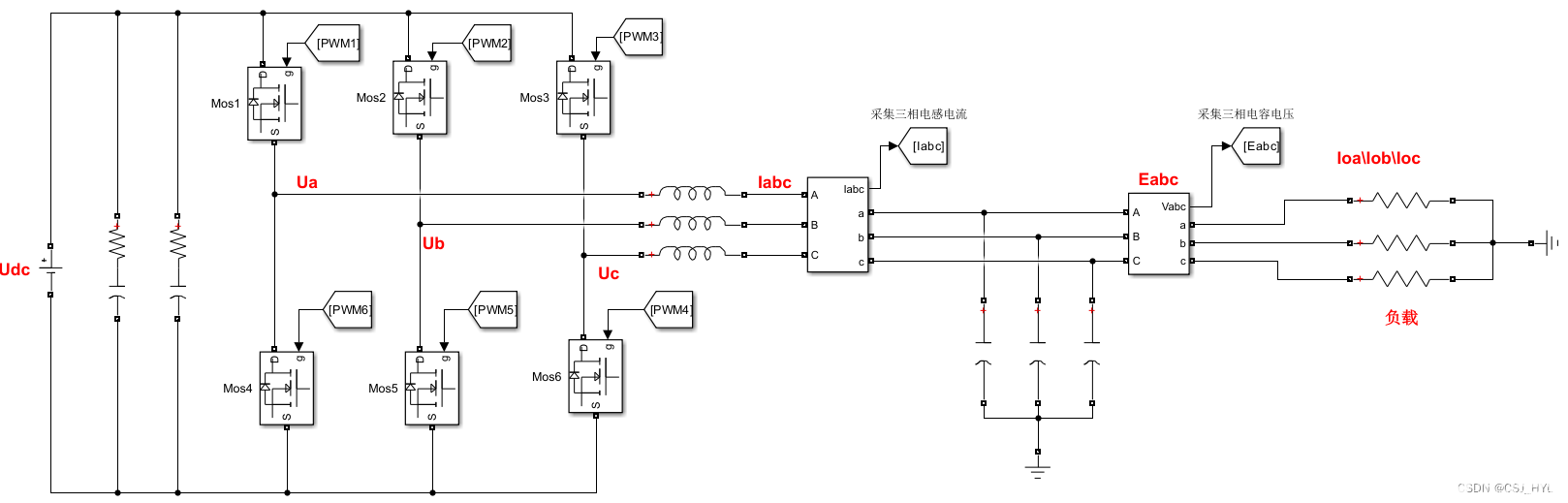
其中Udc表示直流側(cè)電壓,靠近直流側(cè)的兩個(gè)電容為輸入濾波電容,Ua、Ub、Uc表示為每個(gè)逆變橋臂的中點(diǎn)到直流測(cè)電壓負(fù)極,是逆變橋臂輸出的每相脈沖電壓,Ia、Ib、Ic表示為三個(gè)流經(jīng)濾波電感的相電流,Ea、Eb、Ec表示為電容電壓,也就是負(fù)載電壓。Ioa、Iob、Ioc表示為流經(jīng)負(fù)載的電流。
逆變器的數(shù)學(xué)模型
需要通過(guò)建立逆變器的數(shù)學(xué)模型來(lái)研究該電路,為下一步設(shè)計(jì)控制器打好基礎(chǔ)。分析這種電路,往往從電感、電容入手,根據(jù)KVL、KCL列寫(xiě)電路方程,進(jìn)而得到電路的數(shù)學(xué)模型。
2.1 逆變器在三相靜止坐標(biāo)系下的數(shù)學(xué)模型
根據(jù)KVL定理,可列出副邊abc三相的電壓回路方程,公式(2.1):
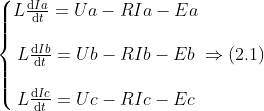
式中,R為相應(yīng)回路電感的等效阻值,Ua、Uc、Uc分別為a、b、c三相的相電壓,Ia、Ib、Ic為流經(jīng)電感的電流。
根據(jù)KCL定理,可以得出副邊電流的回路方程,公式(2.2)
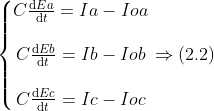
通過(guò)公式(2.1)、公式(2.2),我們就得到了該逆變器在三相靜止坐標(biāo)系下的數(shù)學(xué)模型。三相靜止坐標(biāo)系abc下的數(shù)學(xué)模型雖然能夠很好地買(mǎi)描述電壓和電流之間的關(guān)系,但是模型中有多個(gè)輸入、多個(gè)輸出,表達(dá)式和變量比較多,難以設(shè)計(jì)相應(yīng)的控制器。
2.2 逆變器在αβ軸坐標(biāo)系下的數(shù)學(xué)模型
通過(guò)Clack變換可以將模型簡(jiǎn)化,得到αβ正交坐標(biāo)系下的表達(dá)式。原理如下圖所示:
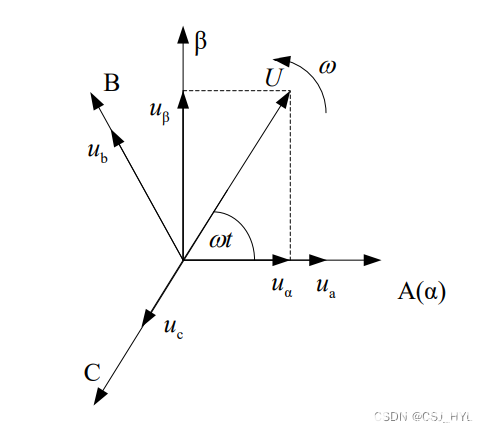
因?yàn)?Δ/Yo 變壓器的存在使原邊線電壓和為零,所以原邊不存在零序分 量,負(fù)載不平衡時(shí)作為擾動(dòng)考慮,因此暫不考慮零軸,對(duì)應(yīng)的變換關(guān)系為
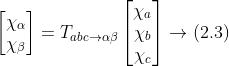
式中,變換矩陣
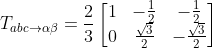 ?
?
編輯。乘以2/3是因?yàn)樽龅氖堑入妷旱淖儞Q,原以是合成后的αβ軸的分量最大值是abc靜止坐標(biāo)系的3/2倍。還有一種變換類(lèi)型是等功率的變換,這里不做講述。
將式(2.1)、(2.2)、(2.3)聯(lián)立,可以得出對(duì)應(yīng)在αβ坐標(biāo)系的方程,式(2.4)
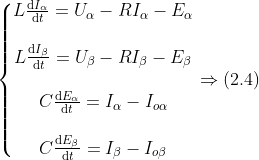
經(jīng)過(guò)Clack變換后,減少了控制變量,簡(jiǎn)化了控制系統(tǒng)。并且αβ分量相互獨(dú)立,沒(méi)有耦合在一起,控制起來(lái)比較方便。但是傳統(tǒng)的PI控制器對(duì)于追蹤交流量效果并不好,會(huì)有靜態(tài)誤差產(chǎn)生。但對(duì)于直流量并不會(huì)產(chǎn)生靜態(tài)誤差,所以說(shuō)還要進(jìn)行Pack變換,將式(2.4)轉(zhuǎn)換到dq坐標(biāo)系下。
2.3 逆變器在dq軸坐標(biāo)系下的數(shù)學(xué)模型
將兩相靜止αβ 坐標(biāo)系中的變量變換到兩相旋轉(zhuǎn) dq 坐標(biāo)系中稱(chēng)為 Park 變換,其原理如下圖所示。
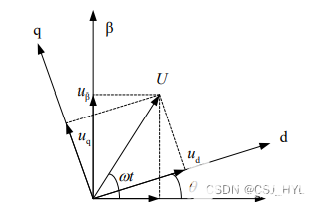
定義Park變換矩陣為,Cpark可以得到如下式(2.5)所示的關(guān)系。
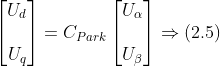
中,變換矩陣
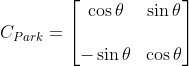
通過(guò)聯(lián)立式(2.4)、(2.5)可以得到對(duì)應(yīng)在dq軸坐標(biāo)系下的數(shù)學(xué)模型,表達(dá)式為:
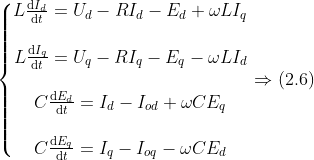
通過(guò) Park 變換可將數(shù)學(xué)模型轉(zhuǎn)換到旋轉(zhuǎn)坐標(biāo)系下。因?yàn)樽鴺?biāo)系與參考旋轉(zhuǎn)矢量的旋轉(zhuǎn)的方向還有速度是相同的,所以它們兩個(gè)是相對(duì)靜止,在旋轉(zhuǎn)坐標(biāo)系下為直流量, 能夠簡(jiǎn)化數(shù)學(xué)模型,使控制更容易實(shí)現(xiàn)。

3.逆變器的等效電路模型
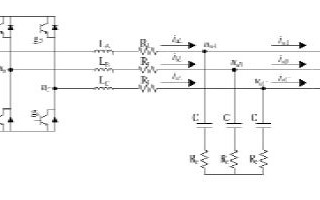
在張興的《PWM整流器》這本書(shū)中寫(xiě)到了這種等效變壓器模型電路。
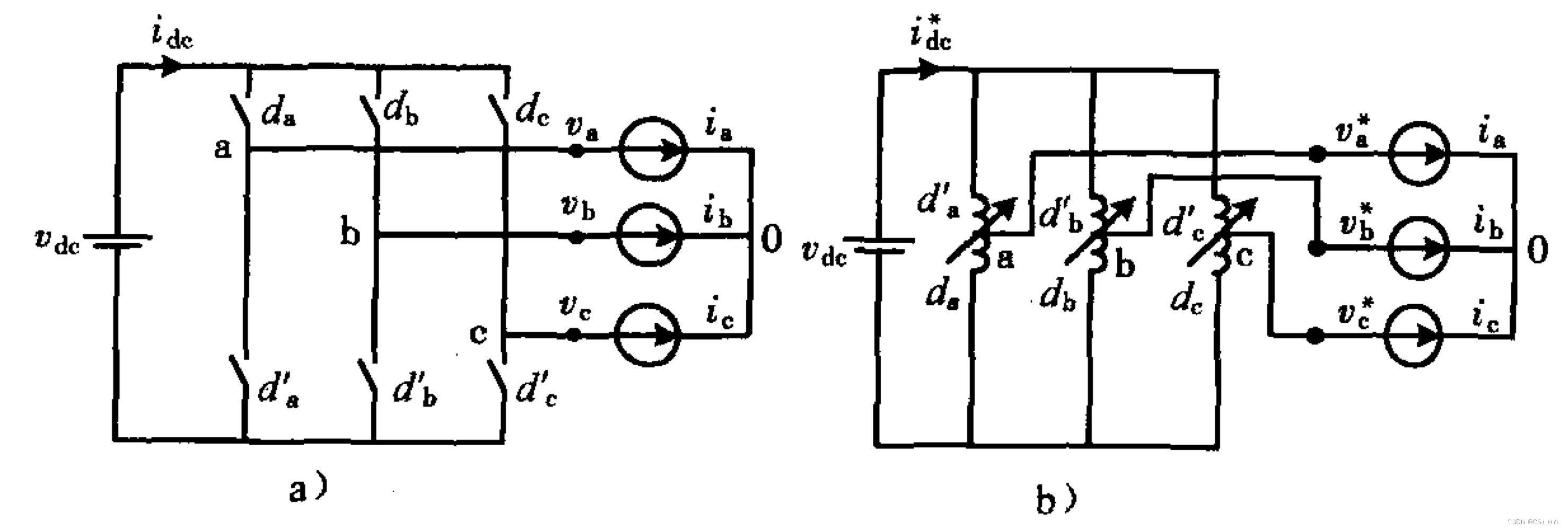
這里的da、db、dc、da'、db'、dc'表示的是對(duì)應(yīng)開(kāi)關(guān)管的PWM占空比,可以用自耦變壓器來(lái)代替開(kāi)關(guān)管,進(jìn)而得出變壓器模型 。
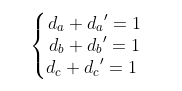
通過(guò)前面得出的dq坐標(biāo)系下的數(shù)學(xué)模型,進(jìn)一步可以得到dq坐標(biāo)系下的變壓器模型。通過(guò)這種模型可以幫助我們更好的去理解dq坐標(biāo)系下的數(shù)學(xué)模型。
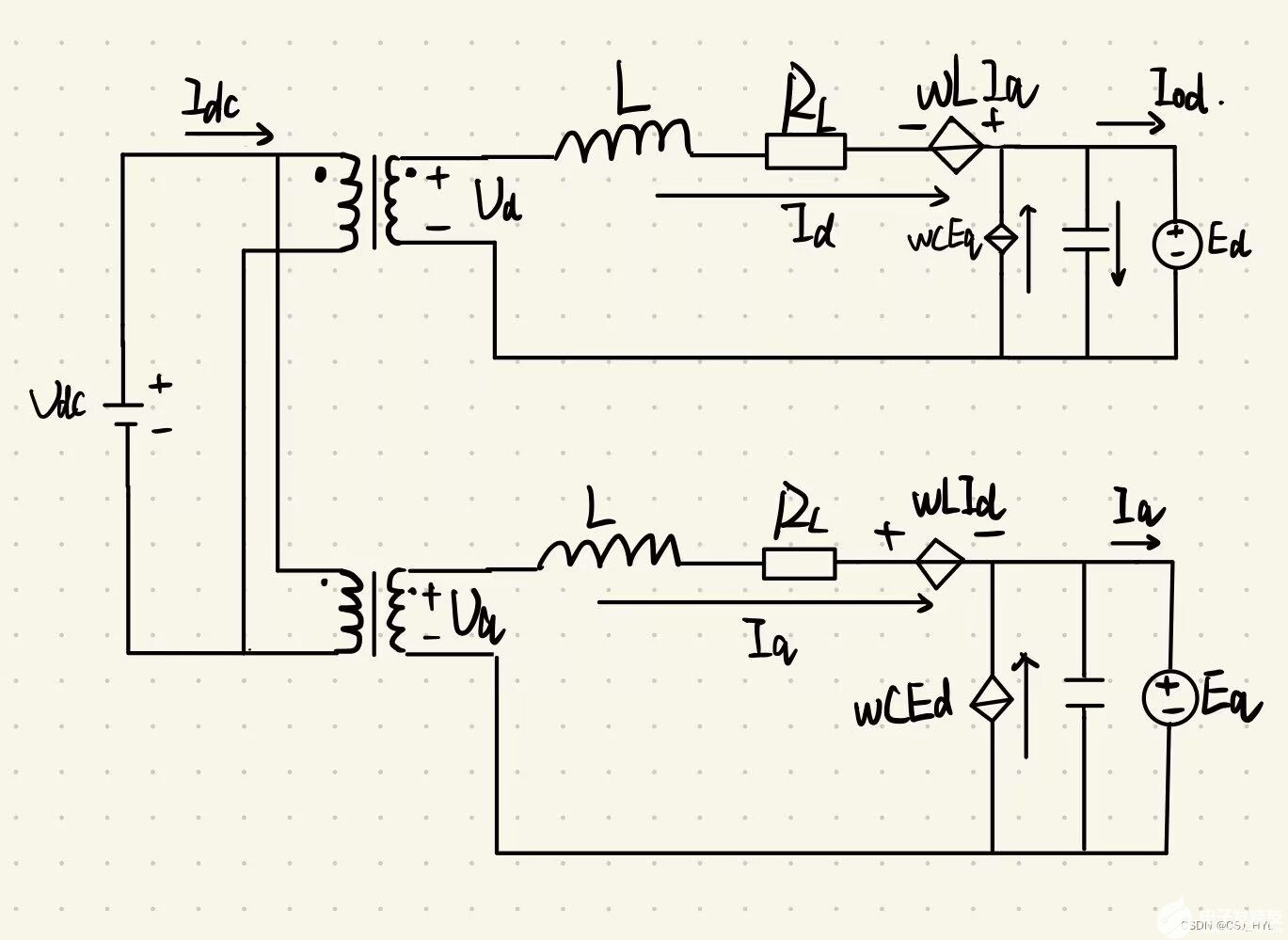
圖畫(huà)的不是太好
4.小結(jié)
通過(guò)以上變換得到了逆變器在不同坐標(biāo)系下的數(shù)學(xué)模型,為控制器的設(shè)計(jì)打下了良好的基礎(chǔ)。實(shí)際上控制器是按照dq坐標(biāo)系下建立數(shù)學(xué)模型。
這里在建立數(shù)學(xué)模型的時(shí)候并沒(méi)有去考慮調(diào)制的方法,實(shí)際上調(diào)制的方法是用來(lái)產(chǎn)生Ua,Ub、Uc的,完成建立數(shù)學(xué)模型并且完成設(shè)計(jì)控制器,我們就能得到目標(biāo)的Ua,Ub、Uc,然后根據(jù)目標(biāo)的Ua,Ub、Uc去調(diào)制,輸出PWM,來(lái)產(chǎn)生原邊電壓,進(jìn)而達(dá)到我們的控制要求。
還有一點(diǎn)就是這里的變換是通過(guò)矩陣的形式,在坐標(biāo)系轉(zhuǎn)換的運(yùn)算過(guò)程中也是通過(guò)矩陣運(yùn)算來(lái)實(shí)現(xiàn)的。
例如:
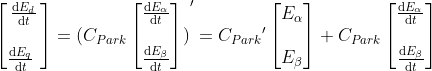
其中,
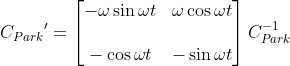
審核編輯:湯梓紅
-
逆變器
+關(guān)注
關(guān)注
279文章
4549瀏覽量
203928 -
逆變電路
+關(guān)注
關(guān)注
19文章
294瀏覽量
39288 -
SVPWM
+關(guān)注
關(guān)注
14文章
611瀏覽量
90414 -
數(shù)學(xué)模型
+關(guān)注
關(guān)注
0文章
79瀏覽量
11897
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
永磁同步電機(jī)控制系列的數(shù)學(xué)模型(7):怎么解耦

三相逆變器電壓閉環(huán)控制仿真
simulink中pmsm的數(shù)學(xué)模型及坐標(biāo)變換總結(jié)
基于分類(lèi)算法的雙三相感應(yīng)電機(jī)SVPWM
【下載】《現(xiàn)代永磁同步電機(jī)控制原理及MATLAB仿真》——同步電機(jī)MATLAB仿真與技術(shù)分析
三相電壓型整流器數(shù)學(xué)模型及其控制算法的研究
如何設(shè)計(jì)具有前饋解耦控制的PWM整流器雙閉環(huán)控制系統(tǒng)及仿真資料說(shuō)明
采用雙閉環(huán)PI和重復(fù)控制方案實(shí)現(xiàn)三相逆變器設(shè)計(jì)并進(jìn)行仿真分析
三相電壓型逆變器電壓閉環(huán)控制的Simulink仿真資料免費(fèi)下載

基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(2)--控制器設(shè)計(jì)
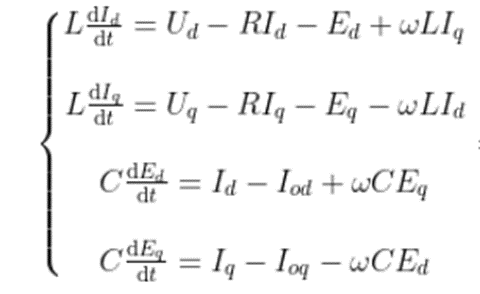
基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器之仿真驗(yàn)證

三相SVPWM電壓型逆變器的數(shù)學(xué)模型




 基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(1)--數(shù)學(xué)模型
基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(1)--數(shù)學(xué)模型










評(píng)論