【動(dòng)態(tài)電路】的零狀態(tài)響應(yīng)就是電路在零初始狀態(tài)下(動(dòng)態(tài)元件初始儲(chǔ)能為零),由外施激勵(lì)源引起的響應(yīng),與零輸入響應(yīng)不同的是,零狀態(tài)響應(yīng)內(nèi)部儲(chǔ)能在初始狀態(tài)是零,就是儲(chǔ)能元件初始儲(chǔ)能為零,區(qū)分好這個(gè)后,就可以方便記住了,這期介紹RC電路的零狀態(tài)響應(yīng),同樣需要點(diǎn)一階線性微分方程的基礎(chǔ)!
關(guān)鍵詞:RC電路;零狀態(tài)響應(yīng);
01電路結(jié)構(gòu)
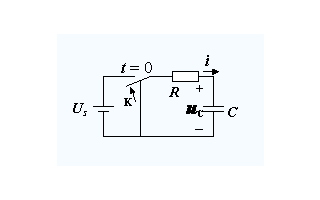
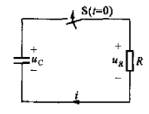
如圖1-1所示,是RC電路的結(jié)構(gòu):
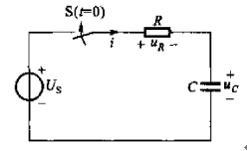
圖1-1 RC電路零狀態(tài)響應(yīng)電路結(jié)構(gòu)
圖1-1中,開關(guān)S閉合前,電容C沒有充電,其電容電壓為0,得已知條件為:
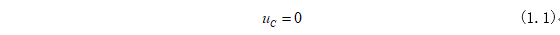
02分析思路
開關(guān)S閉合后,電容儲(chǔ)存得能量將通過電阻以熱能得形式釋放出來,以開關(guān)動(dòng)作為(t=0),那么開關(guān)閉合后,根據(jù)KVL可得:
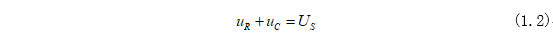
其中電阻電壓和電容電流為:
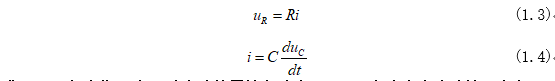
式(1.4)與上期那個(gè)一階電路的零輸入響應(yīng)——RC電路中電流計(jì)算沒有負(fù)號(hào)的原因是,圖1-1電路電容電壓為上正下負(fù),電流i流進(jìn)電容,給電容充電,上期電路相反,電流流出電容,電容充當(dāng)電源。
將式(1.3)和式(1.4)代入式(1.2)可得電路的微分方程為:
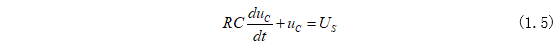
式(1.6)是一階線性非齊次方程,方程的解由非齊次方程的特解和對(duì)應(yīng)齊次方程的通解兩個(gè)分量組成,這個(gè)在“重拾數(shù)學(xué)基礎(chǔ)”中進(jìn)行講解了,忘記了可以再返回去看看!
其求解公式為:
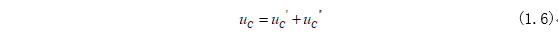
式(1.6)中等式右邊第一項(xiàng)是非齊次方程的特解,第二項(xiàng)是齊次方程的通解。特解可以通過初始條件(1.1)代入式(1.5)可以求得非齊次方程的特解為:
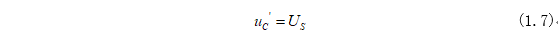
而齊次方程可根據(jù)上期“一階電路的零輸入響應(yīng)——RC電路”的通解為:
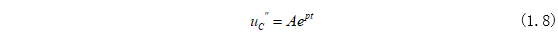
將式(1.8)中系數(shù)P換成時(shí)間常數(shù)為:
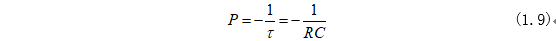
式(1.9)時(shí)間常數(shù)為RC,因此式(1.8)變?yōu)椋?/p>
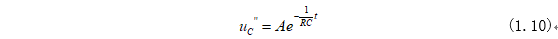
因此式(1.6)可根據(jù)式(1.8)和式(1.7)求得為:
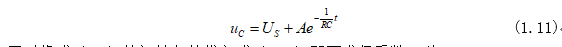
同時(shí)將式(1.1)的初始條件代入式(1.11)即可求得系數(shù)A為:
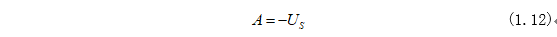
將式(1.12)代入式(1.11)因此式(1.11)可為:
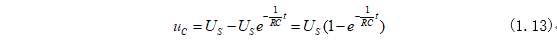
將電容電壓進(jìn)行求導(dǎo)即可求得電容電流i為:
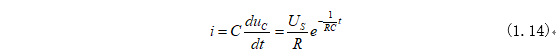
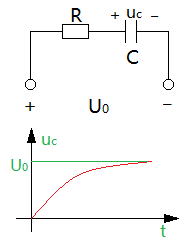
電路中電壓、電流的波形如圖1-2所示:
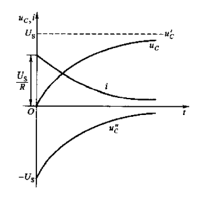
圖1-2 電路電壓、電流波形
圖1-2說明,電容電壓以指數(shù)形式趨近于它的最終恒定值Us,到達(dá)該值后,電壓和電流不再變化,電容相當(dāng)于開路,電流為零,此時(shí)電路達(dá)到穩(wěn)定狀態(tài)。RC電路接通直流電壓源的過程也即是電源通過電阻對(duì)電容進(jìn)行充電的過程。
-
RC
+關(guān)注
關(guān)注
0文章
225瀏覽量
48763 -
動(dòng)態(tài)電路
+關(guān)注
關(guān)注
1文章
27瀏覽量
9574 -
一階電路
+關(guān)注
關(guān)注
0文章
30瀏覽量
13199 -
RC電路
+關(guān)注
關(guān)注
2文章
161瀏覽量
30196 -
零狀態(tài)響應(yīng)
+關(guān)注
關(guān)注
0文章
8瀏覽量
666
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
論全響應(yīng)和零狀態(tài)響應(yīng)、零輸入響應(yīng)
RC一階電路的響應(yīng)測試
RC一階電路的響應(yīng)測試
零輸入響應(yīng)與零狀態(tài)響應(yīng)分析
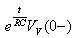
一階電路的零狀態(tài)響應(yīng)
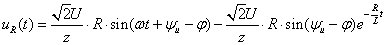
一階RC電路的零輸入響應(yīng)與零狀態(tài)響應(yīng)的電路分析基礎(chǔ)實(shí)驗(yàn)資料免費(fèi)下載
RC電路與RL電路是如何響應(yīng)的
淺談RC電路的零狀態(tài)響應(yīng)
講解RC電路的零輸入響應(yīng)




 講解RC電路的零狀態(tài)響應(yīng)
講解RC電路的零狀態(tài)響應(yīng)










評(píng)論