概述:本文詳細介紹了CRC循環冗余計算的數學原理,算法中使用的參數說明,并以Modbus協議中的CRC-16算法為例,進行手算驗證,同時提供LabVIEW和C語言的直接計算CRC-16 值的代碼以及C的查表計算CRC-16代碼和代碼原理的說明。
一、筆者個人經歷
初次接觸CRC校驗是因為項目需要上位機軟件來記錄PLC寄存器中的數據,實現PLC控制全過程中關鍵數據的記錄和查詢。上位機軟件使用LV進行編寫,數據的獲取通過Modbus TCP實現,因為當時對Modbus和CRC都不是很熟悉,就采用了最成熟簡單的辦法,直接調用了第三方的Modbus工具包,項目功能也是順利實現。之后又遇到一個項目,需要上位機作為從機,回應主控的Modbus RTU指令,這次沒有選擇直接使用Modbus工具包,而是使用《LabVIEW寶典》中Modbus CRC-16校驗算法,根據Modbus RTU協議自主編程完成了項目要求。后來因為做嵌入式單片機,又了解使用了CRC-8和CRC-16的查表算法,也是沒有詳細了解過CRC循環冗余校驗的原理,僅僅是可以熟練實現功能。直到后來遇到一個項目,需要用示波器捕捉并分析出未知的通信幀的通信協議,幀頭,幀尾很快通過對比分析了出來,通信內容也是反復實驗分析出具體數據字節和位的意義,就是校驗方式分析不出,但是可以肯定數據幀是一定包含校驗字節的,那時才認真開始考慮CRC循環冗余算法,試圖找出數據幀的校驗規則,很慚愧沒有分析出來,后來是通過第三方的幫助才解決了這個問題,但是當時腦中留下了很多問號和片段式的思考及部分無序的筆記,現在重新進行了整理、思考和驗證,形成此文,希望可以解答對CRC循環冗余校驗算法有疑問的同學的困惑。
二、CRC循環冗余校驗原理
百度CRC可以很容易的獲取CRC的定義:CRC(Cyclic Redundancy Check),即循環冗余校核,是一種根據網絡數據包或電腦文件等數據產生簡短固定位數校核碼的快速算法,主要用來檢測或校核數據傳輸或者保存后可能出現的錯誤。CRC利用除法及余數的原理,實現錯誤偵測的功能,具有原理清晰、實現簡單等優點。
首先明確CRC是一種數據校驗方法,與和校驗、異或校驗功能相同,常用于通信的雙方判斷通信幀在通信過程中數據傳輸是否正確,如校驗不通過則需要考慮舍棄此通信幀,同時需根據需要判斷是否需要向發送方反饋通信異常的情況。
1、模2運算
從百度到的CRC定義中可以看到CRC是利用除法和余數的原理,這里所說的除法和余數的原理就是模2算法了,下面是模2算法的百度定義。
模2運算是一種二進制算法,CRC校驗技術中的核心部分。與四則運算相同,模2運算也包括模2加法、模2減法、模2乘法、模2除法四種二進制運算。與四則運算不同的是模2運算不考慮進位和借位,模2算術是編碼理論中多項式運算的基礎。模2算術在其他數字領域中的應用也是很廣泛的。
這里可以得出模2算法是不考慮進位和借位的,也就可以理解為每位都是獨立的,不會影響其他位也不會被其他位影響,這點在后文中的計算驗證部分有體現。
下面是模2運算的四則運算法則:
0+0=0;0+1=1;1+0=1;1+1=0;
0-0 =0;0-1=1;1-0=1;1-1=0;
0 *0=0;0 *1=0;1*0=0;1*1=1;
0/1=0; 1/1=1;
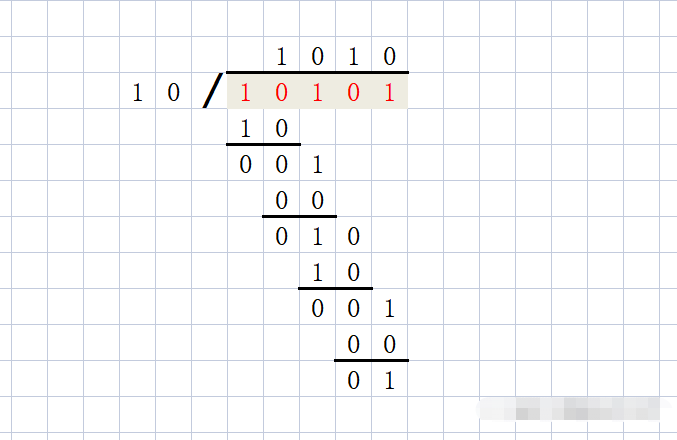
CRC算法中主要使用到的就是模2減法和模2除法。通過上述模2減法法則可以發現,模2減法實際和異或運算在結果上是完全相同的,也就不再過多描述。這里最關鍵的是多位二進制的除法,這是CRC校驗的核心部分。模2除法具有以下性質:
(1)每一位除的結果不影響其他位,即不向上一位借位;
(2)當被除數的位數小于除數位數時,則商為0,被除數就是余數,也可以理解為被除數首位為0時,商為0。
(3)只要被除數的位數和除數一樣多,且最高位為1,不管其他位是什么數,皆可商1,也可以理解為被除數首位為1,商為1,余數為被除數與除數的模2減的結果;
(4)要保證每次除完首位都為0,才能進行右移;
(5)當最后余數的位數小于除數位數時,除法停止。
通過對上述多位二進制的模2除法性質的思考,我們可以感覺到模2除與循環異或的本質是相同的,這個可以通過下文中具體的計算過程體現。
2、CRC算法參數
這里給大家推薦一個很好用的CRC計算工具:
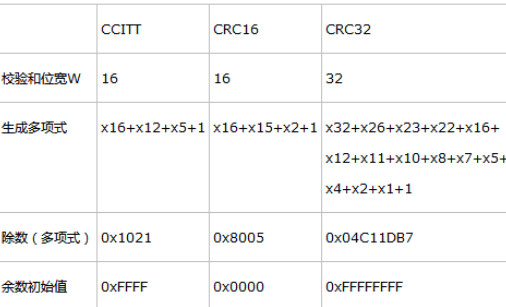
,這個計算工具包含了很多種CRC算法,并且標示出了具體的關鍵參數,從我個人的使用經歷上來說,需要注意的就僅僅是CRC-16 Modbus的計算結果是高字節在前,低字節在后的,這個與實際使用中通常低字節在前高字節在后不同,需要注意一下。下面我們就以CRC-16 Modbus為例對CRC算法進行說明。

(1)標準CRC生成多項式
每種CRC算法的標準生成多項式可能是不同的,這個需要進行注意。從上面截圖的左下方我們可以得知,CRC-16 Modbus的標準生成多項式是X16+X15+X2+1,其中1可以換成X0,這樣就很容易可以看出,16、15、2、0這些數字代表的是多位二進制數的數位,則標準生成多項式可寫為1 1000 0000 0000 0101,對應十六進制就是0x18005,也就是對應上圖右側的Poly:0x8005。這里的0x8005實際是標準生成多項式的簡記式,因為標準生成多項式的最高位固定為1,故在簡記式中就忽略了最高位1了,同時在程序編程中實際使用的也是簡記式,這個在下文的程序部分有所體現。
(2)CRC初始值
初始值,這個也是根據具體哪種CRC標準來確定的,不同的CRC標準對應不同的計算初始值。還是以CRC-16 Modbus為例,計算初始值就是0xFFFF,對應上圖Init:0xFFFF。計算初始值先與需要校驗的數據的首字節數據進行異或,異或后結果進行模2除法運算,這個后續程序部分會體現。
(3)正序/反序
就像串口通信需要考慮低位先傳還是高位先傳一樣,循環冗余計算時也需要考慮從高位開始還是低位開始,即編程時需要考慮數據進行左移還是右移。需要說明的一點是,數據進行正序或者反序,最后的結果是不相同的,這個下文也會進行驗證說明。上圖計算工具中是通過RefIn和RefOut來進行體現的。
RefIn:true或false表示在進行計算之前,原始數據是否翻轉,如原始數據:0x34 = 0011 0100,如果REFIN為true,進行翻轉之后為0010 1100 = 0x2C。
REFOUT:true或false表示運算完成之后,得到的CRC值是否進行翻轉,如計算得到的CRC值:0x97 = 1001 0111,如果REFOUT為true,進行翻轉之后為1110 1001 = 0xE9。
以CRC-16 Modbus為例,都是True,則表示反序循環冗余校驗。這個結合下文程序會更好理解,下文也會進行相應的說明。
(4)CRC結果異或值
CRC結果異或值就是CRC循環冗余計算的結果與CRC結果異或值進行異或處理,結果為CRC計算的最終值,對應上圖中的XorOut:0x0000。
3、手算CRC算法及驗證
前面已經介紹了模2算法以及CRC算法的參數,下面就來驗證一下上面的理論是否正確。還是以CRC-16 Modbus為例,對單字節0x12數據計算校驗值。
首先需要確定CRC-16 Modbus算法的參數:
(1)標準生成多項式為X16+X15+X2+1,轉換成二進制則為1 1000 0000 0000 0101;
(2)初始值為0xFFFF;
(3)采用反序的計算順序;
(4)CRC結果異或值為0x0000;
然后就按照CRC-16 Modbus算法來進行計算,
0x12轉為二進制為0001 0010;
與0xFFFF即1111 1111 1111 1111異或,結果為1111 1111 1110 1101;
反序為1011 0111 1111 1111;
下面進行模2除,被除數為1011 0111 1111 1111 0000 0000,除數為1 1000 0000 0000 0101,因為通信幀的基本單位是字節,所以被除數為1011 0111 1111 1111后面加8個0。

模2除余數為1111 1100 1011 0010;(這里需要注意一下,CRC循環冗余算法中關注的是模2除的余數,而不是商)
反序為0100 1101 0011 1111,即0x4D3F;
結果再與0x0000進行異或,最終結果為0x4D3F。
利用上面介紹的CRC計算小工具進行驗證,結果如下圖所示。

同理,筆者針對不同標準生成多項式進行手算實驗,選擇了CRC-32 對0x12進行CRC校驗,手算結果與CRC計算工具結果相同。
同時針對數據的正序反序問題,選擇CRC-8對0x12進行CRC校驗,手算結果與CRC計算工具結果相同。
對于多字節數據的校驗過程是:首先首字節與初始默認值進行異或校驗,結果作為被除數進行模2除法;下一個字節與上一個字節的模2除法的結果進行異或,作為下一次模2除法的被除數;以此類推,這個在下文代碼部分體現。
筆者針對多字節也進行了手算實驗,選擇了CRC-16 Modbus對0x12、0x34兩個字節進行了CRC校驗,手算結果與CRC計算工具結果相同。
三、CRC 編程實現方法
1、直接計算法
CRC算法這里還是以CRC-16 Modbus為例,其直接計算編程實現過程為:
1)設置CRC寄存器,并給其賦值0xFFFF。
2)將數據的第一個8-bit字符(將此8位高位補0為16位)與16位CRC寄存器的值進行異或,并把結果存入CRC寄存器。
3)CRC寄存器向右移(即最低位方向)一位,MSB補零,移出并檢查LSB。
4)如果LSB為0,重復第三步;若LSB為1,CRC寄存器與多項式碼(0xA001)相異或。此時的0xA001即為0x8005的反序。
注意:該步檢查LSB應該是右移前的LSB,即第3步前的LSB。
5)重復第3與第4步直到8次移位全部完成。此時一個8-bit數據處理完畢。
6)重復第2至第5步直到所有數據全部處理完成。
7)最終CRC寄存器的內容即為CRC值。
這里對上文中提及的標準多項式和簡記式的區別再進行一下說明:
在上文中手算部分可以看到實際標準多項式最高位對應被除數的那一位必定是1,與標準多項式最高位異或的結果或者說模2減的結果必定是0,因此,在步驟4)就是僅判斷LSB是1還是0,進而確定是先進行異或再移位還是直接進行移位,而不參與異或運算,同時也可以理解上述步驟中僅涉及簡記式進行異或或者說模2減。
讀者可以結合上文中的手算部分的運算步驟來理解這里的處理步驟,關鍵是理解模2除和數據右移的關系,筆者這里不再進行過多說明。
LabVIEW直接計算 CRC-16 Modbus:

程序中while循環實際就是模2除法的體現,以下程序同理。
C語言直接計算CRC-16 Modbus:
unsigned short do_crc(unsigned char *ptr, int len)
{
unsigned char i;
unsigned int crc16 = 0xFFFF;
while(len--)
{
crc16 ^= *ptr++;
for (i = 0; i < 8; ++i)
{
if (crc16 &0x0001)
crc16 = (crc16 >> 0x01) ^ 0xA001;
else
crc16 = (crc16 >> 0x01);
}
}
return crc16;
}
這里有一點需要注意的是,返回的CRC16為16位數,分為兩個字節,高低字節需轉換(僅針對Modbus,因為modbus一般要求校驗值低位在前高位在后)。
2、查表法
對于查表法,其實就是利用空間換時間,通過直接查詢CRC運算結果表格來減少計算時間,這個在嵌入式單片機方面使用較多,這邊還是以CRC-16 Modbus為例。
首先針對表格進行說明:
因為標準生成多項式為X16+X15+X2+1,則可以確定校驗結果為2字節,因此表格分為高字節和低字節,高低位CRC數組中(即下面的 Table_CRCL[256] 和 Table_CRCH[256]中 )同下標的兩個單字節數組合成一個雙字節校驗值。
關于下面表格中數值,是使用CRC-16,(標準生成多項式為X16+X15+X2+1;初始值0x0000;RefIn:True,RefOut:True,即反序;XorOut:0x0000)計算的0-255的CRC值。例如0x01按照上述CRC算法,結果是0xC0C1,即對應Table_CRCH[1]=0xC0和Table_CRCL[1]=0xC1。這里讀者可能有疑問,為什么不是使用CRC-16 Modbus的算法?對比CRC-16 Modbus和上述算法的參數,可以看到僅僅是初始值不同,CRC-16 Modbus 初始值為0xFFFF。這里先明確,表的意義是取代模2除法的計算過程。
再回到之前的手算部分,即如下所示。

從上式可以發現,被除數從左邊起,8位及之后的7位,即1111 1111,這些數位僅參與異或且全程參與異或,或者說模2減,而異或是符合交換律的,即A^B^C=A^C^B,則1111 1111也可最后再參與異或,而0x00與任何單字節數異或均為單字節數本身,則上式被除數可以改成1011 0111 0000 0000 0000 0000 ,最后的余數低字節再與原被除數高字節異或,得到的數就是符合CRC-16 Modbus算法的最終的低字節值,也就是說原被除數高字節的值僅影響模2除余數的低字節值,這也就是下文代碼部分的解釋。
C語言查表計算CRC-16 Modbus:
const uint8_t Table_CRCL[256] = // CRC 高位字節值表
{
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1,
0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1,
0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1,
0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40,
0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1,
0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40
};
const uint8_t Table_CRCH[256] = // CRC高位位字節值表
{
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06,
0x07, 0xC7, 0x05, 0xC5, 0xC4, 0x04, 0xCC, 0x0C, 0x0D, 0xCD,
0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09,
0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A,
0x1E, 0xDE, 0xDF, 0x1F, 0xDD, 0x1D, 0x1C, 0xDC, 0x14, 0xD4,
0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3,
0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3,
0xF2, 0x32, 0x36, 0xF6, 0xF7, 0x37, 0xF5, 0x35, 0x34, 0xF4,
0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A,
0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29,
0xEB, 0x2B, 0x2A, 0xEA, 0xEE, 0x2E, 0x2F, 0xEF, 0x2D, 0xED,
0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26,
0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60,
0x61, 0xA1, 0x63, 0xA3, 0xA2, 0x62, 0x66, 0xA6, 0xA7, 0x67,
0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F,
0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68,
0x78, 0xB8, 0xB9, 0x79, 0xBB, 0x7B, 0x7A, 0xBA, 0xBE, 0x7E,
0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5,
0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71,
0x70, 0xB0, 0x50, 0x90, 0x91, 0x51, 0x93, 0x53, 0x52, 0x92,
0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C,
0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B,
0x99, 0x59, 0x58, 0x98, 0x88, 0x48, 0x49, 0x89, 0x4B, 0x8B,
0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42,
0x43, 0x83, 0x41, 0x81, 0x80, 0x40
};
uint16_t CRC16(uint8_t *puchMsg, uint8_t DataLen)
{
uint8_t CRCH= 0xFF ; // 高CRC字節初始化
uint8_t CRCL = 0xFF ; // 低CRC 字節初始化
uint8_t Index ; // CRC表中的索引
while (DataLen--)
{
Index = CRCL ^ *puchMsg++ ;
CRCL = CRCH ^ CRCL[Index];
CRCH = CRCH[Index];
}
return ((uint16_t)CRCL<< 8 | CRCH); // Modbus校驗值一般低字節在前,高字節在后
}
四、總結
本文選擇以CRC-16 Modbus算法標準進行了詳細的舉例及手算驗證,同時筆者也對比其他算法,如CRC-8,CRC-32進行了針對性的驗證,結果均證明正確。之所以選擇CRC-16 Modbus,感覺這個可能是大家平時使用中較為常用的,尤其是工控領域,同時也相信讀者舉一反三的能力,可以按照本文介紹方法掌握其他CRC算法。本文編寫期間也是對文字,計算及代碼反復考量驗證,力求正確性和邏輯性,轉發及引用請注明出處。
——文章來自宋雨的個人分享
審核編輯:湯梓紅
-
LabVIEW
+關注
關注
1963文章
3652瀏覽量
322393 -
crc
+關注
關注
0文章
199瀏覽量
29433 -
C語言
+關注
關注
180文章
7598瀏覽量
136178 -
代碼
+關注
關注
30文章
4744瀏覽量
68345 -
循環冗余校驗
+關注
關注
0文章
7瀏覽量
6532
發布評論請先 登錄
相關推薦
PSoC 4 循環冗余校驗 (CRC)
CRC循環冗余校驗的算法
循環冗余校驗碼---CRC碼
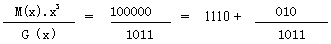
crc循環冗余校驗碼算法





 從原理到代碼理解CRC循環冗余校驗
從原理到代碼理解CRC循環冗余校驗











評論