了解如何使用拉普拉斯變換、Python 和 SymPy 以串聯 RLC 電路為例簡化電路分析的數學運算。
研究電路可能是一個非常滑坡。 在不知不覺中,你已經深入微分方程了。 對于那些對微積分感到不舒服的人來說,這可能是可怕的。 然而,我經常告訴我的EE學生,成為一名工程師并不是要善于以困難的方式解決難題; 相反,它主要是關于找到更簡單的方法來解決這些問題。 當我教授電路分析課程并需要激勵他們學習
拉普拉斯變換。
將隨時間變化的微分方程轉換為拉普拉斯空間可確保將這些微分方程的解簡化為代數練習; 不需要微積分! 然而,有時確定解決方案所涉及的代數量可能會抵消該方法的好處,使學生希望他們正在做更高級的數學。 然而,一種解決方案是
蟒。 利用Python可以大大減少確定解決方案所需的代數量。
在本文中,我們將首先通過一個例子,展示拉普拉斯空間是如何發揮作用的,以及 Python 如何幫助更輕松地完成數學。
示例:查找串聯RLC電路中的電流
在進入拉普拉斯空間和Python如何在電路分析中發揮作用之前,讓我們將示例設置到拉普拉斯變換進入的位置。
首先,考慮電流如何流過 電容器 與該電容器兩端的電壓與時間有關的導數成正比。 同樣,兩端的電壓 感應器
與流過該電感器的電流與時間有關的導數成正比:
等式 1a.
等式 1b.
這些差分關系對于描述和分析電路中的電流和電壓行為至關重要,如圖1所示。
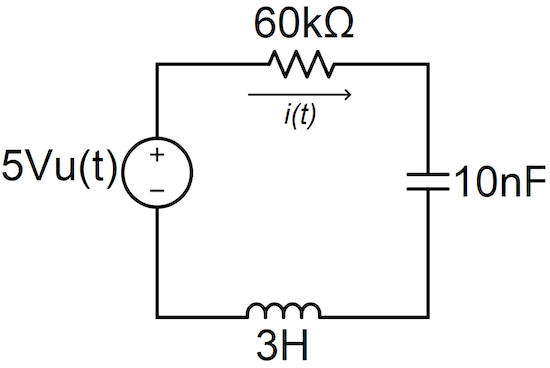
圖1. RLC電路示例。
在 RLC電路 在圖 1 中,我們看到流過元件的電流都是相等的,因為這些元件都是串聯的。 此外,在t ≥ 0時,該電路無源元件兩端的電壓等于5V(直流電源電壓)。 我們可以將這些關系寫成等式 2 和 3。
iL=iC=iRiL=iC=iR等式 2.
將等式1a和1b與等式2和3相結合,得到等式4,這是一個積分微分方程,描述了流過圖1所示電路的電流的時間行為。
等式4.
取公式4中關于時間的兩邊的導數,并重新排列微分項的系數,得到公式5,即描述圖1電路中電流瞬態行為的微分方程。
等式5.
讓我們停下來反思一下我們剛剛做了什么。 到目前為止,我們還沒有真正需要做太多的微積分。 基本上,我們已經描述了該電路中隨時間推移的電流演變,但我們還沒有解決該電流的功能形式。 如果我們要在時域中進行,我們需要確定該電路是過阻尼、欠阻尼還是臨界阻尼。 然后,為我們的解選擇了一個一般形式,我們需要將該一般解及其導數應用邊界條件,以確定解的一般形式的幾個常數值。
如果我們停留在時域中,這是求解二階電路中電流的最簡單、最直接的方法。 但是,如果我們將方程6轉換為拉普拉斯空間,我們可以避免時域的混亂(即大部分實際微積分)。
L{f(t)}=F(s)=∫∞0?f(t)e?stdtL{f(t)}=F(s)=∫0?∞f(t)e?stdt等式 6.
現在我們已經在示例中達到了這一點,讓我們簡要概述一下拉普拉斯空間。
拉普拉斯空間 - 拉普拉斯變換屬性和對
在這一點上,根據您的教育背景(或您對大學課程的褪色記憶),您可能想知道,“什么是拉普拉斯空間? 我將把更完整的描述留給數學家,但出于我們的目的,你可以把拉普拉斯空間想象成一個復雜的頻域。 拉普拉斯空間中的函數包含有關隨時間變化的豐富信息,可以使用簡單的代數來操作這些信息來提取該時間信息。
單側拉普拉斯變換通常根據公式6通過積分進行。 該方程定義了f(t),F(s)的拉普拉斯變換,作為f(t)和e乘積積分的結果-圣從 t = 0-到無窮大。 此外,根據公式7進行從s空間到時域的逆變換。
L?1{F(s)}=f(t)=12πj∫ε+j∞ε?j∞F(s)estdsL?1{F(s)}=f(t)=12πj∫ε?j∞ε+j∞F(s)estds等式7.
你總是可以執行這些積分從 s 空間變換到 t 空間,然后再變換回來,但積分是一種痛苦,逆拉普拉斯變換積分要求我們確保 ??
的值位于該積分的收斂區域內; 我們真的應該撣去我們復雜的分析技能,以正確執行這個積分。 幸運的是,拉普拉斯變換和逆變換通常可以使用拉普拉斯空間的線性屬性表和引用變換對表來執行,而無需完全積分。
圖2a和2b顯示了這些的最小版本,盡管可以通過互聯網搜索找到更完整的拉普拉斯表。
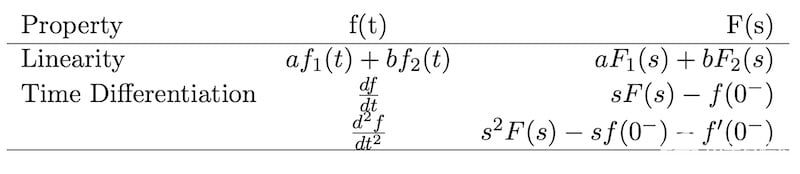
圖 2a. 拉普拉斯變換屬性。
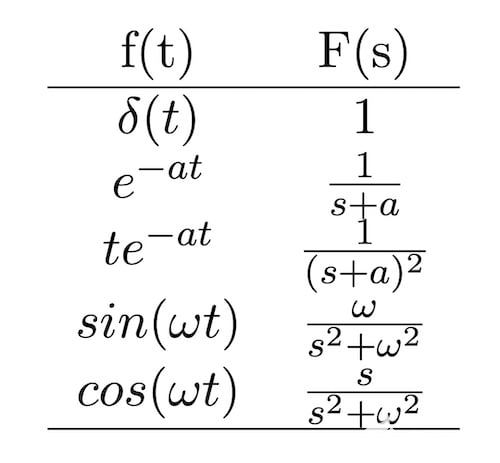
圖 2b. 拉普拉斯變換對。
現在我們已經有了復習,讓我們回到我們的示例。
求解拉普拉斯空間中的電流
將拉普拉斯變換屬性應用于時間相關方程 6 的每個項,可得出 s 空間方程 8。 重要的是要注意,我在這里假設t =
0之前的電流是0A,并且已經有一段時間了。
等式8.
考慮到這一點,我們可以輕松地代數操作方程9以找到I(s)。 然后,確定 i(t) 就像逆變換 I(s)一樣簡單。 這種簡單性是我們在拉普拉斯空間中進行電路分析的原因; 這是解決難題的一種非常快速的方法。
等式9.
從這里開始,事情可能會變得有點混亂。 的確,我們可以通過反轉用于使用圖 2 中的表從時域轉換到 s 空間的過程來執行逆變換。 但是,我們需要代數操作I(s) 的表達式,直到它符合圖 2b中變換對表中的一個或許多函數的總和。 如果手工完成,這個過程可能涉及如此繁瑣的代數,以至于它完全否定了在拉普拉斯空間中求解電路而不是求解時域微分方程的好處。
使用 Python 和 SymPy 執行逆拉普拉斯變換
在我們的示例中,我們已經手動完成了所有實際電路工作。 是時候拿出 Python 的計算能力了 SymPy 為我們做逆變換。
首先,我們需要打開一個 Python 環境。 我使用 谷歌合作實驗室為了解決這些問題,因為它是基于Web的,我需要的所有庫都可用,并且它會在命令旁邊呈現任何可視輸出。 該程序類似于 木星筆記本,但它是由谷歌維護的。
第 1 步,我們將導入 SymPy 庫并定義我們的符號 — s 和 t:
from sympy import *
s,t = symbols(‘s,t’)
考慮等式 9,我們可以用符號 ‘s’ 來定義 I(s):
i = 5/(3*(s**2 + 20000*s + 33333333))
最后,我們將I(s)逆變換到時域,并使用以下命令將結果打印到筆記本上:
inverse_laplace_transform(i, s, t).simplify()
然后生成公式 10:
等式10.
請注意,Heaviside 階躍函數在此表達式中表示為 θ(t)。 等式 10 不是我們想要的形式,因為 SymPy試圖保持分數表示而不是四舍五入無理數。 但是,只需在紙上稍作操作,我們可以將 i(t) 重寫為等式 11:
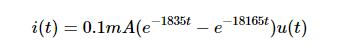
等式 11.
其中 u(t) 表示階躍函數。
完成所有這些操作后,我們就完成了。 使用這個例子,這就是如何在 Python 和 SymPy 庫的幫助下,使用 Laplace空間在二階電路中求解未知的、隨時間變化的量。
Python 還能如何幫助電路分析?
雖然本文的范圍僅限于使用 Python 在分析二階電路時執行逆拉普拉斯變換,但 Python 中的 SymPy庫可用于幫助解決許多類型的電路分析問題。 每當涉及代數時,您都可以使用Python來減輕乏味。 我認為,最好的方法是應用所有必要的電路原理(基爾霍夫定律,歐姆定律等)用手。 然后,當您將問題簡化為紙上的方程或方程組時,使用 Python完成該過程。 拉普拉斯空間中的電路分析是一個充分展示這種方法優勢的舞臺。 通過使用計算機執行逆變換,我們可以大大減少獲得解決方案所需的手動代數操作量,并保留拉普拉斯空間的美麗和好處。
-
電路
+關注
關注
172文章
5852瀏覽量
171942 -
電流
+關注
關注
40文章
6765瀏覽量
131910 -
拉普拉斯
+關注
關注
0文章
35瀏覽量
9645 -
python
+關注
關注
56文章
4783瀏覽量
84473
發布評論請先 登錄
相關推薦
計算機Fortran編程實現偏微分方程拉普拉斯變換
拉普拉斯變換課件教案
什么是拉普拉斯變換
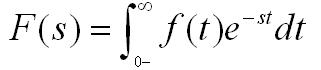
拉普拉斯變換及其逆變換表拉普拉斯變換及其逆變換表





 使用Python分析拉普拉斯空間中的二階電路
使用Python分析拉普拉斯空間中的二階電路
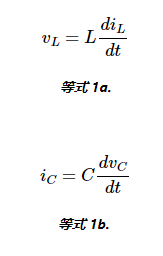










評論