作者:Rob Reeder and Ramya Ramachandran
變壓器用于隔離和將信號從單端轉(zhuǎn)換為差分。在高速A/D轉(zhuǎn)換器的前端電路中使用變壓器時,一個經(jīng)常被忽視的因素是它們從來都不是理想的。對于正弦輸入信號,變壓器引入的任何不平衡都會向ADC的輸入提供不完美的正弦波,并導致整體數(shù)據(jù)轉(zhuǎn)換性能比ADC本來可以提供的性能差。我們在此考慮輸入不平衡對ADC性能的影響,并提供電路示例以實現(xiàn)改進的結(jié)果。
關(guān)于變形金剛
許多制造商提供的型號種類繁多,可能會使變壓器選擇成為一個令人困惑的過程。供應商在具體規(guī)定業(yè)績方面采取的不同方法使挑戰(zhàn)更加復雜。它們在指定參數(shù)的選擇和定義上通常有所不同。
選擇變壓器驅(qū)動特定ADC時需要考慮的一些關(guān)鍵參數(shù)是插入損耗、回波損耗、幅度不平衡和相位不平衡。插入損耗是變壓器帶寬能力的指南。回波損耗也很有用,它允許用戶設計終端以匹配變壓器在特定頻率或頻帶下的響應,這在使用匝數(shù)比大于單位匝數(shù)比的變壓器時尤其重要。本文將重點介紹幅度和相位不平衡,以及它們?nèi)绾斡绊慉DC在高帶寬應用中的性能。
理論分析
即使帶寬額定值很寬,變壓器的單端初級和差分次級之間的耦合雖然是線性的,但也會引入幅度和相位不平衡。當應用于轉(zhuǎn)換器(或其他差分輸入器件)時,這些不平衡會加劇轉(zhuǎn)換(或處理)信號的偶數(shù)階失真。雖然在低頻時通常可以忽略不計,但高速轉(zhuǎn)換器中增加的失真在大約100 MHz時變得非常明顯。我們首先來看看差分輸入信號的幅度和相位不平衡,特別是二次諧波失真,如何影響ADC的性能。
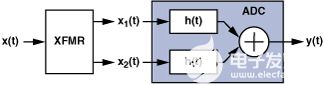
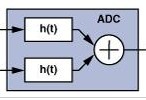
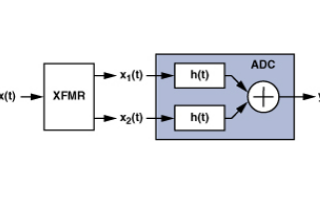
圖1.使用變壓器的ADC前端的簡化框圖。
考慮變壓器的輸入 x(t)。它被轉(zhuǎn)換為一對信號,x1(t) 和 x2(如果 x(t) 為正弦,則差分輸出信號 x1(t) 和 x2(t),的形式為

| (1) |
ADC建模為對稱三階傳遞函數(shù):
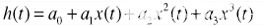 |
(2) |
然后
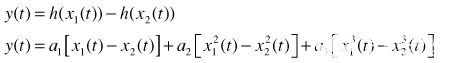
| (3) |
理想情況 - 無不平衡
當 x1(t) 和 x2(t) 是完全平衡的,它們具有相同的星等 (k1 = k2 = k) 并且正好是 180° 異相 (φ = 0°)。因為
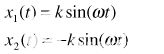 |
(4) |
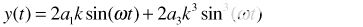 |
(5) |
將三角恒等式應用于冪并收集類似頻率的項,
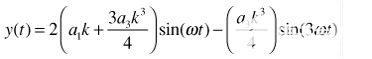
| (6) |
這是差分電路的常見結(jié)果:偶諧波抵消理想信號,而奇次諧波則不會。
量級不平衡
現(xiàn)在假設兩個輸入信號有一個幅度不平衡,但沒有相位不平衡。在這種情況下,k1≠ k2,φ = 0。
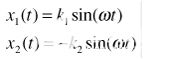 |
(7) |
代入等式3中的等式7,并再次應用三角冪恒等式,
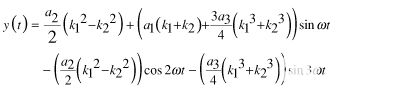
| (8) |
從公式8可以看出,在這種情況下,二次諧波與幅度項的平方差成正比,k1和 k2即。
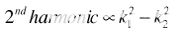 |
(9) |
相位不平衡
現(xiàn)在假設兩個輸入信號之間存在相位不平衡,沒有幅度不平衡。
然后,k1 = k2,φ ≠ 0。
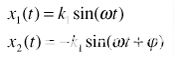 |
(10) |
代入等式3中的等式10并簡化,
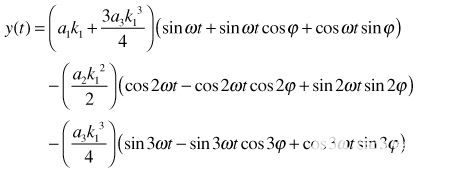
| (11) |
從公式11可以看出,二次諧波幅度與幅度項k的平方成正比。
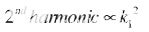 |
(12) |
觀察
比較公式9和公式12表明,二次諧波幅值受相位不平衡的影響比幅度不平衡的影響更嚴重。對于相位不平衡,二次諧波與k的平方成正比1,而對于幅度不平衡,二次諧波與k的平方差成正比1和 k2.由于 k1和 k2大致相等,這個差異很小。
為了測試這些計算的有效性,為上述模型編寫了MATLAB代碼,以量化和說明幅度和相位不平衡對具有變壓器輸入的高性能ADC諧波失真的影響(附錄A)。該模型包括加性白高斯噪聲。
系數(shù),一個我,用于 MATLAB 型號的是一款高性能 16 位、125 MSPS ADC AD9445。AD9445采用圖2所示前端配置,用于生成圖3所示FFT,系數(shù)由此推導。
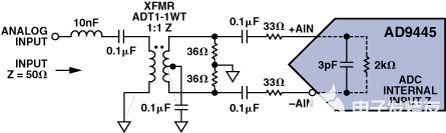
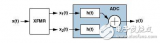
圖2.帶變壓器的AD9445前端配置
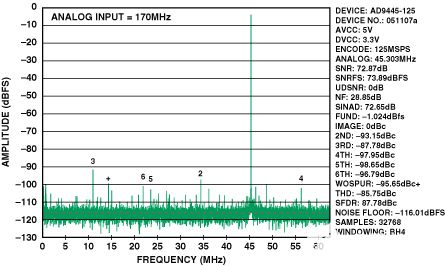
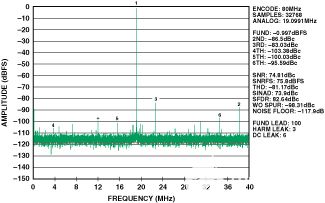
圖3.AD9445的典型FFT,125 MSPS,IF = 170 MHz。
這里的本底噪聲、二次諧波和三次諧波反映了轉(zhuǎn)換器和前端電路的復合性能。轉(zhuǎn)換器失真系數(shù)(a2和3)和噪聲是使用這些測量結(jié)果計算的,并結(jié)合標準1:1阻抗比變壓器指定的170 MHz時0.0607 dB的幅度不平衡和148 MHz時的相位不平衡。
這些系數(shù)在公式8和公式11中用于計算y(t),而幅度和相位不平衡分別在0 V至1 V和0度至50度范圍內(nèi)變化(典型變壓器的不平衡范圍在1 MHz至1000 MHz范圍內(nèi)),并觀察對二次諧波的影響。仿真結(jié)果如圖 4 和圖 5 所示。
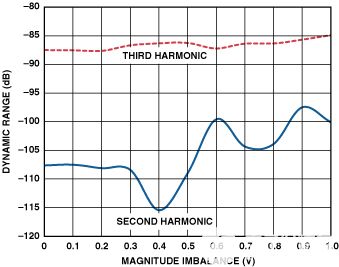
圖4.僅繪制諧波與幅度不平衡的關(guān)系。
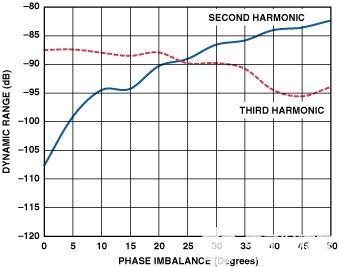
圖5.僅繪制諧波與相位不平衡的關(guān)系圖。
圖4和圖5顯示(a)三次諧波對幅度和相位不平衡相對不敏感,(b)二次諧波在相位不平衡時比在幅度不平衡時惡化得更快。因此,為了從ADC獲得更好的性能,需要具有改善相位不平衡的變壓器配置。圖6和圖7顯示了兩種可行的配置,第一種涉及雙巴倫,第二種涉及雙變壓器。
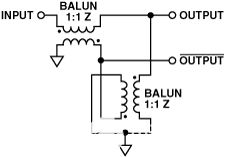
圖6.雙巴倫配置。
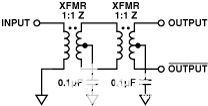
圖7.雙變壓器配置。
在專門設計的表征板上使用矢量網(wǎng)絡分析儀比較了這些配置的不平衡。圖8和圖9比較了這些配置與單個變壓器的幅度和相位不平衡。
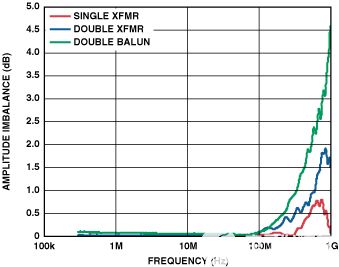
圖8.從 1 MHz 到 1000 MHz 的幅度不平衡。
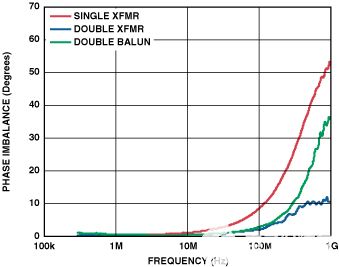
圖9.相位不平衡從1 MHz到1000 MHz。
上圖清楚地表明,雙構(gòu)型具有更好的相位不平衡,但代價是幅度不平衡略有下降。因此,使用上述分析的結(jié)果,似乎可以使用雙變壓器配置來實現(xiàn)更好的性能。使用單變壓器輸入(圖10)和雙巴倫輸入(圖11)的AD9445的FFT圖表明情況確實如此;使用 300MHz IF 信號時,SFDR 提高了 +10 dB。
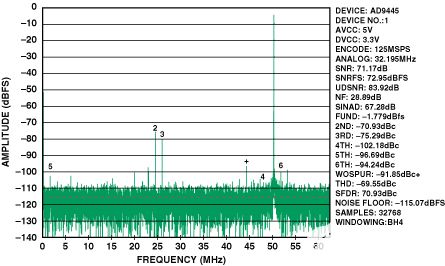
圖 10.單變壓器輸入,AD9445的FFT。125 MSPS,IF = 300 MHz。
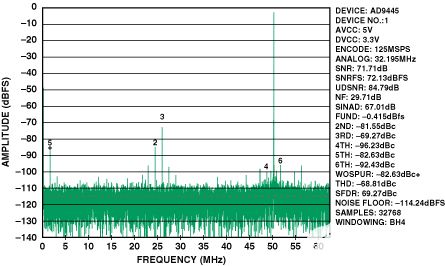
圖 11.雙巴倫輸入,AD9445的FFT。125 MSPS,IF = 300 MHz。
這是否意味著要獲得良好的性能,必須在ADC前端耦合兩個變壓器或兩個巴倫?不一定。分析表明,必須使用相位不平衡很小的變壓器。在以下示例(圖12和圖13)中,使用兩個不同的單變壓器驅(qū)動具有170 MHz IF信號的AD9238。這些示例表明,當ADC由改善高頻相位不平衡的變壓器驅(qū)動時,二次諧波改善了29 dB。
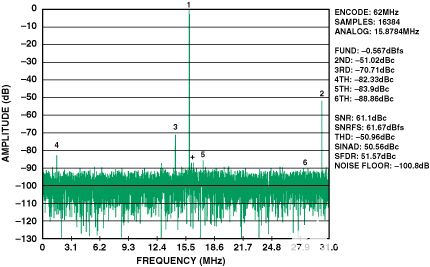
圖 12.單變壓器輸入,AD9238的FFT。62 MSPS,IF = 170 MHz @ –0.5 dBFS,二次諧波 = –51.02 dBc。
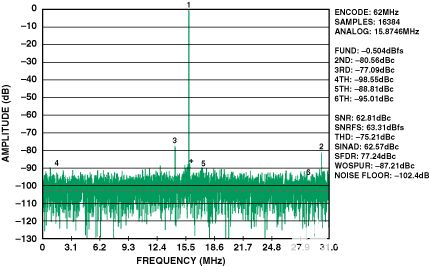
圖 13.單變壓器輸入,AD9238的FFT。62 MSPS,IF = 170 MHz @ –0.5 dBFS,二次諧波 = –80.56 dBc。
結(jié)論
當變壓器用作具有高中頻輸入(>100 MHz)的過程(如A/D轉(zhuǎn)換、D/A轉(zhuǎn)換和放大)的前端時,變壓器的相位不平衡會加劇二次諧波失真。然而,通過使用一對變壓器或巴倫,可以很容易地實現(xiàn)顯著的改進,但代價是額外的變壓器和額外的印刷電路板空間。
如果設計帶寬較小且選擇合適的變壓器,單變壓器設計可以實現(xiàn)足夠的性能。但是,它們確實需要有限的帶寬匹配,并且它們可能很昂貴或物理很大。
無論哪種情況,為任何給定應用選擇最佳變壓器都需要詳細了解變壓器的規(guī)格。相位不平衡對于高中頻輸入(>100 MHz)尤為重要。即使數(shù)據(jù)手冊中未指定,大多數(shù)變壓器制造商也會根據(jù)要求提供相位不平衡信息。網(wǎng)絡分析儀可用于測量變壓器的不平衡作為檢查,或者如果信息不容易獲得。
審核編輯:郭婷
-
轉(zhuǎn)換器
+關(guān)注
關(guān)注
27文章
8639瀏覽量
146895 -
adc
+關(guān)注
關(guān)注
98文章
6452瀏覽量
544148 -
變壓器
+關(guān)注
關(guān)注
0文章
1108瀏覽量
4010
發(fā)布評論請先 登錄
相關(guān)推薦
諧振轉(zhuǎn)換器同步整流器的設計注意事項
高頻諧振轉(zhuǎn)換器設計注意事項②
高頻諧振轉(zhuǎn)換器設計注意事項,第2部分
使用雙變壓器配置時寬帶ADC前端設計考慮
農(nóng)村配電變壓器維護注意事項
當使用雙變壓器配置時寬帶ADC前端設計考慮
變壓器預防性試驗注意事項及預防性試驗標準

主要內(nèi)部廣告:指定A/D轉(zhuǎn)換器:中頻采樣應用的注意事項

應用工程師咨詢:寬帶A/D轉(zhuǎn)換器前端設計注意事項II
高頻開關(guān)電源變壓器的設計及注意事項





 寬帶A/D轉(zhuǎn)換器前端設計注意事項:何時使用雙變壓器配置
寬帶A/D轉(zhuǎn)換器前端設計注意事項:何時使用雙變壓器配置










評論