作者 |馮勁草上海控安可信軟件創新研究院研究員
版塊 |鑒源論壇 · 觀模
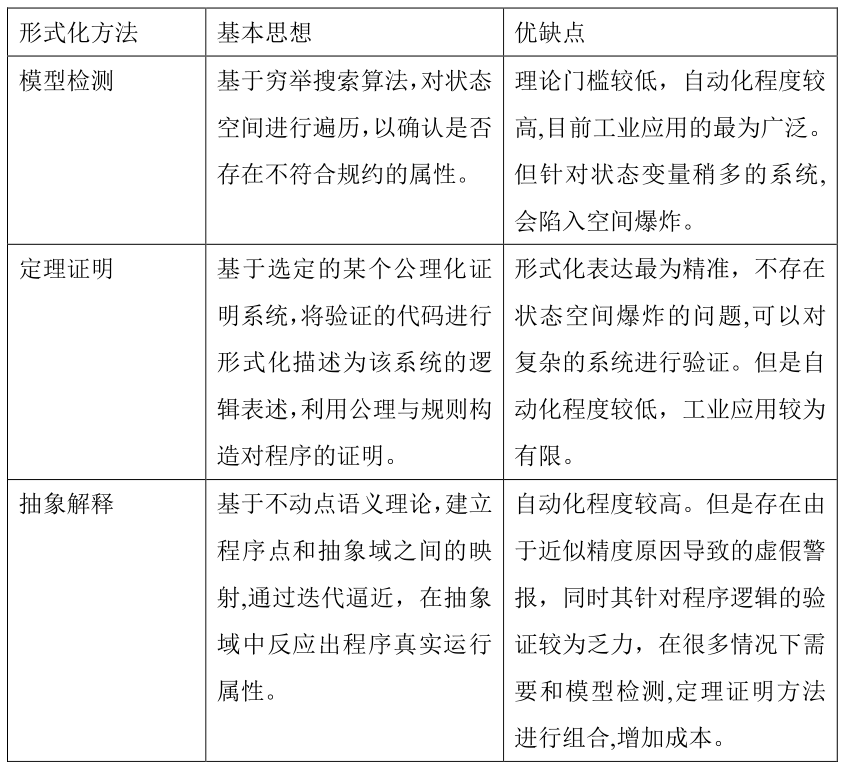
01形式化方法基本概念
形式化方法是基于嚴格的數學基礎,通過采用數學邏輯證明來對計算機軟硬件系統進行建模、規約、分析、推理和驗證,是用于保證計算機軟硬件系統正確性以及安全性的一種重要方法。
形式化方法使用數學及邏輯證明的手段對計算機系統進行建模、規約、分析、推理,其主要涵蓋以下幾個研究方向:定理證明、形式模型、形式語義與形式建模、形式規約、形式驗證技術。下面以高可信工業領域實際應用中最廣泛的形式化規格說明、定理證明和模型檢測為例,介紹其基本原理。
02形式化規格說明
通過對編程語言的語義進行嚴格的定義,加之使用形式模型對計算機系統的行為進行建模,最終形成形式化規格說明書來對計算機系統的行為進行推理驗證,形式規格說明是對計算機系統進行驗證的基礎,形式規格說明的基礎是形式語義學和形式建模。
形式語義學(formal semantic)是研究程序設計語言的語義的學科,以數學為工具,利用符號和公式,精確地定義和嚴格地解釋計算機程序設計語言的語義,從而消除設計者、開發者和使用者之間的理解的差異性。形式語義幫助理解語言,指導語言的設計,幫助編寫編譯器和語言系統,支持程序驗證和軟件可靠性,有助于軟件規范化。形式語義學主要分為四大流派:操作語義,代數語義,指稱語義和公理語義。操作語義著重模擬數據處理過程中程序的操作;代數語義基于代數,用代數結構刻畫程序語法實體,用代數公理刻畫實體含義以及語法實體間的關系;指稱語義主要刻畫數據處理的結果,而不是處理的細節;公理語義用公理化的方式描述程序對數據的處理,主要用于程序的推理和論證。早期的程序語言的語義只是在論文中給出,不能用計算機測試語義的正確性和一致性,也不能用于程序的驗證和分析。中期的語義一般用定理證明器的元語言實現,此類語義可用于程序語言語義和程序性質的手動或半自動驗證。K框架是最近流行的定義語言的形式語義的途徑,基于重寫邏輯,通過定義語言的操作語義,自動生成對應程序的形式分析和驗證工具。
形式建模是對計算機軟硬件系統的行為和性質用某種形式模型精確的刻畫。形式模型一般采用通用形式建模語言(如Petri Net、Event-B、Pi-演算、CSP、SysML、Lusture等)或者專用形式模型(如有限自動機、下推自動機、概率自動機等)來進行。函數式程序可以用樹自動機、高階下推自動機來建模,自適應系統與多智能體一般使用Petri網、UML、Z以及馬爾可夫模型等來建模,對于深度神經網絡的形式建模最近也成為研究熱點。
2.1 形式化規格說明舉例
假設有一個“農夫過河”系統,其需求文檔如下:
(1)一個人帶著狼、山羊和白菜在一條河的左岸,有一條船,大小正好能裝下這個人和其它三者之一,人和他的隨行物都要帶過岸,但他每次只能帶一樣東西擺渡過河。
(2)如人將狼和羊留在同一岸,無人照顧,那么狼會把羊吃掉。同樣,如羊和白菜在同一岸,無人照顧,那么羊會吃了白菜。
該系統在設計完成后,應當滿足性質:至少存在一條過河路徑,使得人和他的隨行物全部渡過了河。
為了驗證上述系統是否滿足相對應的性質,使用NuSMV形式化驗證工具進行性質的驗證工作。NuSMV是一款經典的基于BDDs(Binary Decision Diagrams)的模型驗證器。在本例中,我們將使用NuSMV提供的形式化描述語言對一個系統的需求進行形式化規格說明的轉化。
用對上述自然語言描述的需求文檔進行形式化建模,使用NuSMV的形式化語言描述如圖1所示。

圖1 農夫過河系統的形式化規格說明
對待驗證的性質使用性質描述語言進行描述,如圖2所示。

圖2 待驗證性質的形式化描述
使用NuSMV進行模型檢測的基本原理是將形式化語言描述的系統和待驗證的性質抽取形成一個狀態遷移系統,在該狀態遷移系統中若存在一個可接收狀態即為該系統滿足特定性質。后續的形式化驗證工作即是建立在該形式化規格說明上的。
03形式化驗證技術
3.1 定理證明技術
在形式語義與形式建模以及形式規約的基礎上,將計算機系統的分析與驗證問題轉化為邏輯推理問題或者形式模型的判斷問題,用定理證明工具/求解器或者某個形式模型的原型工具來進行驗證。形式化驗證主要的技術有定理證明和模型檢測。
定理證明的基本思想是,將程序滿足其形式規約的證明問題轉化為一組數學命題的證明。若這一組數學命題,稱作證明義務(proof obligation),能夠蘊含“程序滿足其規約”這一命題,那么我們可以說該證明系統是正確(sound)的。
3.1.1簡單推理舉例
在數學運算中,有許多運算公理及其推導出的運算屬性。在給出如圖3所示的運算公理時,證明運算屬性P1:x=x+y*0 成立便是一個簡單的推理證明過程。推理證明過程如圖4所示。
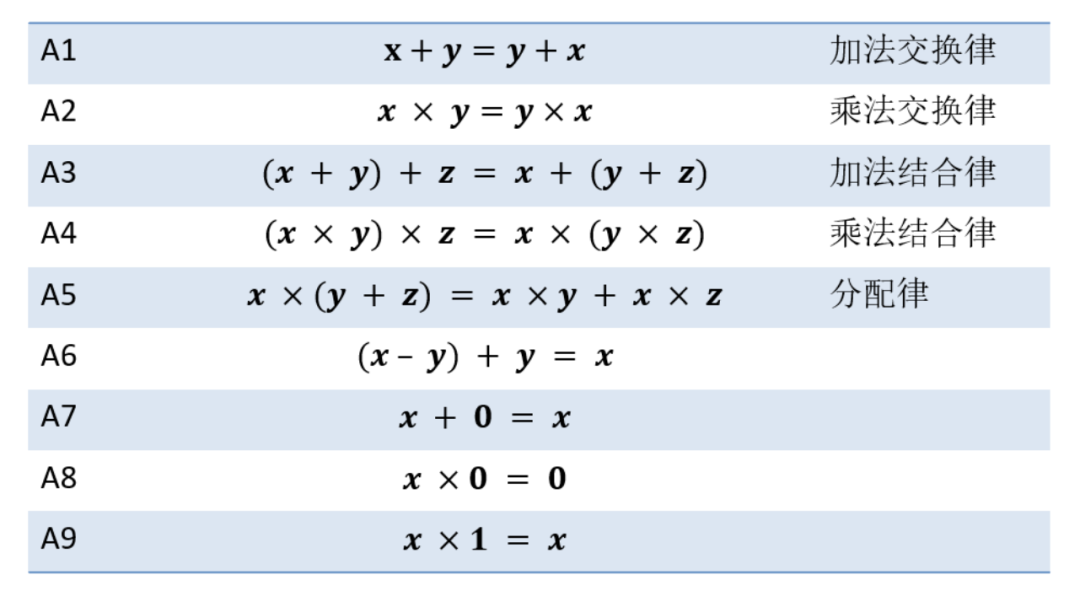
圖3數學運算公理

圖4 數學運算屬性證明過程
3.1.2定理證明舉例
同上述章節中推導出來的數學運算的性質等同,在程序中,使用Hoare logic來證明程序的部分正確性。它以一階邏輯為基礎,利用運算規則、公理與推理規則進行程序證明。即:如果斷言P在程序S執行前為真時可推出斷言R在S終止時為真,則程序S對于P和R來說是正確的,使用三元組表示為:{P} S {R}。
嘗試證明:{x <> y∧x > y} x := y – 1 {x = y ∨ x < y}的正確性。在該語句中,P={x<>y ∧x > y} ;S=x:=y-1;Q={x = y ∨ x < y}。為了證明該語句,需要使用兩條公理,一條是賦值公理(Ass-D0),一條是推論規則。賦值公理指,{P[f/x]} x := f {P}成立,P[f/x]是用f替代P中所有x得到的謂詞表達式。推論規則指:如果{P} S {R}成立,則對于所有Q=>P,{Q} S {R}均成立。根據上述兩條公理,當我們想證一條{P}S{R}成立時,我們可以根據賦值公理找到一個一定使后置條件滿足的情況{R[f/x]}x:=f{R},當P能夠=>P[f/x]時,{P}S{R}得證。如圖5所示,使用賦值公理,將后置條件中的x使用賦值語句中的x=y-1替代,得到{y y∧x >y}=>{y y∧x > y} x := y – 1 {x = y ∨ x < y}成立。由于y < y + 1 <=> true,所以{ x <> y∧x >y}=>{y y∧x > y} x := y – 1 {x = y ∨ x < y}成立。
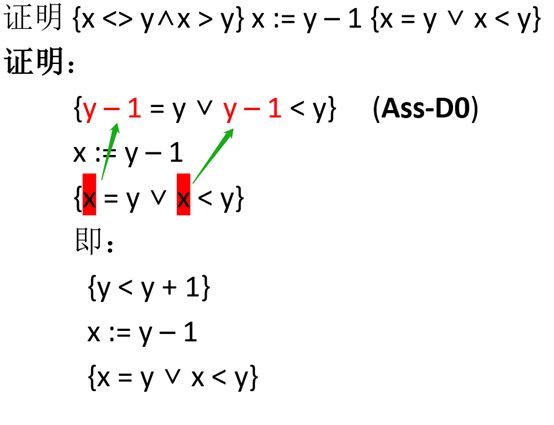
圖5 賦值公理的使用過程
3.2模型檢測技術
模型檢驗的基本思想是通過遍歷系統的狀態空間以驗證系統模型是否滿足給定的關鍵性質,并在不滿足性質時給出具體反例路徑。因此,如何對模型狀態空間進行快速遍歷對于模型檢驗至關重要,而狀態空間爆炸問題則自然成為模型檢驗技術面臨的主要問題。與模型檢驗技術取得成功的硬件領域相對比,軟件系統的狀態空間復雜性更高。將相關狀態空間符號化表達, 并在符號化后的空間上進行計算和遍歷是軟件模型檢驗的基本方法。然而,即使是符號化后的狀態空間,其驗證也并不是一個簡單問題,因此對復雜的狀態空間進行抽象簡化是一個重要研究方向。
3.2.1 模型檢測舉例
將上述章節中的農夫過河系統轉化成相應的狀態遷移圖如圖6所示,其中MGCW-Empty表示初始狀態,“-”左邊的符號表示對應的符號在左岸。“-”右邊的服務表述對應的符號在右岸。M表示人,G表示羊,C表示白菜,W表示狼,箭頭表示表示每次在船上運輸的物品的種類。其中因為有一些約束限制所以導致一些理論上會出現的狀態并沒有出現。
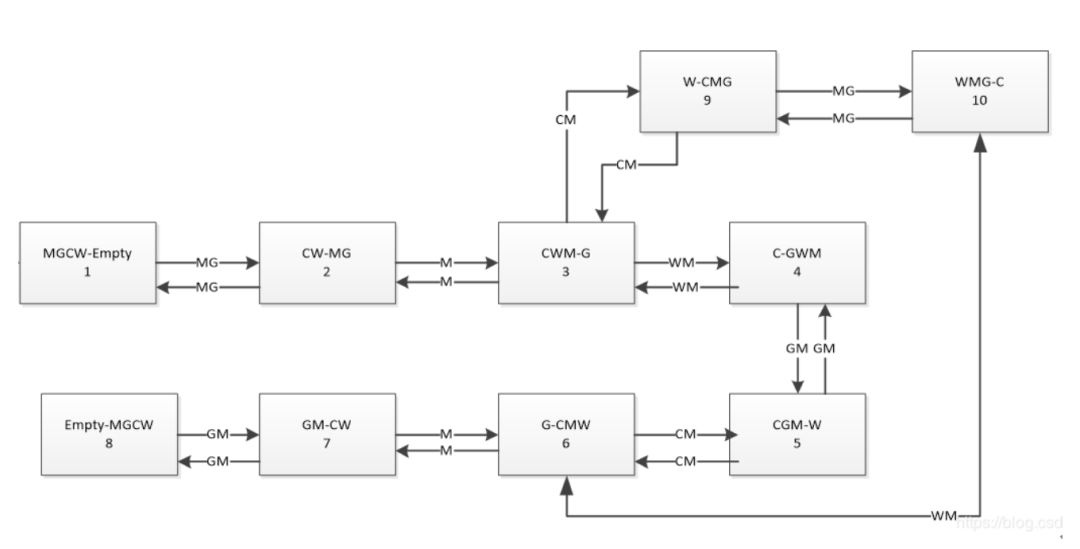
圖6 農夫過河狀態遷移圖
該系統待驗證的性質在該圖中可表述為初始狀態為“MGCW-Empty”的情況下, 是否存在一條路徑,能夠到達終止狀態“Empty-MGCW”。即在圖6中,是否存在一條路徑,使得狀態1能夠到達狀態8。若存在該路徑,那么說明經過驗證,該系統滿足了該性質,若不存在該路徑,那么說明經過驗證,該系統不滿足該性質。
關于形式化驗證的定理證明、模型檢測等方法在行業中的實際應用情況,我們將在后續的章節中陸續為大家介紹。
主要參考文獻:
1. Jifeng He: A New Roadmap for Linking Theories of Programming. UTP 2016: 26-43.
2. CCF Formal Methods Technical Committee. Advances and trends on formal methods. In: The Progress Report of Computer Science and Technology in China from 2017 to 2018. Beijing: China Machine Press, 2018. 1-68(in Chinese with English abstract).
3. Ro?u G, ?erb?nut? T F. An overview of the K semantic framework[J]. The Journal of Logic and Algebraic Programming, 2010, 79(6): 397-434.
4. Cimatti A , Clarke E , Giunchiglia F . NUSMV: a new symbolic model checker[J]. International Journal on Software Tools for Technology Transfer, 2000, 2(4):410-425.
5. Wang S, Zhan N, Zou L. An improved HHL prover: an interactive theorem prover for hybrid systems[C]//International Conference on Formal Engineering Methods. Springer, Cham, 2015: 382-399.
6. Cousot P, Cousot R. Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints[C]//Proceedings of the 4th ACM SIGACT-SIGPLAN symposium on Principles of programming languages. 1977: 238-252.
審核編輯黃宇
-
計算機
+關注
關注
19文章
7430瀏覽量
87735 -
建模
+關注
關注
1文章
300瀏覽量
60741 -
形式化
+關注
關注
0文章
4瀏覽量
711
發布評論請先 登錄
相關推薦
CT的基本原理及方法
無線充電的基本原理是什么
形式化方法和測試技術及其在安全中的應用
Web服務系統的形式化的語義模型
軟件形式化開發的水波優化方法
基于幾何代數的高階邏輯形式化建模
形式化方法背后的動因和關鍵技術及行業應用




 形式化方法基本原理初探
形式化方法基本原理初探










評論