本文摘要
眾所周知,(串行) 程序驗證的復雜度極高。并發程序在大大提高軟件執行效率的同時,也會顯著增加程序執行的不確定性,使得并發程序驗證的復雜度更高。有趣的是,并發程序中內存訪問的執行順序可以利用偏序關系進行建模。沿著這個思路,我們在基于 SMT 的并發程序驗證方面做了一些探索,提出了一個專用于并發程序驗證的 SMT 理論,設計了相應的判定算法。基于上述理論開發的并發程序驗證工具 Deagle 獲得 SV-COMP 2022 并發安全賽道冠軍。
以下為正文。
# 背景 #
本質上講,要驗證一個程序的正確性,需要驗證程序中所有執行都正確。對并發程序來說,由于線程之間的交織,不同線程中程序指令的執行順序有很多種情況,導致并發程序的執行空間遠大于同等規模下串行程序的執行空間。因此,并發程序驗證的復雜度遠高于串行程序。
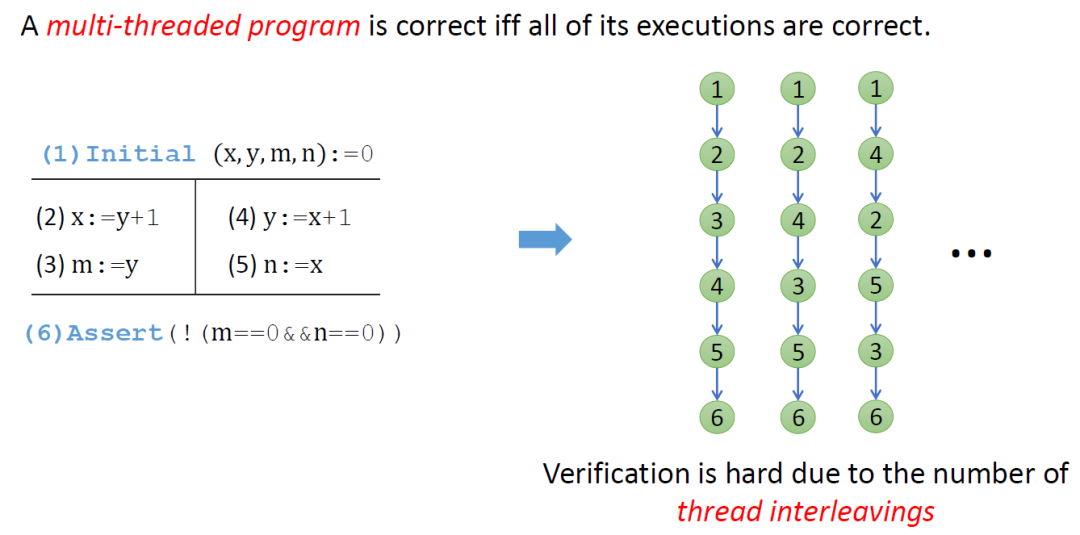
目前存在許多致力于緩解執行空間爆炸的并發程序驗證技術,包括偏序規約 (Partial Order Reduction)、限定上下文切換次數 (Context Bounded)、惰性順序化 (Lazy Sequentialization) 等。這些技術雖然在某種程度上可以有效降低需要考慮的程序執行的絕對數量。但從本質上來講,仍然需要 (顯式地) 遍歷程序中的所有執行,驗證規模仍然非常有限。
那么有沒有可能像串行程序一樣,將并發程序驗證問題編碼成 SMT 公式,再借助于 SMT Solver 進行求解?采用這種方案的好處是:編碼成 SMT 公式后,程序的執行空間可以通過 SMT 公式的解空間來表達,由此可以借助 SMT 求解器,通過搜索 SMT 公式的解空間來隱式地遍歷程序的執行空間。
# 一個簡單的示例 #
并發程序編碼的核心問題是確定不同線程之間程序指令的執行順序。下面通過一個例子來展示如何將一個并發程序編碼成 SMT 公式,后面再介紹怎么對編碼得到的 SMT 公式進行更有效的求解。
下圖左邊展示了一個非常簡單的并發程序,包含一個主線程和兩個子線程。我們首先將其轉換為 SSA (Static Single Assignment) 形式。注意這里的 SSA 與串行程序 SSA 的不同:串行程序 SSA 對每一次寫操作引入變量的一個新拷貝,而并發程序 SSA 對于每一次讀操作也需要引入變量的一個新拷貝。

Concurrent Static Single Assignment-1
得到并發程序的 SSA 的形式之后,就可以對其進行編碼了。注意本例程是一個非常簡單的不含分支的程序 (分支程序的編碼后面再討論)。不含分支的程序都可以轉化為只含賦值語句和斷言語句的程序。
如下圖所示,每條賦值語句和斷言語句都可以直接編碼成邏輯公式,其中編碼斷言語句時需要對斷言條件取反,稱為錯誤條件 (Error condition)。

Concurrent Static Single Assignment-2

# 內存模型 #
為了刻畫并發程序變量之間的讀寫關系,必須考慮 內存模型。
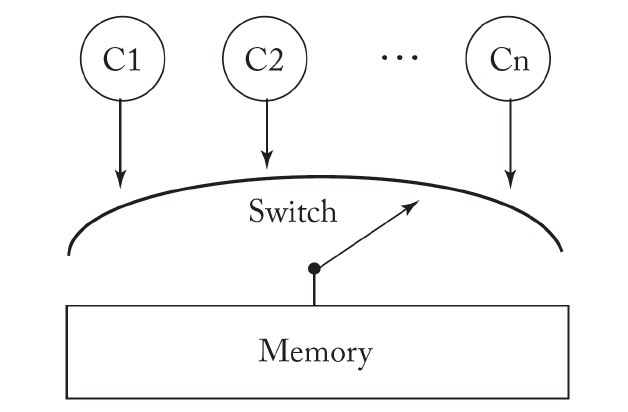
Memory Model
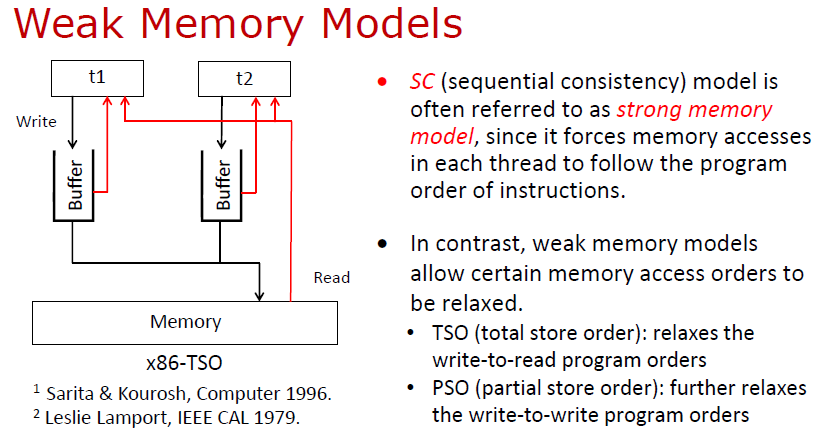
最簡單的一種內存模型叫順序一致性模型 (Sequential Consistency, SC)。在內存模型中,每個線程按照自己的指令序列發送訪存指令到內存系統;如果最后訪存指令被內存系統執行的順序跟線程發送的順序是一致的,就稱為順序一致性模型。很多情況下,順序一致性模型也稱強內存模型 (Strong Memory Model)。
與強內存模型對應,還有另一種內存模型,稱弱內存模型 (Weak Memory Model, WMM)。內存模型與底層的硬件實現密切相關。硬件領域的許多優化機制在提高硬件處理速度的同時,也導致順序一致性的假設不再成立。
為此,需要引入更弱假設的內存模型,即弱內存模型。常見的弱內存模型包括 TSO (Total store ordering)、PSO (Partial store ordering) 等。
為方便理解,下面的討論主要聚焦于 順序一致性模型。對于弱內存模型,我們將在最后進行單獨討論。
# 符號化編碼 #
在對并發程序進行編碼時,除了要考慮賦值,還必須考慮所有訪存操作的執行順序,為此引入 事件 的概念。每個事件代表一次訪存操作。后面我們將基于事件來定義執行順序。
設為一個變量,以 表示對應這個變量的訪存事件。在本例中,對變量 有四次訪存 (讀或者寫) 事件。我們約定以上標 w 表示寫事件,如 ;以上標 r 表示讀事件,如 。
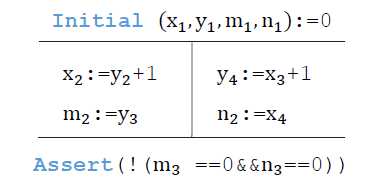
下面我們基于偏序關系(Partial orders) 來定義訪存操作事件之間的先后順序。
# 符號事件圖
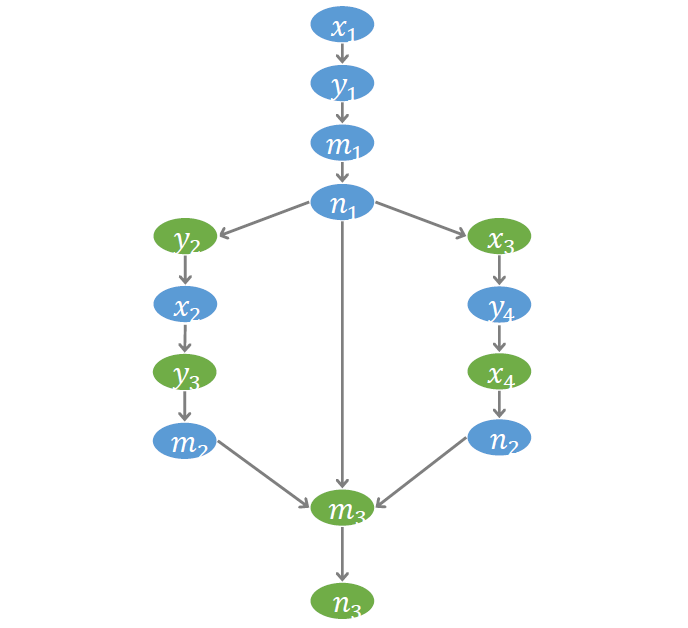
為了更好的刻畫訪存操作之間的偏序關系,我們建立了一個稱為符號事件圖 (Symbolic event graph) 的結構。圖中每個節點代表一個事件,每條邊代表一個偏序。如下圖, 到 有邊,表示事件 發生在事件 之前。我們約定以藍色節點代表寫事件,綠色節點代表讀事件。符號事件圖對后面的驗證算法非常重要。驗證過程的許多推理都將在這個圖上進行。
# PO 序
第一個需要刻畫的偏序關系,叫做 Program Order (PO),即訪存操作被線程發出的順序。對于順序一致性模型,PO 序是程序執行必須遵循的一個順序。但對于弱內存模型,在最后實際執行的順序中,PO 序可能會被打破。
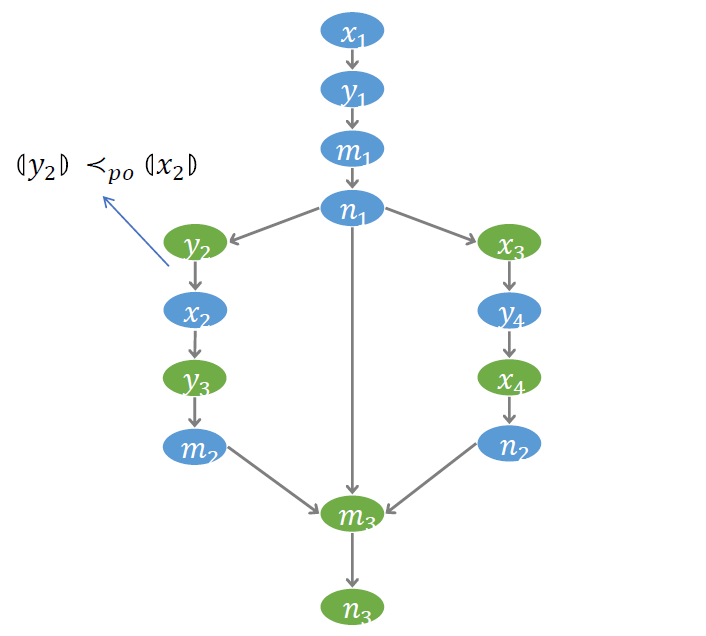
# RF 序
第二個需要刻畫的偏序關系,叫做 Read-from (RF),刻畫了讀操作讀到的值與寫操作寫入的值之間的關系。
如示例程序中的 ,其讀到的值可能來自于 ,也可能來自于 。為此我們引入兩個布爾變量 和 。
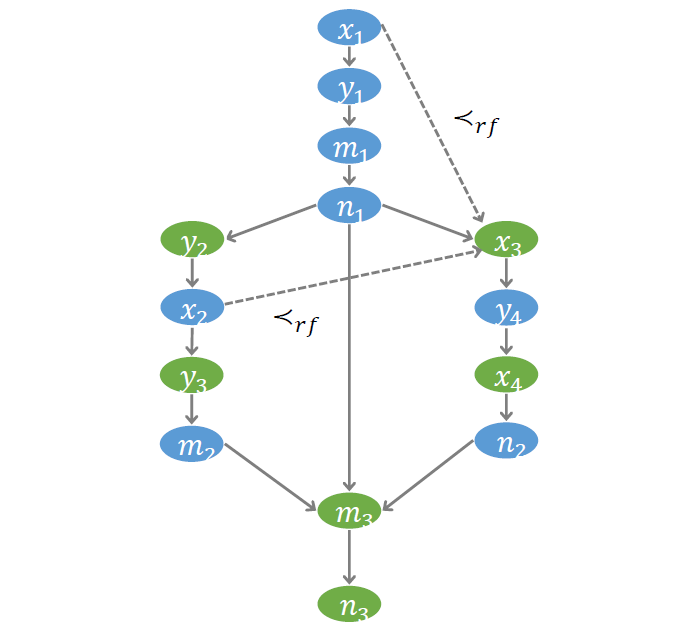
如下所示, 為真,表示 讀到的值來自于 ;此時 對應的寫操作必定發生在 對應的讀操作之前,即 ,稱為 RF-Ord 約束;
同時,在這種情況下, 變量的值一定等于 變量的值,即 ,稱為 RF-Val 約束。
類似地,對應于 為真,我們也可以推導出類似的結論。
此外,由于 的值要么來自于 ,要么來自于 ,所以 和 必有一個為真,即 ,稱為 RF–Some 約束。
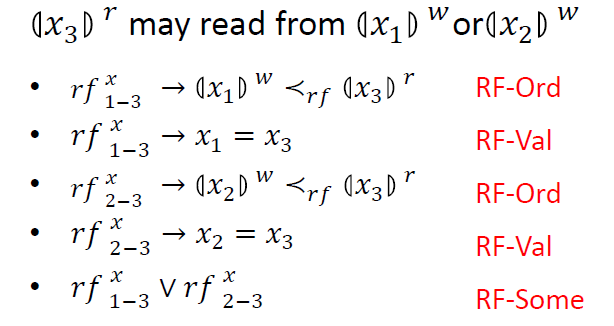
通過上述三種約束,就將變量之間的 Read-from 關系刻畫出來了。
# WS 序
第三個需要刻畫的偏序關系,叫做 Write-serialization (WS)。對于一個讀操作,如果前面有對相同變量的多次寫操作,則讀到的值一定是最后一次寫操作所寫入的值。因此,對于同一個內存地址的多次寫操作,必須考慮它們之間的執行順序,稱 WS 序。
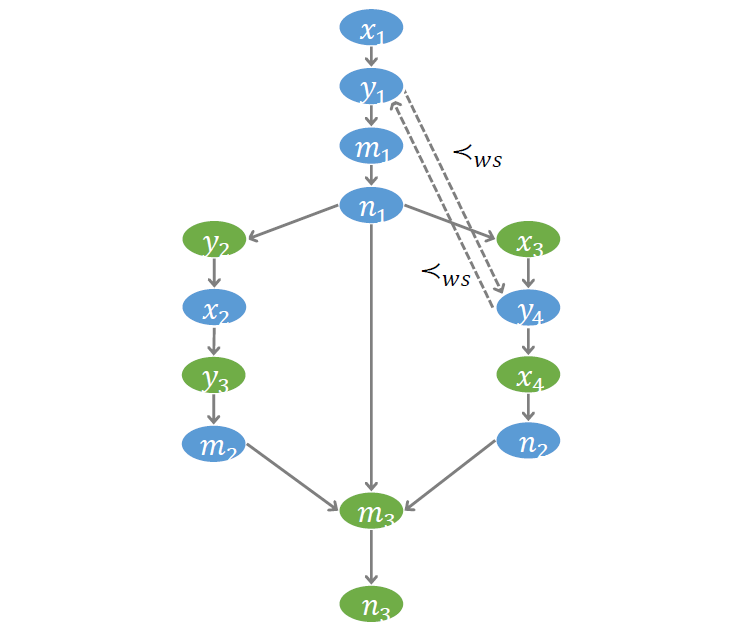
為了編碼 WS 序,引入 WS 變量。每個 WS 變量都是一個布爾變量。例如,示例程序中的 、 都是對 的寫操作。以 表示 在前, 在后的情況。

注意編碼過程中需要引入大量 WS 變量。理論上講,對相同地址的每一對寫操作,都需要引入兩個 WS 變量。
# FR 序
第四個需要刻畫的偏序關系,叫 From-read (FR)。
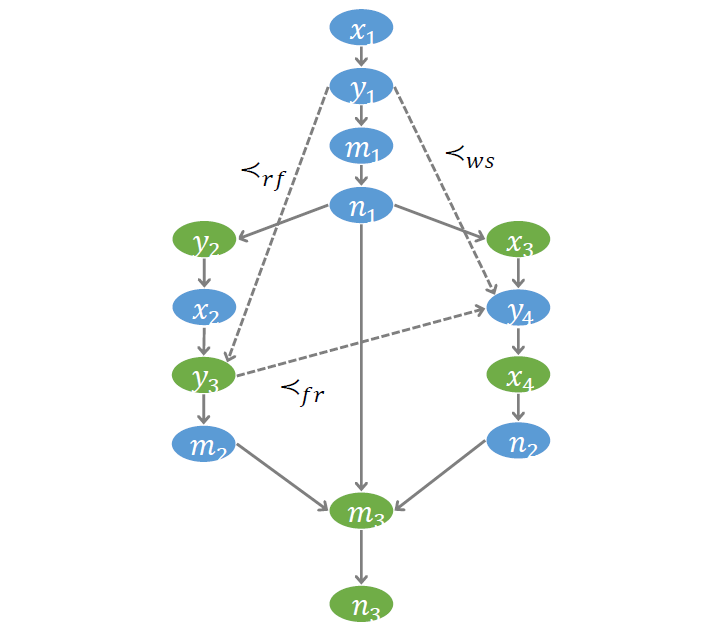
考慮示例程序, 是對變量 的讀, 和 是對變量 的寫;假設已知 讀到的值來自 的寫,并且 發生在 之前,則 一定也發生在 之前;否則 就成為距離 最近的寫操作, 讀到的值則應該來自于 而非 。即,
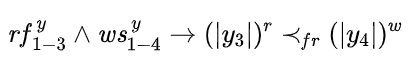
稱該約束為 FR 約束。
在編碼中需要引入大量 FR 約束。理論上,對每一對 WS 和 RF 變量,都需要引入一個 FR 約束。
# 驗證條件
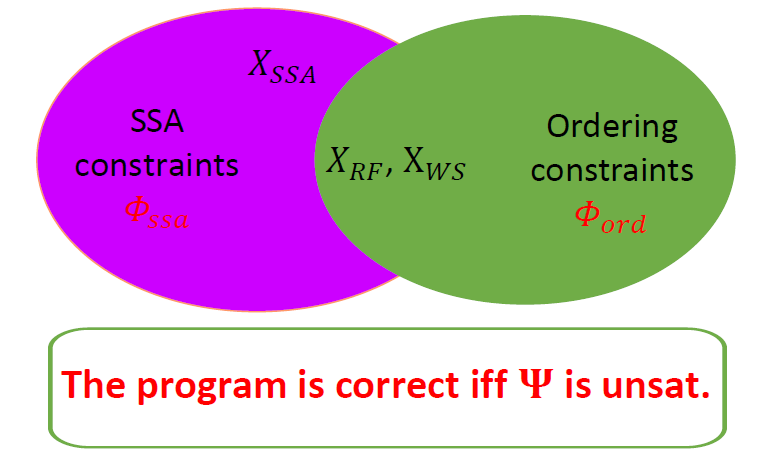
將前面所有約束 (包括針對賦值語句和斷言語句引入的約束,以及針對執行順序引入的約束) 進行合取,就得到了并發程序的驗證條件 (Verification Condition)。該驗證條件是一個 SMT 公式,后面的驗證就可以交給 SMT Solver 進行求解了。我們可以證明:并發程序滿足給定斷言屬性當且僅當其驗證條件不可滿足。

# SMT 理論 #
進一步分析上面的驗證條件公式可以發現,整個公式分為 和 兩部分,其中 只涉及布爾變量和偏序關系,而 中不涉及任何偏序關系。顯然 可以直接采用現有的 SMT Solver 求解;而對于 ,目前缺乏直接對其求解的 SMT Solver。
在已有的基于 SMT 的并發程序驗證方法中 (這些方法在符號化編碼方面與我們的方法有一些差異,但基本上也可以分為 和 兩部分),大多借用已有的 SMT 理論來間接地解決 。它們為了比較程序中訪存操作的先后順序,會引入時鐘的概念,即給每次訪存操作打上一個時間戳,然后通過比較時鐘戳的值來確定事件的先后順序。在這些方法中,時鐘戳一般被定義成整型變量,因此時間戳的比較可以通過已有的整型差分邏輯 (Integer difference logic) 來定義。
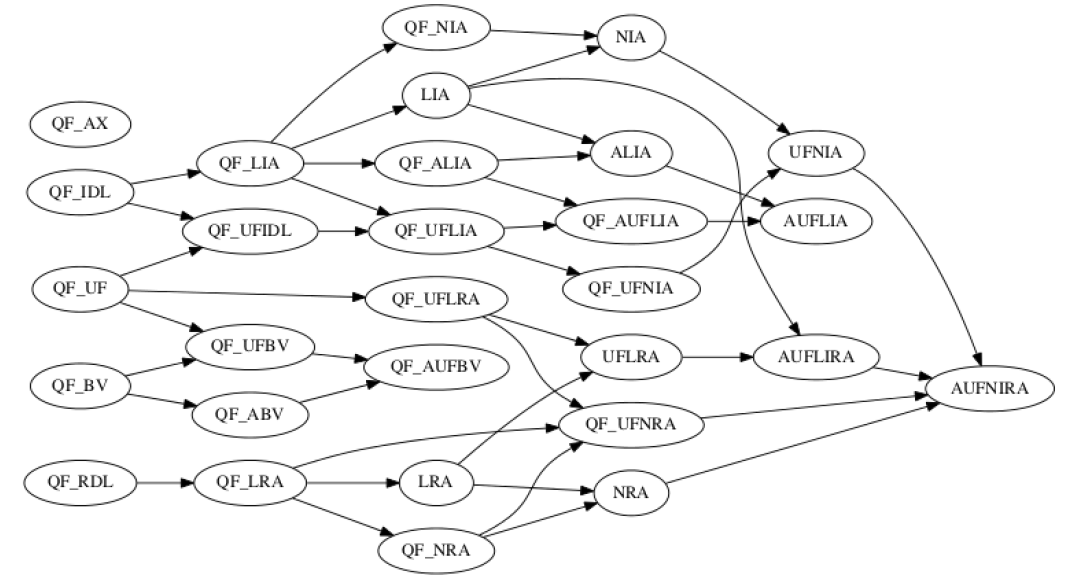
已有方案的缺點主要體現在以下兩方面:
在這種方案下,為了比較事件的先后順序,需要計算每個時間戳的確切值。事實上我們對于這些確切值并不關心。例如,考慮事件 和 ,設 和 是它們的時間戳,為了證明 發生在 之前,我們只需要證明 ,而無需計算出類似 的確切值。
更重要的是,在該方案下,為保證符號化公式編碼了程序的所有執行,必須在編碼階段窮舉上面介紹的所有約束。窮舉編碼需要引入大量變量,刻畫大量 FR 和 WS 約束,這會給后端的 SMT Solver 帶來嚴重負擔,導致嚴重的效率問題。
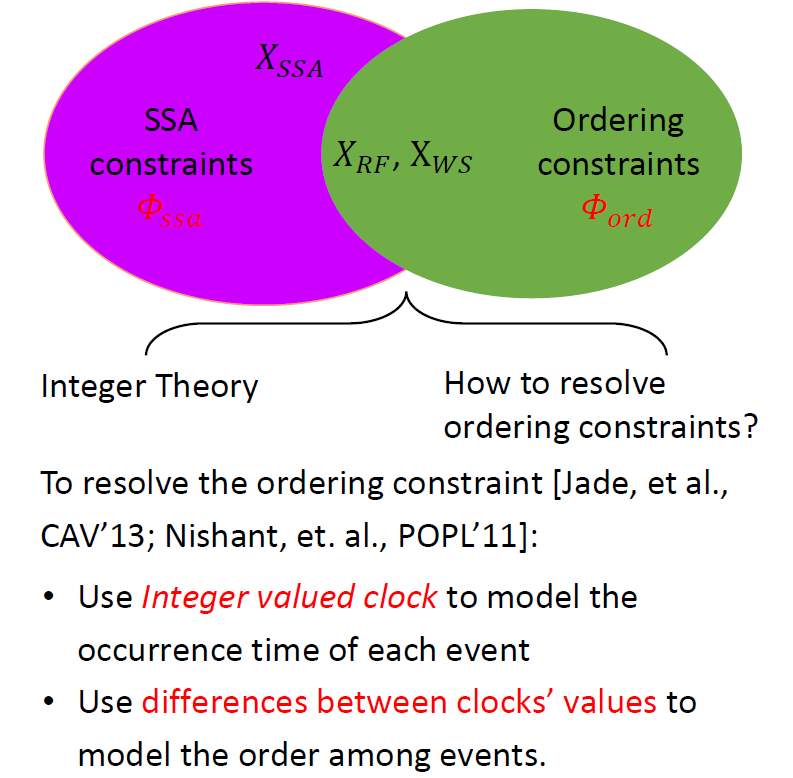
我們的主要想法是定制一個專屬的 SMT 理論,稱 序關系一致性理論 (注意這里的理論是一階理論的概念),用于描述和刻畫 約束。我們這個新的 SMT 理論完全基于序關系來定義,不需要對事件發生的確切時間進行刻畫。其次,我們還希望開發一個專用于 的判定過程,實現對 約束的更有效求解。
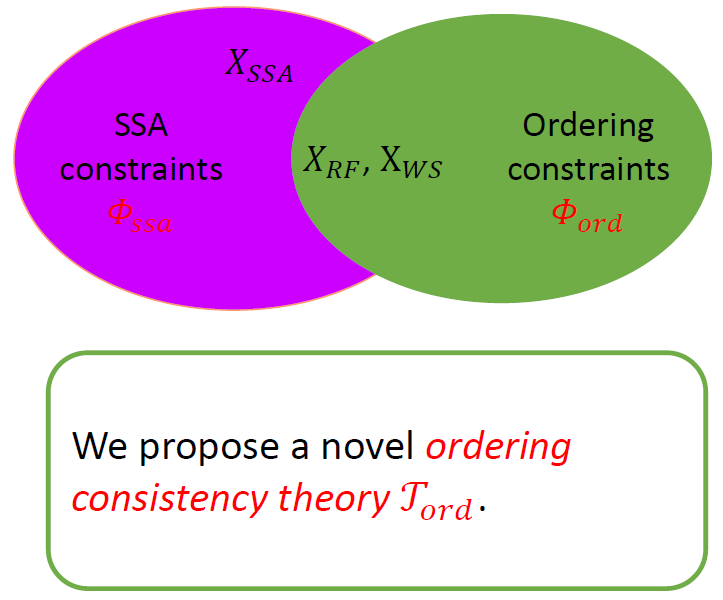
# 理論定義
在我們的 序關系一致性理論 [1]中,分別以 表示 PO、RF、WS、FR 偏序關系, 表示訪問事件。

主要包含下列三個公理:
第一個公理規定了 所代表的 偏序關系,以及這些偏序關系中對事件訪存類型 (讀還是寫) 的要求。比如 RF 關系 要求 為寫, 為讀。

第二個公理規定了 FR 推理規則,即對于任意兩個寫操作 和一個讀操作 ,如果已知 的值讀自 (即 ),并且 先于 發生 (即 ),則 也必定先于 發生 (即 )。
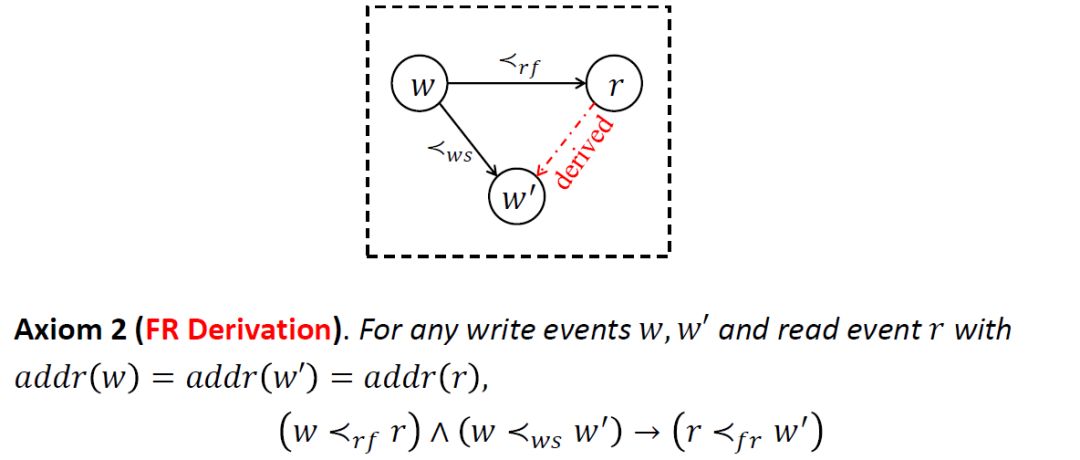
在 的判定過程中,我們會依據 FR 公理反復應用該推理規則,直至推導出所有可能的 FR 偏序關系。FR 公理的本質是將 FR 推導挪到 SMT 后端進行,這樣在編碼階段就沒有必要再去窮舉所有可能的 FR 約束了。依據 FR 公理的推導是按需進行的,即只有在兩個前提都滿足的情況下才會推導結論中的 FR 關系。這種按需推理顯然比窮舉所有可能的 FR 約束更加有效。

第三個公理刻畫的是 多種偏序關系之間的一致性。前面引入的 等偏序關系都是 happens-before 關系的特例。顯然,所有 happens-before 關系的并集中不應該出現環,否則就會出現某個事件發生在自身之前的悖論。我們的判定過程正是依據這個公理來判定 公式的可滿足性。
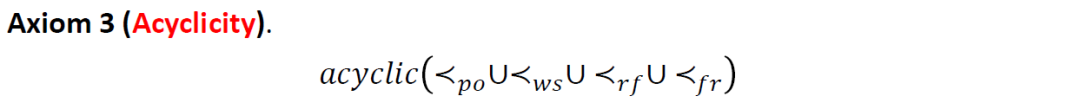
如下 Lemma 將程序正確性與 公式的一致性聯系起來。給定程序的一條執行,如果它的訪存操作的偏序關系滿足一致性公理,就稱該執行是一致的 (Consistent),否則就稱它是不一致的 (Inconsistent)。不一致的執行在真實的程序運行中不可能出現。

給定程序的一條執行,如果它滿足待驗證屬性,就稱它是正確的 (Correct),否則就稱它是不正確的 (Incorrect)。任何一條錯誤且一致的執行稱為程序相對于待驗證屬性的反例。程序滿足待驗證屬性,當且僅當程序中不存在任何一條反例。
# 判定過程 #
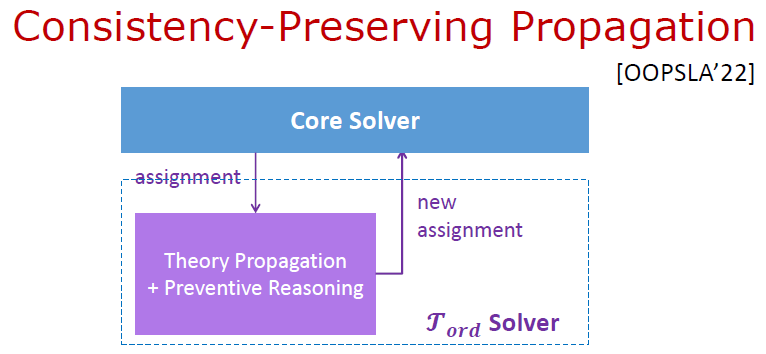
一個 SMT Solver 通常由一個 Core Solver 和若干個 Theory Solver 構成。每個 Theory Solver 實現一個 SMT 理論的判定過程,Core Solver 則負責 Theory Solver 之間的協調。下圖即我們為 定義的求解器。
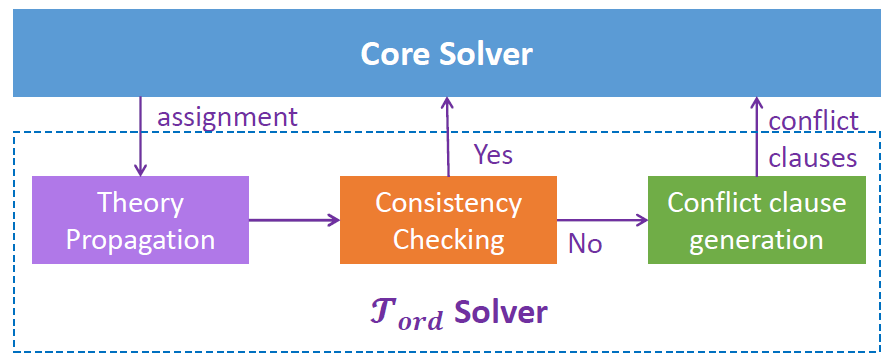
對應程序驗證條件的 SMT 公式通常涉及很多 SMT 理論。給定一個 SMT 公式,SMT Solver 先進行初始化工作,將公式分解為 (可滿足性等價的) 若干個完全屬于某 SMT 理論的子公式。每個子公式再交給對應的 Theory Solver 進行求解。不同 Theory Solver 之間的信息交互由 Core Solver 負責。
下面只討論針對 公式的判定過程。
第一步是 理論傳播 (Theory Propagation),即基于當前已知的偏序關系,盡量地去做 FR 推導。
第二步是 一致性檢查 (Consistency Checking)。在理論傳播的過程中會產生許多 FR 關系,所有這些關系都會被加入到符號事件圖中,然后需要判斷在當前符號事件圖中是否存在環 (依據一致性公理)。
在一致性檢查中,我們引入了一個 ICD (Incremental Cycle Detection) 算法,可以以一種增量式的方式進行檢查,有興趣的讀者可以查看我們的論文[1]。
第三步,如果在一致性檢查中發現有不一致的情況 (即找到了環),這時需要找出不一致的原因,并且以沖突子句的形式報告給 Core Solver。有關沖突子句生成的工作,有興趣的讀者可以查看我們的論文[1]。
# 一些擴展 #
上面只討論了不含分支的簡單并發程序和 SC 內存模型,上述方法還可以很容易地被擴展到更復雜的程序和更一般的內存模型中。
# 針對分支和循環程序的擴展
分支的處理很簡單,對應于每條賦值語句加入一個守護條件即可。循環的處理跟串行程序類似,要么引入一個循環不變式,要么將循環展開。不贅述。

# 針對弱內存模型的擴展
弱內存模型與強內存模型的主要區別在于,線程的訪存操作最后被執行的順序與線程發出來的順序可能不一致,由此會導致更多的不確定性。前面已經提到,在順序一致性模型下,并發程序的執行空間已經遠大于同等規模下串行程序的執行空間;在弱內存模型下,程序的執行空間將再經歷一次爆炸式增長。按照傳統的基于執行空間顯式遍歷的方法,弱內存模型下的程序驗證將變得異常復雜。
而我們的方法只需要很小的變動就能適應弱內存模型 (這里主要討論TSO 和 PSO) 的并發程序驗證。
首先,弱內存模型的符號化編碼只需要很小的改動。在所有涉及到的有關程序執行的偏序關系中,弱內存模型只會改變 PO 序。更確切的講,弱內存模型只會松弛掉 PO 中的若干序關系 (具體松弛哪些關系跟所采用的具體的弱內存模型有關),記松弛后的 PO 為 PPO (Preserved Program Order)。編碼中,只需要用 PPO 去替代原來的 PO 就可以了,其他的編碼都無需變動。具體細節請參看我們的論文[2]。

其次,我們的方法還可以很容易的被擴展以考慮并發程序的原子性。我們可以給程序中的某個代碼塊打上原子標簽,然后規定該代碼塊在執行過程中不能被其他線程打斷。原子塊中的指令是被 “打包在一起” 執行的,也就是說,在原子塊外其他指令看來,原子塊中的指令是同時發生的。
于是我們引入等價關系來刻畫原子性。注意等價關系與偏序關系的不同,偏序關系代表兩個事件前后發生,而等價關系代表兩個事件同時發生。體現到符號事件圖上,偏序關系用有向邊表示,而等價關系則用無向邊表示。

最后,弱內存模型的判定過程也不一樣,主要區別在于一致性公理。在順序一致性模型下,我們需要檢查 4 種偏序關系的并集 是否無環。在弱內存模型下,尤其是帶有原子性約束的弱內存模型下,一致性檢查就沒有這么簡單了。具體的一致性公理這里不贅述,有興趣的讀者可以參考我們的論文[2]。需要指出的是,雖然弱內存模型下的一致性公理比之前更復雜,但從判定過程來看,只需要對一致性判定算法進行改動,整個判定過程的框架跟前面還是一樣的。

# 判定過程的進一步優化 #
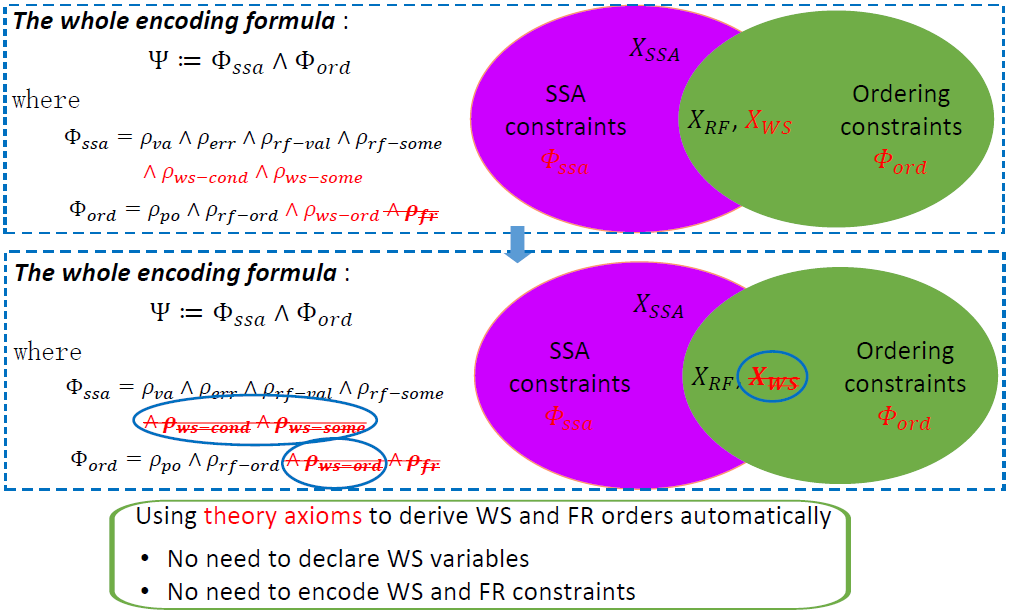
第一個優化是 把更多的推理挪到 SMT 端。
在基本的 理論里面,只把 FR 推理放到了 SMT 端去執行,帶來的好處就是前端不再需要編碼 FR 約束,并且 FR 推理可以按需進行,導致 SMT 求解效率的大大提升。
進一步考慮將 WS 推導也放到后端。在前面所述 三大公理的基礎上,進一步給出WS 公理:給定兩個寫操作 ,和一個讀操作 ,如果已知 的值讀自 (即 ), 發生 (即其守護條件 成立) 且先于 發生 (即 ),則 必定先于 發生 (即 );因為否則 就成為距離 最近的寫,則 應該讀自 而非 。
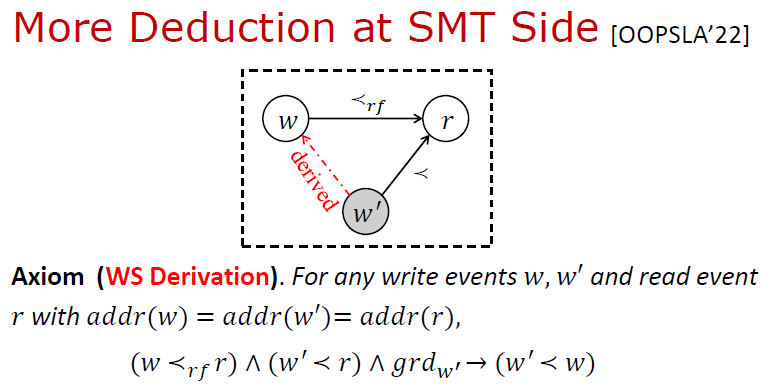
這樣帶來的好處是在前端不再需要引入WS 變量和定義 WS 約束。WS 關系得以在后端以按需的方式進行推理,推理效率得到進一步提升。
第二個優化是 在后端進行傳遞閉包計算。這樣帶來的好處是,之前的一致性檢查需要在符號事件圖中找環,現在只需在圖中找自圈即可。

第三個優化是 預防推理 (Preventive Reasoning)。基本想法是為避免符號事件圖中出現環,提前做一些預防性的推理。
如下圖所示,如果圖中已存在一條從 到 的路徑,那么從 到 就一定不能再連邊了,否則圖上必然出現一個環 (違反一致性公理)。我們借鑒 SAT Solving 中單元子句 (Unit Clause) 的概念,稱 到 的邊為單元邊 (Unit Edge)。在推理過程中,需要避免單元邊被加入到符號事件圖中。注意單元邊可能迭代地由其他一些推理所導出,為了避免單元邊,還要迭代地防止這些推理。
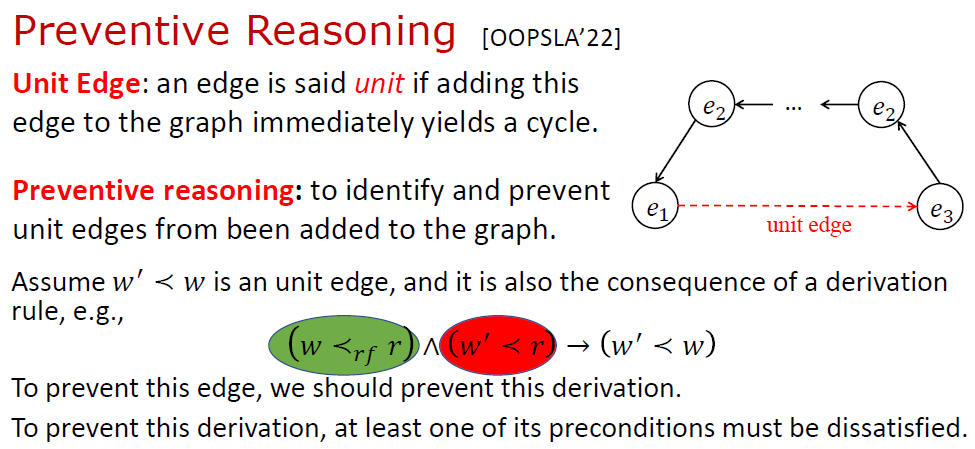
關于預防推理的詳細內容,有興趣的讀者可以查看我們的論文[3]。論文中我們證明了預防推理可以防止任何單元邊被加入到事件圖中,由此帶來的好處是事件圖中永遠不會出現環。

加入預防推理后,Theory Solver 里面不再需要再做一致性檢查和沖突子句生成的工作,只需迭代做 Theory Propagation 即可。
# 工具與實驗:Deagle #
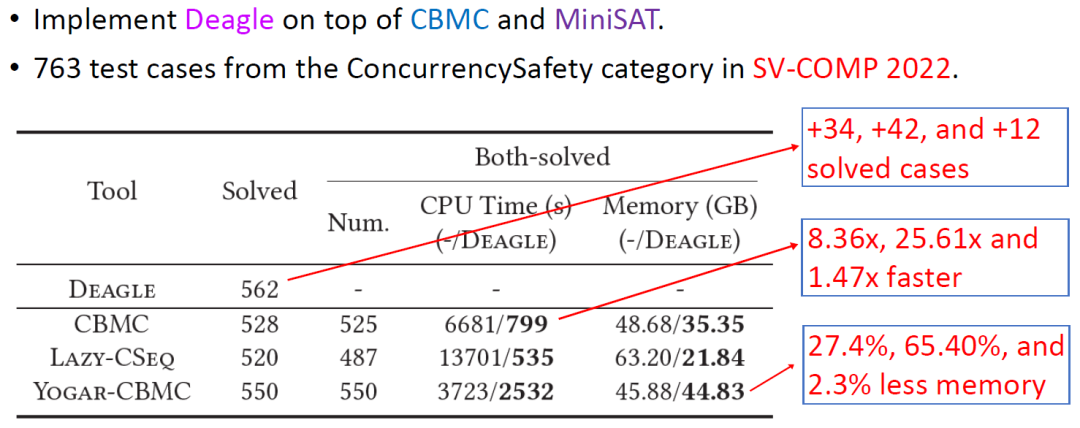
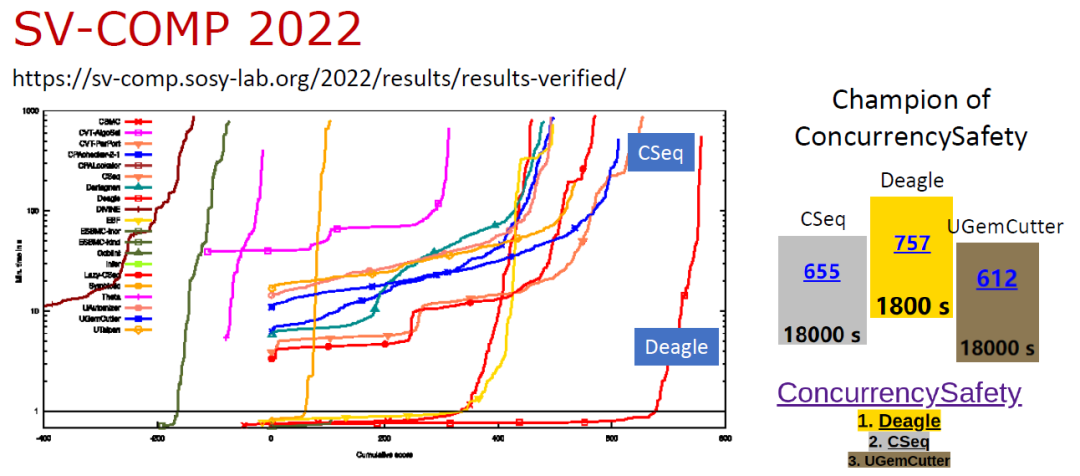
基于上述理論,我們開發了并發程序驗證工具 Deagle[4],參加國際軟件驗證大賽 SV-COMP 2022 并取得了并發安全賽道第一名[5],效率上遠遠優于其他方法。
Evaluation
SV-COMP 2022
# 總結#
我們對并發程序驗證進行了一些探索,引入了一種基于偏序關系的符號化編碼方法;提出了針對并發程序的序關系一致性理論,也針對這個理論開發了專屬的 SMT 判定算法;開發的并發程序驗證工具取得了不錯的效果。
以上。
審核編輯:劉清
-
smt
+關注
關注
40文章
2883瀏覽量
69061 -
Compa
+關注
關注
0文章
4瀏覽量
7836 -
編碼
+關注
關注
6文章
935瀏覽量
54765 -
PSO
+關注
關注
0文章
49瀏覽量
12921 -
SSA
+關注
關注
0文章
8瀏覽量
2948
原文標題:并發程序驗證中的約束求解問題
文章出處:【微信號:編程語言Lab,微信公眾號:編程語言Lab】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一種用于隨機約束仿真的SAT增強的字級求解器

面向多核處理器的低級并行程序驗證
基于改進DE算法的難約束優化問題的求解
基于約束滿足的煉鋼批量計劃的制定方法
設計驗證中的隨機約束
基于SMT求解器的程序路徑驗證方法
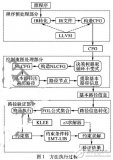
程序驗證研究綜述
一種改進灰狼優化算法的用于求解約束優化問題
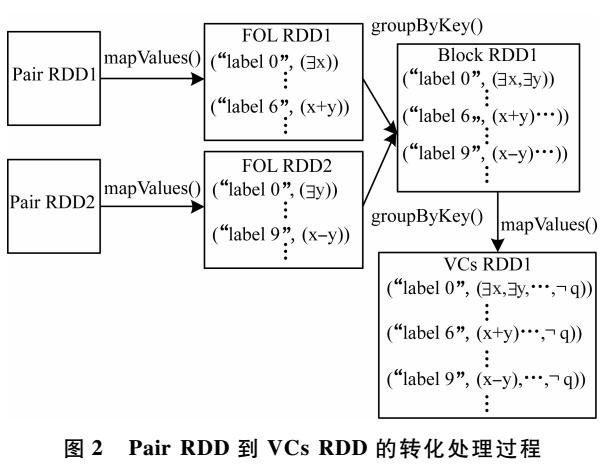
求解#SMT問題的局部搜索算法
一種分布式限界模型檢測方法
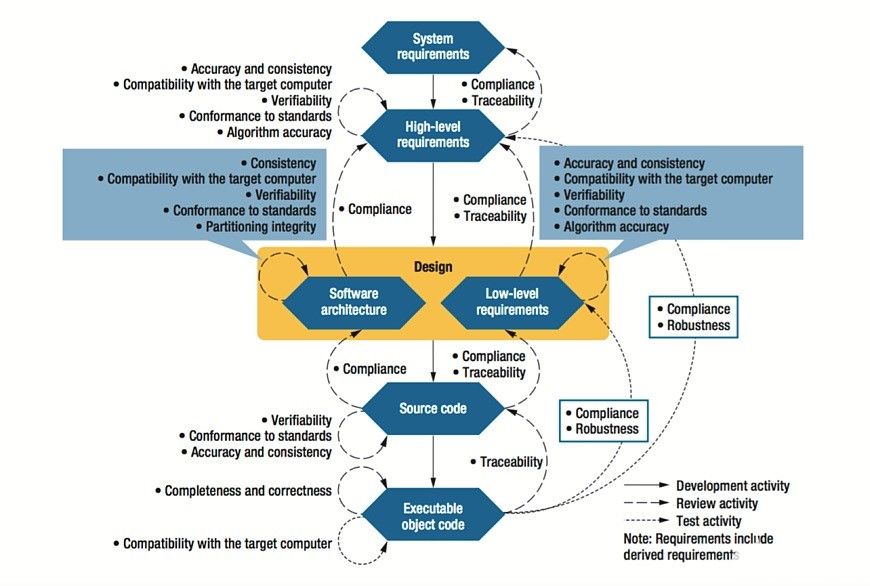
過度約束正式的財產驗證(FPV)會有什么影響
航空電子認證中的正式程序驗證
使用信賴域法求解無約束優化問題
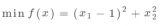




 基于SMT的并發程序驗證中約束求解問題
基于SMT的并發程序驗證中約束求解問題










評論