Part2 ·非線性系統求解算法

三、非線性系統求解算法

非線性系統求解難點在于，即在任何平衡構型下，切線剛度矩陣的計算取決于結構的變形幾何形狀和單元的內力（見part1剛度矩陣推導）。這些屬性是從節點位移獲得的，但節點位移是未知數。因此，無法解析求解平衡方程組，需要運用數值方法進行處理。

求解非線性方程組追蹤平衡路徑可分為單步法和增量迭代法，本文重點介紹增量迭代法。該方法將總載荷分解為一系列增量步，通過增量線性系統的直接或迭代求解獲得相應載荷增量步的位移增量。因此，通過每一步中的一個或幾個線性分析來近似施加載荷和節點位移之間的非線性關系。

求解非線性平衡系統的兩類增量方法：第一種是純增量或單步方法，其中使用單個剛度矩陣來表示每個分析步驟中的載荷位移關系。第二種是增量迭代法，它執行多次線性分析，在每一步迭代求解增量系統，以便在數值公差范圍內收斂到平衡解。本文主要針對增量迭代法進行講解。

1、增量迭代法求解公式

為了追蹤平衡路徑，必須以增量方式多次求解非線性方程組。非線性解通過每個增量的線性響應來近似。線性近似在線性化解和實際非線性解之間產生殘差。該殘差通過通過迭代進行收斂校正。在后文中，增量步i-1對應的構型是最新獲得的平衡配置，而增量步 i 對應的構型是當前未知的需要求解的構型，符號Δ用來表示變量在每個增量步步的增量，符號δ表示每次迭代的增量。 切線剛度矩陣 K 在下式中定義，即內力對上一步對應的平衡構型下的節點位移的導數。

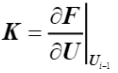?（26）

因此，內力表式為

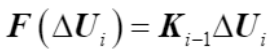?（27）

求解位移增量的增量系統表達式為，其中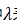表示荷載比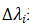，表示第i增量步荷載比增量，與總荷載乘積即為荷載增量

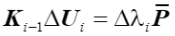（28）

梁單元的切線矩陣的推導在part1中通過虛擬位移原理、運動學描述（更新拉格朗日法或共旋法）和有限元方法來離散每個單元位移場來得到。然而，由于內力是位移的非線性函數，方程的線性化增量系統的解不滿足平衡。即外力和內力之間的不平衡，產生了殘余力矢量。在每個增量中通常采用迭代過程，以通過消除殘余力來確保平衡。

以上是增量步的解釋，接下來對迭代步進行講解。 考慮到結構在第 i-1 步處于平衡狀態，希望在第 i 步達到平衡。為了消除源自線性化增量的殘余力，通過在每個增量步驟中執行Newton-Raphson之類的校正迭代來完成的，直到滿足收斂標準并建立新的平衡狀態。

在每次迭代中，由下標 j = 1,2,3... 表示，得到對應迭代步的載荷比增量 δλij 和節點位移增量δUij。這些迭代增量表示相應步驟中載荷和位移值的校正。因此，在第j次迭代之后，通過累加迭代增量來更新第i步的總增量，如下式所示：

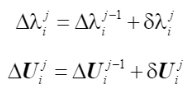（29）

基于上述迭代步對荷載和位移增量的修正，整個分析的載荷比和節點位移的總值更新如下：

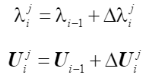（30）

在第 j 次迭代后得到殘余力矢量，由外部和內部節點力的總值之間的差值給出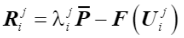： （31）

基于上述殘余力矢量，可根據下式求得在第i步的第j次迭代中位移迭代增量

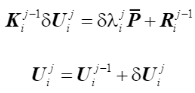（32）

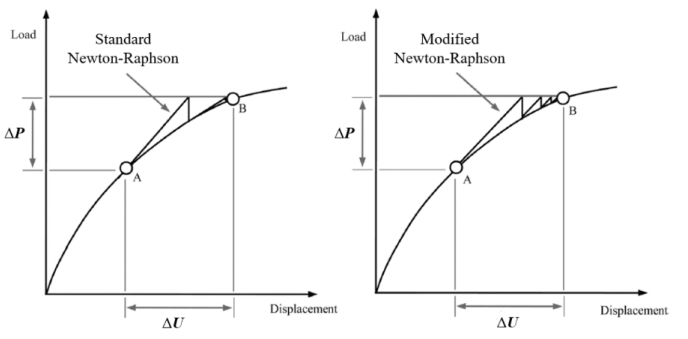
圖12

上述迭代算法最常用的是Newton-Raphson迭代算法，如圖12所示，標準 Newton-Raphson 迭代算法的切線剛度矩陣在所有迭代步都會進行更新，考慮大型系統時矩陣更新會耗費較多計算資源，因此可使用修正Newton-Raphson 算法，切線矩陣僅在每個增量步驟的開始進行計算，并在所有后續迭代中保持不變，即，對于 j > 1。修正Newton-Raphson 算法具有較低的計算成本每次迭代都比標準版本，但收斂通常較慢，因為它通常需要在每個增量步驟中進行更多的迭代，但相較切向剛度矩陣更新耗費的資源來說還是值得的。對于上述方程x求解來說，因為存在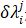這個未知量，因此還需要一個附加方程來與之組成方程組進行求解，這個附加方程的一般形式為

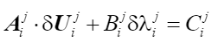（33）

式中向量A和標量 B 和 C 是常數，可以根據不同的求解方法采用不同的值。上式x與組成的方程組寫成矩陣形式為

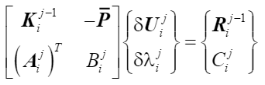（34）

由于上述等式左端的矩陣不再是對稱矩陣，所以在做大型計算時存儲和計算上效率都會明顯降低，為了克服這個問題，Batoz & Dhatt (1979) 提出了一種技術來克服這個問題，方法是將系統分解為兩個使用原始切線剛度矩陣的系統，因此原始系統的帶狀和對稱特性保持不變，具體如下所示

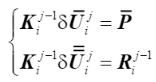（35）

位移迭代增量的解是上述切線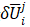增量和殘差增量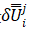增量的線性組合：

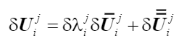（36）

其中迭代步j對應的荷載比增量可通過下式求得

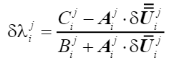（37）

上述增量迭代法求解所用到的公式總結如下表所示

?

（1）增量迭代法求解步驟

上述增量迭代求解可分為兩個階段，分別為預測階段和校正階段。預測階段相當于第一次迭代，其余迭代屬于校正階段。

① 預測階段

在每個增量步，首先執行預測階段的迭代。目的是使用上一步得到的切線剛度矩陣進行單次線性分析來計算預測解。具體來講，這一階段，對于第i個增量步，首先要進行初始切線剛度矩陣的計算，直接基于上一步結束時獲得的結果（即節點位移 和內力對應的剛度矩陣）。

然后根據方程（35）通過線性分析計算位移的切線增量 。該階段的殘余位移增量為零，因為忽略了來自上一步的殘余力。位移的預測增量，，可根據方程(36)獲得。但僅是位移的切線增量乘以載荷比的增量。載荷比增量是用約束方程（37）計算得到的，該約束方程定義了一個超曲面來限制增量迭代方法的校正解。下圖13為單自由度系統的預測階段示意圖。

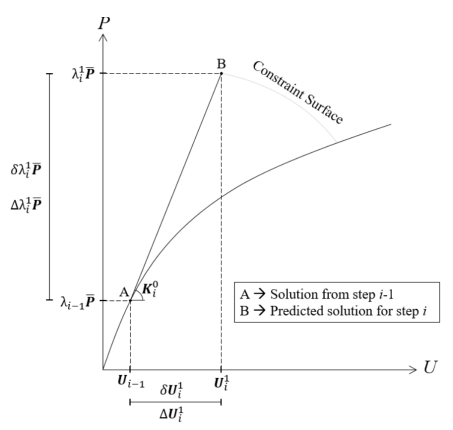
圖13

因此預測階段的求解的核心目的就是計算預測荷載比增量。在某分析過程的第一個增量步的預測階段荷載比增量須人為指定，一般為最大荷載的10%~20%。在接下來的迭代過程中，荷載比增量則由約束方程（37）所定義的迭代算法進行計算，后文荷載比增量的計算方法本質就是對約束方程（37）的定義。

預測階段荷載比增量對求解有很大的影響，直接與收斂性相關。該階段，荷載比增量過大可能導致收斂問題，荷載比增量過小耗費計算資源，精度的提高也有限。因此使得程序能夠自動根據非線性程度調整預測階段的荷載比增量是一個優秀的非線性算法所應具備的功能。

即當結構響應基本程線性時，提高增量，當非線性較大時，減小增量。而且當求解至荷載極限點達到一個即將失穩的平衡態時，所追蹤的位移增量對應的荷載增量必須是負值才符合常理，因此算法還應能夠判斷增量正負的選擇。

a、預測階段荷載比增量計算方法

荷載比增量的計算取決于約束方程（37）的定義，本節計算方法本質即約束方程的定義。兩種計算預測階段荷載比增量的方法，一種基于迭代次數的計算方法，另一種是根據系統剛度的計算方法。本文重點針對第一種方法進行介紹。基于迭代次數的計算方法計算預測階段荷載比增量的方法又可以分為三類：

荷載增量法；

外力功增量法；

弧長增量法。

我們重點介紹第三種弧長增量法，因為弧長法的優勢在于在于可以追蹤平衡路徑，準確捕捉snap-through和snap-back現象，如圖14所示。為了數值算法上增量步大小一致性，校正階段也采用同類型的弧長法。弧長法公式具體推導過程大家可參考相關文獻，這里只列出用圓柱弧長法和球形弧長法計算預測階段荷載比增量的最終公式

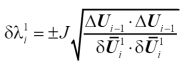（38）

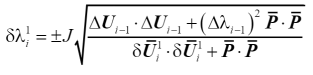（39）

其中J為迭代調整因子，表達式如下

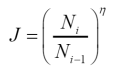（40）

式中，Ni 和 Ni-1 分別是當前增量步所需的迭代次數，以及前一增量步中實現收斂的迭代次數。指數變量 η 通常在 0.5 到 1.0 的范圍內，但通常采用較低的值。

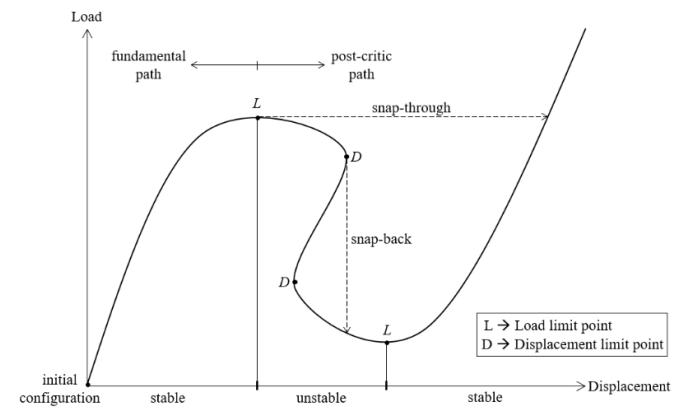
圖14 b、預測階段荷載比增量符號計算方法

上文提到預測階段的求解的核心目的除了需要確定荷載比增量大小外，另一個重要的工作就是完成荷載比增量正負符號的確定。確定荷載比增量符號最常見方法的是基于剛度參數的行為進行確定，這些剛度參數常見的有 CSP（Current Stiffness Parameter）和 GSP（Generalized Stiffness Parameter）。因為參數CSP會在位移極限點附近出現一些數值不穩定性，所以本文主要介紹更為通用的GSP參數。GSP的具體表達式為

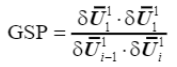?（41）

可以看出，GSP參數的分子是一個正數，分母由當前和前一步位移向量的標量積給出，該標量積的符號可以反應前一步和當前步的增量是否在同一個“方向”上，如果同向則為正，如果反向則為負，如圖 15所示。當兩個增量步之間存在荷載極限點時，兩個位移向量的方向是不同的，因此GSP<0。因此，每次 GSP為負值時，必須反轉預測階段的荷載比增量的符號。增量符號可根據下式確定，其中初始增量步假定增量符號為正值。

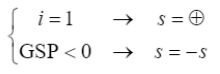（42）

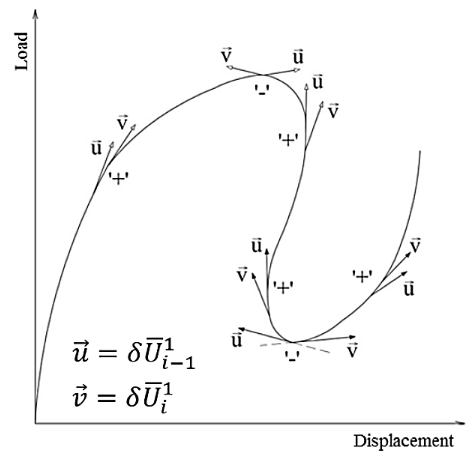
圖15

（2）迭代矯正階段

增量迭代方法的校正階段旨在通過迭代循環消除由預測階段產生的殘余力來恢復結構平衡。該迭代循環從更新總荷載比和總節點位移 開始，將預測增量（和 ）添加到上一步的結果（ 和 ）。隨著幾何構型的更新，相應的內力 被計算出來，殘余力可以通過外部和內部節點力之間的差異來獲得。

檢查迭代是否收斂的方法，最常見的是基于殘余力、殘余位移或這些殘余結果產生的功。本文采用的收斂標準是基于力的檢查，如下式所示

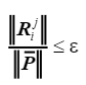（43）

式中，分子分母分別為殘余力矢量和參考載荷矢量的歐幾里得范數，，該比率必須低于給定的容差ε，通常在 10-5 到 10-3 的數量級。如果滿足收斂，則預測解被認為平衡狀態，可致性下一增量步，否則開始第一次校正迭代。 每次校正迭代的第一個過程是計算切線剛度矩陣，要根據最新構型的節點位移和內力來對剛度矩陣進行更新。如果采用修正Newton-Raphson 迭代方案，則跳過此步驟，并使用在預測階段的切線矩陣。如方程(35)所示，位移的切線增量和殘余增量分別用參考載荷矢量和最后獲得的殘余力矢量計算。

然后，根據相應的約束方程（37）計算載荷比的迭代增量。最后，用方程(36)得到位移的迭代增量。。 載荷比和位移的迭代增量取決于約束方程（37）定義的超曲面。如果執行的迭代不僅涉及位移修正，還涉及載荷比的修正，則稱為連續法，因為它可以跟蹤超出極限點的平衡路徑，例如上小節提到的弧長法。在這種情況下，控制修正解的約束面在一個或多個點處與平衡路徑相交。

獲得修正解后，接下來的程序與檢查預測解的收斂性相同：更新載荷比和節點位移的總值，計算外力、內力和殘余力，最后檢查當前迭代解的收斂性。圖16 給出了所描述過程的示意圖。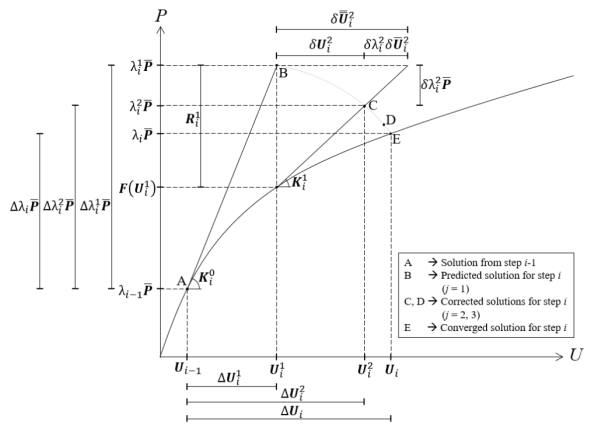

圖16

與預測階段的荷載比計算方法相對應，迭代階段的荷載比增量計算方法同樣有荷載控制法、外力功控制法和弧長控制法（還有其他多種方法，就不一一列舉）。

傳統的牛頓拉普森迭代法本質就是荷載增量控制法，在每個增量步中使用固定量的荷載比增量即預測階段的荷載增量，并在每次迭代后保持不變。執行校正迭代僅通過位移校正來滿足平衡要求，如下圖17所示。

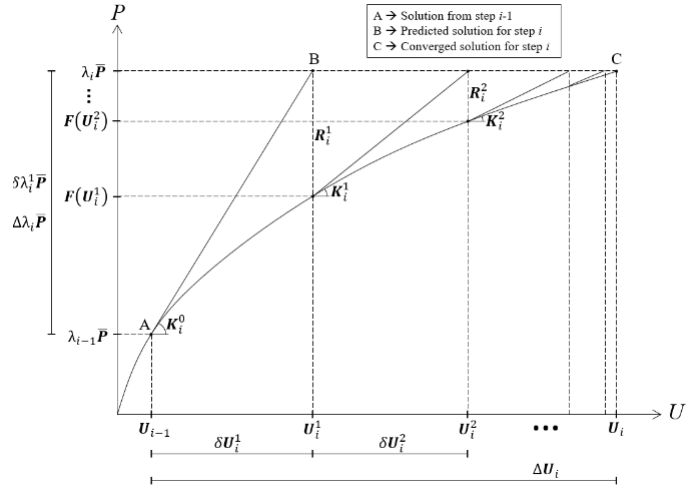
圖17

當試圖解決荷載極限點問題時，這種方法的存在明顯的缺陷。一旦在預測階段定義了固定荷載比增量，如果在增量中出現極限點，就無法修改荷載矢量。

盡管可減小的載荷比增量使其緩慢地接近極限點，但由此產生的剛度矩陣接近奇異的性質使得難以追蹤結構的后極限狀態響應。圖 18 顯示了使用荷載增量控制法跟蹤具有snap-though行為的系統的平衡路徑時的典型結果。

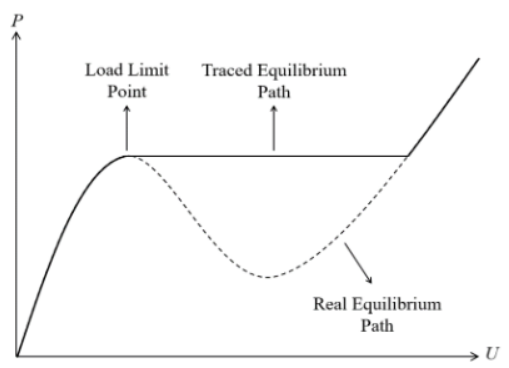
圖18

本文重點介紹適應度較強的弧長控制法，弧長法的優勢在于在于可以追蹤平衡路徑，準確捕捉snap-through和snap-back現象。由于弧長法也分多種，如線性弧長法和恒定弧長法。這里僅介紹恒定弧長法，即由位移和載荷增量的范數定義的弧長增量 ΔL 在整個迭代過程中保持不變。推導過程省略，這里直接給出恒定圓柱弧長法計算迭代步荷載比增量的公式

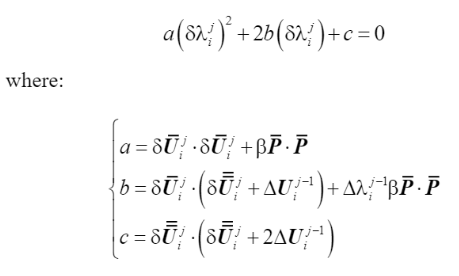（44）

求解上式可得迭代步荷載比增量的顯式表達式

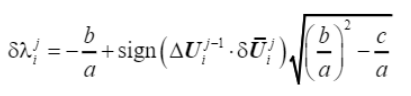（45）

審核編輯：劉清