摘要
深度網(wǎng)絡(luò)在從大量數(shù)據(jù)中學(xué)習(xí)模式方面表現(xiàn)出色。另一方面,許多幾何視覺任務(wù)被指定為優(yōu)化問題。
為了將深度學(xué)習(xí)和幾何視覺無縫地結(jié)合起來,至關(guān)重要的是進(jìn)行端到端的學(xué)習(xí)和幾何優(yōu)化。
為了實(shí)現(xiàn)這一目標(biāo),我們提出了BPnP,這是一個(gè)新穎的網(wǎng)絡(luò)模塊,通過Perspective-nPoints(PnP)求解器反向傳播梯度,以指導(dǎo)神經(jīng)網(wǎng)絡(luò)的參數(shù)更新。
基于隱式微分,我們表明一個(gè) "獨(dú)立的 "PnP求解器的梯度可以被準(zhǔn)確有效地導(dǎo)出,就像優(yōu)化器塊是一個(gè)可微分的函數(shù)。
我們通過將BPnP納入一個(gè)深度模型來驗(yàn)證它,該模型可以從訓(xùn)練數(shù)據(jù)集中學(xué)習(xí)相機(jī)的內(nèi)在因素、相機(jī)的外在因素(姿勢(shì))和三維結(jié)構(gòu)。
此外,我們開發(fā)了一個(gè)用于物體姿勢(shì)估計(jì)的端到端可訓(xùn)練管道,該管道通過將基于特征的熱圖損失與二維-三維重投影誤差相結(jié)合,實(shí)現(xiàn)了更高的準(zhǔn)確性。
由于我們的方法可以擴(kuò)展到其他優(yōu)化問題,我們的工作有助于以一種原則性的方式實(shí)現(xiàn)可學(xué)習(xí)的幾何視覺。
主要貢獻(xiàn)
我們的主要貢獻(xiàn)是一個(gè)名為BPnP的新型網(wǎng)絡(luò)模塊,它包含了一個(gè)PnP求解器。BPnP通過PnP "層 "反向傳播梯度,以指導(dǎo)神經(jīng)網(wǎng)絡(luò)權(quán)重的更新,從而利用既定的目標(biāo)函數(shù)(二維-三維重投影誤差的平方和)和幾何視覺問題的求解器實(shí)現(xiàn)端到端的學(xué)習(xí)。
盡管只結(jié)合了一個(gè)PnP求解器,我們展示了BPnP如何被用來學(xué)習(xí)有效的深度特征表征,用于多種幾何視覺任務(wù)(姿勢(shì)估計(jì)、運(yùn)動(dòng)結(jié)構(gòu)、相機(jī)校準(zhǔn))。
我們還將我們的方法與最先進(jìn)的幾何視覺任務(wù)的方法進(jìn)行比較。從根本上說,我們的方法是基于隱式微分的。
主要方法
反向傳播的PnP算法: 讓g表示一個(gè) "函數(shù) "形式的PnP求解器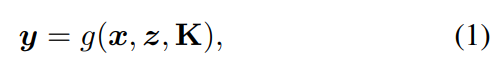
從n個(gè)2D-3D的對(duì)應(yīng)關(guān)系中返回?cái)z像機(jī)的6DOF姿態(tài)y和其內(nèi)部參數(shù)K∈R3×3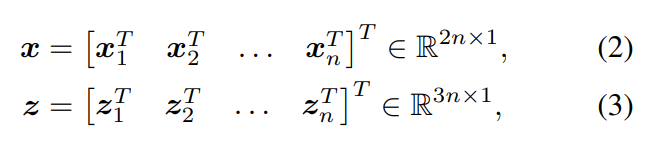
其中(xi , zi)是第i個(gè)對(duì)應(yīng)關(guān)系。讓?duì)?-|y, K)是三維點(diǎn)在圖像平面上的投影變換,姿態(tài)為y,相機(jī)本征為K。
從本質(zhì)上講,g的 "評(píng)估 "需要解決優(yōu)化問題如下: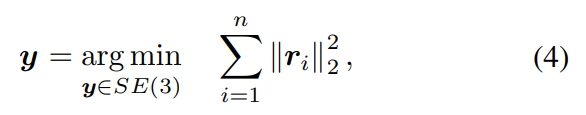
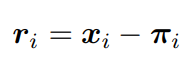
ri表示第i對(duì)對(duì)應(yīng)關(guān)系的重投影誤差。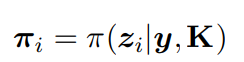
πi是三維點(diǎn)zi在圖像平面上的投影。
我們的最終目標(biāo)是將g納入一個(gè)可學(xué)習(xí)的模型中,其中x、z和K可以是一個(gè)深度網(wǎng)絡(luò)的(中間)輸出。此外,公式(4)的求解器應(yīng)該被用來參與網(wǎng)絡(luò)參數(shù)的學(xué)習(xí)。為此,我們需要把g當(dāng)作一個(gè)可微調(diào)的函數(shù),這樣它的"梯度 "就可以反向傳播到網(wǎng)絡(luò)的其他部分。接下來我們將詳細(xì)介紹如何對(duì)反向傳播的梯度進(jìn)行計(jì)算。
1. 隱式函數(shù)定理(IFT) 這里簡(jiǎn)單公式推導(dǎo)了IFT隱式函數(shù)定理。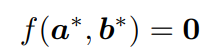
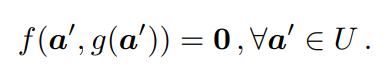
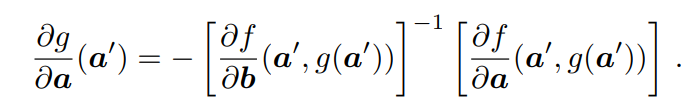
IFT允許計(jì)算一個(gè)函數(shù)g相對(duì)于其輸入a的導(dǎo)數(shù),而不需要函數(shù)的明確形式,但有一個(gè)函數(shù)f約束a和g(a)。
2. 構(gòu)造約束函數(shù)f
為了調(diào)用隱式微分的IFT,我們首先需要定義約束函數(shù)f(a, b)。對(duì)于我們的問題,我們使用所有四個(gè)變量x、y、z和K來構(gòu)造f。
但我們將f視為一個(gè)雙變量函數(shù)f(a, b),其中a在{x, z, K}中取值--取決于要得到的偏導(dǎo)--而b=y(即g的輸出姿勢(shì))。
為了維護(hù)約束函數(shù)f(a,b),我們利用了優(yōu)化過程的靜止約束。
在這里,將PnP求解器的目標(biāo)函數(shù)g表示為: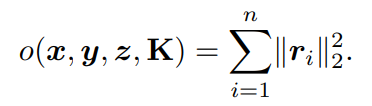
由于PnP求解器的輸出姿態(tài)y是目標(biāo)函數(shù)的局部最優(yōu),所以可以通過對(duì)目標(biāo)的一階導(dǎo)數(shù)與y的關(guān)系來建立一個(gè)靜止約束,即: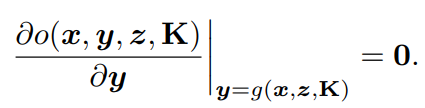
給出一個(gè)PnP求解器的輸出姿勢(shì)y = [y1, ..., ym] T,我們構(gòu)建f,可以寫為: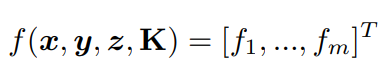
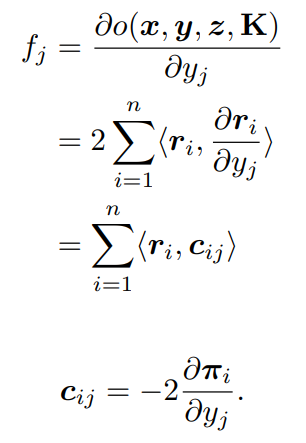
3. 前向和反向傳播
我們對(duì)g的PnP公式基本上是執(zhí)行最小二乘法(LS)估計(jì),這對(duì)離群值(x、z和K的惡劣誤差)并不穩(wěn)健。
另外,我們可以采用一個(gè)更穩(wěn)健的目標(biāo),如加入M-估計(jì)器[56]或使離群值的數(shù)量最大化[15]。
然而,我們的結(jié)果表明,LS實(shí)際上更合適,因?yàn)樗鼘?duì)輸入測(cè)量中的誤差的敏感性鼓勵(lì)學(xué)習(xí)快速收斂到不產(chǎn)生x、z和K中的異常值的參數(shù)。
相反,一個(gè)穩(wěn)健的目標(biāo)會(huì)阻止異常值的誤差信號(hào),導(dǎo)致學(xué)習(xí)過程不穩(wěn)定。
鑒于(4),解算器的選擇仍然存在。
為了進(jìn)行隱式微分,我們不需要精確地解決(4),因?yàn)閏ij只是(4)的靜止條件,任何局部最小值都能滿足。
為此,我們采用Levenberg-Marquardt(LM)算法,該算法保證了局部收斂。
作為一種迭代算法,LM在求解(4)時(shí)需要初始化y(0)。
我們通過將(1)重寫為:"(1)"來明確這種依賴關(guān)系: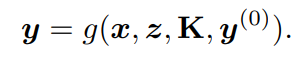
在反向傳播中,我們首先構(gòu)建f,然后得到g相對(duì)于其每個(gè)輸入的雅可比系數(shù),即: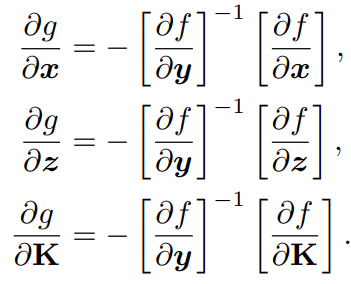
給出輸出梯度,BPnP返回輸入梯度: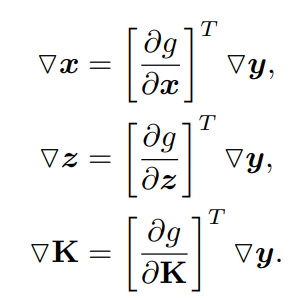
算法流程如下圖所示:
主要結(jié)果: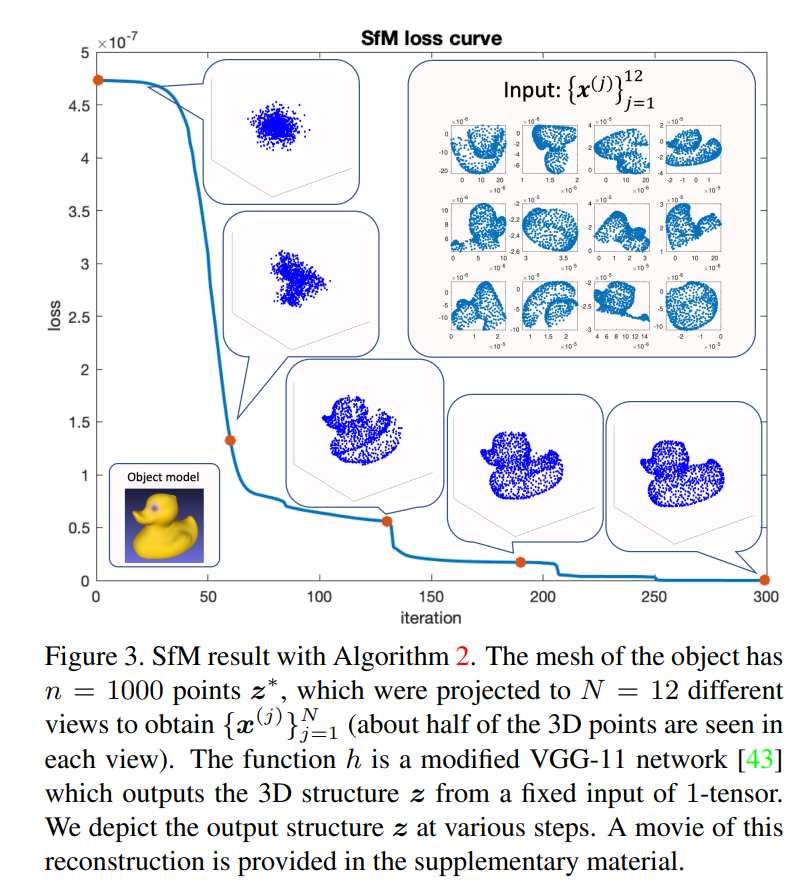
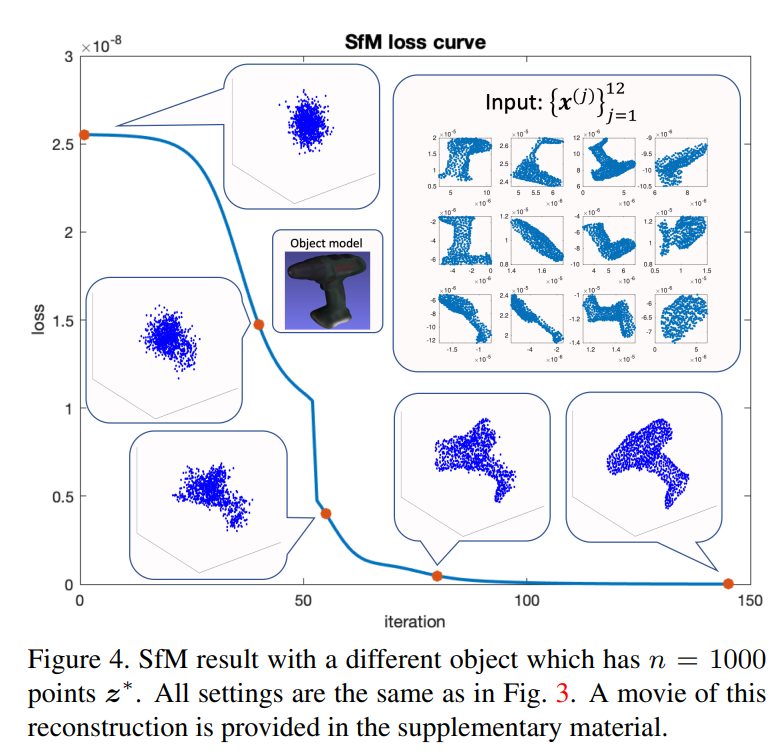
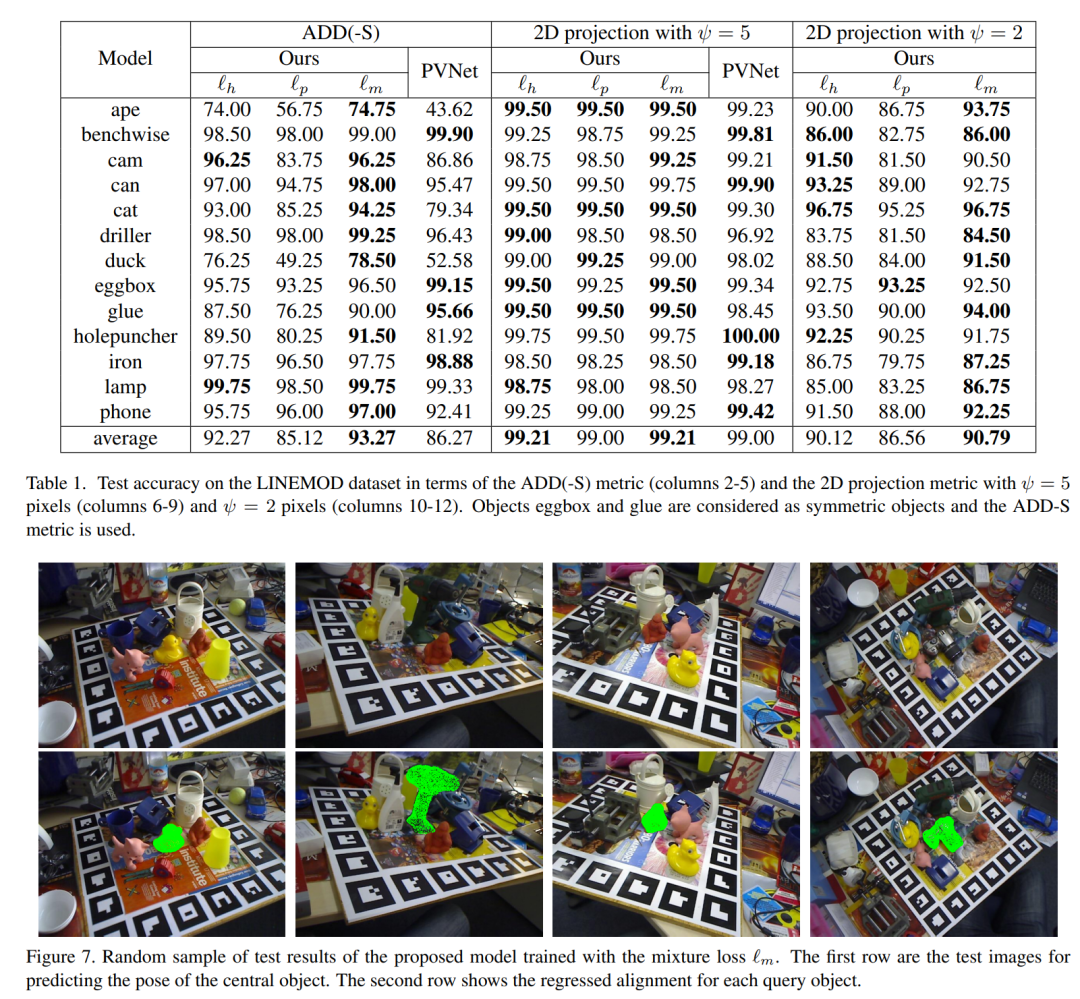
審核編輯:劉清
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4765瀏覽量
100565 -
網(wǎng)絡(luò)模塊
+關(guān)注
關(guān)注
0文章
26瀏覽量
9295 -
求解器
+關(guān)注
關(guān)注
0文章
77瀏覽量
4516
原文標(biāo)題:BPnP:基于反向傳播PnP優(yōu)化的端到端可學(xué)習(xí)幾何視覺
文章出處:【微信號(hào):3D視覺工坊,微信公眾號(hào):3D視覺工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于WiMAX接入技術(shù)的端到端網(wǎng)絡(luò)架構(gòu)
反向傳播算法的工作原理
端到端的自動(dòng)駕駛研發(fā)系統(tǒng)介紹
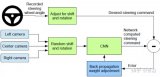
基于深度神經(jīng)網(wǎng)絡(luò)的端到端圖像壓縮方法

基于生成式對(duì)抗網(wǎng)絡(luò)的端到端圖像去霧模型

結(jié)合深度學(xué)習(xí)的自編碼器端到端物理層優(yōu)化方案
BP(BackPropagation)反向傳播神經(jīng)網(wǎng)絡(luò)介紹及公式推導(dǎo)

一種對(duì)紅細(xì)胞和白細(xì)胞圖像分類任務(wù)的主動(dòng)學(xué)習(xí)端到端工作流程
神經(jīng)網(wǎng)絡(luò)反向傳播算法的優(yōu)缺點(diǎn)有哪些
端到端測(cè)試用例怎么寫
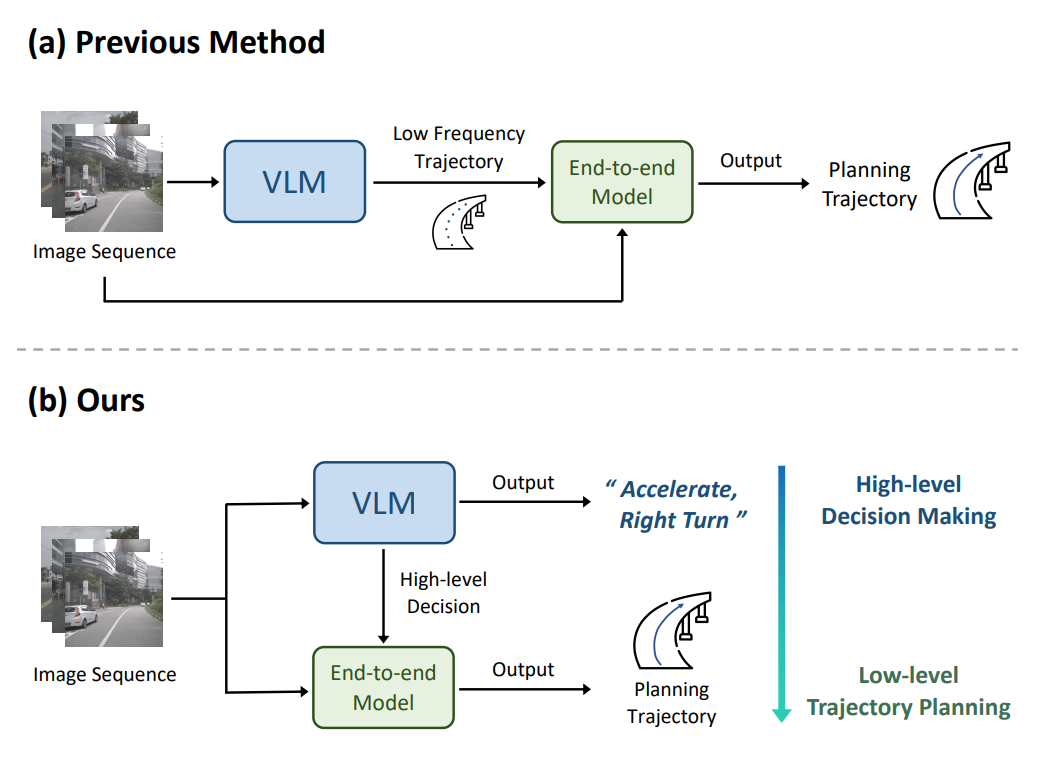
連接視覺語言大模型與端到端自動(dòng)駕駛




 基于反向傳播PnP優(yōu)化的端到端可學(xué)習(xí)幾何視覺介紹
基于反向傳播PnP優(yōu)化的端到端可學(xué)習(xí)幾何視覺介紹











評(píng)論