這篇文章來源于DevicePlus.com英語網站的翻譯稿。

點擊此處閱讀本文的第1部分>

在Arduino DSP系列的第二部分中，我們將繼續深入研究數字信號處理的基礎知識。我們將學習數字濾波器的特性以及在MATLAB中處理信號時如何應用這些特性。在下一篇文章中，我們將制作一期有關傅里葉變換的深入教程，并研究語音信號最重要的參數：頻率。

軟件

Matlab

第1步：如何將信號導入 Matlab

用Audacity錄制語音信號后，現在是時候在MATLAB中進行處理了。此功能可以通過 wavread函數完成，該函數負責讀取（.wav）聲音文件。Audacity的輸出信號具有此擴展名。此函數的輸入是信號名稱（testSound.wav），在MATLAB函數中，您只需要寫“testSound”即可。該函數的輸出如下所示：

Y – 信號名稱

Fs – 信號的采樣率

Bits – 位數

我們可以使用以下代碼實現此函數。該代碼還能夠播放聲音，讓用戶在信號處理過程中聽到信號如何隨時間變化。

[s0,fs,bits] = wavread('testSound'); 
sound(s0,fs);
pause(9) 
t=(0:length(s0)-1)/fs; 
figure
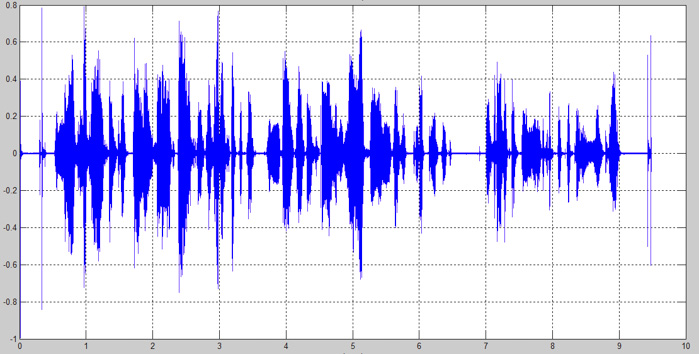
plot(t,s0),grid  
title('The initial signal.'); 
xlabel ('tTime')
ylabel('s0(n)');

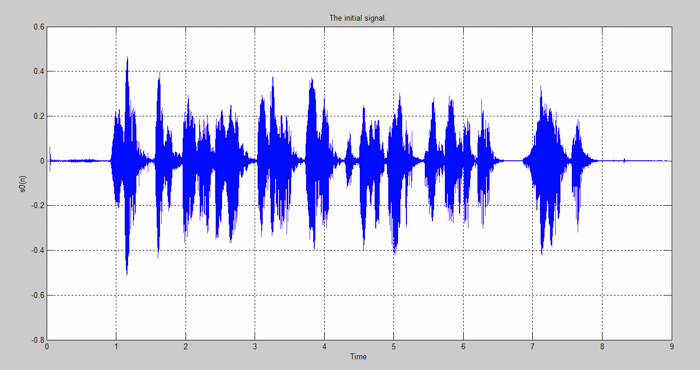
圖1：Matlab中的語音信號

如果您想獲得人聲信號的更多信息，您只需輸入音頻文件名稱（后綴名為.wav），然后函數 audioinfo 就會給您返回聲音參數。

audioinfo('testSound.wav')

此函數非常方便，尤其是當一個信號是未知信號時。比如，如果在處理一個信號時無法確定采樣率、持續時間和位/樣本等必要信息，那么就可以使用上述函數查詢該信號的更多信息。

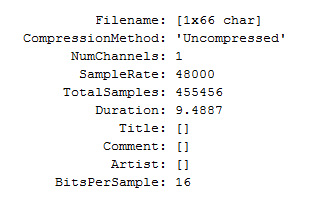
圖2：信號屬性

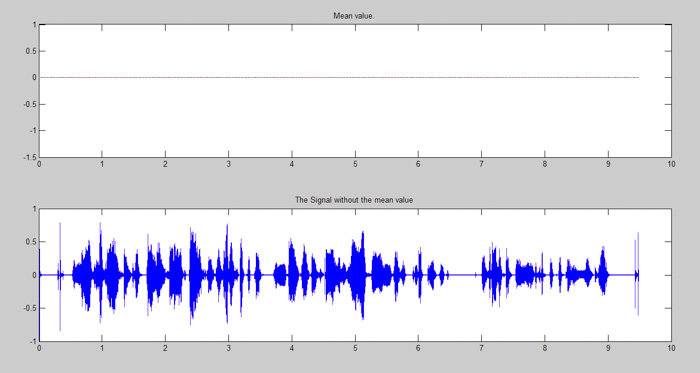
圖3：聲波及其平均值

第2步：去除平均值（或DC分量）

直流（DC）分量是添加到純交流（AC）波形（比如語音信號）的恒定電壓。純AC波形的真實平均電壓為零。語音信號是模擬信號，但是用Audacity將其轉換為數字信號時，會獲得一個DC分量。發生這種情況是因為Audacity擁有自己的范圍并對信號進行了重新調整。通常，模擬信號范圍為-0.5至0.5V。我們需要0.5V的直流分量，這是因為程序使用一系列正數來縮放樣本值（每個樣本值被轉換為從0到N的數字；N是自然數）。

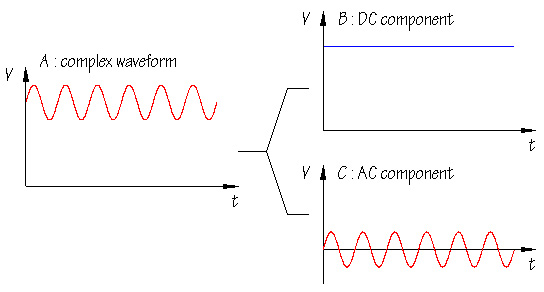
圖4：交流分量和直流分量說明

但是，如果存在DC分量，那么AC的幅度會根據DC分量的值發生變化。我們來看一下 圖 4。假設您有一個幅度為2V峰-峰值的正弦波，同時疊加了一個0.5V的直流分量，那么最終信號的幅度最高為1.5 V，最低為-0.5 V。

我們應該查看一下信號是否具有直流分量，并且要確定直流分量的值。我們可以通過繪制數值來實現，也可以在命令窗口中輸入M實現。

M = mean(s0)
figure
subplot(2,1,1), plot(t,M)  
title('Mean value.'); 
s1 = removeDC(s0);
subplot(2,1,2), plot(t,s1)  
title('The Signal without the mean value');

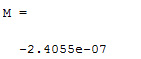
圖5：信號平均值

去除平均分量很重要，因為語音信號本身不含直流分量，而我們希望使用純凈的音頻波形。 removeDC 函數中的以下代碼能夠計算信號的平均值并將其從原始信號中除去。

function [sOut] = removeDC(sInput)
DC = mean(sInput);
    sOut = sInput - DC;
end

第3步：抽取過程

我們的采樣頻率現在為48000Hz，我們希望將其變成16000Hz。通過抽取，我們可以降低信號的采樣率。抽取可以通過MATLAB中的 decimate 函數實現。當我們對一個語音信號進行采樣時，根據奈奎斯特采樣定理，最小頻率應為8kHz——這是因為人類聽覺最大帶寬為4kHz。

這樣做是因為我們想比較原始信號與抽取信號之間的差異，并了解這種修改如何改變原始信號。

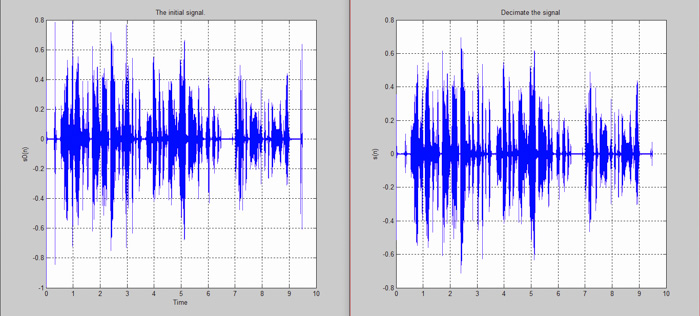
圖6：抽取的信號

進行抽取（或下采樣）時，我們將采樣率修改成較低的速率（與之前的采樣率相比）。如下圖所示，左側模擬信號的采樣率高于右側的模擬信號。這意味著我們對采樣頻率進行抽取。

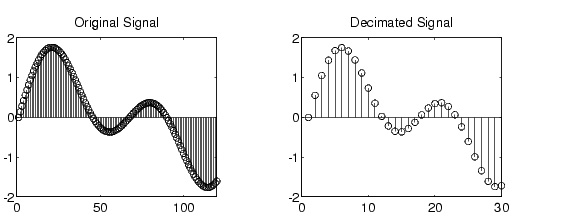
圖 7: 抽取的信號

我們還可以進行上采樣——下采樣的反過程，并增加采樣頻率。這可以通過插值技術和低通濾波器來完成。

fe2=fs/3;
%s2 = decimate(s1,3);  

s2 = decimate(s0,3);
t1=linspace(0,length(s2)/fe2, length(s2));
figure 
plot(t1,s2),grid               
title('Decimate the signal');    
ylabel('s(n)');
sound(s2,fe2);
pause(9)

第4步：信號濾波

簡單來講，數字濾波器是一種離散時間、離散幅度的卷積器。數字濾波器在信號處理中很重要，因為與模擬濾波器相比，它可以處理多個操作。（我們可以假設數字濾波器的成本更高，因為我們需要特殊的數字信號處理器來運行濾波算法的功能。）

每個數字濾波器都有不同的規格：通帶、阻帶和紋波。我們首先回顧一下以下術語。

通帶：一個濾波器允許通過的頻率帶。

截止頻率：用戶選擇的某個頻率，表示可以通過濾波器的理論頻率。為了避免走樣，此頻率必須低于 采樣頻率/2 。在電子學中，截止頻率是指信號功率變小兩倍的頻率值。

阻帶：所有高于此頻段的頻率都無法通過濾波器。

數字濾波器可以分為兩類：FIR（有限脈沖響應），濾波器系數為整數。IIR（無限脈沖響應），具有模擬等效模型，并且階數較低時更有效。

FIR/IIR濾波器最重要的特性之一是相位特性：

FIR: 線性相位特性

IIR:非線性相位特性（或相位失真）

FIR濾波器屬性 – dspGuru by Iowegian International

“線性相位是指濾波器的相位響應是頻率的線性（直線）函數（不包括+/-180度的相位纏繞）。這使得通過濾波器的所有頻率的延遲都相同。因此，這種濾波器不會引起“相位失真”或“延遲失真”。在某些系統中，比如在數字數據調制解調器中，沒有相位/延遲失是FIR濾波器相對于IIR和模擬濾波器的關鍵優勢。”

MATLAB中有眾多類型的數字濾波器可供選擇，但是我們需要了解如何將其應用于我們的具體場景。對于本項目，我們選用IIR濾波器，因為它更有效，即與FIR濾波器相比，我們需要更小的階數。

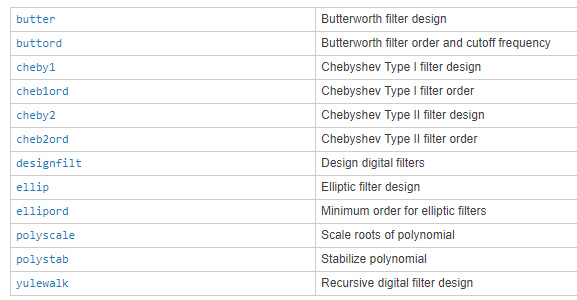
圖 8: IIR 濾波器

以下代碼可以在MATLAB中創建一個Butterworth濾波器。添加濾波器階數和截止頻率后，此函數會返回濾波器系數。

fn = fe2/2; 
fc=3400; % cutoff frequency
[Bd,Ad] = butter(40,3400/fn,'low');

在命令行中輸入 help butter ，就可以通過MATLAB幫助了解為什么采樣率會除以2。“[b,a] = butter(n,Wn)會返回一個n階低通數字Butterworth濾波器的傳遞函數系數以及歸一化截止頻率Wn”，且“截止頻率Wn必須滿足0.0 < Wn < 1.0，1.0對應于采樣率的一半。”

濾波器系數存儲在 Bd 和 Ad 變量中。

數字濾波器術語 – dspGuru by by Iowegian International

濾波器系數 – 與數字濾波器結構內的延遲信號采樣值相乘的常數集。數字濾波器設計就是要確定產生所需濾波器頻率響應的濾波器系數。對于FIR濾波器，根據定義，濾波器系數就是濾波器的脈沖響應。

濾波器階數 – 上述每種濾波器都有一個階數（N）特征；N階是指實現濾波器所需無功元件的數量。對于IIR濾波器，濾波器階數等于濾波器結構中的延遲元件數。通常，濾波器階數越大，濾波器的頻率幅度響應性能越好。

此濾波器的另一個重要方面是頻率響應——濾波器如何影響頻譜分量。濾波器的理想頻率響應應該是一個完整的矩形，其幅度為1，截止頻率為0.5。在現實生活中，您可以根據自己的應用場景選擇濾波器類型。

一個數字濾波器的頻率響應如下圖所示。在我們的例子中，通帶的幅度平坦，沒有紋波。截止頻率為3400Hz，這意味著我們的信號通過了一個低通濾波器，其頻率不會超過此限值。如圖所示，截止頻率后面沒有阻帶，這就是為什么可能有其他頻率比它高的原因。這可以通過增加濾波器的階數來改善。

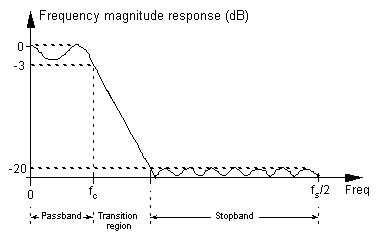
圖 9: 濾波器的頻率響應

如圖10所示，橢圓濾波器在截止頻率處的幅頻曲線下降最陡，但振幅不穩定。切比雪夫1和2在通帶和阻帶中有幅度波動。Butterworth濾波器在這兩個頻段上都沒有幅度波動，因此我們在應用中采用了這種濾波器；然而，這種濾波器的缺點是其過渡帶較大。

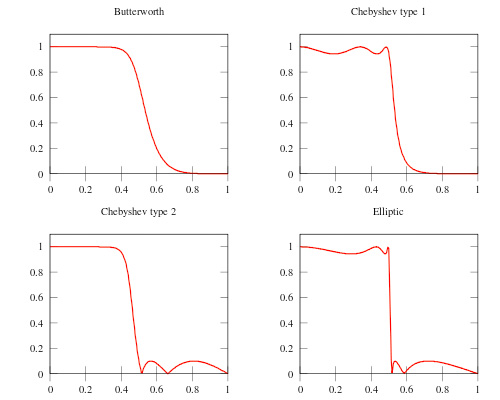
圖 10: IIR 濾波器類型

IIR濾波器的階數小于FIR濾波器的階數。

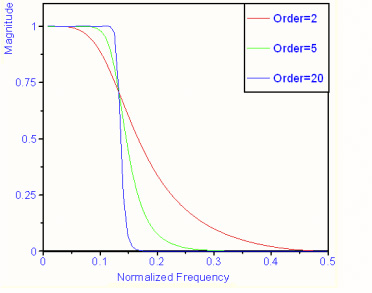
圖 11: 不同階數的Butterworth濾波器

在本文應用中，我們將濾波器的階數設為40，以使頻率響應盡可能地接近理想頻率響應。如圖11所示，隨著濾波器階數的增加，性能在頻率響應方面也會提高。

對信號進行濾波和抽取之后，我們需要觀察原始信號與變換信號之間的差異。我們使用繪圖功能并生成一個音頻信號。

驗證結果是否有效的最簡單方法就是查看這些信號。我們來比較一下原始信號（48kHz采樣率）和最終信號（16kHz采樣率）。最終信號沒有太大的噪音，這是一件非常好的事情。

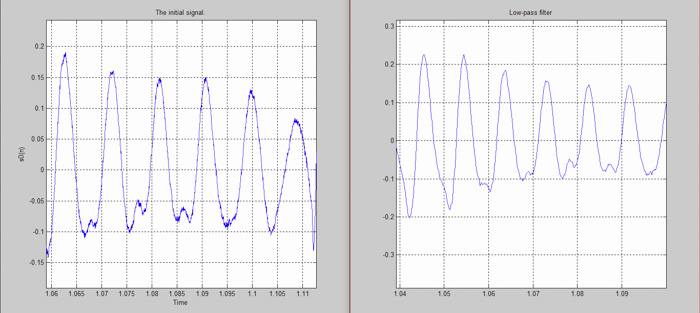
圖 12: 原始信號與經過濾波的信號之間的差異

在第2部分中，我們的目標是學習數字濾波器的特性并用MATLAB進行測試。到目前為止，我們已經設法了解了采樣率的含義以及采樣率的變化如何影響音頻信號。在下一篇文章中，我們將從另一個角度——利用傅里葉變換（即頻域）——處理音頻信號。

審核編輯：湯梓紅