傳遞函數的頻率特性
這里通過“傳遞函數的頻率特性”來考慮傳遞函數。和前項的“基爾霍夫定律和阻抗”中的解說有密切的關系所以希望合在一起閱讀。
首先,請看圖6。電阻和電容器組成簡單的閉合電路。首先,嘗試計算出本電路的傳遞函數。
為了讓電路圖容易形象化,將圖6改畫成圖7。當然,作為電路是相同的。這樣一來,能立刻明白ΔVout是ΔVin通過R和C的阻抗分割的。
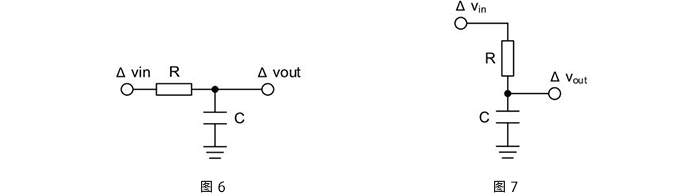
形成公式ΔVout = ΔVin ×(C/(R+C)),表示阻抗。?
正如前項的“基爾霍夫定律和阻抗”說明的那樣,雖然R的表示為R,

然后嘗試畫波特圖。波特圖是指橫軸為頻率(?),縱軸為增益(Gain)和相位(Phase)的圖表,需要計算按增益和相位。首先,從增益開始計算。
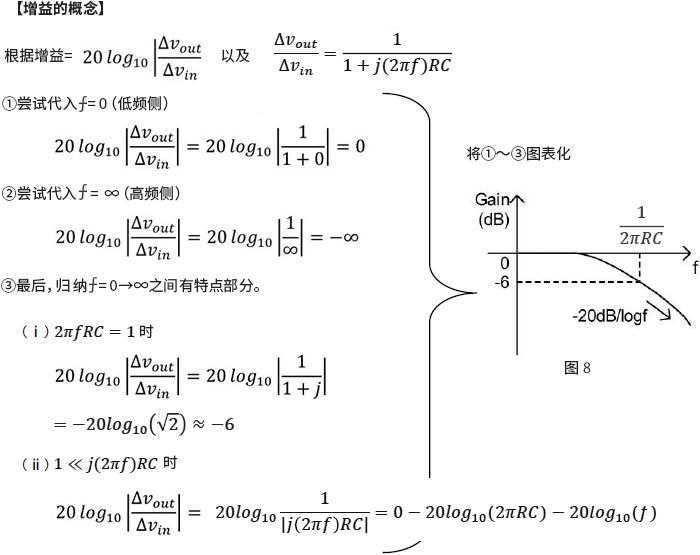
接著,計算相位。
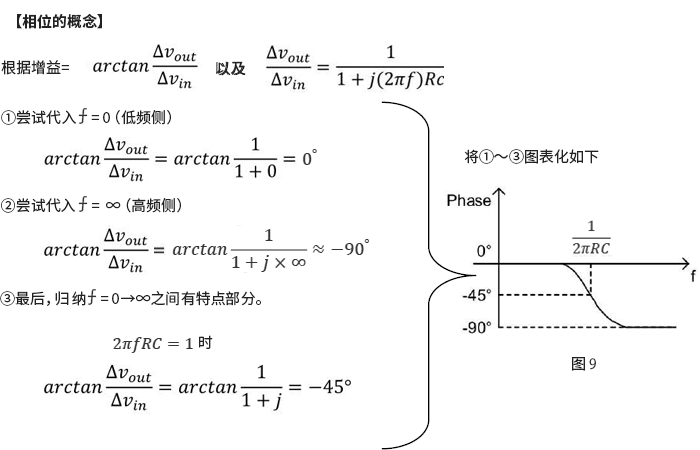
總結上述,如下面的圖10所示。至此,可以讓增益(Gain)和相位(Phase)的特性形象化。
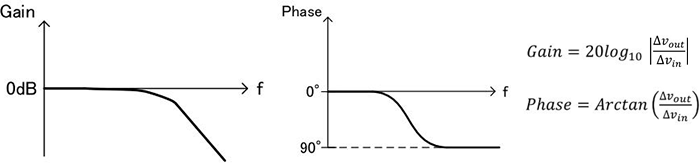
圖10
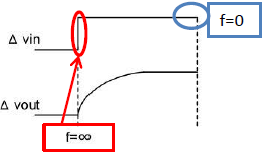
圖11
前項“基爾霍夫定律和阻抗”中,講述了電容器的阻抗表示為“1/jωC”,以達到理解傳遞函數的目的。請看圖11。
圖11是指圖6的電路的步進響應特性。電容器電源波動的瞬間(與f = ∞等值),電容器的阻抗為0,ΔVout=0。經過一定時間變為(與f=∞等值)ΔVin相等。
接著,圖形化如下。這是電容器步進響應針對阻抗“1/jωC”的示意圖。

圖12
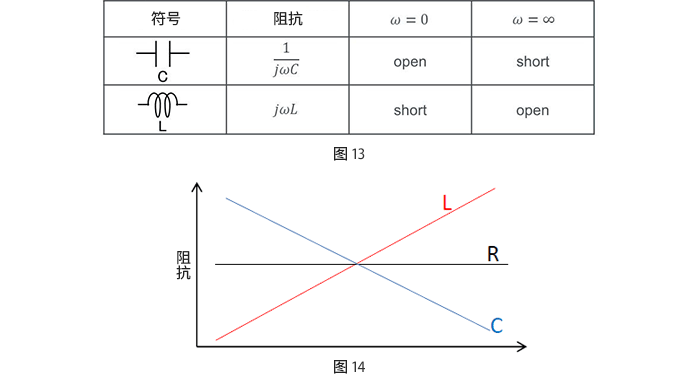
圖13中包括線圈的各元件的阻抗記述和ω=0以及ω=∞時的等價處理,而且,圖14中表示頻率特性。
審核編輯:湯梓紅
-
電容器
+關注
關注
64文章
6202瀏覽量
99311 -
傳遞函數
+關注
關注
0文章
102瀏覽量
13928 -
頻率特性
+關注
關注
0文章
39瀏覽量
9986
發布評論請先 登錄
相關推薦
濾波器的基礎知識
傳遞函數前言
二階系統動態特性的時頻虛擬測試
傳遞函數極點和零點的影響是什么
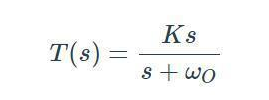




 傳遞函數的頻率特性
傳遞函數的頻率特性
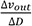










評論