了解抖動如何抑制諧波和非諧波雜散以及兩種不同類型的抖動系統:減法和非減法拓撲。
量化小幅度信號 可以在 量化誤差 和輸入,導致重要的諧波分量。高頻 諧波 可以混疊回奈奎斯特間隔的頻率,該頻率可能是也可能不是輸入的諧波。
在本文中,我們將看到抖動可以抑制諧波和非諧波雜散。我們還將介紹兩種不同類型的抖動系統,即減法和非減法拓撲,并了解每種類型的重要功能。
量化小信號時的高頻諧波
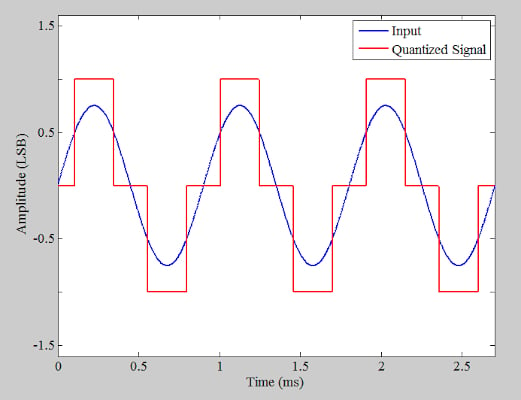
之前,我們討論過即使是理想的 模數轉換器 (ADC) 在數字化低振幅信號時產生諧波分量。例如,通過量化幅度為 0.75 LSB (最低有效位),我們在圖1的時域中得到以下波形。
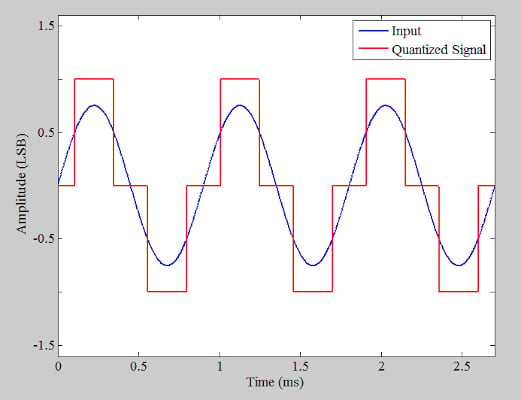
圖1.顯示輸入和量化信號的圖。
在4 MHz處對量化信號(上面的紅色曲線)進行采樣,并取其FFT(快速傅里葉變換),我們得到下面的頻譜(圖2僅顯示DC至200 kHz范圍)。
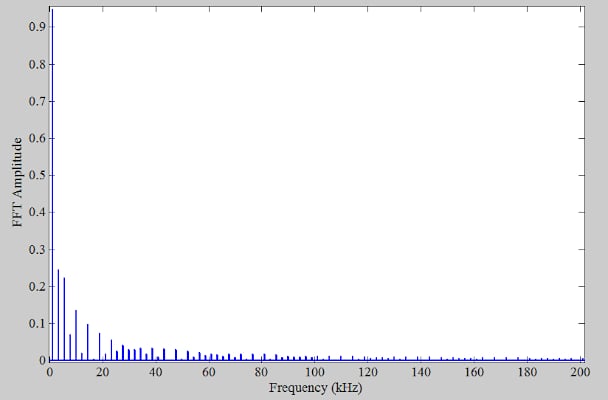
圖2. f的輸出頻譜s= 4 兆赫。
如本文第一部分所述,輸出頻譜中的諧波是量化操作的偽影。通過目視檢查,我們觀察到這些諧波在高達180 kHz的頻率下很容易辨別。為了產生上述曲線,我們故意使用遠高于 奈奎斯特采樣定理.這種高采樣頻率使我們能夠獲得信號的真實頻譜,而不受有限采樣頻率的影響(就好像信號是未采樣的模擬信號一樣)。
量化低振幅信號引起的混疊效應
如果我們使用較低的采樣率(例如40 kHz)來獲取輸出樣本會怎樣?根據奈奎斯特采樣準則,40 kHz足以成功采樣和重建1.11 kHz正弦波。然而,類似方波的信號具有高達40 kHz和超過40 kHz的顯著諧波分量。例如,33次和35次諧波(36.63 kHz和38.85 kHz)略低于我們的新采樣頻率fs= 40 kHz(圖 3)。
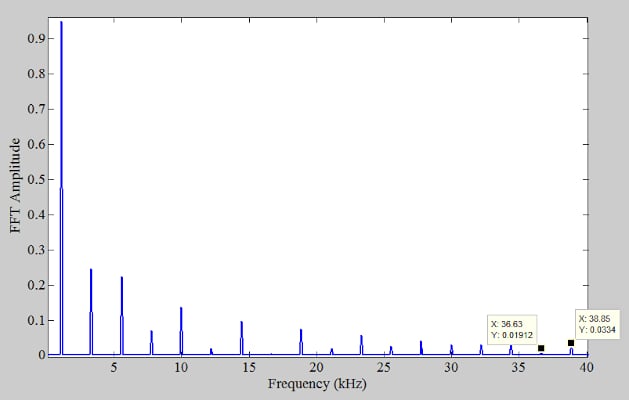
圖3. f的放大光譜s= 4 兆赫。
考慮到上述頻譜,40 kHz的采樣頻率實際上并不滿足奈奎斯特的采樣條件。因此,通過以40 kHz采樣,所有高于20 kHz的諧波都將混疊回奈奎斯特間隔,其頻率可能是也可能不是輸入的諧波。圖4顯示了采樣頻率為40 kHz時的輸出頻譜。
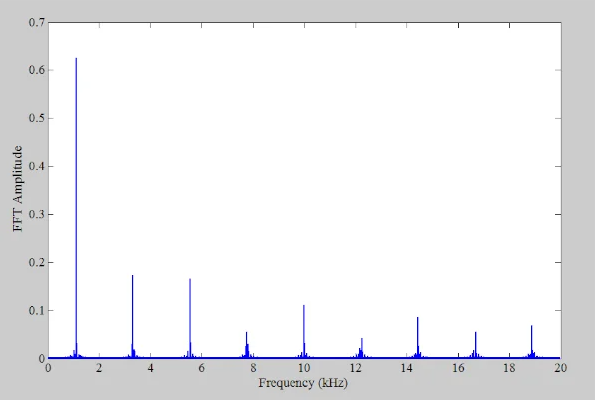
圖4. f的輸出頻譜s= 40 kHz。
上述頻譜中有諧波和非諧波分量。從圖3可以看出,當使用40 kHz采樣頻率時,我們預計36.63 kHz和38.85 kHz的分量將分別混疊回3.37 kHz和1.15 kHz。這些混疊分量如圖5所示,它提供了圍繞目標頻率的輸出頻譜的放大版本。
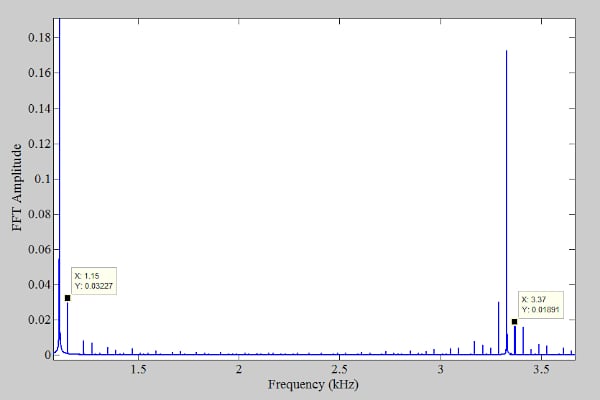
圖5.圍繞感興趣頻率的輸出頻譜的放大版本。
在信號中添加抖動噪聲可以破壞量化誤差和輸入之間的相關性,從而消除量化失真。因此,當使用40 kHz采樣頻率和抖動時,我們預計諧波和非諧波分量將消失。為了驗證這一點,我們添加了 噪聲 在量化之前對輸入進行三角形分布,然后以 40 kHz 進行采樣。三角形抖動 PDF(概率密度函數)的寬度取為 2 LSB。在這種情況下,獲得以下輸出頻譜(圖6)。
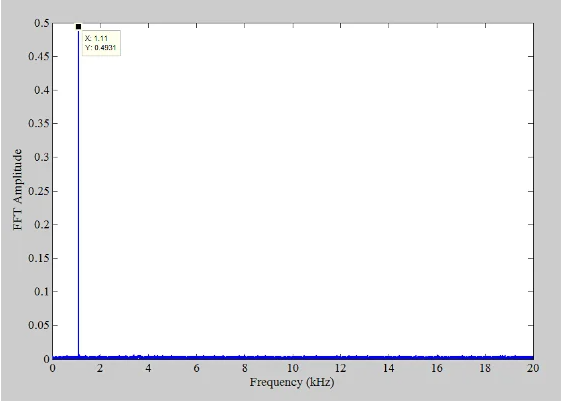
圖6.f的抖動系統的譜s= 40 kHz。
施加抖動時,輸入頻率處只有一個顯性分量。現在我們已經熟悉了抖動的功能,讓我們來看看應用這種技術的不同方法。
抖動方法:減法和非減法抖動
這兩種抖動方法如圖 7 所示。
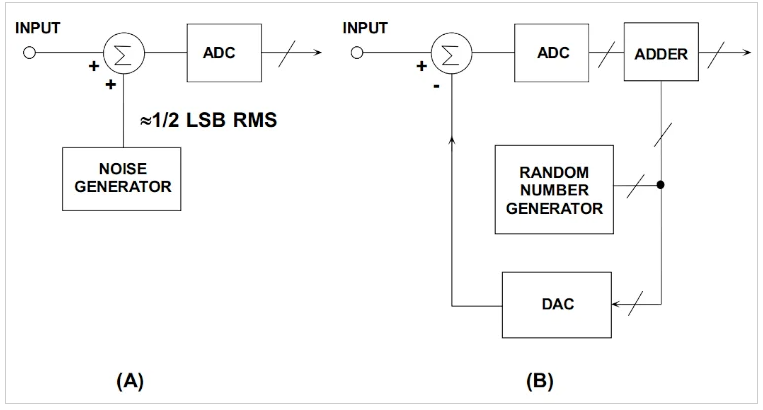
圖7.(a) 非減法和 (b) 減法抖動拓撲的簡單細分。圖片由 ADI公司
在減法(圖7(b))中,引入輸入端的噪聲以相反的極性添加到輸出端,從而將系統輸出端的凈抖動噪聲歸零。通過圖7(b)所示的特定實現,噪聲發生器的輸出被轉換為模擬值并從輸入中減去,而噪聲的數字等效值則通過加法器添加到輸出中。在非減法中,噪聲被引入輸入,而不從輸出中減去。
正如我們稍后將討論的那樣,減法抖動可能比非減法版本更強大,尤其是在處理量化失真時。然而,在許多實際情況下,不可能僅僅因為抖動噪聲在數字域中是未知的,就不可能從輸出中減去抖動信號。
減法抖動 — 消除量化失真
抖動背后的理論相對復雜且需要數學密集型。在這里,在不通過數學細節的情況下,我們將看一下一些結果。如前所述,我們應該記住,減法抖動比非減法方法更強大。對于任意輸入信號,可以證明具有適當抖動噪聲的減法系統可以呈現白色的量化誤差,在統計上與系統輸入無關,并且在(-frac{LSB}{2})到(+frac{LSB}{2})范圍內具有均勻分布。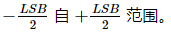
使量化噪聲具有這些所需特征的一個抖動信號是白噪聲,其均勻分布在(-frac{LSB}{2})到(+frac{LSB}{2})范圍內。
非減法抖動 — 減少量化失真
對于任意輸入,非減法拓撲不能使總誤差均勻分布或在統計上獨立于輸入。然而,一個設計得當的非減法系統仍然可以大大改善量化系統。我們在本文第一部分中提供的仿真結果對應于非減法系統。這些模擬證實了非減材系統的有效性。
在正確選擇抖動信號的情況下,非減法拓撲的總誤差功率P錯誤,總計可以通過公式1表示(有關更多詳細信息,請參閱上一節中提到的書)。
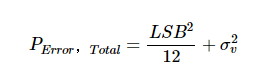
等式 1.
上述等式中的第一個項是眾所周知的 理想量化器的噪聲功率.第二項是抖動噪聲的方差。公式1直觀地有意義,因為它表明抖動噪聲功率與量化噪聲功率相加,從而決定了整個系統的本底噪聲。如果我們使用方差較大的抖動噪聲,則輸出噪聲水平會增加。換句話說,通過將抖動噪聲添加到輸入中,我們試圖打破量化噪聲和輸入之間的相關性,但代價是略微提高了本底噪聲。
常見抖動信號
抖動信號的一個重要特征是其概率密度函數。具有高斯、矩形或三角形分布的抖動信號用于不同的應用。可用于減少非減法系統量化失真的矩形和三角形抖動信號如圖9所示。
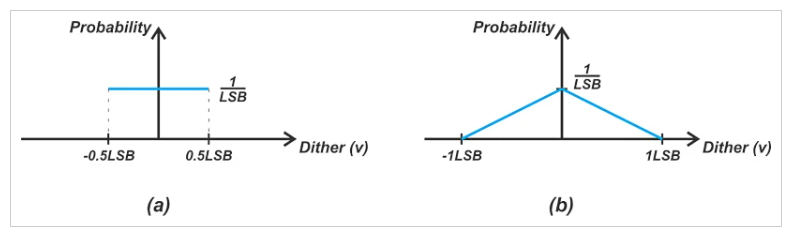
圖9.(a)矩形和(b)三角形抖動信號的圖,用于消除量化失真。
上述矩形和三角形抖動信號的方差分別為(frac{LSB^{2}}{12})和(frac{LSB^{2}}{6})。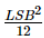 和
和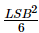 分別。
分別。
對于高斯抖動,建議的方差為 (frac{LSB^{2}}{4})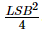 。
。
通過代入公式1中的這些值,我們可以計算出不同抖動類型的本底噪聲增加。與無抖動系統相比,應用矩形、三角形和高斯抖動可以使非減法系統的本底噪聲分別增加3 dB、4.8 dB和6 dB。
-
adc
+關注
關注
98文章
6452瀏覽量
544147 -
諧波
+關注
關注
7文章
812瀏覽量
41749 -
抖動
+關注
關注
1文章
69瀏覽量
18849 -
失真
+關注
關注
2文章
103瀏覽量
21326 -
模數轉換器
+關注
關注
26文章
3144瀏覽量
126747
發布評論請先 登錄
相關推薦
哪一個是減法器?負反饋在減法器電路中的原理?
減法運算
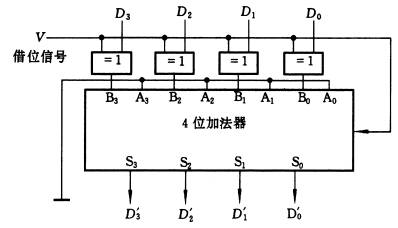
補碼減法,補碼減法原理是什么?
語義減法聚類研究
真空衰減法和壓力衰減法兩種方法的區別

壓力雙減法和無損真空衰減法的區別是什么?





 通過減法和非減法抖動減少量化失真
通過減法和非減法抖動減少量化失真











評論