一提到密度聚類,腦海中立馬就能呈現(xiàn)出一個聚類結(jié)果圖,不自然的就感覺非常的簡單,不就是基于密度的聚類嘛,原理不用看也懂了,但是真的實現(xiàn)起來,仿佛又不知道從哪里開始下手。這時候再仔細回想一下腦海中的密度聚類結(jié)果圖,好像和K-means聚類的結(jié)果圖是一樣的,那真實的密度聚類是什么樣子的呢?看了西瓜書的偽代碼后還是沒法實現(xiàn)?今天小編就帶大家解決一下密度聚類的難點。
實現(xiàn)一個神經(jīng)網(wǎng)絡,一定一定要先明白這個網(wǎng)絡的結(jié)構(gòu),**輸入是什么?輸出是什么?網(wǎng)絡的層級結(jié)構(gòu)是什么?權(quán)值是什么?每個節(jié)點代表的是什么?網(wǎng)絡的工作流程是什么?**
對于密度聚類,有兩個關(guān)鍵的要素,一個是密度的最小值,另一個是兩個樣本之間的最大距離。規(guī)定了密度最小值就規(guī)定了核心樣本鄰域包含數(shù)據(jù)的最小值,規(guī)定兩個樣本之間的最大距離就規(guī)定了兩個樣本相聚多遠才算是一類。而且,這兩個值都是需要不斷測試之后才選取的,并不是一次就那么容易定下來的。另一個需要了解的就是,密度聚類中有 **核心對象、密度直達、密度可達、和密度相連** ,這幾個概念。
核心對象就是指的一個類的核心,滿足兩個條密度聚類的關(guān)鍵要素,初始的核心對象有很多,但是經(jīng)過不斷迭代整合后,核心對象越來越少,到最后一個類形成后,核心對象就是一個抽象的概念,并不能明確的指出這個類的核心對象是哪一個,但一定是初始核心對象中的一個。初始的核心對象的鄰域中,一定包含多個核心對象。
用下圖來區(qū)分密度直達,密度可達和密度相連,假設X1為核心對象,那么X1和X2密度直達,X1和X3是密度可達,X3和X4是密度相連。密度相連就是兩個相聚比較遠的邊緣節(jié)點了,密度直達和密度可達距離都比較近。
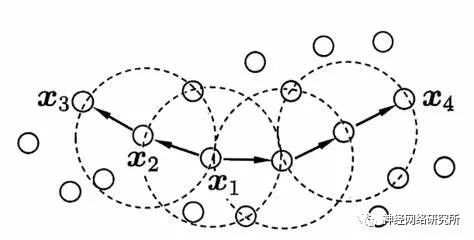
我們先理清一下密度聚類的過程:
- 首先要找到核心對象,即滿足周圍數(shù)據(jù)距離小于密度最小值的數(shù)據(jù)數(shù)量大于密度最小值,并且記錄下核心對象的鄰居節(jié)點。
- 隨機選取一個核心對象,找到對應的鄰居節(jié)點,即密度直達的節(jié)點,查看鄰居節(jié)點中包含的核心對象,將這幾個節(jié)點記錄下來,并在核心對象列表中刪除包含的核心對象,然后依次遍歷這幾個核心對象和它們的鄰居,按照相同的方法,記錄下的就是密度可達的節(jié)點。在遍歷開始時,添加一個判斷條件,判斷這個節(jié)點是不是滿足核心節(jié)點的條件,如果不滿足,那么就不再查找它的鄰域,這些節(jié)點就是密度相連節(jié)點,也就是這一個類的邊緣節(jié)點。
下面就是整個密度聚類的代碼:
#密度聚類
import numpy as np
import random
import time
import copy
np.set_printoptions(suppress=True)
def euclidean_distance(x, w): # 歐式距離公式√∑(xi﹣wi)2
return round(np.linalg.norm(np.subtract(x, w), axis=-1),8)
def find_neighbor(j, x, eps):
N = list()
for i in range(x.shape[0]):
temp = euclidean_distance(X[i],X[j]) # 計算歐式距離
print(str(j)+"到",str(i)+"的距離",'%.8f' % temp)
if temp <= eps:
N.append(i)
return set(N)
def DBSCAN(X, eps, min_Pts):
k = -1
neighbor_list = [] # 用來保存每個數(shù)據(jù)的鄰域
omega_list = [] # 核心對象集合
gama = set([x for x in range(len(X))]) # 初始時將所有點標記為未訪問
cluster = [-1 for _ in range(len(X))] # 聚類
for i in range(len(X)):
neighbor_list.append(find_neighbor(i, X, eps))
if len(neighbor_list[-1]) + int(count_matrix[i]) >= min_Pts: #如果權(quán)值對應位置的數(shù)據(jù)樣本數(shù)量和相似權(quán)值的數(shù)量之和大于一定的數(shù)
omega_list.append(i) # 將樣本加入核心對象集合
omega_list = set(omega_list) # 轉(zhuǎn)化為集合便于操作
while len(omega_list) > 0:
gama_old = copy.deepcopy(gama) #上一狀態(tài)未訪問的節(jié)點
j = random.choice(list(omega_list)) # 隨機選取一個核心對象
k = k + 1 #第幾個類別
Q = list()
Q.append(j) #選出來的核心對象
gama.remove(j) #標記為訪問過
while len(Q) > 0:#初始Q只有一個,但是后面會擴充
q = Q[0]
Q.remove(q) #把遍歷完的節(jié)點刪除
#正是下面這一個if決定了密度聚類的邊緣,不滿足if語句的就是密度相連,滿足就是密度直達或者密度可達
if len(neighbor_list[q]) >= min_Pts:#驗證是不是核心對象,找出密度直達
delta = neighbor_list[q] & gama #set的交集,鄰域中包含的未訪問過的數(shù)據(jù)
deltalist = list(delta)
for i in range(len(delta)):
Q.append(deltalist[i])#將沒訪問過的節(jié)點添加到隊列
gama = gama - delta #節(jié)點標記為訪問
Ck = gama_old - gama #記錄這一類中的節(jié)點
Cklist = list(Ck)
for i in range(len(Ck)):
cluster[Cklist[i]] = k #標記這一類的數(shù)據(jù)
omega_list = omega_list - Ck #刪除核心對象
return cluster
加載數(shù)據(jù)
X = np.load("文件位置")
X = X.reshape((-1,向量維度)) #修改維度
eps = 0.0000002 #兩個樣本之間的最大距離
min_Pts = 20 #樣本的最小值
C = DBSCAN(X, eps, min_Pts)
C = np.array(C)
np.save("classify.npy",C)
print("C",C.reshape([X原來的維度]))
注意一點,密度聚類的輸入數(shù)據(jù),不管是多少維,用這個代碼的話都要轉(zhuǎn)換成一維數(shù)據(jù)再進行密度聚類。舉個例子,二維數(shù)據(jù)row行,loc列,那么數(shù)據(jù)reshape成一維數(shù)據(jù)后,當前位置 i 對應的位置就是[(row*loc)+i]。如果有不懂或者有任何問題,歡迎留言討論!
-
核心
+關(guān)注
關(guān)注
0文章
44瀏覽量
15010 -
對象
+關(guān)注
關(guān)注
1文章
38瀏覽量
17340 -
密度聚類
+關(guān)注
關(guān)注
0文章
3瀏覽量
5734
發(fā)布評論請先 登錄
相關(guān)推薦
一種改進的基于密度聚類模糊支持向量機
基于DBSCAN的批量更新聚類算法
適用于公交站點聚類的DBSCAN改進算法
一種改進的基于密度聚類的入侵檢測算法
基于網(wǎng)格的多密度聚類算法
基于網(wǎng)格的快速搜尋密度峰值的聚類算法優(yōu)化研究
基于層次劃分的密度優(yōu)化聚類算法
基于密度差分的自動聚類算法
中點密度函數(shù)的模糊聚類算法
基于數(shù)據(jù)劃分和融合策略的并行DBSCAN算法
Python無監(jiān)督學習的幾種聚類算法包括K-Means聚類,分層聚類等詳細概述

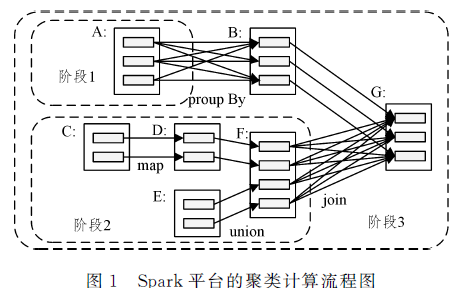
改進的DBSCAN聚類算法在Spark平臺上的應用




 代碼實現(xiàn)密度聚類DBSCAN
代碼實現(xiàn)密度聚類DBSCAN
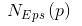










評論