3.1 概述
所謂模糊控制,就是對難以用已有規律描述的復雜系統,采用自然語言(如大,中,小)加以描述,借助定性的,不精確的以及模糊的條件語句來表達,模糊控制是一種基于語言的智能控制。
傳統的自動控制器的綜合設計都要建立在被控對象準確的數學模型(即傳遞函數模型或狀態空間模型)的基礎上,但是實際上,很多系統的影響因素很多,通常找出精確的數學模型,這種情況下,模糊控制的誕生就顯得意義重大,因為模糊控制不需要建立數學模型,不需要預先知道過程精確的數學模型。模糊控制與傳統的PID控制,具有如下優點:
(1)無需知道被控對象的數學模型
(2)反映人類智慧思維的智能控制
(3)易被人們所接受,是一種語言變量控制器
(4)構造容易,從屬于智能控制的范疇,尤其適用于非線性,時變,滯后系統的控制
(5)抗干擾能力強,響應速度快,并對系統參數的變化有較強的魯棒性
3.1.1 工作原理
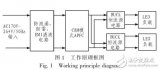
把各種傳感器測出的精確量轉換為適用于模糊運算的模糊量,然后將這些量在模糊控制器中加以運算,最后再將運算結果中的模糊量轉換為精確量,以便對各執行器進行具體的操作控制,這就說明在模糊控制中,存在著一個模糊量與精確量之間相互轉化的問題,如下圖所示:
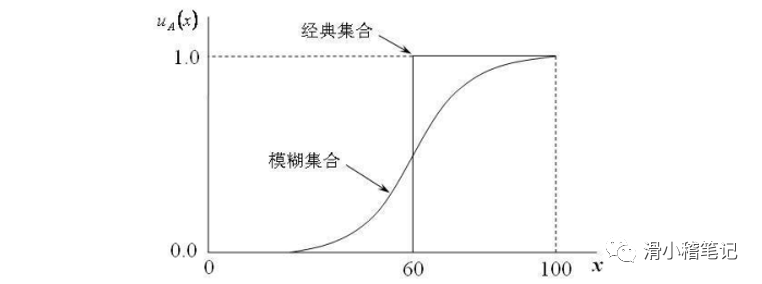
模糊控制原理圖如下圖所示:
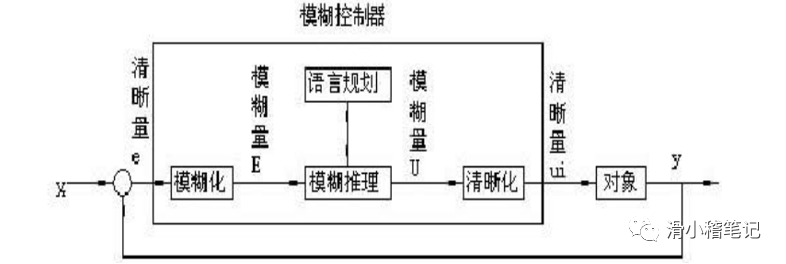
3.1.2 模糊語言集
模糊語言集用表示,一般有={負大,負中,負小,零,正小,正中,正大},用模糊語言變量E來描述偏差,或者用符號表示:
負大:Negative Big,簡稱NB
負中:Negative Medium,簡稱NM
負小:Negative Small,簡稱NS
零:Zero,簡稱ZE
正小:Positive Small,簡稱PS
正中:Positive Medium,簡稱PM
正大:Positive Big,簡稱PB

3.1.3 隸屬函數
各參數相對應子集的隸屬函數分別由不同的函數族決定,參數的相應子集指該參數被人為地劃分成的等級所構成的一組模糊集合,相應子集的多少,由控制精度決定,例如,參數“溫差”的相應子集可以是“正大,正中,負小,負大”,也可以是“正大,正中,正小,負小,負中,負大”,后者比前者模糊子集多,所以控制精度更高(在其他相同條件的情況下)。
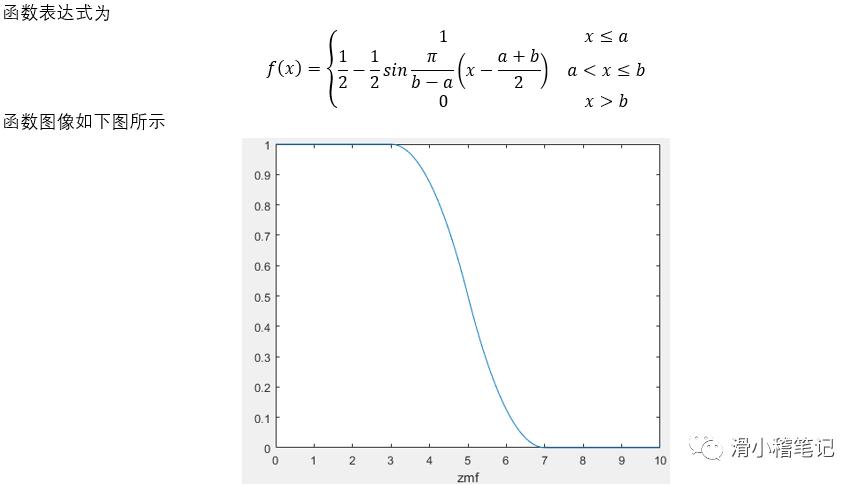
常用的隸屬函數如下所示。
(1)z型隸屬度函數zmf
(2)S型隸屬度函數smf
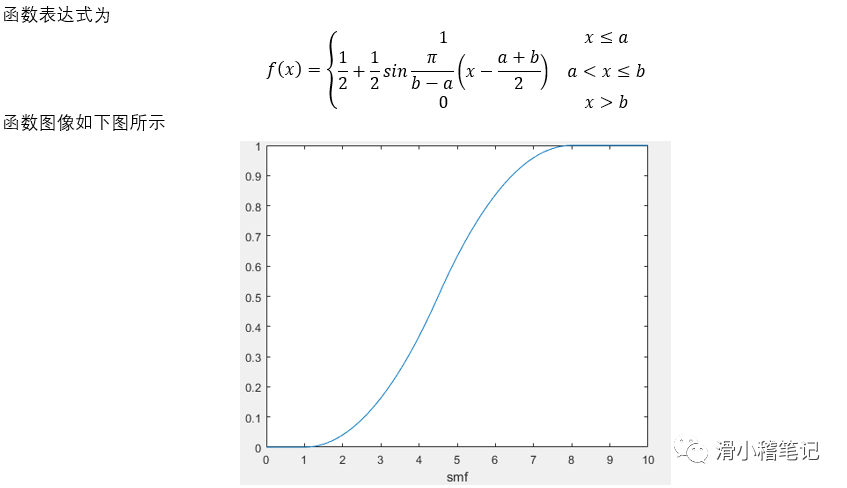
(3)三角形隸屬度函數trimf
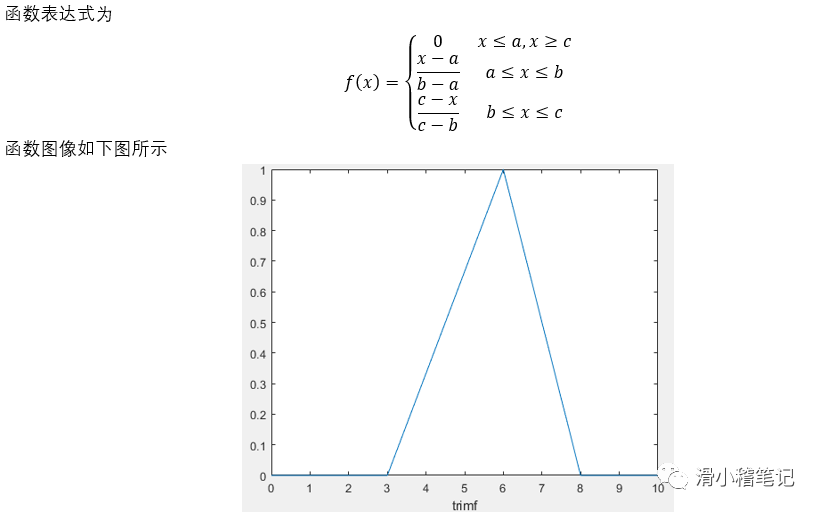
**3.2 **模糊控制數學基礎
3.2.1 模糊控制集合的代數運算

3.2.2 模糊關系
(1)普通關系:兩個集合中的元素之間是否有關聯。
(2)模糊關系:兩個模糊集合中的元素之間關聯程度的多少。

3.2.3 模糊關系的合成

3.2.4 模糊推理

3.2.5 模糊決策
模糊決策(模糊判決,解模糊,清晰化):由模糊推理得到的結論或者操作是一個模糊向量,轉化為確定值的過程。
(1)最大隸屬度法

(2)加權平均判決法

(3)中位數法

3.1.6 模糊推理的運用

3.2.7 模糊控制系統的組成

與一般的計算機控制系統不同的是,模糊控制系統的控制器是模糊控制器,模糊控制器是基于模糊條件語句描述的語言控制規則,又稱為模糊語言控制器。
輸入輸出變量
(1)模糊控制的輸入變量通常取E或E,EC或E,EC,ER,分別構成所謂的一維,二維,三維模糊控制器,一般選擇控制量的增量作為模糊控制器的輸出變量。
(2)描述模糊控制器的輸入,輸出變量狀態:負大(NB),負中(NM),負小(NS),零(O),正小(PS),正中(PM),正大(PB)。
(3)描述誤差變量的詞集一般取為:負大(NB),負中(NM),負小(NS),負零(NO),正零(PO),正小(PS),正中(PM),正大(PB)。
模糊變量E的賦值表
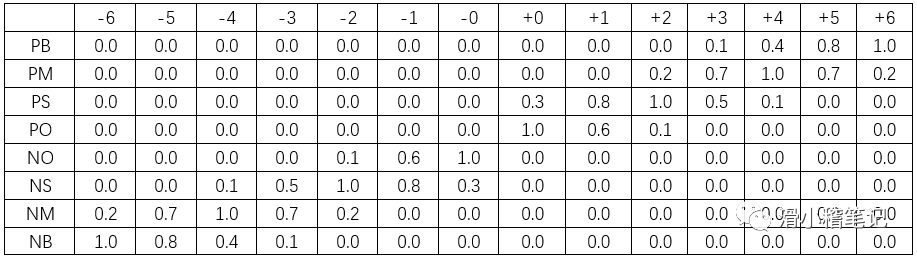
模糊控制規則
(1)條件語句的基本類型為:if A or B and C or D then E
例如水溫控制規則之一為:若水溫高或偏高,且溫度上升快或較快,則加大冷水流量。
用條件語句表達為:if E=NB or NM and EC=NB or NM then U=PB
3.2.8 模糊控制算法的工程實現
在大型的模糊控制系統中常采用軟件模糊推理法,模糊關系,模糊推理以及模糊判決的運算可以離線進行,最后得到模糊控制器輸入量的量化等級E,EC與輸出量即系統控制量的量化等級U之間的確定關系,這種關系通常稱為控制表。
3.3 水位控制系統
3.3.1 控制目標
控制模型如下圖所示,控制進水閥S1和出水閥S2,使水箱水位保持在目標水位O處。
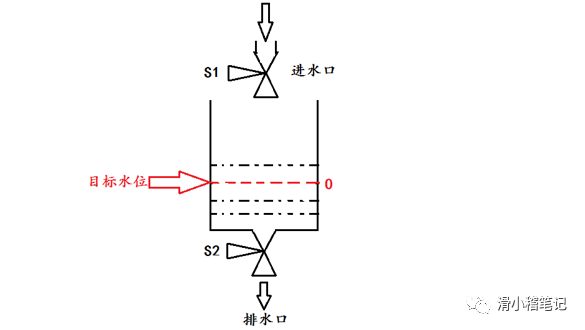
3.3.2 控制規則
(1)若當前水位高于目標水位,則向外排水,差值越大,排水越快
(2)若當前水位低于目標水位,則向內注水,差值越大,注水越快
(3)若當前水位和目標水位相差很小,則保持排水速度和注水速度相等
注:建立模糊控制規則的基本思想:當誤差大或較大時,選擇控制量應該以盡快消除誤差為主,而當誤差較小時,選擇控制量要防止超調,以系統的穩定性為主要出發點。
3.3.3 控制步驟
(1)我們選擇目標水位和當前水位的差值e作為觀察量,選取閥門開度u為控制量。
(2)將偏差e劃分為5個模糊集,負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB),e為負表示當前水位低于目標水位,e為正表示當前水位高于目標水位。設定e的取值范圍為[-3,3],隸屬度函數如下圖所示。
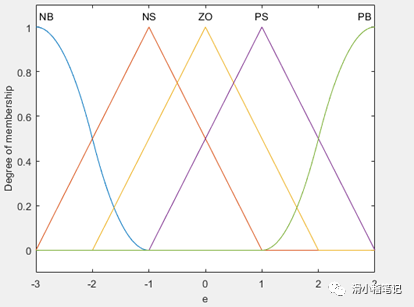
此時偏差e對應的模糊表如下表所示。
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
(3)將控制量u劃分為5個模糊集,負大(NB)、負小(NS)、零(ZO)、正小(PS)、正大(PB),u為負表示增大進水閥門S1的開度(同時減小出水閥門S2的開度),u為正表示減小進水閥門S1的開度(同時增大出水閥門S2的開度)。設定u的取值范圍為[-4,4],隸屬度函數如下。
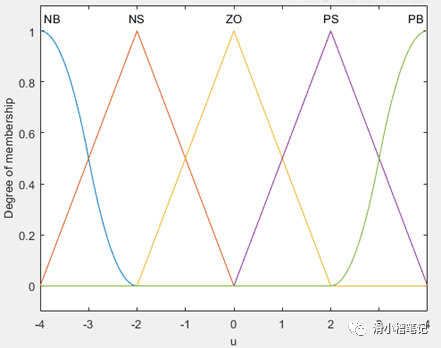
此時控制量u對應的模糊表如下表所示。
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|---|---|---|---|
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
| PS | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 |
| ZO | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 |
| NS | 0 | 0.5 | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| NB | 1 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
(4)制定模糊規則:模糊規則的制定是模糊控制的核心內容,控制性能的好壞很大程度上由模糊規則決定,目前主要是根據經驗來制定相應的規則
若e負大,則u負大
若e負小,則u負小
若e為零,則u為零
若e正小,則u正小
若e正大,則u正大
(6)進行模糊決策:最終需要的控制量u即為模糊控制的輸出,u可由偏差矩陣e和模糊關系矩陣R合成得到
(7)控制量的反模糊化
我們模糊決策得到的控制量u是一個矩陣,并不能直接應用在工程上,因此需要將u解釋為實際中的特定行為,即反模糊化操作。目前常用的反模糊化方法有以下幾種:
最大隸屬度法:應用于計算簡單控制要求不高場合
重心法:可以使得輸出更平滑
加權平均法:工業上應用最廣泛
3.4 模糊控制算法實現
3.4.1 MATLAB代碼
clc
clear
%創建模糊控制器
a = newfis('fuzzy tank');
%輸入變量
a = addvar(a,'input','e',[-3,3]); %設置變量e為輸入且定義域[-3,3]
a = addmf(a,'input',1,'NB','zmf',[-3,-1]); %Z型隸屬度函數
a =addmf(a,'input',1,'NS','trimf',[-3,-1,1]); %三角形隸屬度函數
a =addmf(a,'input',1,'ZO','trimf',[-2,0,2]); %三角形隸屬度函數
a =addmf(a,'input',1,'PS','trimf',[-1,1,3]); %三角形隸屬度函數
a = addmf(a,'input',1,'PB','smf',[1,3]); %S型隸屬度函數
%輸出變量
a = addvar(a,'output','u',[-4,4]); %設置變量u為輸出且定義域[-4,4]
a = addmf(a,'output',1,'NB','zmf',[-4,-2]); %Z型隸屬度函數
a =addmf(a,'output',1,'NS','trimf',[-4,-2,0]); %三角形隸屬度函數
a =addmf(a,'output',1,'ZO','trimf',[-2,0,2]); %三角形隸屬度函數
a =addmf(a,'output',1,'PS','trimf',[0,2,4]); %三角形隸屬度函數
a = addmf(a,'output',1,'PB','smf',[2,4]); %S型隸屬度函數
%建立模糊規則
rulelist=[1 1 1 1;
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];
a = addrule(a,rulelist);
%設置反模糊化算法
a1 = setfis(a,'DefuzzMethod','mom'); %采用最大隸屬度平均法進行反模糊化
writefis(a1,'tank'); %保存tank文件
a2 = readfis('tank'); %讀取tank文件
%繪制圖像
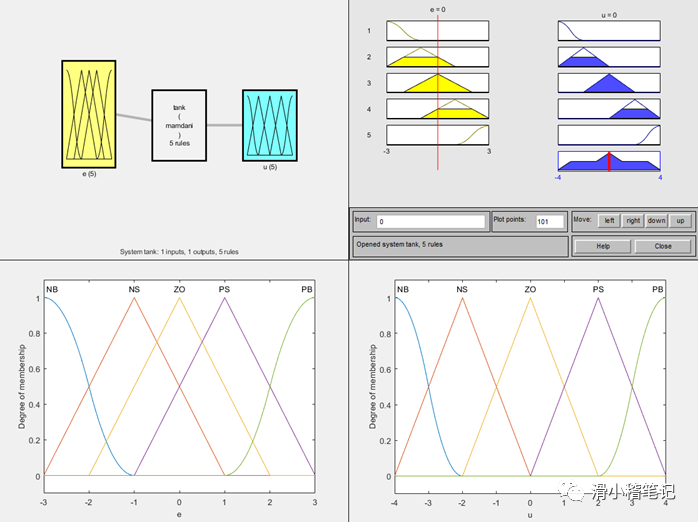
figure(1); plotfis(a2); %繪制模糊控制器結構
figure(2); plotmf(a,'input',1); %繪制輸入隸屬度函數圖像
figure(3); plotmf(a,'output',1); %繪制輸出隸屬度函數圖像
%打開模糊調試器
showrule(a);
ruleview('tank');
MATLAB仿真結果如下圖所示。
3.4.2 C語言代碼
#include
#include
#include
#define N 7 //定義量化論域模糊子集的個數
//模糊語言定義
#define NB -3
#define NM -2
#define NS -1
#define ZO 0
#define PS 1
#define PM 2
#define PB 3
struct
{
//規則表
int rule[ N ][ N ] ; //模糊規則表
//隸屬度函數
char *f_type_e ; //e的隸屬度函數類型
char *f_type_de ; //de的隸屬度函數類型
char *f_type_u ; //u的隸屬度函數類型
float paras_e[ 3*N ] ; //e的隸屬度函數的參數
float paras_de[ 3*N ] ; //de的隸屬度函數的參數
float paras_u[ 3*N ] ; //u的隸屬度函數的參數
//模糊運算參數
float Ke ; //Ke=n/emax,量化論域為[-3,-2,-1,0,1,2,3]
float Kde ; //Ke=n/demax,量化論域為[-3,-2,-1,0,1,2,3]
float Ku ; //Ke=umax/n,量¢化論域為[-3,-2,-1,0,1,2,3]
float umax ; //輸出的上限
float emax ; //誤差基本論域上限
float demax ; //誤差變化率基本論域的上限
//控制目標參數
float target ; //控制目標
float actual ; //實際值
float e ; //誤差
float e_pre ; //上一次的誤差
float de ; //誤差的變化率
}_fuzzy_;
/*******************************************************
Name :trimf
Function :三角隸屬度函數
Parameter :
x:自變量
(a,b,c):定義域
Return :結果
*******************************************************/
float trimf( float x, float a, float b, float c )
{
float u ;
if( ( x>=a )&&( x<=b ) )
u = ( x-a )/( b-a ) ;
else if( ( x>b )&&( x<=c ) )
u = ( c-x )/( c-b ) ;
else
u = 0 ;
return u ;
}
/*******************************************************
Name :gaussmf
Function :正態隸屬度函數
Parameter :
x:自變量
ave:均值
sigma:方差
Return :結果
*******************************************************/
float gaussmf( float x, float ave, float sigma )
{
float u ;
if( sigma<0 )
printf("方差不允許小于0\\n");
else
u = exp( -pow( ( ( x-ave )/sigma ), 2 ) ) ;
return u ;
}
/*******************************************************
Name :trapmf
Function :梯形隸屬度函數
Parameter :
x:自變量
(a,b,c,d):定義域
Return :結果
*******************************************************/
float trapmf( float x, float a, float b, float c, float d )
{
float u ;
if( ( x>=a )&&( xelse if( ( x>=b )&&( x
**
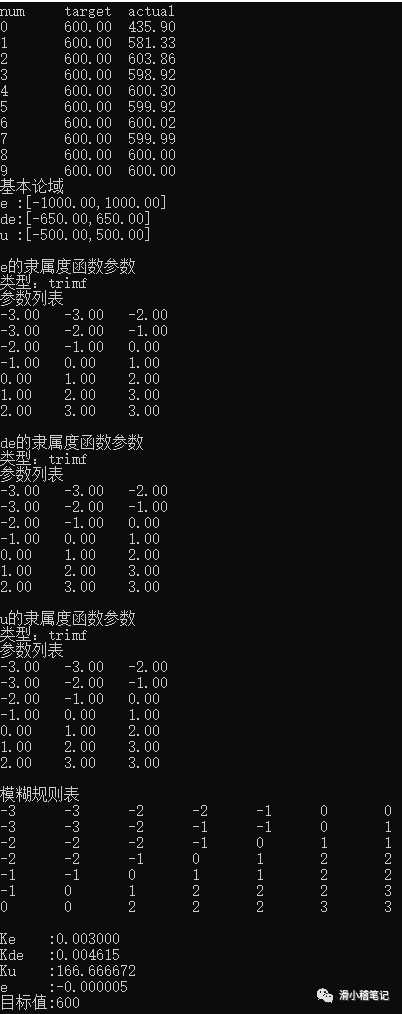
最終代碼運行結果如下圖所示。
參考于CDSN
**
-
模糊控制
+關注
關注
2文章
261瀏覽量
25487 -
復雜系統
+關注
關注
0文章
7瀏覽量
6983 -
自然語言
+關注
關注
1文章
287瀏覽量
13330
發布評論請先 登錄
相關推薦
PID算法之模糊PID 精選資料推薦
基于單片機模糊算法-PID
如何去實現一種基于單片機模糊算法溫度控制系統設計
基于模糊算法的水泥燒成控制系統研究
基于模糊算法的鍋爐經濟燃燒研究及應用
基于模糊算法的生化過程溫度控制系統
采用模糊算法的蘋果無損分揀技術研究
遺傳模糊算法在短期負荷預測中的應用
基于LO正則化去模糊算法
基于深度學習的圖像去模糊算法及應用
MATLAB學習筆記之模糊算法1
去模糊算法適對發射點擴散函數(PSF)的假設要求最低




 什么是模糊算法
什么是模糊算法










評論