當(dāng)電路頻率相同時(shí)，相量是分析交流電路中元件行為的有效方法。 兩個向量相加的結(jié)果取決于它們的相對相位，它們是“同相”還是“異相”，因?yàn)榇嬖谝恍┫辔徊睢?/p>

正弦波形是一種交變量，可以在時(shí)域中沿水平軸以圖形方式呈現(xiàn)。 作為時(shí)變量，正弦波形在時(shí)間 π/2 處具有正最大值，在時(shí)間3π/2處具有負(fù)最大值，零值沿基線出現(xiàn)在0、π和2π點(diǎn)。

然而，并不是所有的正弦波形都會同時(shí)準(zhǔn)確地通過零軸點(diǎn)，而是與另一個正弦波相比可能會向右或向左“偏移” 0 o某個值。

例如，將電壓波形與電流波形進(jìn)行比較。 然后這會在兩個正弦波形之間產(chǎn)生角度偏移或相位差。 在t = 0時(shí)不通過零的任何正弦波都具有相移。

正弦波形的差異或相移也稱為角度Φ（希臘字母 Phi），以度數(shù)或弧度表示波形從某個參考點(diǎn)沿水平零軸移動。 換句話說，相移是兩個或多個波形沿公共軸的橫向差異，相同頻率的正弦波形可以具有相位差。

相位之間的差異，交變波形的Φ可以在0到其最大時(shí)間周期之間變化，在一個完整的周期內(nèi)，波形的T可以在水平軸上的任何位置，Φ = 0 到 2π（弧度）或Φ = 0 到 360 o取決于所使用的角度單位。

相位差也可以表示為τ的時(shí)間偏移（以秒為單位，代表時(shí)間段的一部分），例如T，+10mS 或 – 50uS，但通常更常見的是將相位差表示為角度測量值。

然后我們在之前的正弦波中開發(fā)的正弦電壓或電流波形的瞬時(shí)值方程將需要修改以考慮波形的相位角，這個新的通用表達(dá)式變?yōu)椤?/p>

相位差方程

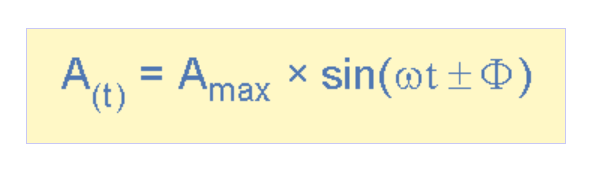
在哪里：

A m – 是波形的幅度。

ωt – 是以弧度/秒為單位的波形角頻率。

Φ (phi) – 是波形從參考點(diǎn)向左或向右移動的相位角，以度或弧度為單位。

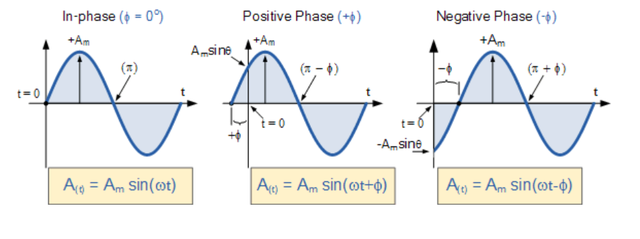
如果正弦波形的正斜率在t = 0 “之前”通過水平軸，則波形已向左移動，因此Φ > 0，并且相位角本質(zhì)上將為正，+Φ給出超前相位角。 換句話說，它出現(xiàn)的時(shí)間早于 0 o，產(chǎn)生矢量的逆時(shí)針旋轉(zhuǎn)。

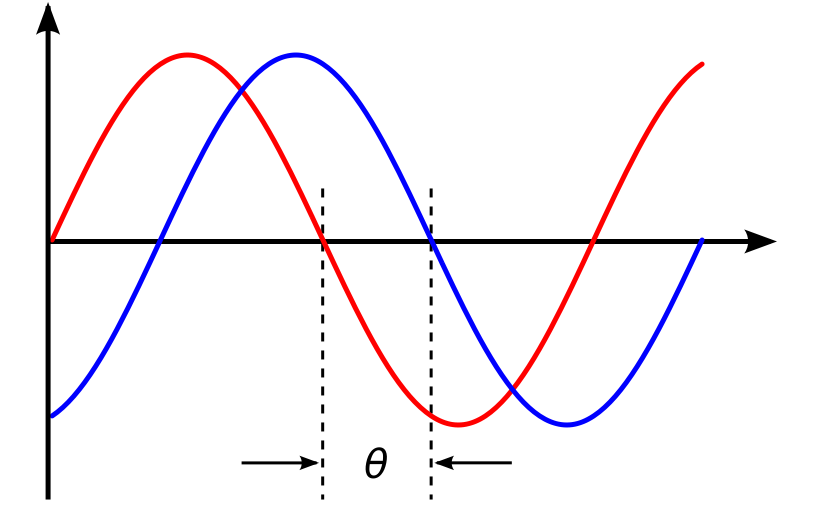
同樣，如果正弦波形的正斜率在t = 0 “之后”的某個時(shí)間通過水平 x 軸，則波形向右移動，因此Φ < 0，并且相位角本質(zhì)上將為負(fù)-Φ產(chǎn)生滯后的相位角，因?yàn)樗霈F(xiàn)的時(shí)間晚于 0 o，產(chǎn)生矢量的順時(shí)針旋轉(zhuǎn)。 兩種情況如下所示。

正弦波形的相位關(guān)系

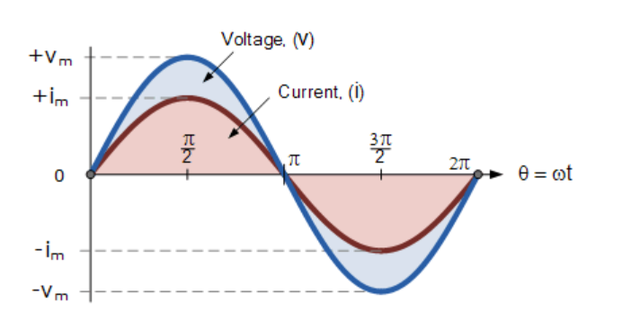
首先，讓我們考慮兩個交變量，例如電壓v和電流i具有相同的頻率?以赫茲為單位。 由于這兩個量的頻率與角速度相同，因此ω也必須相同。 所以在任何時(shí)刻我們都可以說電壓的相位v將與電流的相位相同i。

那么特定時(shí)間段內(nèi)的旋轉(zhuǎn)角度將始終相同，因此v和i兩個量之間的相位差將為零且Φ = 0。 由于電壓v和電流i的頻率相同，因此它們必須在一個完整的周期內(nèi)同時(shí)達(dá)到其最大正值、負(fù)值和零值（盡管它們的幅度可能不同）。 那么這兩個交變量v和i被稱為“同相”。

兩個正弦波形——“同相”

現(xiàn)在讓我們考慮電壓v和電流i之間有30 o的相位差 ，因此（Φ = 30 o或π /6弧度）。 由于兩個交變量以相同的速度旋轉(zhuǎn)，即它們具有相同的頻率，因此該相位差將在所有瞬間保持恒定，則 兩個量之間的30 °相位差由 phi 表示， Φ如下所示。

正弦波形的相位差

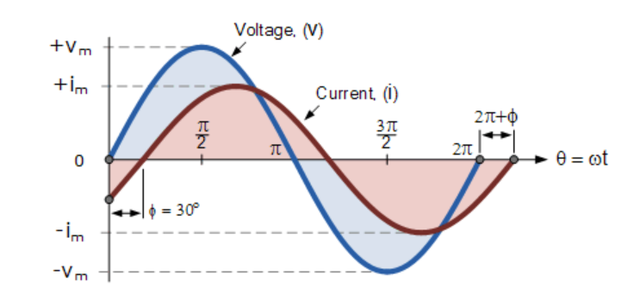
上面的電壓波形沿水平參考軸從零開始，但在同一時(shí)刻，電流波形的值仍然為負(fù)，并且直到30 o之后才穿過該參考軸。 然后當(dāng)電流穿過水平參考軸在電壓波形之后達(dá)到其最大峰值和零值時(shí)，兩個波形之間存在相位差。

由于兩個波形不再“同相”，因此它們必須“異相”，其大小由 phi, Φ決定，在我們的示例中為30 o。 所以我們可以說這兩個波形現(xiàn)在是30 o異相。 也可以說電流波形“滯后”于電壓波形相角Φ。 然后在我們上面的示例中，兩個波形具有滯后相位差，因此上面的電壓和電流的表達(dá)式將給出為。

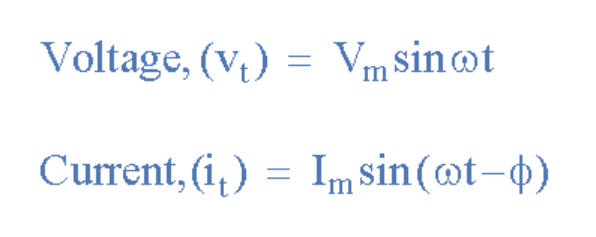
其中電流i “滯后”電壓v相位角Φ

同樣，如果電流i具有正值并穿過參考軸，在電壓v之前的某個時(shí)間達(dá)到其最大峰值和零值，則電流波形將“超前”電壓某個相位角。 然后這兩個波形被稱為具有超前相位差，電壓和電流的表達(dá)式都是。

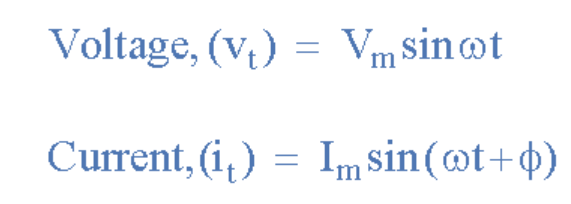
其中電流i “超前”電壓v相位角Φ

正弦波的相位角可用于描述一個正弦波與另一個正弦波的關(guān)系，使用術(shù)語“超前”和“滯后”來表示繪制在同一參考軸上的兩個相同頻率的正弦波形之間的關(guān)系. 在我們上面的示例中，兩個波形異相30 o。 所以我們可以正確地說i滯后v或者我們可以說v領(lǐng)先i 30 o，這取決于我們選擇哪個作為我們的參考。

可以沿水平零軸的任何位置測量兩個波形之間的關(guān)系和產(chǎn)生的相位角，每個波形以“相同斜率”方向通過，無論是正向還是負(fù)向。

在交流電源電路中，這種描述同一電路內(nèi)電壓和電流正弦波之間關(guān)系的能力非常重要，并且構(gòu)成了交流電路分析的基礎(chǔ)。

余弦波形

所以我們現(xiàn)在知道，如果與另一個正弦波相比，一個波形向0 o的右側(cè)或左側(cè)“移動”，則該波形的表達(dá)式變?yōu)锳 m sin(ωt ± Φ )。 但是，如果波形在參考波形之前以正向斜率90 o或π /2弧度穿過水平零軸，則該波形稱為余弦波形，表達(dá)式變?yōu)椤?/p>

余弦表達(dá)式

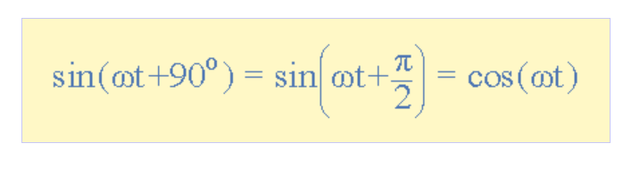
余弦波，簡稱“cos”，在電氣工程中與正弦波一樣重要。 余弦波與其對應(yīng)的正弦波具有相同的形狀，即它是一個正弦函數(shù)，但在它之前移動了+90 o或一個完整的四分之一周期。

正弦波和余弦波的區(qū)別

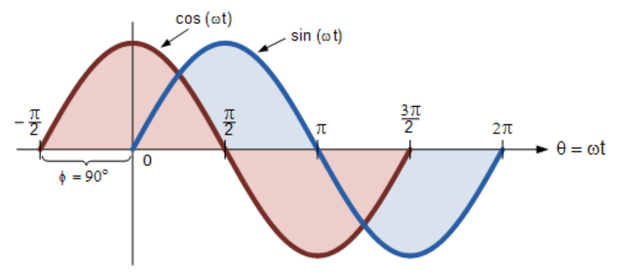
或者，我們也可以說正弦波是在另一個方向上偏移了-90 o的余弦波。 無論哪種方式，在處理具有角度的正弦波或余弦波時(shí)，始終適用以下規(guī)則。

正弦波和余弦波關(guān)系

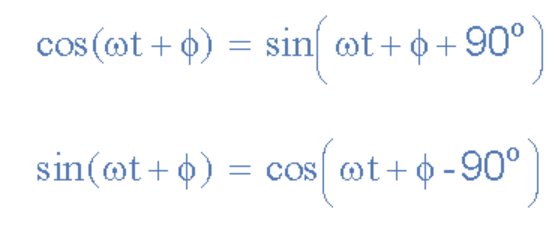
比較兩個正弦波形時(shí)，更常見的是將它們的關(guān)系表示為具有正向振幅的正弦或余弦，這是使用以下數(shù)學(xué)恒等式實(shí)現(xiàn)的。 通過使用上面的這些關(guān)系，我們可以將具有或不具有角度或相位差的任何正弦波形從正弦波轉(zhuǎn)換為余弦波，反之亦然。

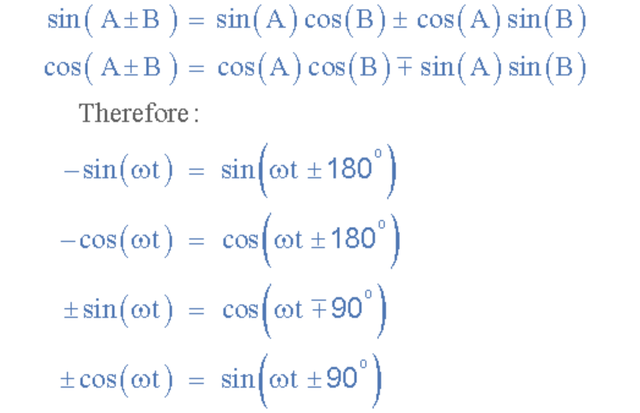
在下一個關(guān)于向量的教程中，我們將使用圖形方法來表示或比較兩個正弦波之間的相位差，方法是查看單相交流量的向量表示以及與兩個或多個向量的數(shù)學(xué)加法相關(guān)的一些向量代數(shù)。