1、非正弦周期信號

在實際中，通常會遇到按非正弦規(guī)律變化的信號，另外，如果電路存在非線性元件，即使在正弦信號的作用下也會產(chǎn)生非正弦周期的響應(yīng)。非正弦信號分為周期和非周期兩種。傅里葉變換主要用于研究周期信號的電路響應(yīng)。

2、信號分解為傅里葉級數(shù)

（1）信號分解為傅里葉級數(shù)的條件：若周期信號滿足狄里赫利條件，即函數(shù)具有有限個極值點或第一類間斷點，且函數(shù)在一個周期內(nèi)絕對可積，則信號就可以分解為傅里葉級數(shù)。傅里葉級數(shù)分為兩種形式，即三角函數(shù)形式和指數(shù)形式。

3、傅里葉變換的性質(zhì)

4、典型信號的傅里葉變換

注：以上是一些常用的傅里葉變換，其余的非典型信號的傅里葉變換可以根據(jù)傅里葉變換的性質(zhì)和基本信號的傅里葉變換公式推導(dǎo)得出，能不積分盡量不要積分。

6、傅里葉變換在電路中的應(yīng)用

利用傅里葉變換來分析電路的參數(shù)過程如下：

第一步：將輸入激勵分解為三角函數(shù)形式的傅里葉級數(shù)；

第二步：將電路中的R，L，C元件的阻抗形式寫出來，分析計算出各次諧波情況下的具體阻抗；

第三步：將各次諧波的結(jié)果疊加即可。

7、采樣定理

（1）采樣定理敘述：若一個信號被采樣后想要恢復(fù)成原信號，則采樣頻率必須大于等于信號頻率的2倍。

（2）常用信號形式的采樣頻率確定：對于和信號，其頻率應(yīng)該取和信號中的最高頻率；對于卷積信號，其頻率應(yīng)該取信號中最低頻率的信號；對于乘積信號，其頻率應(yīng)該取信號分量的頻率之和。

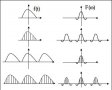
8、周期信號的頻譜

（1）三角函數(shù)形式的傅里葉級數(shù)的頻譜為單邊譜，分為單邊幅度譜和單邊相位譜，即將各個頻率的幅值和相位畫在一個直角坐標(biāo)系中。

（2）指數(shù)形式的傅里葉級數(shù)的頻譜為雙邊譜，分為雙邊幅度譜和雙邊相位譜，其中幅度譜關(guān)于幅值軸對稱，相位譜則關(guān)于原點對稱。

9、例題分析

例題2：求下列信號的傅里葉變換

例題3：求下列信號的傅里葉反變換