CORDIC算法簡介
在信號處理領域,CORDIC(Coordinate Rotation Digital Computer,坐標旋轉數字計算機)算法具有重大工程意義。CORDIC算法由Vloder于1959年在設計美國航空導航控制系統時提出,主要用于解決導航系統中三角函數、反三角函數和開方等運算的實時計算問題。
1971年,Walther將圓周系統、線性系統和雙曲線系統統一到一個CORDIC迭代方程里,從而額提出了一種統一的CORDIC算法形式。
CORDIC算法的核心是利用加法和移位的迭代操作去替代復雜的運算,從而非常有利于硬件實現。CORDIC算法應用廣泛,如離散傅里葉變換(DFT)、離散余弦變換(DCT)、離散Hartley變換、Chirp-Z變換、各種濾波以及矩陣中的奇異值分解。
在工程領域,可采用CORDIC算法實現直接數字頻率合成器(DDS)、計算I/Q信號的幅度和相位。
01
CORDIC基本原理
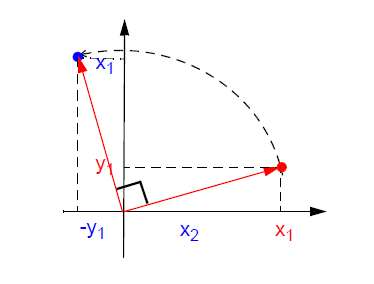
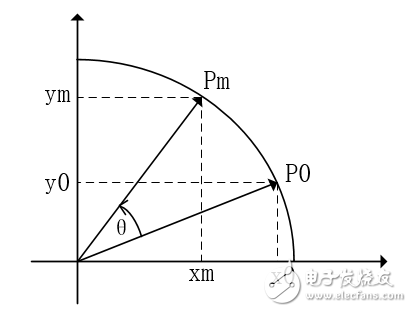
我們假設在笛卡爾坐標系(也就是我們常見的XY直角坐標系)中,將點(x1,y1)旋轉θ角度到點(x2,y2)的標準方法如下所示:
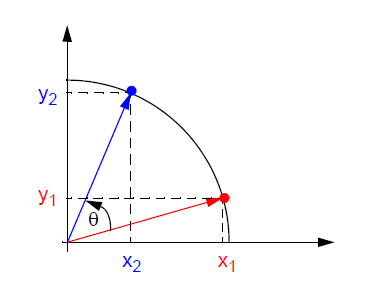
根據上圖,我們利用高中學習的三角函數、圓方程和極坐標等中學知識,可以得到:
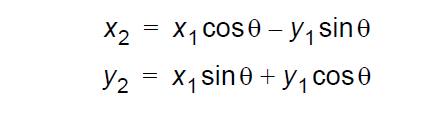
這被稱為是平面旋轉、向量旋轉或者線性 ( 矩陣) 代數中的 Givens 旋轉。
上面的式子,我們將大學二年級學習的線性代數知識拿出來,用矩陣的形式來表示,于是得到:
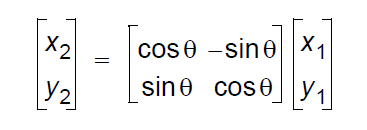
例如,我們做一個90°的相移,即θ=90:
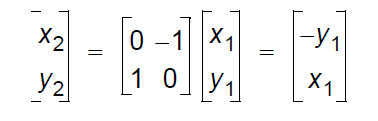
這里注意cos和sin函數在直角坐標系下的物理意義,于是我們得到下面的圖示。
上面的第一個式子,我們假設提出一個公因子cosθ,那么我們可以得到:
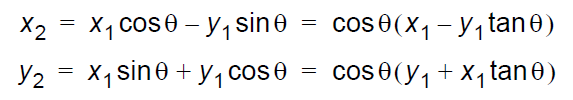
如果去除項,我們得到 偽旋轉 方程式 :
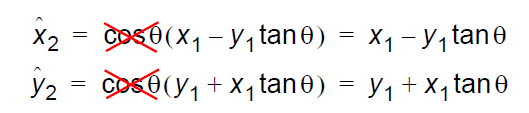
即旋轉的角度是正確的,但是x 與 y 的值增加cos-1θ 倍 ( 由于cos-1θ> 1),所以模值變大。
注意我們并不能通過適當的數學方法去除cosθ 項 , 然而隨后我們發現去除項可以簡化坐標平面旋轉的計算操作。
怎么說呢?
在XY坐標系中,結合上面的偽旋轉公式,我們可以用下圖表示:
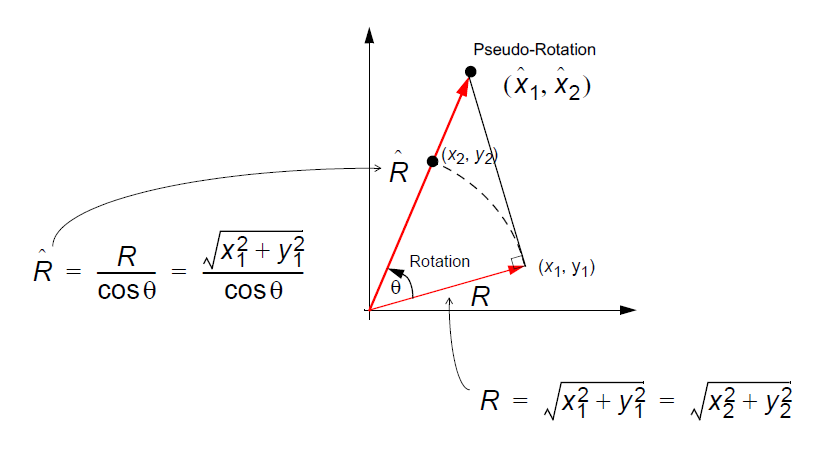
于是,我們得出以下結論:
經過偽旋轉之后,向量 R 的模值將增加1/cosθ 倍。
向量旋轉了正確的角度 , 但模值出現錯誤。
經過偽旋轉后, 輸出進行適當的幅度伸縮(1/cosθ),是不是就可以得到旋轉后的坐標了。
02
CORDIC方法
CORDIC 方法的核心是 ( 偽) 旋轉角θ,其中,
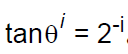
這個等式是怎么推導出來的呢?
所以方程為:
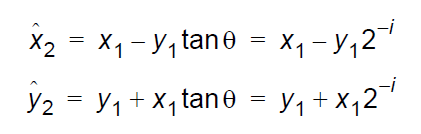
下面的表格指出用于 CORDIC 算法中每個迭代 (i) 的旋轉角度 (精確到 9位小數):
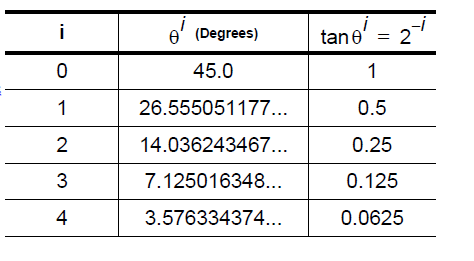
note:由于i是整數,所以對應的角度值都是一一確定的,只能通過幾個角度的加減組合來達到你所想要的角度值.
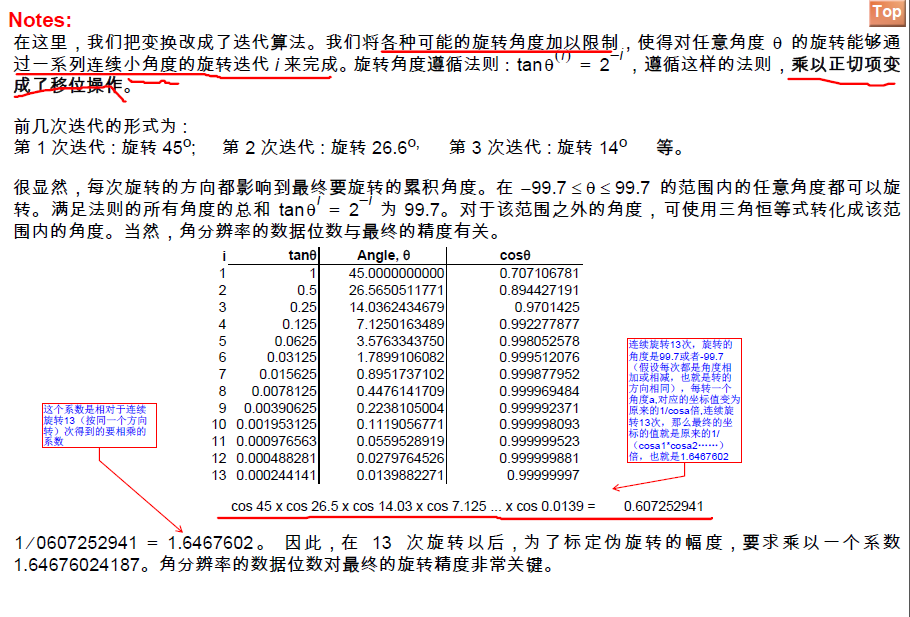
注意有三個方面的變化:
角度累加(減)
坐標值累加(減)
向量的模(也就是長度的,相對于橫縱坐標的)累加(減)
這三個累加的變化時不一樣的,注意區別,角度的累加和長度的累加有一定的對應關系。
03
角度累加器


上述三個方程式為圓周坐標系中用于角度旋轉的 CORDIC 算法的表達式。后續部分中我們還將看到CORDIC 算法被用于其它的坐標系,通過使用這些坐標系可以執行更大范圍的函數計算。
04
移位-加法算法
因此, 原始的算法現在已經被減化為使用向量的偽旋轉來表示的迭代移位-相加算法 :
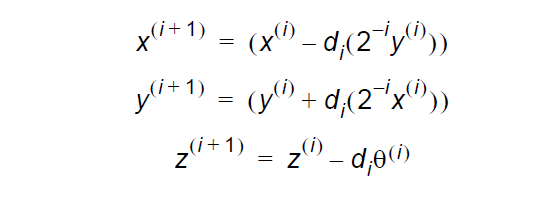
因此,每個迭代需要:

note:前面提到的去除 cos 項的原因是顯而易見的。當將該項去除時,轉換公式已經被簡化為偽旋轉的迭代移位相加計算。
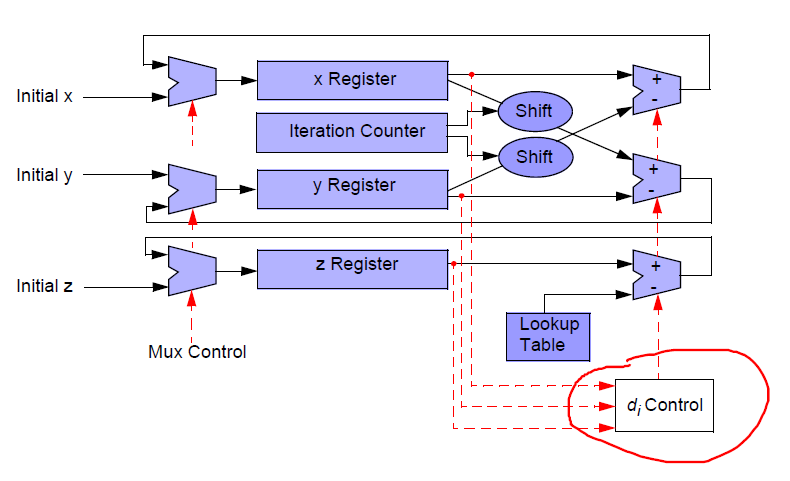
CORDIC 硬件實現結構:
05
伸縮因子
前面提到,為了得到偽旋轉公式,我們把公因子cosθ忽略了,但在實際運算中,不能就這樣簡單粗暴拋棄。
我們再次對cosθ進行變形:

于是,我們可以得到:

如果我們已知了將被執行的迭代次數,我們便可以預先計算出 1/Kn 的值,并通過將 1/Kn 與 x(n) 和 y(n)相乘來校正x(n) 和 y(n) 的最終值。
CORDIC有兩種工作模式:旋轉模式和向量模式。

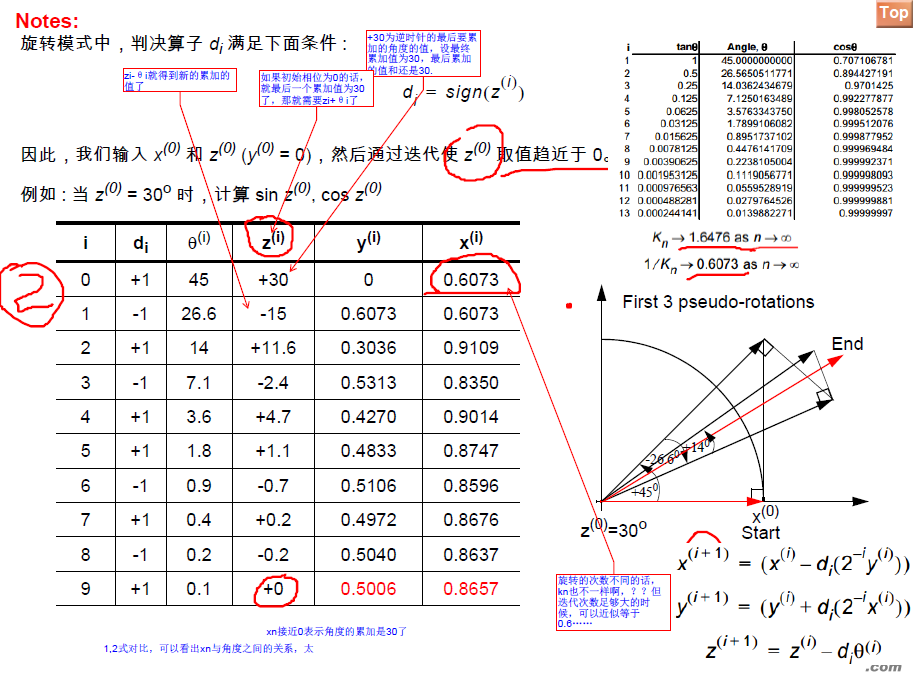

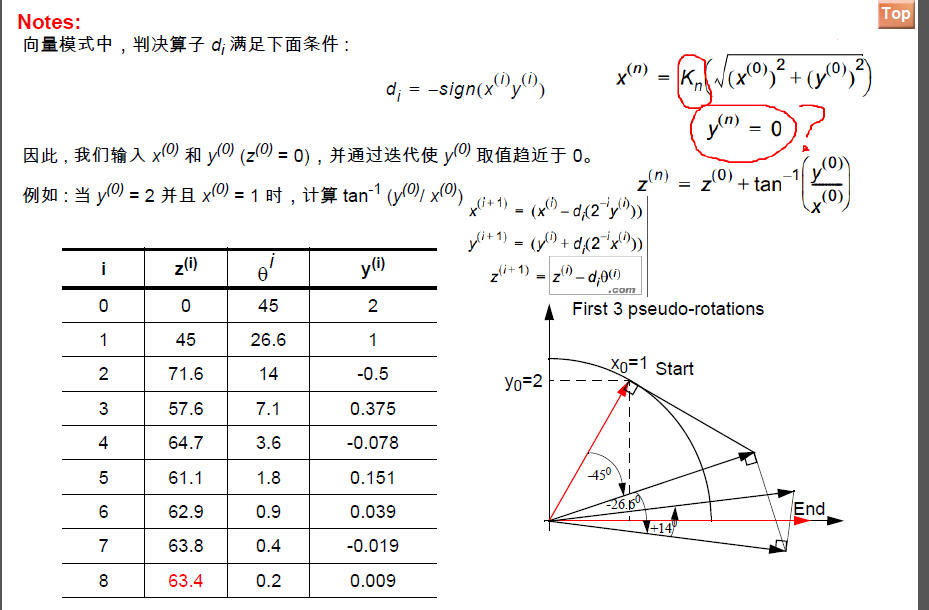
06
三種坐標系下的CORDIC
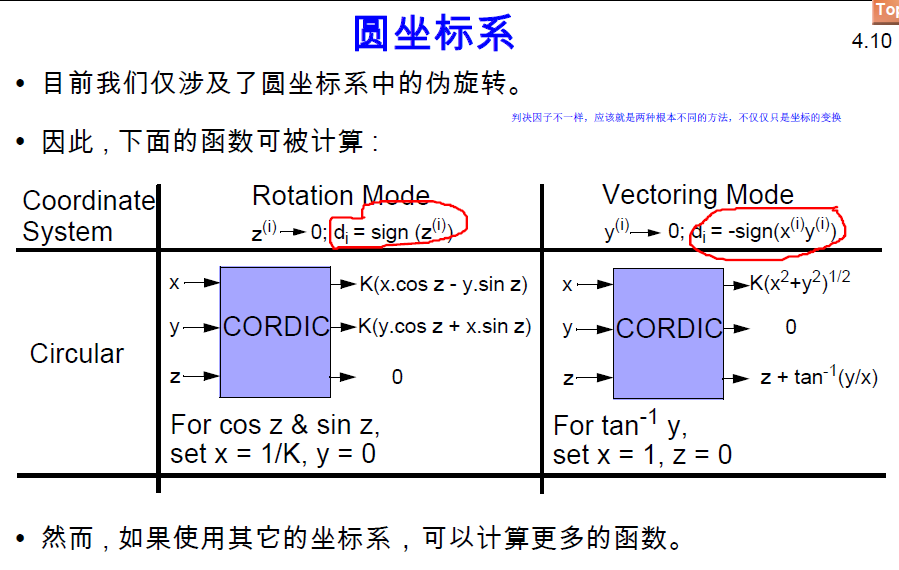
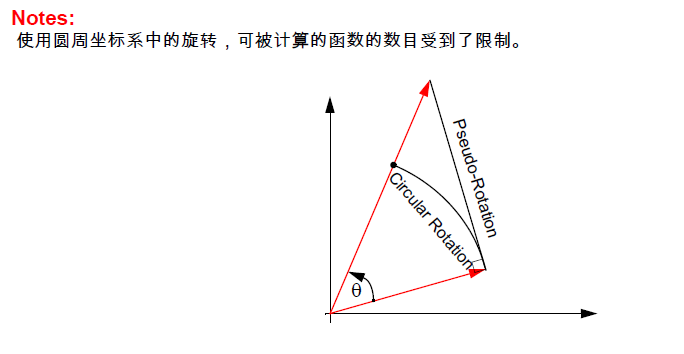
然而, 我們將會看到,通過考慮其它坐標系中的旋轉, 我們可以直接計算更多的函數, 如乘法和除法, 進而間接計算更多的其它函數。
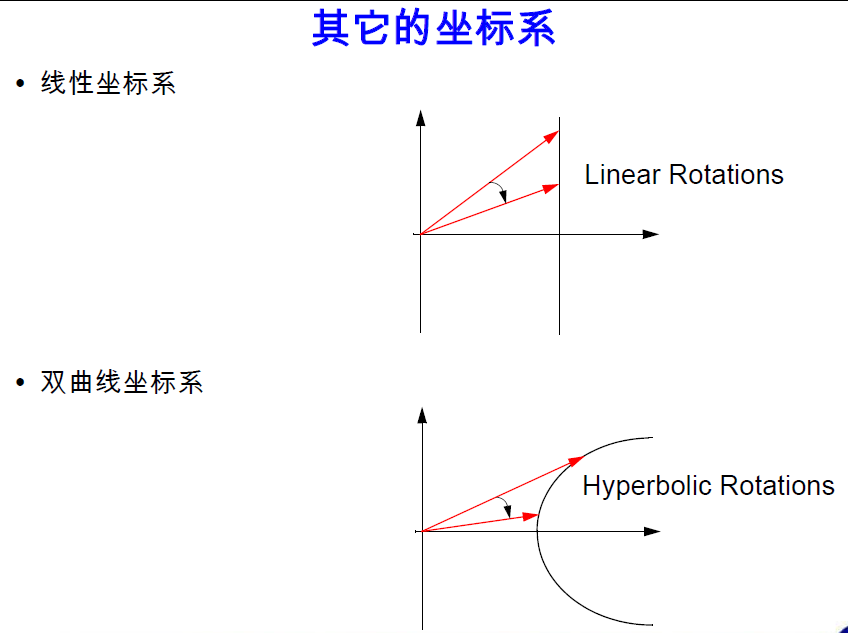
使用其它坐標系的 CORDIC 算法的優點是可以計算更多的函數, 而缺點則是系統將變得更加復雜。當把CORDIC 算法用于線性或雙曲坐標系時, 在圓周坐標系中的旋轉角度集將不再有效。所以, 這些系統應使用其它的兩種旋轉角度集。
我們會發現,可以推導出可在 3 個坐標系中表示 CORDIC 方程的通用公式。這意味著在方程式中引入兩個新變量。其中一個新變量 (e(i)) 代表了適當的坐標系中用于表示旋轉的角度集。
當把CORDIC算法用于雙曲線旋轉時,伸縮因子K與圓周旋轉的因子有所不同。

我們通過引入一個新變量μ,得到CORDIC的通用方程:

至此,三個坐標系下的CORDIC方程得到大一統。



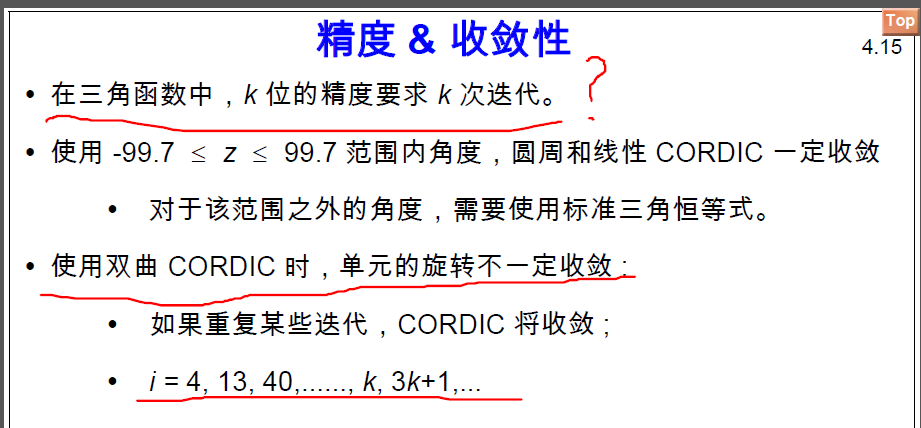
在使用FPGA進行CORDIC算法實現時,理想CORDIC 架構取決于具體應用中速率與面積的權衡。
可以將 CORDIC 方程直接翻譯成迭代型的位并行設計,然而:
位并行變量移位器不能很好地映射到 FPGA 中
需要若干個 FPGA 單元。導致設計規模變大而設計時間變長。
審核編輯:劉清
-
信號處理
+關注
關注
48文章
1000瀏覽量
103201 -
DDS
+關注
關注
21文章
631瀏覽量
152538 -
DFT
+關注
關注
2文章
224瀏覽量
22679 -
CORDIC算法
+關注
關注
0文章
17瀏覽量
9713
原文標題:什么是CORDIC算法
文章出處:【微信號:處芯積律,微信公眾號:處芯積律】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
CORDIC理論分析
基于改進的CORDIC算法的FFT復乘及其FPGA實現
FPGA設計中必須掌握的Cordic算法
高性能HPOR CORDIC算法及實現
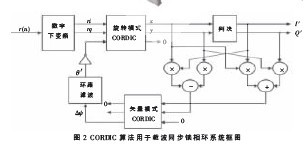
基于CORDIC算法的載波同步鎖相環設計
基于CORDIC算法2FSK調制器的FPGA設計

雙模式CORDIC算法的FPGA實現
cordic算法verilog實現(簡單版)
高速低功耗CORDIC算法的研究與實現
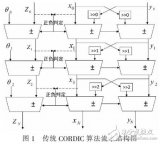
基于FPGA的Cordic算法實現的設計與驗證




 CORDIC算法簡介
CORDIC算法簡介











評論