**1 **分?jǐn)?shù)槽繞組的循環(huán)數(shù)序

**1.1 **什么是分?jǐn)?shù)槽繞組的循環(huán)數(shù)序

利用槽電勢星型圖可以確定分?jǐn)?shù)槽繞組每相所屬的槽號及連接規(guī)律，檢查繞組對稱情況等。對于槽數(shù)比較少的分?jǐn)?shù)槽電機，這種方法簡便、易行、直觀，特別是在微特電機中，常采用多極少槽q＜1的所謂“分?jǐn)?shù)槽集中繞組”，最適合用槽電勢星型圖來進行分相和確定繞組連接關(guān)系。但當(dāng)槽數(shù)很多時，畫槽電勢星型圖就顯得非常麻煩，例如一些大型的水輪發(fā)電機、直驅(qū)風(fēng)力發(fā)電機等，它們的槽數(shù)動輒數(shù)百上千個槽，畫槽電勢星型圖費時費力。其實將各槽分相的方法有很多，槽電勢星型圖法只是其中的一種，接下來我們就再介紹一種實踐中常用的“循環(huán)數(shù)序”的分相方法。

分?jǐn)?shù)槽繞組的每極每相槽數(shù)q為分?jǐn)?shù)，意味著每相在每個極下分得的槽數(shù)不相等，主要表現(xiàn)為同一極下不同相所占的槽數(shù)不相等，有些相多一個槽，有些相少一個槽；同一相在不同極下分得的槽數(shù)也不一樣，有些極下多一槽，有些極下少一槽。這兩種體現(xiàn)方式歸根結(jié)底就是相帶大小不同，有些相帶多一槽，我們稱之為大相帶；有些相帶少一槽，我們稱之為小相帶。各相帶沿定子整個圓周依次分得的槽數(shù)組成了一個數(shù)字序列，這一數(shù)字序列沿定子圓周又是呈周期性的，每過d(q的分母)個數(shù)字就會重復(fù)一次。我們把這種沿定子圓周一個循環(huán)周期內(nèi)各相依次分得的槽數(shù)組成的數(shù)字序列，稱為分?jǐn)?shù)槽繞組的循環(huán)數(shù)序。這么說可能太抽象，不好理解，接下來我們?nèi)杂蒙掀v的Z 1 =30槽，2p=8極的分?jǐn)?shù)槽繞組作為示例，具體來講一講分?jǐn)?shù)槽繞組的循環(huán)數(shù)序以及如何利用循環(huán)數(shù)序?qū)Ψ謹(jǐn)?shù)槽繞組進行分相。

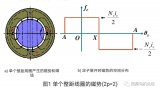
首先把上一篇講的Z 1 =30槽，2p=8極的分?jǐn)?shù)槽繞組的槽電勢星型圖再次展示如下圖1所示。

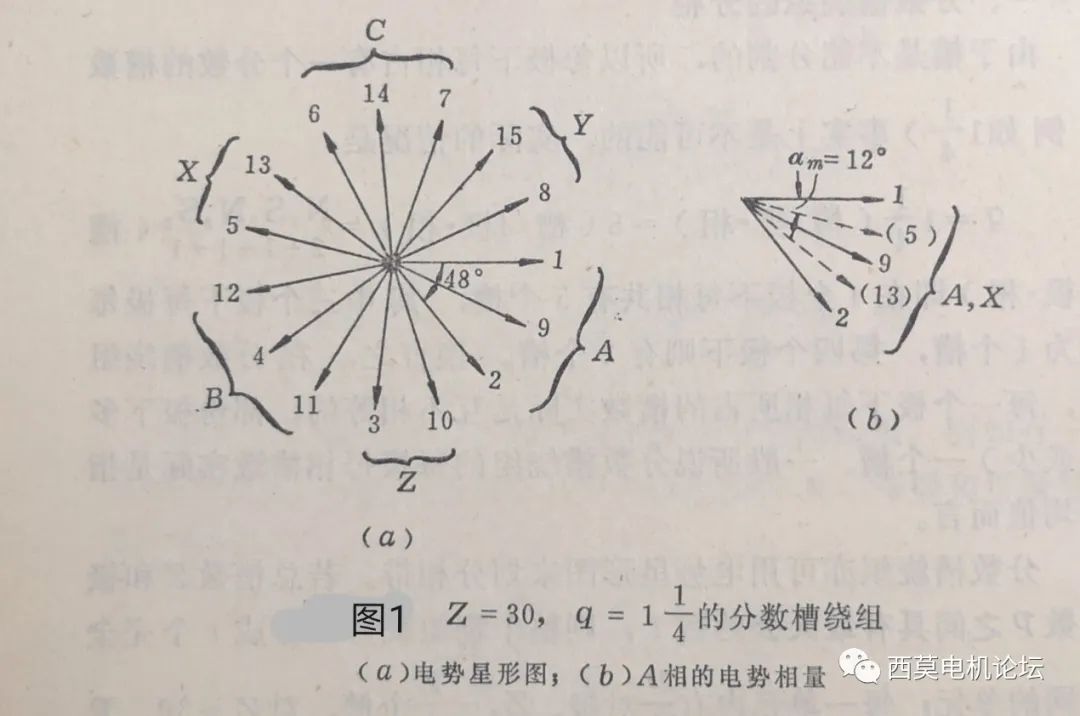
按照圖1a的分相結(jié)果，把各極下每相分得的槽數(shù)列表1如下：

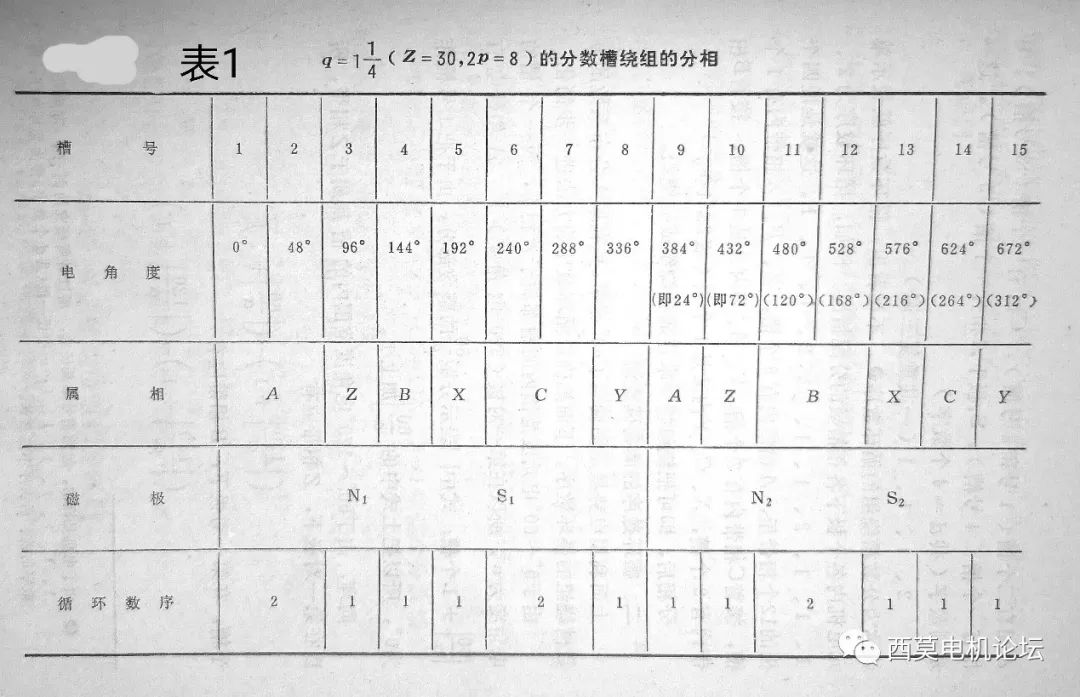
比較圖1a和表1可見，二者是完全對應(yīng)的。N1極下A相分得二個槽(1#槽和2#槽)，Z(-C)相分得一個槽(3#槽)，B相分得一個槽(4#槽)，S~1~極下X(-A)相分得一個槽(5#槽)。這一系列數(shù)字(共d=4個數(shù)字)：2、1、1、1，就稱為該分?jǐn)?shù)槽繞組的循環(huán)數(shù)序，把這四個數(shù)字組成的循環(huán)數(shù)序重復(fù)三遍即得到一個單元電機的相帶分配結(jié)果。也就是說，循環(huán)數(shù)序就是表示電機內(nèi)各極下各相槽數(shù)的分配規(guī)律的一系列數(shù)字，就本例而言，循環(huán)數(shù)序為2、1、1、1，2、1、1、1，2、1、1、1…代表沿定子圓周第一個槽開始，依次給A—Z—B—X—C—Y…各相帶分配的槽數(shù)。這樣只要確定了循環(huán)數(shù)序，不用畫槽電勢星型圖也能進行相帶劃分，因此用循環(huán)數(shù)序進行相帶劃分是一種簡潔的分相方法，特別適用于槽數(shù)比較多的分?jǐn)?shù)槽繞組。需要說明的是，由于電機定子是一個閉合的圓周，而第一個起始槽的位置也是可以任意定義的，因此，對本例而言循環(huán)數(shù)序可以截取2、1、1、1、2、1、1、1…中任一段(共d個數(shù)字)作為循環(huán)數(shù)序，即：1、1、1、2；1、1、2、1；1、2、1、1等都可以作為該分?jǐn)?shù)槽繞組的循環(huán)數(shù)序。也就是說，同樣一個分?jǐn)?shù)槽繞組，其循環(huán)數(shù)序不是唯一，可以有多種組合，截取循環(huán)數(shù)序時的起始點可以不同，但數(shù)字的前后次序不能互換。

1.2 循環(huán)數(shù)序與q的關(guān)系

知道了什么叫分?jǐn)?shù)槽繞組的循環(huán)數(shù)序，接下來我們介紹一下循環(huán)數(shù)序與每極每相槽數(shù)q的關(guān)系，也就是知道了q之后，如何確定循環(huán)數(shù)序。由表1不難看出，在利用循環(huán)數(shù)序沿定子圓周進行相帶劃分時，各相帶分得的槽數(shù)是不同的，一部分相帶包括的槽數(shù)是2，另一部分包括的槽數(shù)是1，即存在兩種寬度不同的相帶，我們把多1槽的相帶稱為大相帶，少1槽的相帶稱為小相帶。不失一般性地說，對于q=b+c/d的分?jǐn)?shù)槽繞組，要實現(xiàn)每個相帶包含的平均槽數(shù)為q，就必須使一部分相帶(大相帶)分得b+1個槽，而另一部分相帶(小相帶)分得b個槽。又因q=b+c/d=(bd+c)/d=N/d，先給每個相帶都分b個槽，則d個相帶就分去了bd個槽，還剩下c個槽沒有被分配下去，要想實現(xiàn)平均每極每相槽數(shù)為q，必須要給c個相帶中每個相帶再加一個槽，即構(gòu)成c個大相帶，d-c個小相帶。由此得出結(jié)論，當(dāng)已知每極每相槽數(shù)q后，則循環(huán)數(shù)序數(shù)字個數(shù)即為d(q的分母)，包括的總槽數(shù)為N(q的分子)，也就是把N個槽分成d份，由于d和N不可約，且每一份只能是整數(shù)個槽，所以不能均分，只能某些份比另一些份多一個槽。這樣形成的一些分配組合就可以作為該分?jǐn)?shù)槽繞組的循環(huán)數(shù)序。

打個比方，這就相當(dāng)于把N元錢分成d個紅包，每個紅包里必須是整數(shù)元錢，而且大紅包只能比小紅包多一塊錢，這樣每個紅包里的錢數(shù)組成的數(shù)字序列即為循環(huán)數(shù)序。

仍以上例8極、30槽，q=1+1/4=5/4分?jǐn)?shù)槽繞組為例，把5個槽分成4份的分法可以是q=(2+1+1+1)/4，這樣循環(huán)數(shù)序就是2、1、1、1，當(dāng)然也可以按1、2、1、1；1、1、2、1；1、1、1、2等組合來分配，這些組合都可以作為該分?jǐn)?shù)槽的循環(huán)數(shù)序。需要特別說明的是，并不是所有分?jǐn)?shù)槽繞組都可以按上述把N槽分成d份，所有分配組合都可以作為其循環(huán)數(shù)序，只有當(dāng)c=1或c=d-1時才能把所有的分配組合都可以作為循環(huán)數(shù)序。當(dāng)c≠1或c≠d-1時，按上述方法，只有一部分分配組合可以作為循環(huán)數(shù)序，因此這種確定循環(huán)數(shù)序的方法還是有局限性的，需要另外尋求其它確定循環(huán)數(shù)序的方法。

**1.3 **循環(huán)數(shù)序的確定方法

如前所述，同一個分?jǐn)?shù)槽繞組的循環(huán)數(shù)序有很多種，實踐中確定循環(huán)數(shù)序的方法也有很多，這里介紹常用的幾種：

①對于q=b+c/d，其中c=1或c=d-1的分?jǐn)?shù)槽繞組

循環(huán)數(shù)序由d個數(shù)字組成，共bd+c=N個槽，其中c個大相帶，每個大相帶有(b+1)個槽；d-c個小相帶，每個小相帶有b個槽。

當(dāng)c=1時，循環(huán)數(shù)序中數(shù)字的排列順序一般是(d-c)個小相帶的槽數(shù)在前面，c=1個大相帶的槽數(shù)在后面，例如：

q=2+1/4時，循環(huán)數(shù)序為(2、2、2、3)…

q=1+1/5時，循環(huán)數(shù)序為(1、1、1、1、2)…

q=2+1/5時，循環(huán)數(shù)序為(2、2、2、2、3)…

當(dāng)c=d-1時，一般是c個大相帶的槽數(shù)排在前面，d-c=1個小相帶的槽數(shù)排在后面，例如：

q=1+3/4時，循環(huán)數(shù)序為(2、2、2、1)…

q=2+3/4時，循環(huán)數(shù)序為(3、3、3、2)…

q=2+16/17時，循環(huán)數(shù)序為(3、3、3、3、3、3、3、3、3、3、3、3、3、3、3、3、2)…

當(dāng)然上面所講的循環(huán)數(shù)序也可以從任意一個數(shù)字開始依次截取d個數(shù)字作為循環(huán)數(shù)序。

②對于q=b+c/d，其中c≠1且c≠d-1的分?jǐn)?shù)槽繞組

這種分?jǐn)?shù)槽繞組的循環(huán)數(shù)序可用列表方法獲得。有兩種列表法：

列表法Ⅰ：首先列一個c行d列的表格，從左邊第一列開始，從上到下填寫等于(b+1)的數(shù)字c個，在第二列填寫等于b的數(shù)字(d-c)個，然后接著又填寫等于(b+1)的數(shù)字c個及等于b的數(shù)字(d-c)個，…余類推，直到c行d列完全填滿為止。這時取表中任意一行的數(shù)字，都可以作為循環(huán)數(shù)序。舉例說明：

例如：q=1+4/7時，b=1，b+1=2，d=7，c=4，d-c=3，可作出4行7列的表格如下：

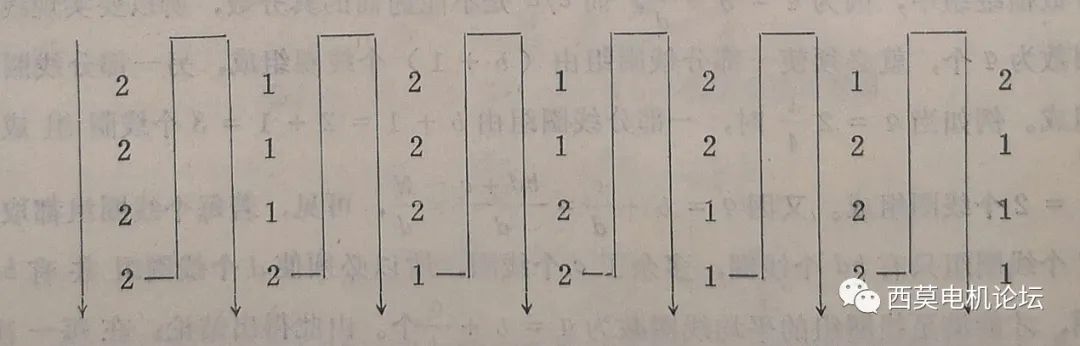
這時循環(huán)數(shù)序可取為(2、1，2、1、2、1、2)；(2、1、2、1、2、2、1)；(2、1、2、2、1、2、1)；(2、2、1、2、1、2、1)等等都是可以的。

又如：q=2+2/5時b=2，b+1=3，d=5，c=2，d-c=3，可按上述規(guī)則作出2行5列的表格如下：

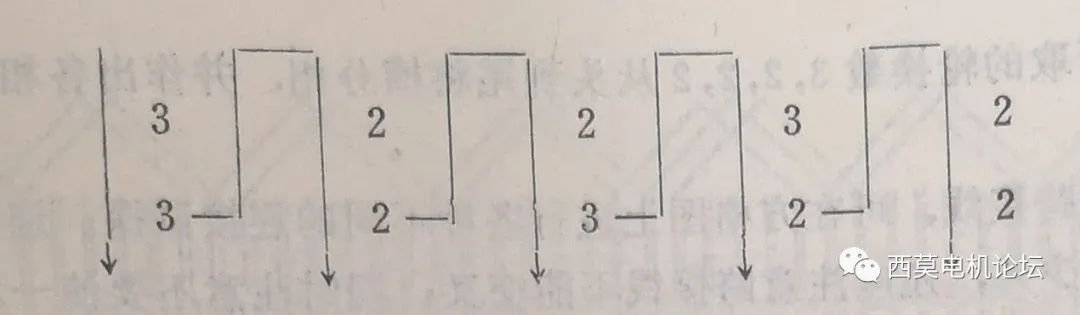
同理循環(huán)數(shù)序可取為(3、2、2、3、2)或(3、2、3、2、2)兩種都可以。

對于上述類型的分?jǐn)?shù)槽繞組，也可以采用另一種列表的方法：

列表法Ⅱ：列出(d-c)行、d列的表格。從左邊開始，自上到下，先填寫等于b的數(shù)字(d-c)個，接著填寫等于(b+1)的數(shù)字c個，然后又填寫等于b的數(shù)字(d-c)個及等于(b+1)的數(shù)字c個，直到填滿(d-c)行和d列的表格為止。同樣，表中任意一行的數(shù)字均可作為循環(huán)數(shù)序。

例如：q=1+4/7，這時，d=7，c=4，d-c=3，列出3行7列的表格如下：

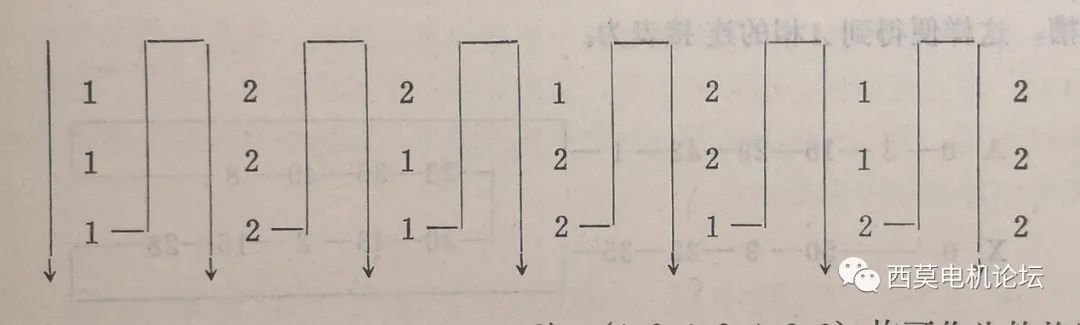
同理，(1、2、2、1、2、1、2)；(1、2、1、2、2、1、2)；(1、2、1、2、1、2、2)均可作為循環(huán)數(shù)序。

**2 **分?jǐn)?shù)槽繞組的構(gòu)成

與整數(shù)槽繞組一樣，分?jǐn)?shù)槽繞組按槽內(nèi)導(dǎo)體層數(shù)分也可以分為單層繞組和雙層繞組；按線圈組的連接規(guī)律分也可以分為疊繞組和波繞組。這里我們重點介紹雙層疊繞組和雙層波繞組的構(gòu)成。

**2.1 **疊繞組的構(gòu)成

分?jǐn)?shù)槽疊繞組的構(gòu)成比較簡單，基本與整數(shù)槽繞組的連接規(guī)律一樣。仍以Z 1 =30，2p=8，q=1+1/4的分?jǐn)?shù)槽繞組為例，連接成疊繞組時A相繞組的展開圖如圖2所示。

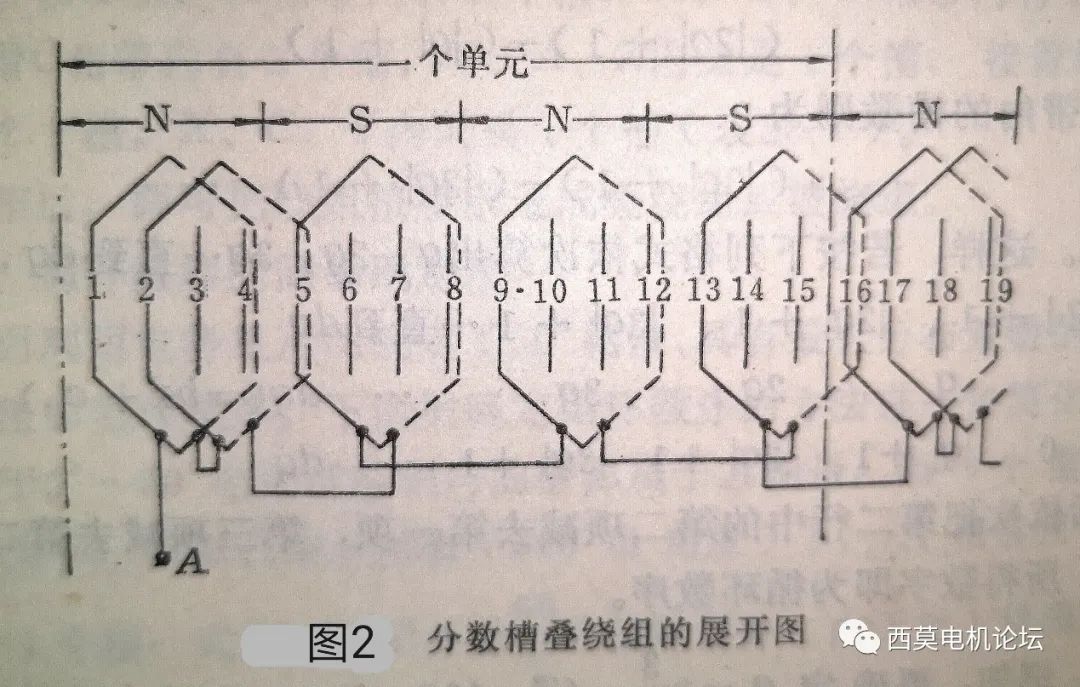
由表1和圖2可見，單元電機內(nèi)屬于A相的共有4個線圈組，其中一個是大線圈組，由兩個線圈串聯(lián)組成；三個是小線圈組，每組內(nèi)只有一個線圈。不同磁極下的線圈組串聯(lián)時應(yīng)該反串，即尾一尾相連或首一首相連，這和整數(shù)槽繞組相同。

圖1(b)表示A相繞組內(nèi)各線圈的電勢相量，圖中5#和13#線圈屬于X相帶，由于接線時已反串，所以在相量圖上其位置翻轉(zhuǎn)了180°，在圖1b中用虛線表出。由圖1b可見，對所研究的例子，計算A相繞組的合成電勢和主波的分布系數(shù)時，應(yīng)該用1、(5)、9、(13)、2等五個互相間隔12o電角度的電勢相量來考慮。這是分?jǐn)?shù)槽繞組的一個普遍規(guī)律，即普遍來講，單元電機內(nèi)A相共有N個(N=bd+c)互相間隔αm電角度的電勢相量，α ~m~ =60o/N，故計算一相繞組的合成電勢時，應(yīng)該用這N個間隔α~m~電角度的電勢相量疊加來考慮分?jǐn)?shù)槽繞組的分布系數(shù)。以上分析可見，分?jǐn)?shù)槽繞組雖然有時槽數(shù)較少，特別是微特電機中廣泛采用多極少槽設(shè)計，通常是q＜1的所謂“分?jǐn)?shù)槽集中繞組”，槽數(shù)基本與極數(shù)相當(dāng)，槽數(shù)雖少，但可以得到和q比較大的整數(shù)槽繞組同樣的分布系數(shù)和分布效果，這也是分?jǐn)?shù)槽繞組的一大優(yōu)勢和特征。關(guān)于分?jǐn)?shù)槽繞組的電勢、磁勢以及繞組系數(shù)的計算分析，后續(xù)文章還會詳細講解。

**2.2 **波繞組的構(gòu)成

與整數(shù)槽波繞組相比，由于分?jǐn)?shù)槽繞組的實際每極每相槽數(shù)不相等，因此分?jǐn)?shù)槽波繞組的連接就復(fù)雜多了，尤其在槽數(shù)較多的情況下，有多種波繞組的連接方式，為了得到最佳的連接方案，往往需要在多種連接方案中進行對比優(yōu)選。如果把每種連接方式都繪出整個接線圖非常費時費力，實踐中通常采用一種叫做方格圖的辦法來確定和顯示波繞組的連接規(guī)律。

接下來我們以Z 1 =54，2p=8，的三相分?jǐn)?shù)槽繞組為例，介紹一下方格圖的作法以及用方格圖進行波繞組連接的原理。

①計算每極每相槽數(shù)

q=2+1/4。

②確定循環(huán)數(shù)序

按前述方法得到該分?jǐn)?shù)槽繞組的循環(huán)數(shù)序為3、2、2、2。

③確定合成節(jié)距Y

Y=Y 1 +Y 2 =13≈2τ

④畫方格圖

先按1、2、3、4…順序?qū)懗鼍€圈編號，也就是線圈上層邊所在的槽號，取每行的槽號數(shù)等于合成節(jié)距Y(對于本例Y=13)，然后繼續(xù)依次往下寫槽號，直到寫完Z1個槽號(對于本例Z 1 =54)，為了更直觀地看清連接規(guī)律，通常在寫完所有(54個)槽號后，繼續(xù)往下多寫一行或多寫幾個槽號，如圖3所示。

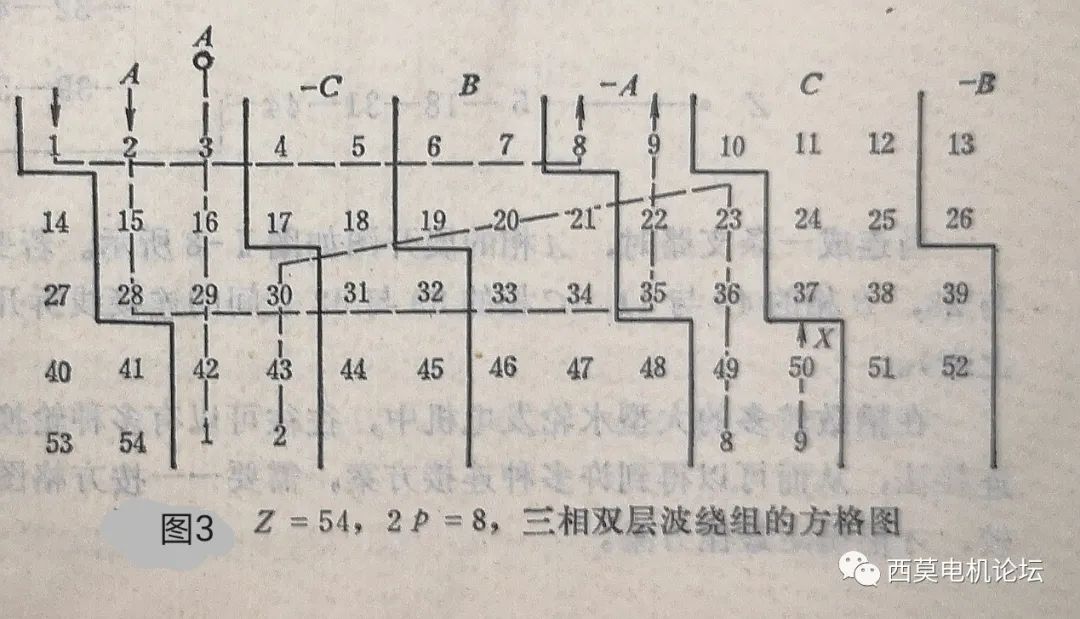
⑤相帶劃分

在方格圖上按循環(huán)數(shù)序3、2、2、2從頭到尾將各槽號劃分相帶，由于各相帶的大小不同，因此六個相帶的分割線是階梯型的折線。

⑥線圈連接

為了得到最佳的連接方案，可在方格圖上進行各種不同連接方式的試探。線圈連接的原則：一是跨接線盡量短；二是跨接線數(shù)目盡量少；三是跨接線盡量不交叉或少交叉；四是一相的所有跨接線要避免在端部形成完整的一圈，以免引起軸向磁場。

根據(jù)以上原則，以A相為例，首先從3#槽開始作為A相首端出線頭，縱向的各槽，例如3—16—29—42—1，它們之間都相差一個合成節(jié)距(13槽)，所以這些線圈都是很自然地按照波繞組的連接規(guī)律連接起來，類似這種自然連接的線圈還有30—43—2—15—28；50—9—22—35；23—36—49—8等等。這四段線圈組都是按照波繞組的連接規(guī)律自然連接起來的。接下來就是用跨接線把這四段線圈組串聯(lián)起來。顯然1#線圈與8#相隔僅7個槽，距離較近，可以用一根跨接線連接起來；同理再分別用兩根跨接線將23#線圈與30#線圈、28#線圈與35#線圈連接起來，就構(gòu)成了并聯(lián)支路數(shù)為1的全串聯(lián)A相繞組。其線圈連接的次序和連接規(guī)律見下表

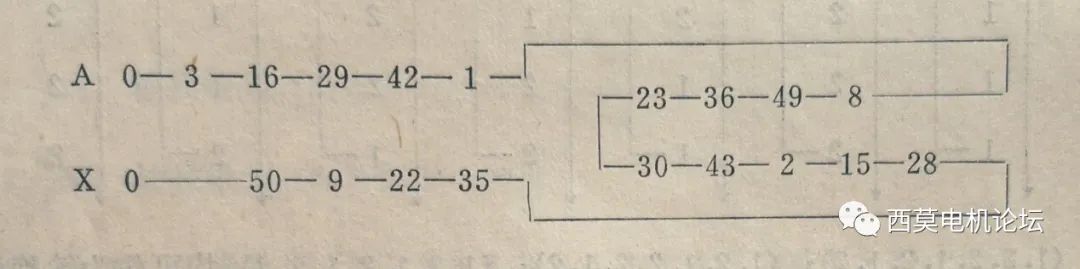
同理可以進行B相和C相的連接，為了保證三相互差120o，B相可以從21#槽作為出線頭開始連接；C相從12#槽起始。因為3#、21#、12#槽電勢互差120o電角度。這樣就可以得到B相和C相的連接表如下：

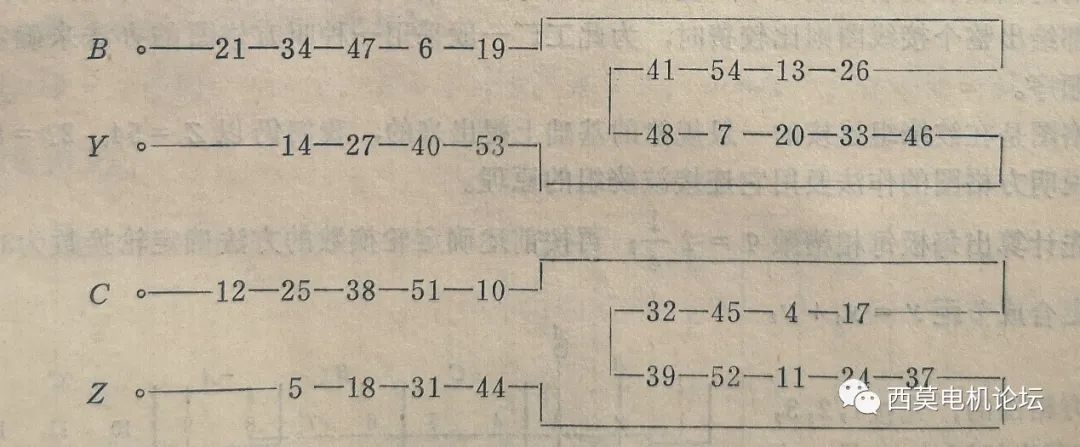
⑦畫繞組展開圖

以上三相連接方式是并聯(lián)支路數(shù)為1的連接方式，這種連接的繞組展開圖如圖4所示。為了清楚起見，圖中只畫出了A相繞組展開圖。

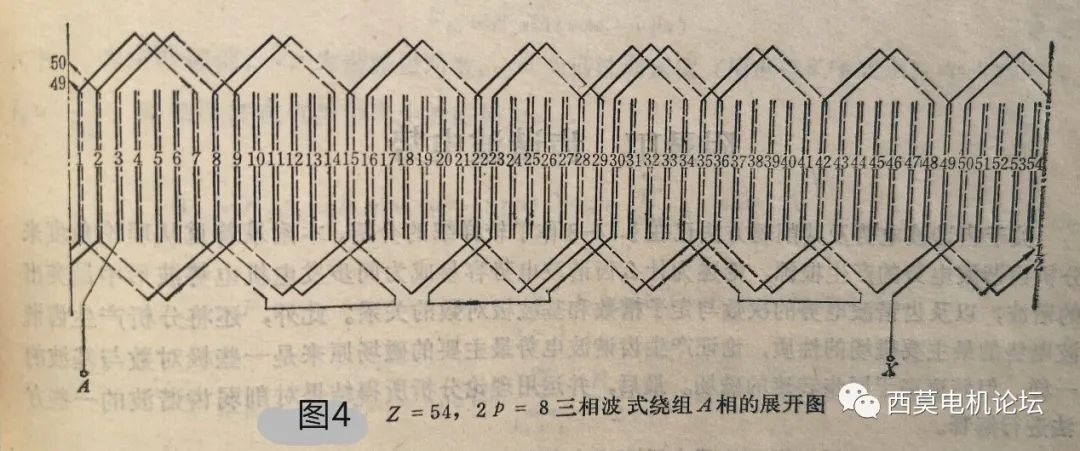
如果要連接成兩路并聯(lián)的方式，則應(yīng)將A相的23與30；B相的41與48；C相的32與39之間的三根跨接線斷開，這樣每相就可以得到兩條并聯(lián)支路。

在槽數(shù)較多的大型水輪發(fā)電機和低速直驅(qū)電機中，往往可以有多種循環(huán)數(shù)序，每一種循環(huán)數(shù)序又可能有多種連接方式，從而可以得到許多種連接方案，需要逐一在方格圖上進行連接對比，最終確定最佳連接方案。

本期介紹了分?jǐn)?shù)槽繞組的另外一種相帶劃分和槽分配的方法——循環(huán)數(shù)序法；還介紹了分?jǐn)?shù)槽疊繞組和波繞組的構(gòu)成方法。由于疊繞組的構(gòu)成與整數(shù)槽疊繞組構(gòu)成方法基本相同，相對較為簡單；而分?jǐn)?shù)槽波繞組的構(gòu)成相對要復(fù)雜很多，因此重點介紹了分?jǐn)?shù)槽波繞組的構(gòu)成方法。需要特別說明的是，本期介紹的這些內(nèi)容和方法，非常適合槽數(shù)和極數(shù)都比較多，q＞1的分?jǐn)?shù)槽繞組，如大型水輪發(fā)電機、低速直驅(qū)永磁電機等進行相帶劃分和繞組連接，并不太適用于微特電機那種槽數(shù)較少、多極少槽的分?jǐn)?shù)槽集中繞組，因為這種分?jǐn)?shù)槽繞組往往q＜1，b=0，雖然也可以用循環(huán)數(shù)序，但由于b=0使得循環(huán)數(shù)序中出現(xiàn)0數(shù)字，非常容易出錯。由于這種電機槽數(shù)較少，遠不如用槽電勢星型圖進行相帶劃分和槽分配更加簡單直觀。由于槽數(shù)較少，更不用興師動眾地搞什么方格圖做波繞組連接。