將0.1累加100次也得不到10

我們來一個計算機運算錯誤的例子。

function sum(){
    let sum = 0;
    for(let i=1;i<=100;i++){
        sum +=0.1;
    }
    console.log(sum)
}

我們在瀏覽器的控制臺中，運行sum(),得到的運行結果為9.99999999999998。這顯然和我們的九年義務教育所教導的 「背道而馳」 。

有句話說， 「雪崩的時候，沒有一片雪花是無辜的」 。在這段代碼中，程序沒錯，計算機也沒有發生故障，當然和所使用的語言也沒有關系（選用其他的高級語言可能運算結果不同）。如果硬要找一個背鍋的，那就是 「計算機處理小數的機制」 。

用二進制數表示小數

在計算機底層知識之二進制中我們講過，由于計算機內部所有的信息都是以二進制數的形式來處理，因此， 「整數和小數并無差別」 。

在說明計算機如何用二進制數表示小數的具體方法前，我們先嘗試將1011.0011這個有小數點的二進制數轉換成十進制數。

小數點 「前面」 部分的轉換方法在計算機底層知識之二進制中介紹過。只需將各 「數位」 數值和 「位權」 相乘，然后再將相乘的結果相加即可實現。其實，針對小數點后面的部分，也是 「照貓畫虎」 ，也是將各 「數位」 數值和 「位權」 相乘的結果相加即可。

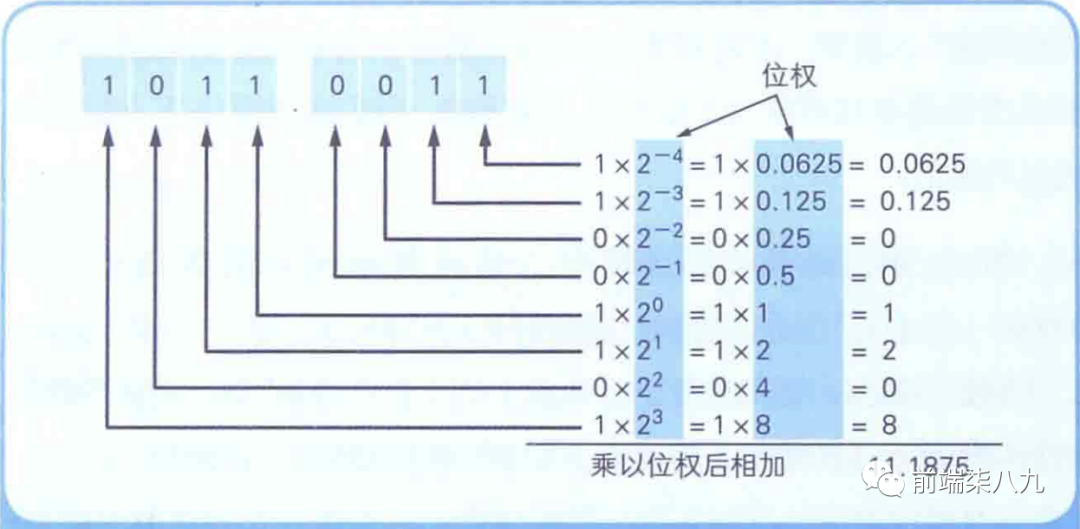
二進制數小數轉換成十進制數

二進制數小數點前面部分的**「位權」**

• 第一位是2的0次冪
• 第二位是2的1次冪
• 第三位是2的2次冪
• 以此類推

而小數點后面部分的**「位權」**

• 第一位是2的-1次冪
• 第二位是2的-2次冪
• 第三位是2的-3次冪
• 以此類推

?0次冪前面的位的位權按照1次冪、2次冪····的方式**「遞增」**

0次冪后面的位的位權按照-1次冪、-2次冪····的方式**「遞減」**

?

計算機運算出錯的原因

?計算機運算出錯的原因：「有一些十進制數的小數無法轉換成二進制」

?

小數點后4位用二進制數表示時的數值范圍為0.0000~0.1111。這里只能表示0.5、0.24、0.125、0.0625這四個二進制數小數點后面的位權組合而成（相加總和）的小數。

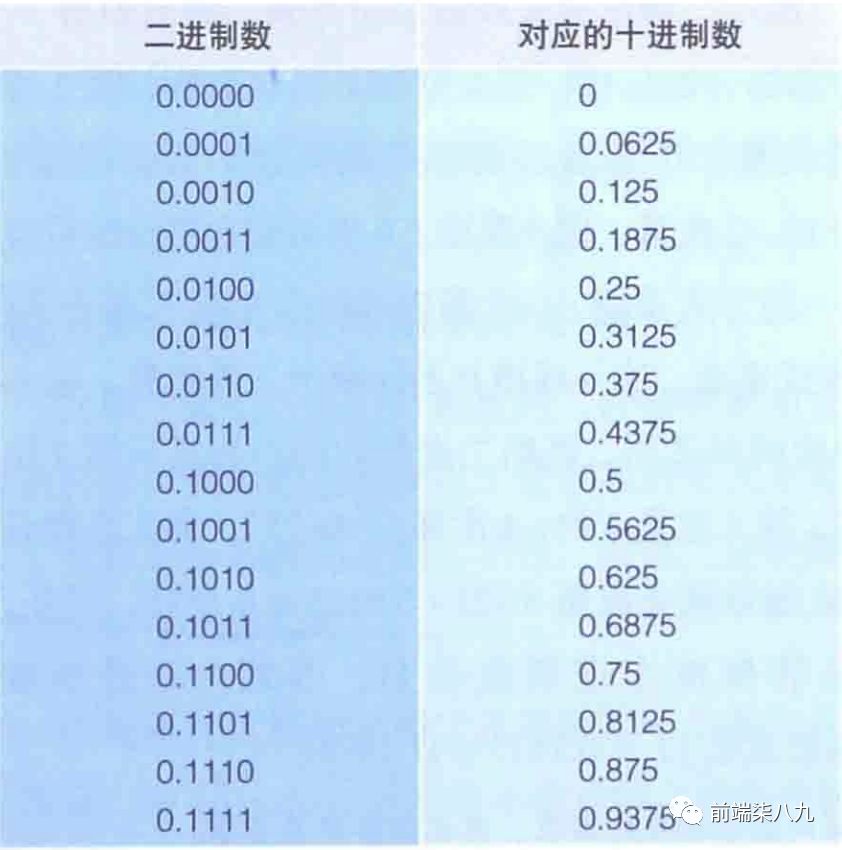
?可以看出：「二進制數是連續的，十進制數是非連續的」

?

在前面講二進制的時候，我們說，根據IC引腳個數不同，我們可以表示位數不同的二進制數。我們可以通過增加引腳數，也就是增加二進制小數點后面的位數，與其相對應的十進制數的個數也會增加， 「但是不管增加多少位，2的-〇〇次冪怎么相加都無法得到0.1這個結果」 。

實際上，十進制數0.1轉換成二進制后，會變成0.00011001100···（1100循環）這樣的 「循環小數」 。這和用十進制數來表示1/3是一樣的道理。

?計算機這個 「功能有限」 的機器設備，是無法處理 「無限循環」 的小數的

?

因此，在遇到 「循環小數」 時，計算機就會根據 「變量數據類型」 所對應的長度將數值從 「中間截斷」 或者 「四舍五入」 。

然后，我們再結合我們上面的例子，一個 「循環小數」 在進行存儲的時候，已經被 「掐頭去尾」 ，而偏偏針對這個值，又進行了N多次處理。不怕你不努力，就怕你，持之以恒的向偏離既定軌道的方向上移動，那么結果可想而知，是永遠不會達到最終想要的結果。

浮點數

像1011.0011這樣帶小數點的表現形式，在計算機內部是無法使用的。

很多編程語言中都提供了兩種表示小數的數據類型，分別是 「雙精度浮點數」 和 「單精度浮點數」 。

• 「雙精度浮點數」 用64位表示小數
• 「單精度浮點數」 用32位表示小數

「浮點數」 是指用 「符號」 、 「尾數」 、 「基數」 和 「指數」 這四部分表示的小數。

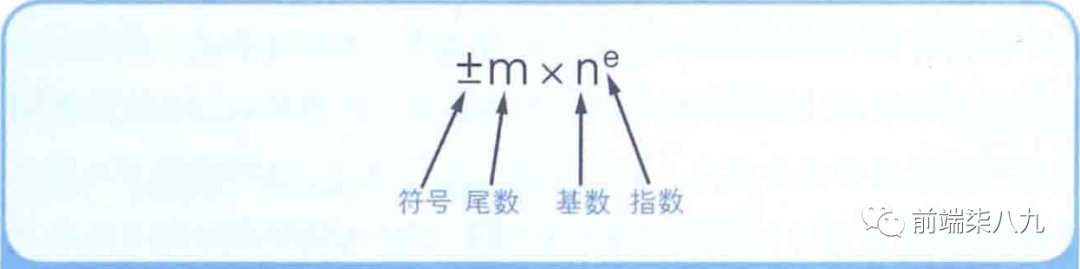
?計算機內部使用的是二進制數，所以 「基數是2」 ，因此，實際的數據中往往不考慮基數。只用 「符號」 、 「尾數」 、 「指數」 這三部分就可以表示 「浮點數」 。

?

浮點數表現形式

浮點數的表現方式有很多中，我們采用IEEE標準來解釋。

雙精度浮點數和單精度浮點數在表示同一個數值時 「使用的位數」 不同。

「符號部分」 是指使用一個 「數據位」 來表示符號。「數據位是1時表示負，為0時表示正或者0」

?數值的大小用 「尾數部分」 和 「指數部分」 來表示。即用 「尾數部分 × 2的指數部分次冪」 的形式來表示。

?

• 「尾數部分」 用的是**「將小數點前面的值固定為1的正則表達式」**
• 「指數部分」 用的是**「EXCESS系統表示」**