正文

自麥克斯韋方程建立以來，求解已知激勵、特定邊界條件下的麥克斯韋方程組的解一直是一百多年以來最受關注的問題之一。

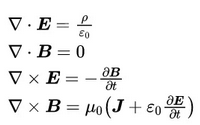
圍繞著麥克斯韋方程組的求解，無數科研工作者前赴后繼的努力，才有了計算電磁學如今的面貌，發展過程大致可以分為四個階段：

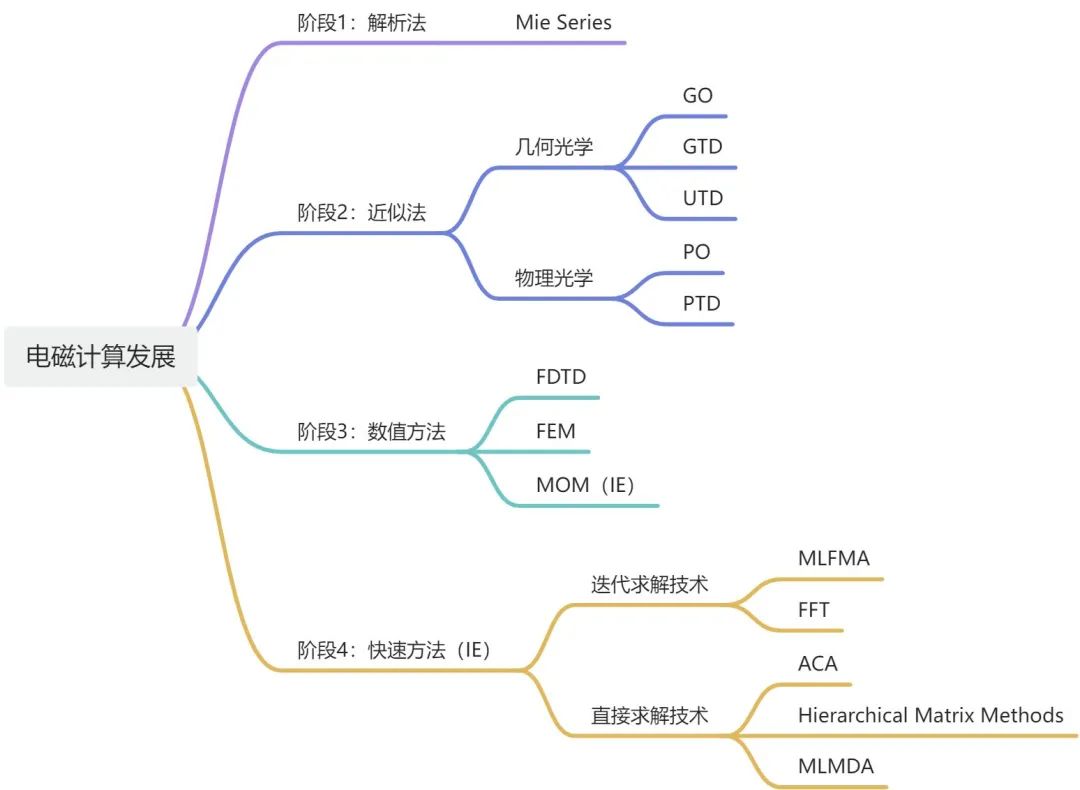
階段1：解析法

對于結構形式簡單的模型，依托高超的數學技能，基于maxwell方程和邊界條件，可以計算出空間場分布，即解析解。其優點在于：結果為嚴格得數學推導，結果完全正確，沒有誤差，因而可以作為標準去驗證各種計算方法得正確性，也常作為RCS測試中定標體，對測試系統進行標定。

1908年，Gustav Mie 給出了均勻圓球對平面波散射得嚴格解（Mie理論）。具體理論推導可以參考江長蔭于1996年發表在《電波科學學報》上得論文。

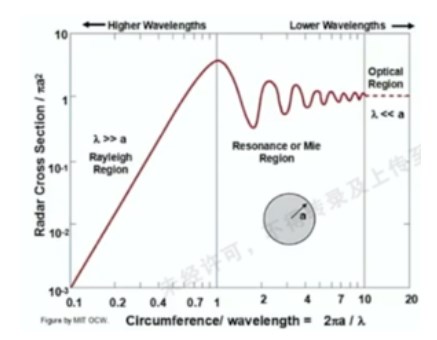
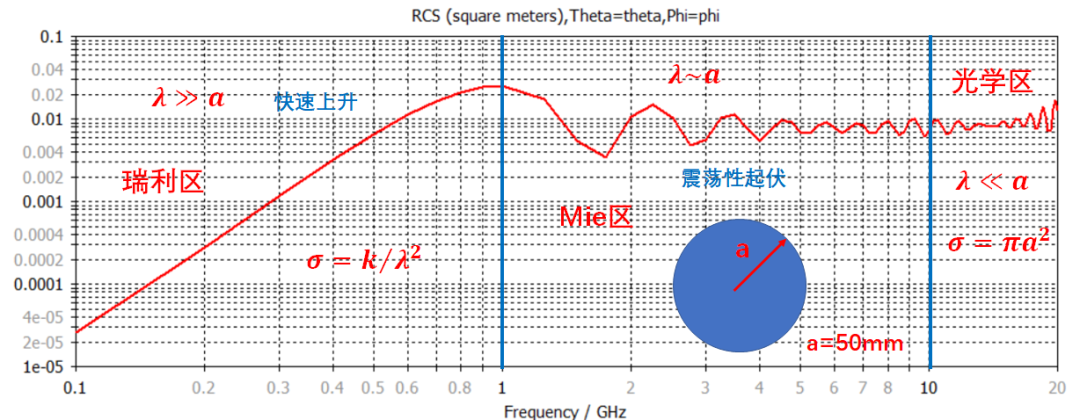
使用CST仿真軟件的時域求解器（Transistor），對球的寬帶單站RCS進行了計算：取球半徑為50mm，計算頻率為0.1GHz~20GHz，參考文獻對求解結果的分區：

1）0.1GHz~1GHz頻段內，波長遠大于球半徑，為瑞利區，此時單站RCS 隨頻率升高而快速變大；

2）1GHz~10GHz頻段內，波長與半徑相當，為Mie區，單站RCS隨頻率升高呈現震蕩性起伏；

3）10GHz~infinity，波長遠小于半徑，為光學區，單站RCS隨頻率變化呈現基本穩定。

使用FEKO仿真軟件對單頻點（10GHz）處金屬球的雙站RCS進行了計算，其雙站RCS的分布形式與往期文章中介紹的陣列天線的方向圖有些相似，與感性的認知不同，其最大散射方向并不是后向，而是前向，即與入射電磁波同向。這是不是就是科幻小說《三體》中，使用太陽作為無線電放大器的理論依據，哈哈。

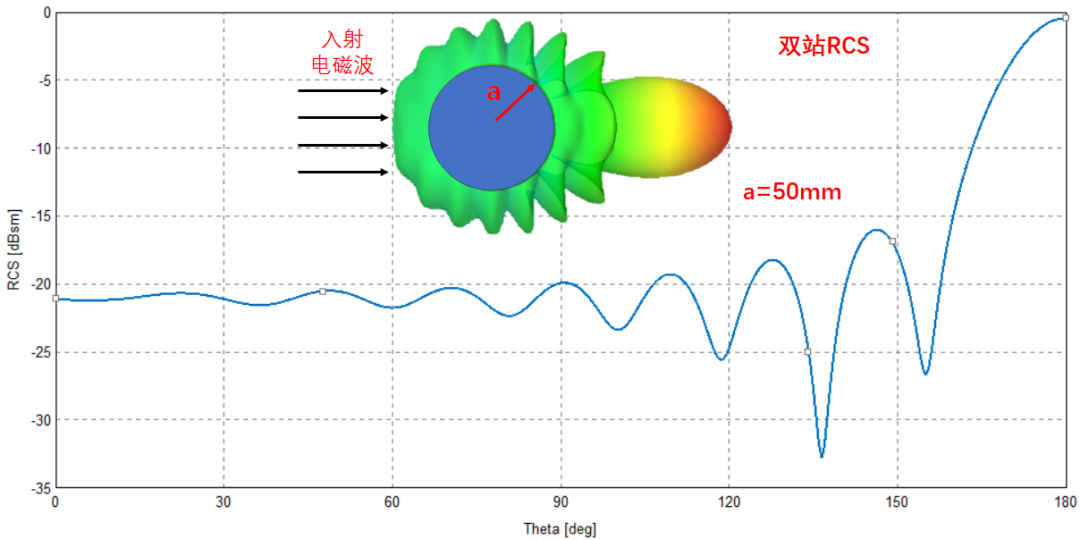
正如往期文章“緣起“收斂性”——Maxwell方程與求解”中所說得那樣，形狀規則如球形的目標，尚可以借助高超的數學技巧，完成解析計算，但是一旦模型的外形變化一下，復雜的外形所帶來的復雜的邊界條件，會導致Maxwell方程組無法解析求解。

階段2：近似方法

在那個“算力”尚不發達的年代，類似“全波仿真”的精確計算方法還沒辦法被實現，近似方法則因為其較低的“算力需求”而被廣泛使用，其中要數幾何光學算法（GO）和物理光學算法（PO）應用最為廣泛。

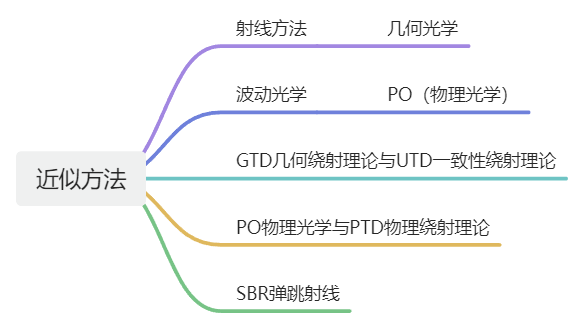
GO（Geometrical Optics幾何光學）

幾何光學的基本思想基于：高頻電磁波的傳播近似于光，因而波的傳播問題可以采用射線追蹤（Ray-Tracing），從而場的振幅可以根據波前表面的形狀來確定。顯然，使用幾何光學方法，陰影區域中的場完全為零，而被照亮區域中的場為單獨的入射場或入射場與反射場的疊加。物體邊沿和尖劈的衍射場被完全忽略，而總場有兩處具有非物理的不連續性：一處是在亮區和陰影區之間的邊界（稱為入射陰影邊界，ISB），另一處是在反射區和反射不能到達的區域之間的邊界（稱為反射陰影區，RSB）。

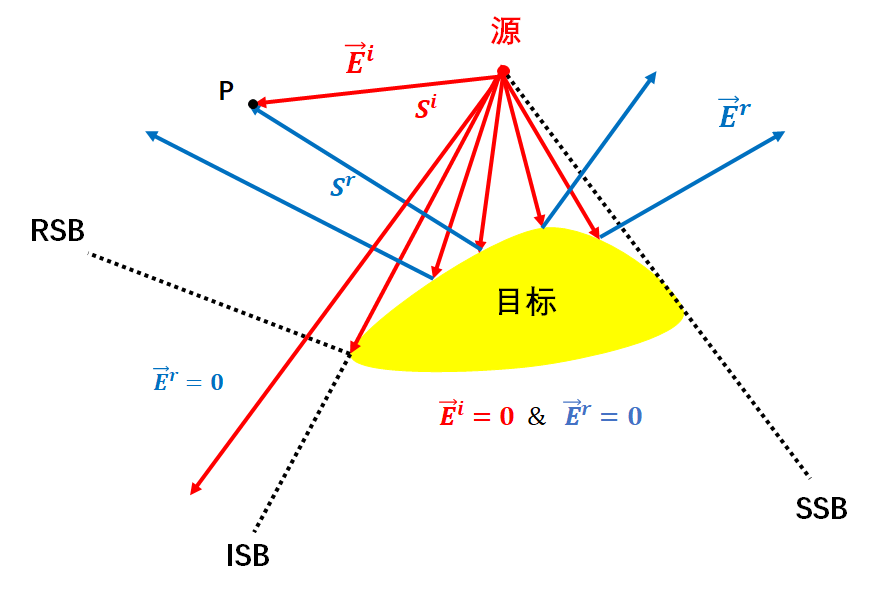
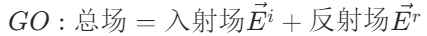
其中入射場和反射場可分別由下列公式求得：

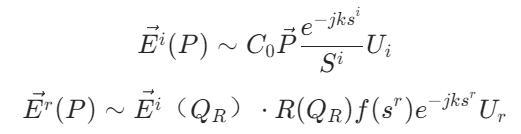
入射場和反射場是否被置零則取決于系數和的取值：

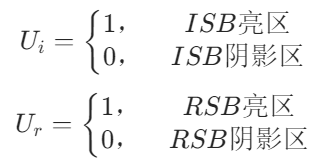
GTD（Geometrical Theory of Diffraction幾何繞射理論）

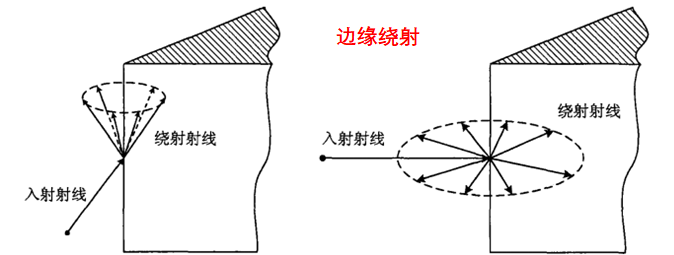
我們可以在幾何光學的解中加入衍射場以提高幾何光學解的精度，由此產生了幾何繞射理論（GTD）。GO的修正繞射線產生于結構不連續處和材料不連續處，以及電磁波掠入射光滑凸表面情形，主要有以下集中類型：

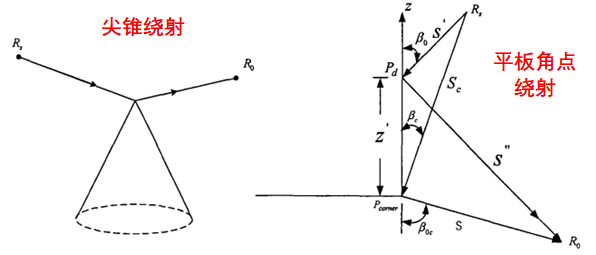
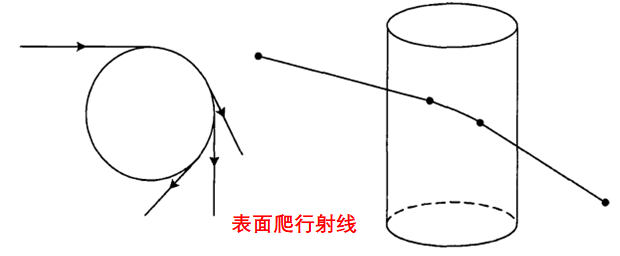
UTD（Uniform Theory of Diffraction一致性繞射理論）

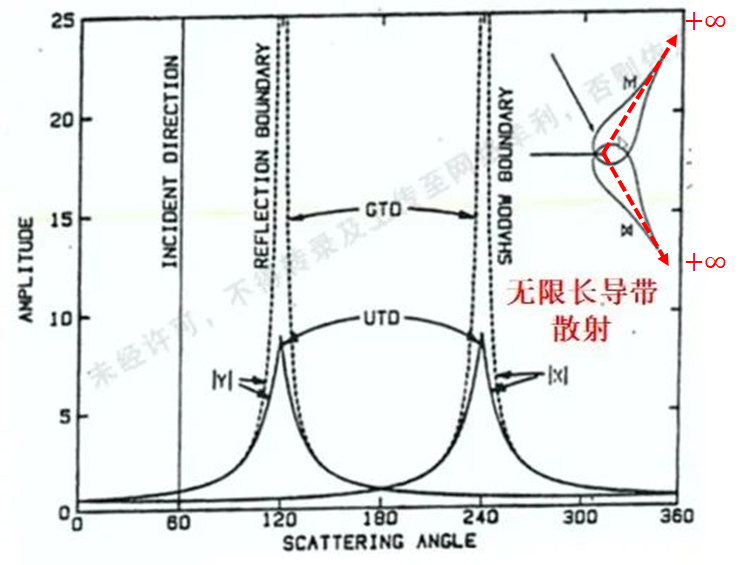
Keller導出的GTD理論，在亮區和陰影區的邊界兩側的過度區失效，如圖所示，以無限長導帶的散射為例，按照GTD理論，則會在兩個邊界處產生無窮大的散射場，與客觀事實不相符，而UTD則會通過比例系數的引入，將過渡區的場控制在一個有限大范圍內，具有更高的計算精度。

PO（Physical Optics物理光學）

另外一類高頻近似技術從物理光學（PO）出發，將電大尺寸導體亮區表面上的感應電流密度近似為，而陰影區的電流密度近似為。進而自由空間中的場分布可以依據源-場關系求得：

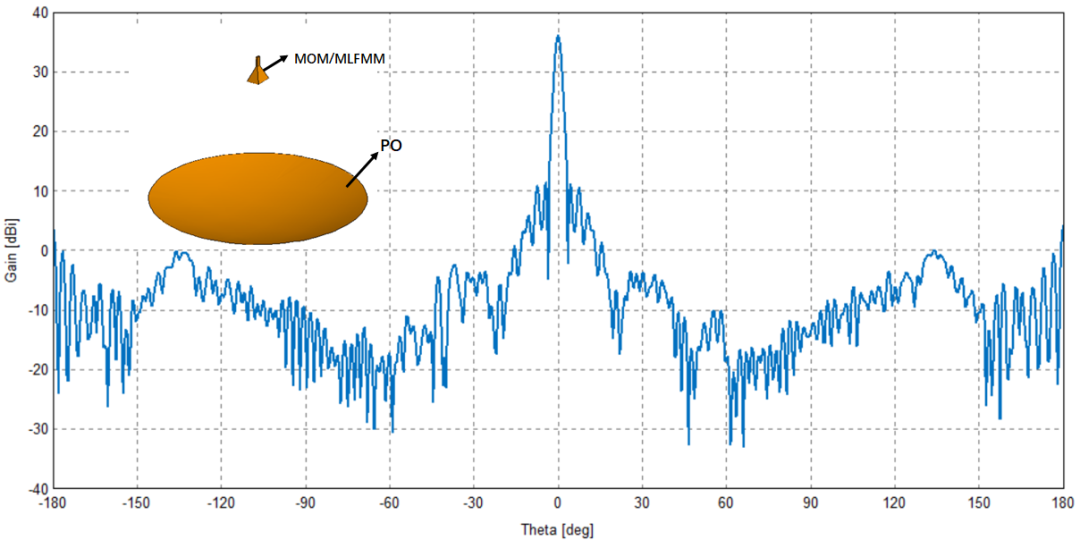
物理光學算法被廣泛應用于反射面天線輻射特性的計算，饋源使用全波算法，反射面使用PO算法，兩種算法混合，從而使得電大尺寸的反射面能夠快速獲得相對準確的計算結果。

PTD（Physical Theory of Diffraction物理衍射理論）

物理光學理論（PO）近似忽略了幾何不連續性對感應電流的影響，因此近似的感應電流在亮區和暗區邊界處存在不連續，這種不連續影響了計算結果的精度，通過在感應電流中加入非均勻的邊緣電流，以此來改善物理光學的計算精度。

后來聞名世界的第一款隱身戰斗機F-117的隱身設計正是基于此理論而完成的設計。

SBR（shooting and bouncing ray彈跳射線算法）

將幾何光學與物理光學的方法結合起來，開發出了功能強大的算法，用于計算大尺寸復雜目標的電磁散射，這種混合技術稱為彈跳射線（SBR）法。在該方法中，從源出發的入射波用指向物體的射線簇表示。當每條射線反彈時，其相關的振幅和相位均被追蹤，而反彈過程受幾何光學的約束。在射線與目標的每一個交點應用物理光學法做積分,以確定射線對散射場或輻射場的貢獻,最終解是所有射線貢獻的總和。這種算法已經被實現并廣泛用于計算雷達散射特征、大型平臺上天線的輻射特性和復雜城市環境中的電磁波傳播。

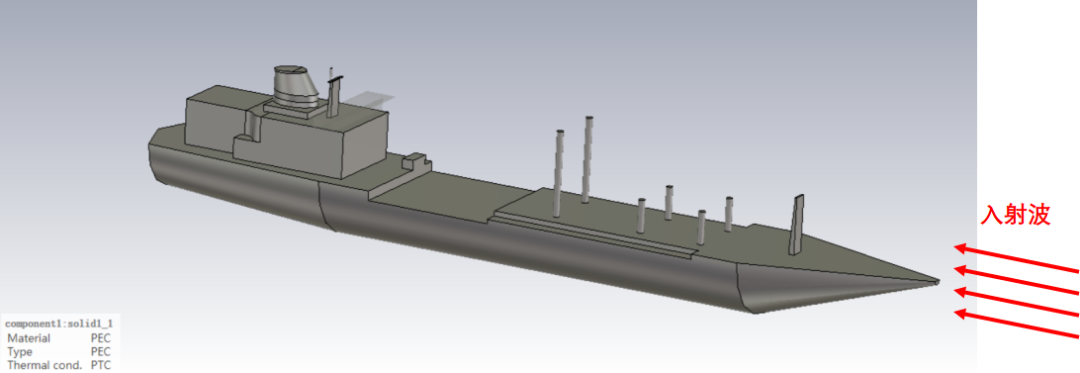
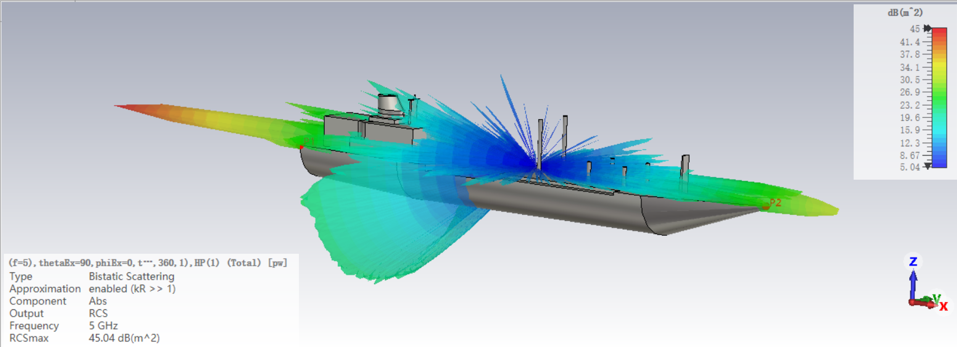
依托CST軟件的Asymptotic Sovler（漸進求解器）的SBR算法，使用個人筆記本（8GHz內存）即可完成電尺寸達200倍波長的縮比艦船模型的散射特性的計算，計算效率可以說相當之高。

階段3：數值方法階段

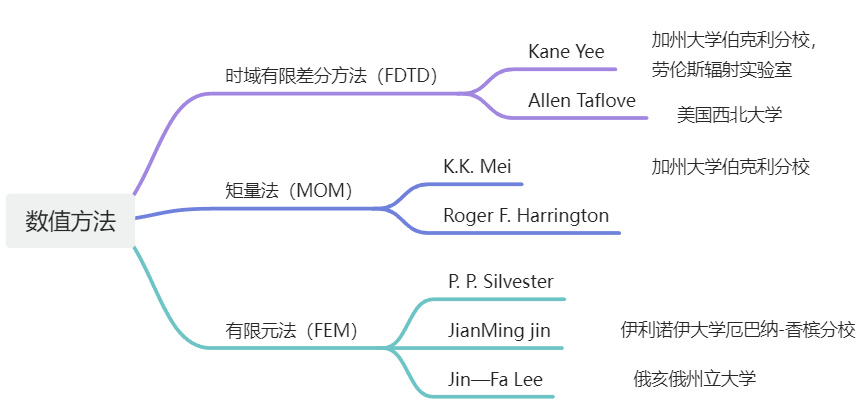
隨著電子計算機“ENIAC”的誕生以及其后“計算能力”飛速發展，基于“數值計算”的全波分析方法也迎來了爆發式發展。其中要以時域有限差分算法（FDTD），有限元算法（FEM）以及矩量法（MOM）發展最為完備，成為三種最主流的電磁數值計算方法。

FDTD（時域有限差分）：

1966年，加州大學伯克利分校的Kane S. Yee教授發表了基于交替網格的有限差分求解Maxwell方程的論文，1980年，該方法正是被命名為FDTD，全文的被被引用次數高達8000次。其離散的對象直接是時域微分形式的Maxwell方程組:

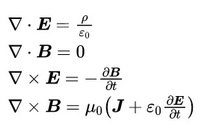
FDTD所使用離散形式也是最為簡單的立方體網格，每一個立方體網格就是一個Yee元胞。

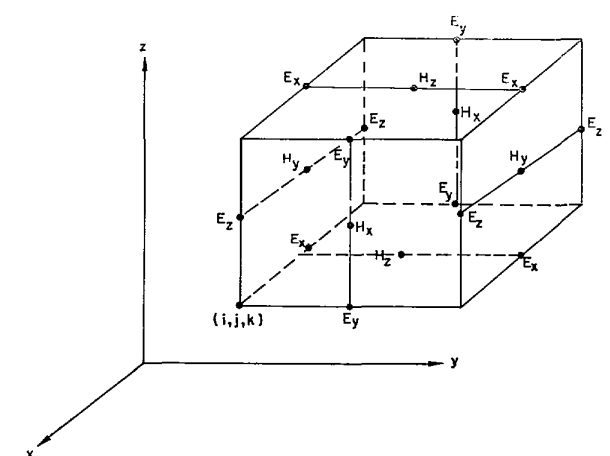
每個元胞上的電場和磁場可以分解為直角坐標系下的三方向分量、、以及、、，上述矢量形式的Maxwell方程即可以展開為標量形式的maxwell方程：

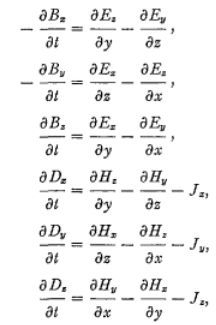
由標量形式方程可知，方程中包含了對電場和磁場分布函數的時間微分運算以及空間微分運算，以電場為例，其中表示對時間的微分運算，和表示對空間的微分運算，其中和最終均可以拆解為，，的組合，這四種微分運算可以用這種通用的表達式進行描述，其可近似為一種簡單差分形式：

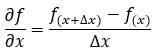
利用這個近似運算，可以將電場對時間的微分運算轉換成前一時刻的電場與后一時刻電場之間的運算關系。同樣地電場E對空間微分運算轉換成前一位置處的電場與后一位置處的電場之間的運算關系 ，因而只要給定了電磁場的初始值和(初始條件)以及邊界值和（邊界條件），即可以基于差分關系式，通過不斷的循環迭代，求解出任意時刻，任意位置處的電磁場分布和和。

MOM（矩量法）：

矩量法的的基本數學概念最初在20世紀初被提出，直到20世紀60年代中期，隨著K. K. Mei教授等研究人員將其引電磁學的數值計算，才逐漸被大家廣泛關注，1968年，Harrintong教授在其開創性的專著《Field Computation by Moment Methods》中對矩量法進行了統一闡述。此后，矩量法得到進一步發展，并被廣泛用于求解各類重要的電磁問題。

FDTD和FEM的統治方程均基于微分形式的Maxwell方程，其特點為：1）其通過直接求解“場”（電場或磁場）滿足的方程來獲得空間電磁場的分布；2）求解對象為“微分形式”的Maxwell方程。而MoM則基于一種完全不同的求解思路。

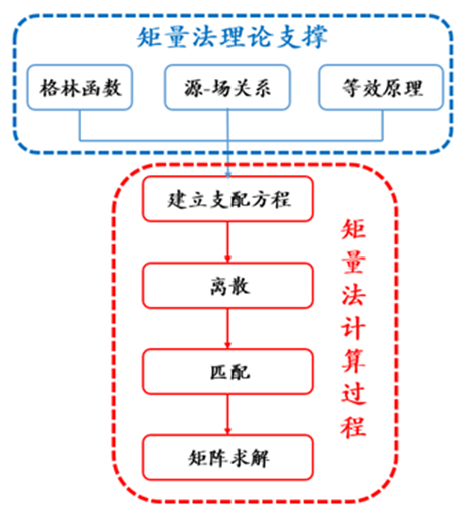
MoM算法理論主要分為兩個部分：一個是矩量法支撐理論，主要包括“格林函數”，“源-場關系”，“等效原理”三個子理論，它們是MoM算法如此特立獨行的根本原因；另一個則是矩量法計算理論，主要包括四個步驟：建立支配方程—>離散—>匹配—>矩陣求解，這與FEM或FDTD算法的求解過程并無明顯區別。詳細的推理過程，作者在往期文章“CAE設計師的你，有必要了解計算電磁學嗎？”中已做了詳盡展示，此處就不在贅述。

FEM（有限元）：

1969年，P. P. Silvester使用有限元方法分析了空心波導中波的傳播，這是有限元方法第一次被應用于微波工程和電磁學中。

有限元法基于頻域Maxwell方程，其求解的對象是時諧電磁場，即電磁場在時間維度上是周期性分布，循環往復，無始無終，時間變量自然也就失去了意義，電磁場只是空間變量的分布函數：

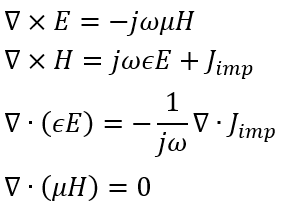
其采用了擬合效果更好的四面體網格對求解區域體進行剖分。

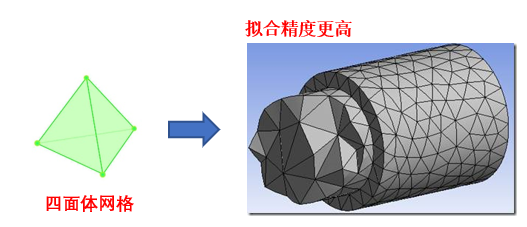
求解空間離散后，緊接著是要空間中待求解的電磁場分布進行離散，其核心思想在于尋找到一組展開未知解的基函數：

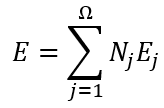
其中為第j條棱邊的切向分量，為待求的切向分量，而為相應棱邊上對應的基函數，一旦將所有未知量求解出來，則整個空間中電場分布就完成了求解。這類似于傅里葉級數中使用三角函數展開任意形式的周期函數，所要做的就是求解每個基函數前面系數，然而對于形狀不規則的電磁問題，這種基函數的尋找是及其困難甚至不可能的，有限元法的做法是將目標離散成小的單元（三角形，四面體），然后使用非常簡單的線性函數或二次函數來近似這個單元上的未知解，這些簡單的基函數是一種子域基函數，其與上文中傅里葉級數展開中的全局基函數有著很大的不同。利用有限元將目標離散，并依據電場E在空間Ω滿足的波動方程和在邊界Γ上滿足的邊界條件條件建立子域基函數的系數所滿足的方程組：

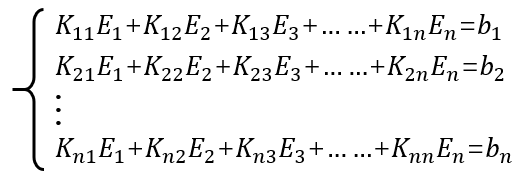
該方程未知量為子域基函數的系數，完成所有未知量的求解，整個空間的電場分布既可以表示為子域函數的疊加。

階段4：快速計算

傳統的數值方法（FEM/FDTD/MOM等）精度高，但對于復雜電大尺寸目標，離散需要的未知量數目多，計算存儲巨大，效率低。高頻近似方法（GO/GTD/UTD/PO/PTD等）存儲量要求低，計算速度快，但是精度難以滿足要求。

尋求精確、高效的數值建模方法是計算電磁學領域高度關注的重要課題，直到世紀之交，快速算法的的出現以及后面的迅猛發展，大大降低了計算的復雜度和存儲量。由于胡俊教授所在的電子科大電磁輻射/散射研究團隊研究重點聚焦于“積分方程方法”，因此大會報告中關于“快速算法”的一些進展主要圍繞“積分方程展開”。積分方程方法的主要特點為：

基于格林函數：自動滿足遠場輻射條件，無需設置吸收邊界條件，沒有網格截斷誤差；

等效電流/磁流作為待求未知量：分布在目標表面（導體/均勻介質）或目標體內（非均勻介質）；

阻抗矩陣元素精確計算難題：奇異性、近奇異性積分數值計算；

全局耦合：不同于微分方程產生的稀疏矩陣，積分方程方法導致稠密矩陣，帶來較高的計算復雜度和存儲量；

快速算法按照求解方法可以分為迭代求解技術和直接求解技術，其中迭代求解技術速度更快但是處理病態矩陣會存在不收斂的問題，直接求解技術不存在收斂性的問題、且適合處理多右端項問題。

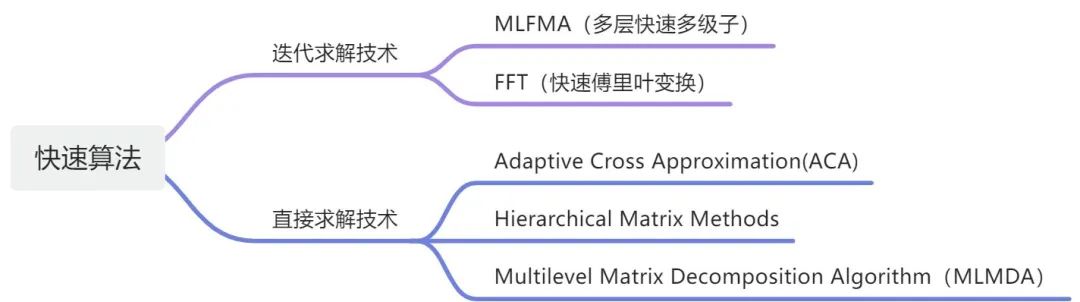
FMM（快速多級子）：

FMM（快速多級子算法）最初由耶魯大學的Rokhlin教授提出，用來快速求解粒子間的相互作用和靜態方程。后來被周永祖（W. C. Chew）教授引入計算電磁學，極大的降低了計算復雜度和內存消耗，其后，國內的聶在平教授帶領的團隊獨立在該領域率先取得突破。

在矩量法中，矩陣向量積的計算可以等效看成計算許多電流元的自作用和互作用，即計算每個電流元所輻射的被所有電流元接收到的場。快速多級子基于這樣的基本思想：首先根據電流元在空間中的位置將其分成若干組，每一組為相互鄰近電流元的集合，然后基于加法定理，將組內不同電流元從不同中心發出的輻射場變換成一個共同中心輻射的場。

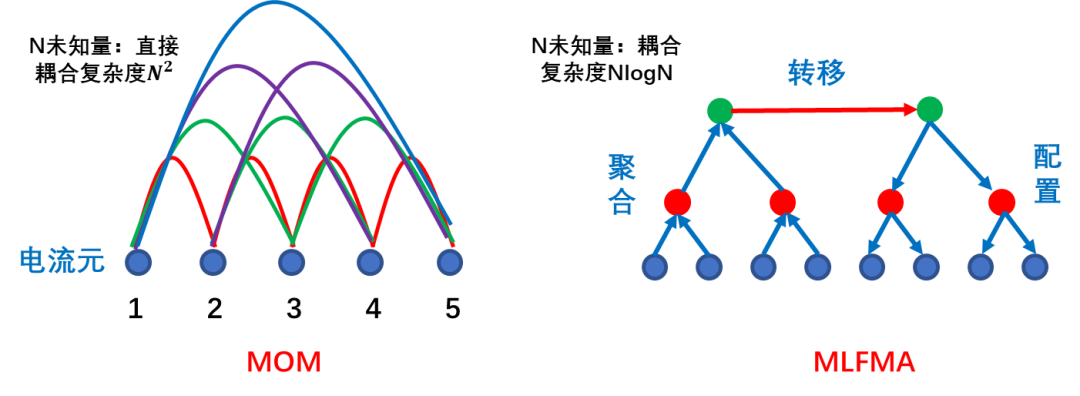
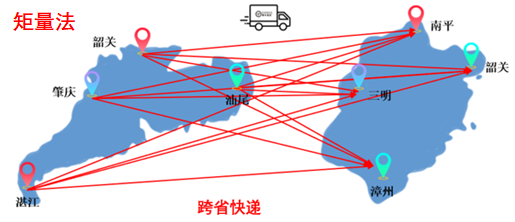
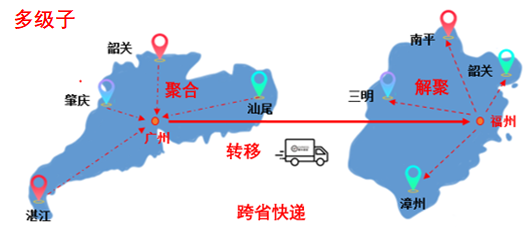
通俗的理解，可以參考往期文章“CAE設計師的你，有必要了解計算電磁學嗎？”中“跨省快遞”的類比，由圖可知：快速多級子算法極大的降低單元之間耦合的計算量。

CG-FFT（共軛梯度-快速傅里葉變換）：

歷史上第一個為計算電磁學開發的快速算法是共軛梯度-快速傅里葉變換法，因為其簡單性，這種方法至今依然是最有效的快速算法。算法的核心思想是將矩量法的矩陣分解成近相互作用和遠相互作用兩個部分，這一思想與后來的快速多級子具有相同的核心思想。

有關共軛梯度-快速傅里葉變換算法（CG-FFT）的更加深入的數理推演，受限于作者目前的認知水平和精力，只能暫時先留下相關學習著作和參考文獻，以備后續深入學習之需要，互勉。

延申：基于積分方程方法的一些最新進展

由于胡俊教授所在的研究團隊主要致力于“積分方程方法”的研究，因此電磁計算目前最前沿的研究“引申”也主要圍繞積分方程方法（IE）展開。

隨著電磁計算方法應用的日益廣泛，所要面對的求解問題也越來越復雜，復雜目標電磁建模面對的困難主要分為以下幾個方面：

目標由介質/金屬組成，多媒質問題；

細微于宏觀結構并存，多尺度問題；

目標電大尺寸/超電大尺寸問題；

散射強度較低（隱身），計算精確性要求高；

多尺度多媒質目標計算的收斂性差；

圍繞這些問題，主要的研究思路有：1）發展區域分解方法；2）發展直接求解器......

DDM（Domain Decomposition Method區域分解算法）

2013年，IEEE Fellow、俄亥俄州立大學教授Jin-Fa Lee的學生Zhen Peng發表了題為《A Discontinuous Galerkin Surface Integral Equation Method for Electromagnetic Wave Scattering From Nonpenetrable Targets》，并于次年獲得“謝昆諾夫最佳論文獎”，帶動了一股積分方程區域分解方法（IE-DDM）的研究潮。

傳統積分方程方法（Integral Equation），如我們在FEKO仿真軟件中使用的矩量法（MOM）或基于其上改進的多層快速多級子算法（MLFMM），由于需要保持剖分網格在棱邊上不會產生電荷積累，因此對網格的要求是一定要共形，即所有的剖分單元都要共邊。這也有就是為什么使用FEKO對相接觸的模型進行剖分時，必須要union，以確保相鄰模型會一體化剖分，維持共形條件。

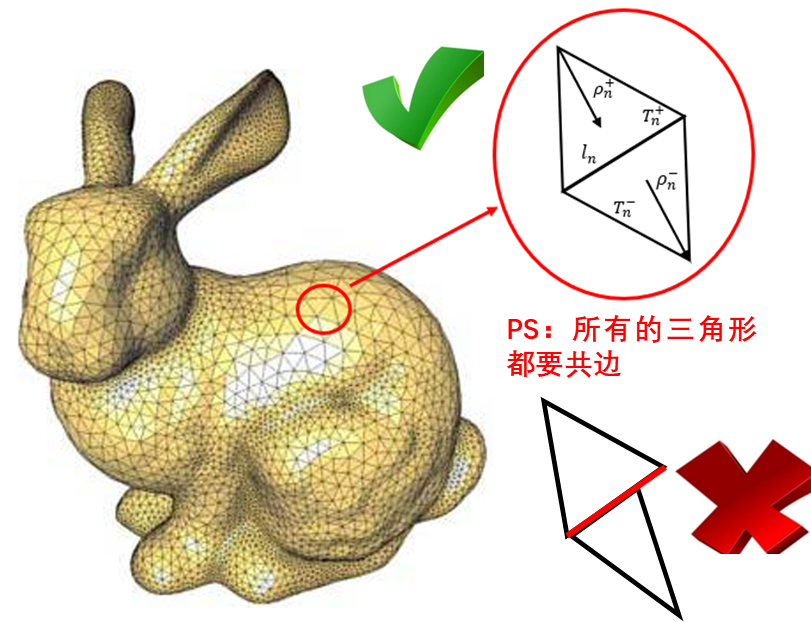
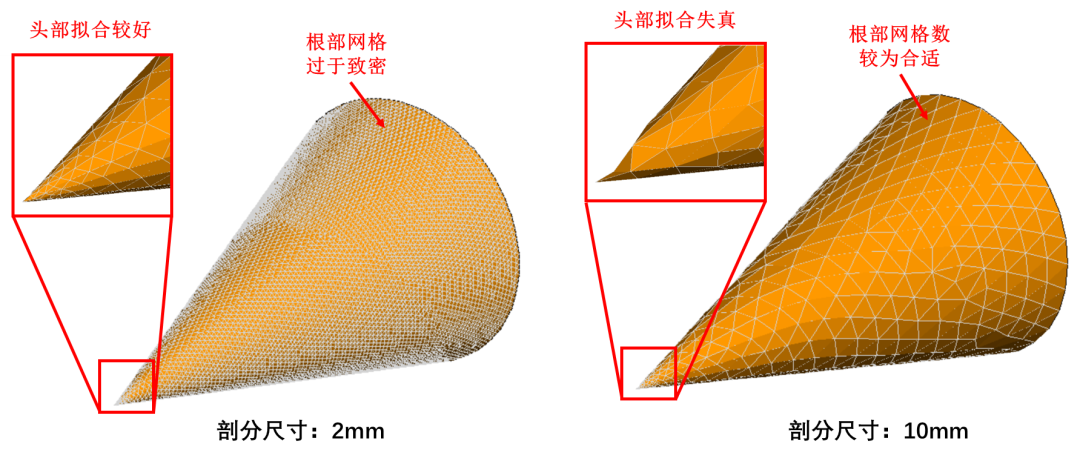
網格共形的要求對于處理一些類似于“多尺度問題”時（同時包含有精細結構和平坦結構），則會遇到較大麻煩：如下圖所示的尖錐模型的剖分示意圖，如果需要較好的擬合頭部（精細結構）形狀，則剖分尺寸較小，根部平坦區域的網格則顯得過于致密，網格數量多，如果按照根部平坦區域去設置剖分尺寸，則網格對于頭部區域的擬合則會出現的失真現象，影響計算精度；同時，網格尺寸在模型表面過快的增長也會帶來矩陣性態的惡化，從而導致收斂性變差的問題。

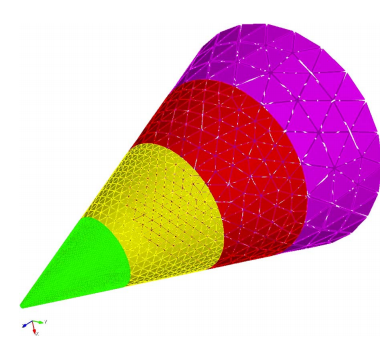
IE-DDM的思想就是按照模型的精細程度進行分類，不同區域按照不同的剖分尺寸進行進行剖分，分別計算，分而治之。其主要克服的難點就在于解決網格不連續處的電荷積累問題，具體的理論推演可以閱讀Zhen Peng的原文，這里就不作展開了。

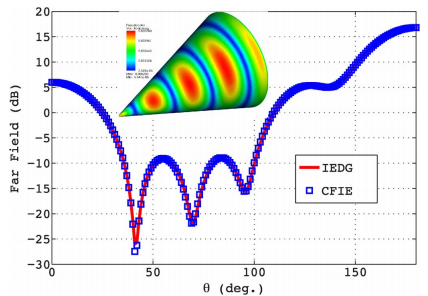
文中，作者挑戰了一個包含天線罩、機載天線、進氣道、掛載武器等多種令積分方程較為頭疼部件的F-16戰斗機整機的的電磁計算問題。分別計算了戰機在3GHz和10GHz頻率下的表面電流分布。

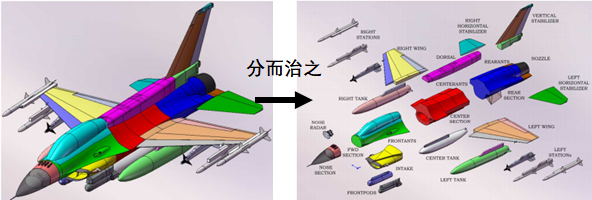
Directive solver（直接求解方法）

圍繞著“積分方程”方法，發展了兩種求解思路，一種類似于上文中所提到的共軛梯度-快速傅里葉變換算法和快速多級子算法的迭代求解方法。這類方法計算速度快、內存消耗小，針對絕大部分電磁計算問題，不失為最優選擇。但是不太適用于以下情況：

病態矩陣系統（強諧振、多尺度結構）

多右端項問題（單站RCS、不確定性量化）

系統部分更新（逆散射問題、閉環優化）

遇到這些情景時，高效的直接求解算法可能成為更好的選擇。直接求解方法圍繞散射矩陣，直接開展計算，因此不存在收斂的問題，且對于多右端項問題，只需計算一種狀態，其余狀態即可快速給出，因此狀態非常多時，也不失為一個好的選擇。

高效的直接求解算法，則是針對“傳統直接求解算法”矩陣計算速度太慢、內存消耗太大的問題而開展的，一般基于低秩壓縮，主要方法有：

改進型HODLR矩陣方法

增強型Skeletonization方法

Butterfy方法

審核編輯：劉清