海森堡不確定性原理是德國物理學家維爾納·海森堡于1927年提出的,它表明在量子力學里,粒子的位置和動量不可能同時被精確地測量,位置的不確定性和動量的不確定性的乘積必然大于等于普朗克常數除以4π(公式:ΔxΔp≥h/4π)。這意味著,微觀世界的粒子行為與我們熟悉的宏觀物質很不一樣,它們具有一種隨機性和概率性,而不是絕對的確定性和因果性。
那么,海森堡不確定性原理的本質是什么呢?為什么我們不能同時知道一個粒子的位置和動量呢?這與我們的生活有什么關系呢?要回答這些問題,我們需要從兩個方面來理解海森堡不確定性原理:一是測量的角度,二是波函數的角度。
從測量的角度來看,海森堡不確定性原理反映了對于微觀粒子的測量所面臨的固有限制。要測量一個粒子的位置或動量,我們需要用另一個粒子或波來與之相互作用,比如用光子或電子來照射它。但是,這樣做就會不可避免地擾動被測量粒子的運動狀態,從而改變它的位置或動量。
而且,擾動的程度與我們用來測量的粒子或波的能量或波長有關。如果我們想要更精確地測量位置,就需要用更短波長或更高能量的粒子或波來照射它,這樣就會造成更大的擾動,從而使得動量更不確定;反之亦然。因此,位置和動量之間存在著一個無法突破的平衡點。
從波函數的角度來看,海森堡不確定性原理反映了微觀粒子具有波粒二象性的本質特征。在量子力學中,微觀粒子可以用波函數來描述,波函數是一個復數函數,它在位置空間或動量空間中給出了粒子出現在某處或具有某種動量的概率密度。因此,波函數又叫做概率幅。根據波恩的概率解釋,波函數在位置空間中的模方表示了粒子在空間中分布的概率密度;而波函數在動量空間中的模方表示了粒子具有不同動量值的概率密度。
而位置空間中的波函數和動量空間中的波函數之間存在著一個傅里葉變換的關系。這個關系可以用一個定理來表述,即傅里葉變換的不確定性原理,也稱為時間-頻率不確定性原理。這個原理說的是,一個信號不可能同時在頻域和時域具有任意小的分辨率,如果它在時間域上變得越窄,那么它在頻率域上就會變得越寬,反之亦然。
那么,這個傅里葉變換的不確定性原理和海森堡不確定性原理有什么關系呢?事實上它們是等價的,如果我們把傅里葉變換的不確定性原理應用到位置和動量上,就可以得到海森堡不確定性原理。也就是說,海森堡不確定性原理是傅里葉變換的不確定性原理在量子力學中的應用。 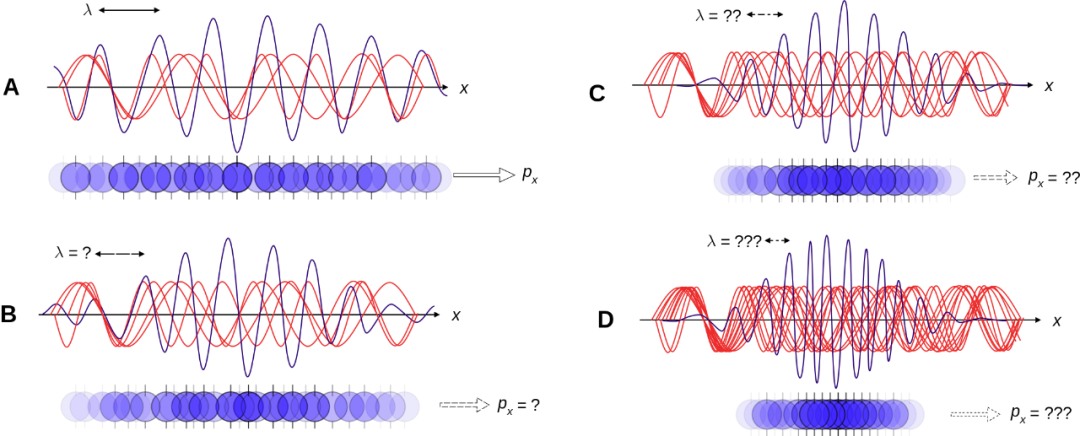 ?
?
那么,海森堡不確定性原理與我們的生活有什么關系呢?其實,在我們日常經驗的尺度上,海森堡不確定性原理是可以忽略的。因為普朗克常數非常小(約為6.626×10^-34 J·s),所以位置和動量的不確定性也非常小。這意味著,在宏觀世界中,我們可以同時知道一個物體的位置和動量,并且可以用牛頓力學來描述它們之間的因果關系。
但是,在微觀世界中,海森堡不確定性原理就不能忽略了。因為微觀粒子的質量和速度都非常小,所以位置和動量的不確定性就相對較大。這意味著,在微觀世界中,我們不能同時知道一個粒子的位置和動量,并且不能用牛頓力學來描述它們之間的因果關系。而這就給我們對微觀現象的認識帶來了機遇與挑戰。
例如,微觀世界的不確定性導致了隧道效應,即一個粒子可以以一定的概率穿越一個本來無法越過的勢壘。這個效應在核物理、半導體、超導等領域有重要的應用。微觀世界的不確定性導致了量子漲落,即真空中會不斷地產生和湮滅一對正負虛粒子。這個效應在宇宙學、黑洞物理、粒子物理等領域有重要的應用。
審核編輯:劉清
-
傅里葉變換
+關注
關注
6文章
426瀏覽量
42479 -
小波函數
+關注
關注
0文章
2瀏覽量
4831
原文標題:從測量和波函數角度理解海森堡不確定性原理
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
計及多重不確定性的規模化電動汽車接入配電網調度方法及解決方案
相對于人工的不確定性,機器人碼垛有何優勢
海能達起訴美國法院產品禁售令被暫停
海信馬曉龍:堅定長期主義的戰略定力,激發“確定性”增長的內生動力

上海交大科研團隊使用Moku:pro推進在量子光學實驗中的多參數估計

確定性網絡技術如何提高網絡的可靠性?

智能制造的本質是解決不確定性
三星電子急簽WOLED訂單:為應對LCD供應不確定性
消除熱電偶溫度測量中的不確定性(使用AD594/AD595)

限制阻抗控制性能優化的因素是什么
大規模確定性網絡技術分析與展望
鴻海10月營收同比下滑4.56% 發展面臨不確定性
如何實施時間敏感型網絡以確保確定性通信




 海森堡不確定性原理的本質是什么呢?
海森堡不確定性原理的本質是什么呢?











評論