這是好久之前的一篇文章學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)的框架思維的修訂版。之前那篇文章收到廣泛好評,沒看過也沒關(guān)系,這篇文章會涵蓋之前的所有內(nèi)容,并且會舉很多代碼的實例,談?wù)勅绾问褂每蚣芩季S,并且給對于算法無從下手的朋友給一點具體可執(zhí)行的刷題建議。
首先,這里講的都是普通的數(shù)據(jù)結(jié)構(gòu)和算法,咱不是搞競賽的,野路子出生,只解決常規(guī)的問題,以面試為最終目標(biāo)。另外,以下是我個人的經(jīng)驗的總結(jié),沒有哪本算法書會寫這些東西,所以請讀者試著理解我的角度,別糾結(jié)于細(xì)節(jié)問題,因為這篇文章就是對數(shù)據(jù)結(jié)構(gòu)和算法建立一個框架性的認(rèn)識。
從整體到細(xì)節(jié),自頂向下,從抽象到具體的框架思維是通用的,不只是學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)和算法,學(xué)習(xí)其他任何知識都是高效的。
先說數(shù)據(jù)結(jié)構(gòu),然后再說算法。
一、數(shù)據(jù)結(jié)構(gòu)的存儲方式
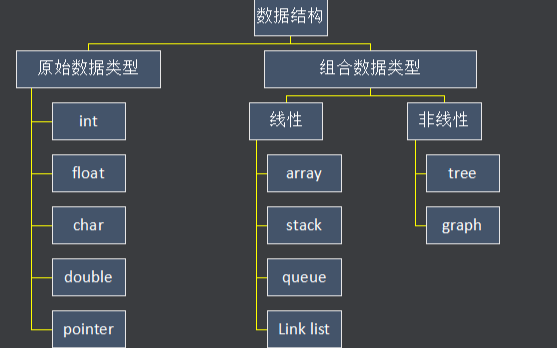
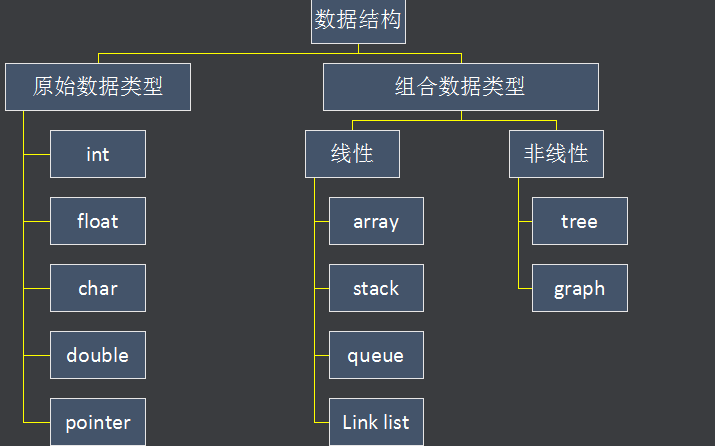
數(shù)據(jù)結(jié)構(gòu)的存儲方式只有兩種: 數(shù)組(順序存儲)和鏈表(鏈?zhǔn)酱鎯Γ?/strong> 。
這句話怎么理解,不是還有散列表、棧、隊列、堆、樹、圖等等各種數(shù)據(jù)結(jié)構(gòu)嗎?
我們分析問題,一定要有遞歸的思想,自頂向下,從抽象到具體。你上來就列出這么多,那些都屬于「上層建筑」,而數(shù)組和鏈表才是「結(jié)構(gòu)基礎(chǔ)」。因為那些多樣化的數(shù)據(jù)結(jié)構(gòu),究其源頭,都是在鏈表或者數(shù)組上的特殊操作,API 不同而已。
比如說 「隊列 」 、 「棧」 這兩種數(shù)據(jù)結(jié)構(gòu)既可以使用鏈表也可以使用數(shù)組實現(xiàn)。用數(shù)組實現(xiàn),就要處理擴(kuò)容縮容的問題;用鏈表實現(xiàn),沒有這個問題,但需要更多的內(nèi)存空間存儲節(jié)點指針。
「圖」 的兩種表示方法,鄰接表就是鏈表,鄰接矩陣就是二維數(shù)組。鄰接矩陣判斷連通性迅速,并可以進(jìn)行矩陣運算解決一些問題,但是如果圖比較稀疏的話很耗費空間。鄰接表比較節(jié)省空間,但是很多操作的效率上肯定比不過鄰接矩陣。
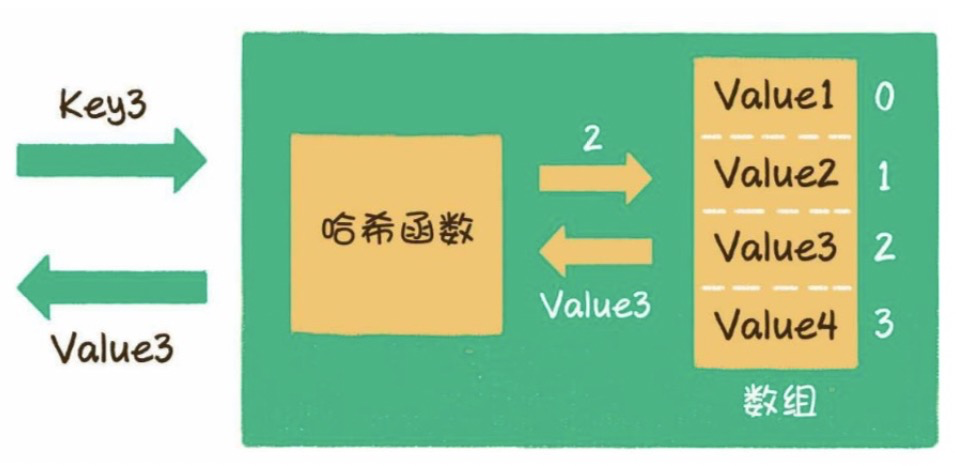
「散列表」 就是通過散列函數(shù)把鍵映射到一個大數(shù)組里。而且對于解決散列沖突的方法,拉鏈法需要鏈表特性,操作簡單,但需要額外的空間存儲指針;線性探查法就需要數(shù)組特性,以便連續(xù)尋址,不需要指針的存儲空間,但操作稍微復(fù)雜些。
「樹」 ,用數(shù)組實現(xiàn)就是「堆」,因為「堆」是一個完全二叉樹,用數(shù)組存儲不需要節(jié)點指針,操作也比較簡單;用鏈表實現(xiàn)就是很常見的那種「樹」,因為不一定是完全二叉樹,所以不適合用數(shù)組存儲。為此,在這種鏈表「樹」結(jié)構(gòu)之上,又衍生出各種巧妙的設(shè)計,比如二叉搜索樹、AVL 樹、紅黑樹、區(qū)間樹、B 樹等等,以應(yīng)對不同的問題。
了解 Redis 數(shù)據(jù)庫的朋友可能也知道,Redis 提供列表、字符串、集合等等幾種常用數(shù)據(jù)結(jié)構(gòu),但是對于每種數(shù)據(jù)結(jié)構(gòu),底層的存儲方式都至少有兩種,以便于根據(jù)存儲數(shù)據(jù)的實際情況使用合適的存儲方式。
綜上,數(shù)據(jù)結(jié)構(gòu)種類很多,甚至你也可以發(fā)明自己的數(shù)據(jù)結(jié)構(gòu),但是底層存儲無非數(shù)組或者鏈表, 二者的優(yōu)缺點如下 :
數(shù)組由于是緊湊連續(xù)存儲,可以隨機(jī)訪問,通過索引快速找到對應(yīng)元素,而且相對節(jié)約存儲空間。但正因為連續(xù)存儲,內(nèi)存空間必須一次性分配夠,所以說數(shù)組如果要擴(kuò)容,需要重新分配一塊更大的空間,再把數(shù)據(jù)全部復(fù)制過去,時間復(fù)雜度 O(N);而且你如果想在數(shù)組中間進(jìn)行插入和刪除,每次必須搬移后面的所有數(shù)據(jù)以保持連續(xù),時間復(fù)雜度 O(N)。
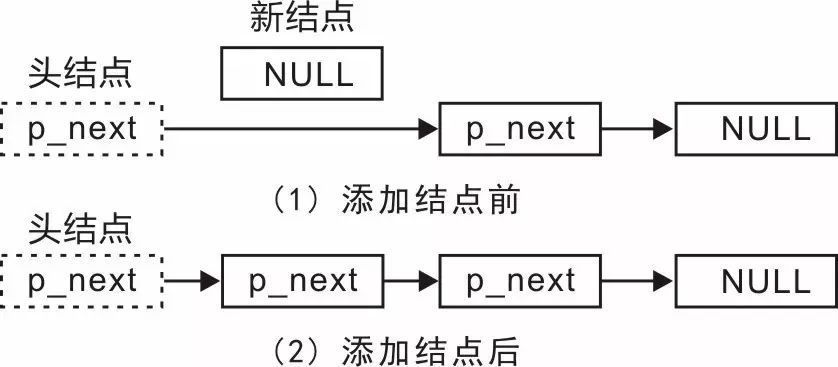
鏈表因為元素不連續(xù),而是靠指針指向下一個元素的位置,所以不存在數(shù)組的擴(kuò)容問題;如果知道某一元素的前驅(qū)和后驅(qū),操作指針即可刪除該元素或者插入新元素,時間復(fù)雜度 O(1)。但是正因為存儲空間不連續(xù),你無法根據(jù)一個索引算出對應(yīng)元素的地址,所以不能隨機(jī)訪問;而且由于每個元素必須存儲指向前后元素位置的指針,會消耗相對更多的儲存空間。
二、數(shù)據(jù)結(jié)構(gòu)的基本操作
對于任何數(shù)據(jù)結(jié)構(gòu),其基本操作無非遍歷 + 訪問,再具體一點就是:增刪查改。
數(shù)據(jù)結(jié)構(gòu)種類很多,但它們存在的目的都是在不同的應(yīng)用場景,盡可能高效地增刪查改 。話說這不就是數(shù)據(jù)結(jié)構(gòu)的使命么?
如何遍歷 + 訪問?我們?nèi)匀粡淖罡邔觼砜矗鞣N數(shù)據(jù)結(jié)構(gòu)的遍歷 + 訪問無非兩種形式:線性的和非線性的。
線性就是 for/while 迭代為代表,非線性就是遞歸為代表。再具體一步,無非以下幾種框架:
數(shù)組遍歷框架,典型的線性迭代結(jié)構(gòu):
void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
// 迭代訪問 arr[i]
}
}
鏈表遍歷框架,兼具迭代和遞歸結(jié)構(gòu):
/* 基本的單鏈表節(jié)點 */
class ListNode {
int val;
ListNode next;
}
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
// 迭代訪問 p.val
}
}
void traverse(ListNode head) {
// 遞歸訪問 head.val
traverse(head.next)
}
二叉樹遍歷框架,典型的非線性遞歸遍歷結(jié)構(gòu):
/* 基本的二叉樹節(jié)點 */
class TreeNode {
int val;
TreeNode left, right;
}
void traverse(TreeNode root) {
traverse(root.left)
traverse(root.right)
}
你看二叉樹的遞歸遍歷方式和鏈表的遞歸遍歷方式,相似不?再看看二叉樹結(jié)構(gòu)和單鏈表結(jié)構(gòu),相似不?如果再多幾條叉,N 叉樹你會不會遍歷?
二叉樹框架可以擴(kuò)展為 N 叉樹的遍歷框架:
/* 基本的 N 叉樹節(jié)點 */
class TreeNode {
int val;
TreeNode[] children;
}
void traverse(TreeNode root) {
for (TreeNode child : root.children)
traverse(child)
}
N 叉樹的遍歷又可以擴(kuò)展為圖的遍歷,因為圖就是好幾 N 叉棵樹的結(jié)合體。你說圖是可能出現(xiàn)環(huán)的?這個很好辦,用個布爾數(shù)組 visited 做標(biāo)記就行了,這里就不寫代碼了。
所謂框架,就是套路。不管增刪查改,這些代碼都是永遠(yuǎn)無法脫離的結(jié)構(gòu),你可以把這個結(jié)構(gòu)作為大綱,根據(jù)具體問題在框架上添加代碼就行了,下面會具體舉例 。
-
算法
+關(guān)注
關(guān)注
23文章
4599瀏覽量
92643 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40093 -
數(shù)組
+關(guān)注
關(guān)注
1文章
415瀏覽量
25908
發(fā)布評論請先 登錄
相關(guān)推薦
數(shù)據(jù)結(jié)構(gòu)與算法分析(Java版)(pdf)
請問學(xué)習(xí)stm32以及ucos ii ucgui需要學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)算法之類的知識嗎?
數(shù)據(jù)結(jié)構(gòu)教程,下載
數(shù)據(jù)結(jié)構(gòu)與算法習(xí)題
數(shù)據(jù)結(jié)構(gòu)與算法
java數(shù)據(jù)結(jié)構(gòu)學(xué)習(xí)
為什么要學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)?數(shù)據(jù)結(jié)構(gòu)的應(yīng)用詳細(xì)資料概述免費下載
什么是數(shù)據(jù)結(jié)構(gòu)?為什么要學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)?數(shù)據(jù)結(jié)構(gòu)的應(yīng)用實例分析
大牛分享平時如何學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)與算法
JavaScrit數(shù)據(jù)結(jié)構(gòu)與算法(第2版)
數(shù)據(jù)結(jié)構(gòu)和算法學(xué)習(xí)筆記(2)
算法和數(shù)據(jù)結(jié)構(gòu)基礎(chǔ)知識分享(中)




 數(shù)據(jù)結(jié)構(gòu)和算法學(xué)習(xí)筆記(1)
數(shù)據(jù)結(jié)構(gòu)和算法學(xué)習(xí)筆記(1)










評論