第一部分 什么是卷積，卷積有什么用，什么是傅利葉變換，什么是拉普拉斯變換?

引子

很多朋友和我一樣，工科電子類專業(yè)，學(xué)了一堆信號(hào)方面的課，什么都沒學(xué)懂，背了公式考了試，然后畢業(yè)了。

先說"卷積有什么用"這個(gè)問題。(有人搶答，"卷積"是為了學(xué)習(xí)"信號(hào)與系統(tǒng)"這門課的后續(xù)章節(jié)而存在的。我大吼一聲，把他拖出去槍斃!)

講一個(gè)故事:

張三剛剛應(yīng)聘到了一個(gè)電子產(chǎn)品公司做測(cè)試人員，他沒有學(xué)過"信號(hào)與系統(tǒng)"這門課程。一天，他拿到了一個(gè)產(chǎn)品，開發(fā)人員告訴他，產(chǎn)品有一個(gè)輸入端，有一個(gè)輸出端，有限的輸入信號(hào)只會(huì)產(chǎn)生有限的輸出。

然后，經(jīng)理讓張三測(cè)試當(dāng)輸入sin(t)(t<1秒)信號(hào)的時(shí)候(有信號(hào)發(fā)生器)，該產(chǎn)品輸出什么樣的波形。張三照做了，花了一個(gè)波形圖。

"很好!"經(jīng)理說。然后經(jīng)理給了張三一疊A4紙:"這里有幾千種信號(hào)，都用公式說明了，輸入信號(hào)的持續(xù)時(shí)間也是確定的。你分別測(cè)試以下我們產(chǎn)品的輸出波形是什么吧!"

這下張三懵了，他在心理想"上帝，幫幫我把，我怎么畫出這些波形圖呢?"

于是上帝出現(xiàn)了:"張三，你只要做一次測(cè)試，就能用數(shù)學(xué)的方法，畫出所有輸入波形對(duì)應(yīng)的輸出波形"。

上帝接著說:"給產(chǎn)品一個(gè)脈沖信號(hào)，能量是1焦耳，輸出的波形圖畫出來!"

張三照辦了，"然后呢?"

上帝又說，"對(duì)于某個(gè)輸入波形，你想象把它微分成無數(shù)個(gè)小的脈沖，輸入給產(chǎn)品，疊加出來的結(jié)果就是你的輸出波形。你可以想象這些小脈沖排著隊(duì)進(jìn)入你的產(chǎn)品，每個(gè)產(chǎn)生一個(gè)小的輸出，你畫出時(shí)序圖的時(shí)候，輸入信號(hào)的波形好像是反過來進(jìn)入系統(tǒng)的。"

張三領(lǐng)悟了:"哦，輸出的結(jié)果就積分出來啦!感謝上帝。這個(gè)方法叫什么名字呢?"

上帝說:"叫卷積!"

從此，張三的工作輕松多了。每次經(jīng)理讓他測(cè)試一些信號(hào)的輸出結(jié)果，張三都只需要在A4紙上做微積分就是提交任務(wù)了!

張三愉快地工作著，直到有一天，平靜的生活被打破。

經(jīng)理拿來了一個(gè)小的電子設(shè)備，接到示波器上面，對(duì)張三說:"看，這個(gè)小設(shè)備產(chǎn)生的波形根本沒法用一個(gè)簡單的函數(shù)來說明，而且，它連續(xù)不斷的發(fā)出信號(hào)!不過幸好，這個(gè)連續(xù)信號(hào)是每隔一段時(shí)間就重復(fù)一次的。張三，你來測(cè)試以下，連到我們的設(shè)備上，會(huì)產(chǎn)生什么輸出波形!"

張三擺擺手:"輸入信號(hào)是無限時(shí)長的，難道我要測(cè)試無限長的時(shí)間才能得到一個(gè)穩(wěn)定的，重復(fù)的波形輸出嗎?"

經(jīng)理怒了:"反正你給我搞定，否則炒魷魚!"

張三心想:"這次輸入信號(hào)連公式都給出出來，一個(gè)很混亂的波形;時(shí)間又是無限長的，卷積也不行了，怎么辦呢?"

及時(shí)地，上帝又出現(xiàn)了:"把混亂的時(shí)間域信號(hào)映射到另外一個(gè)數(shù)學(xué)域上面，計(jì)算完成以后再映射回來"

"宇宙的每一個(gè)原子都在旋轉(zhuǎn)和震蕩，你可以把時(shí)間信號(hào)看成若干個(gè)震蕩疊加的效果，也就是若干個(gè)可以確定的，有固定頻率特性的東西。"

"我給你一個(gè)數(shù)學(xué)函數(shù)f，時(shí)間域無限的輸入信號(hào)在f域有限的。時(shí)間域波形混亂的輸入信號(hào)在f域是整齊的容易看清楚的。這樣你就可以計(jì)算了"

"同時(shí)，時(shí)間域的卷積在f域是簡單的相乘關(guān)系，我可以證明給你看看"

"計(jì)算完有限的程序以后，取f(-1)反變換回時(shí)間域，你就得到了一個(gè)輸出波形，剩下的就是你的數(shù)學(xué)計(jì)算了!"

張三謝過了上帝，保住了他的工作。后來他知道了，f域的變換有一個(gè)名字，叫做傅利葉，什么什么......

再后來，公司開發(fā)了一種新的電子產(chǎn)品，輸出信號(hào)是無限時(shí)間長度的。這次，張三開始學(xué)拉普拉斯了......

后記:

不是我們學(xué)的不好，是因?yàn)榻滩牟缓茫蠋熤v的也不好。

很欣賞Google的面試題:用3句話像老太太講清楚什么是數(shù)據(jù)庫。這樣的命題非常好，因?yàn)闆]有深入的理解一個(gè)命題，沒有仔細(xì)的思考一個(gè)東西的設(shè)計(jì)哲學(xué)，我們就會(huì)陷入細(xì)節(jié)的泥沼:背公式，數(shù)學(xué)推導(dǎo)，積分，做題;而沒有時(shí)間來回答"為什么要這樣"。做大學(xué)老師的做不到"把厚書讀薄"這一點(diǎn)，講不出哲學(xué)層面的道理，一味背書和翻講ppt，做著枯燥的數(shù)學(xué)證明，然后責(zé)怪"現(xiàn)在的學(xué)生一代不如一代"，有什么意義嗎?

第二部分 到底什么是頻率，什么是系統(tǒng)?

這一篇，我展開的說一下傅立葉變換F。注意，傅立葉變換的名字F可以表示頻率的概念(freqence)，也可以包括其他任何概念，因?yàn)樗皇且粋€(gè)概念模型，為了解決計(jì)算的問題而構(gòu)造出來的(例如時(shí)域無限長的輸入信號(hào)，怎么得到輸出信號(hào))。我們把傅立葉變換看一個(gè)C語言的函數(shù)，信號(hào)的輸出輸出問題看為IO的問題，然后任何難以求解的x->y的問題都可以用x->f(x)->f-1(x)->y來得到。

1、到底什么是頻率?

一個(gè)基本的假設(shè):任何信息都具有頻率方面的特性，音頻信號(hào)的聲音高低，光的頻譜，電子震蕩的周期，等等，我們抽象出一個(gè)件諧振動(dòng)的概念，數(shù)學(xué)名稱就叫做頻率。想象在x-y平面上有一個(gè)原子圍繞原點(diǎn)做半徑為1勻速圓周運(yùn)動(dòng)，把x軸想象成時(shí)間，那么該圓周運(yùn)動(dòng)在y軸上的投影就是一個(gè)sin(t)的波形。相信中學(xué)生都能理解這個(gè)。

那么，不同的頻率模型其實(shí)就對(duì)應(yīng)了不同的圓周運(yùn)動(dòng)速度。圓周運(yùn)動(dòng)的速度越快，sin(t)的波形越窄。頻率的縮放有兩種模式

(a)老式的收音機(jī)都是用磁帶作為音樂介質(zhì)的，當(dāng)我們快放的時(shí)候，我們會(huì)感覺歌唱的聲音變得怪怪的，調(diào)子很高，那是因?yàn)?圓周運(yùn)動(dòng)"的速度增倍了，每一個(gè)聲音分量的sin(t)輸出變成了sin(nt)。

(b)在CD/計(jì)算機(jī)上面快放或滿放感覺歌手快唱或者慢唱，不會(huì)出現(xiàn)音調(diào)變高的現(xiàn)象：因?yàn)榭旆诺臅r(shí)候采用了時(shí)域采樣的方法，丟棄了一些波形，但是承載了信息的輸出波形不會(huì)有寬窄的變化;滿放時(shí)相反，時(shí)域信號(hào)填充拉長就可以了。

2、F變換得到的結(jié)果有負(fù)數(shù)/復(fù)數(shù)部分，有什么物理意義嗎?

解釋:F變換是個(gè)數(shù)學(xué)工具，不具有直接的物理意義，負(fù)數(shù)/復(fù)數(shù)的存在只是為了計(jì)算的完整性。

3、信號(hào)與系統(tǒng)這們課的基本主旨是什么?

對(duì)于通信和電子類的學(xué)生來說，很多情況下我們的工作是設(shè)計(jì)或者OSI七層模型當(dāng)中的物理層技術(shù)，這種技術(shù)的復(fù)雜性首先在于你必須確立傳輸介質(zhì)的電氣特性，通常不同傳輸介質(zhì)對(duì)于不同頻率段的信號(hào)有不同的處理能力。以太網(wǎng)線處理基帶信號(hào)，廣域網(wǎng)光線傳出高頻調(diào)制信號(hào)，移動(dòng)通信，2G和3G分別需要有不同的載頻特性。那么這些介質(zhì)(空氣，電線，光纖等)對(duì)于某種頻率的輸入是否能夠在傳輸了一定的距離之后得到基本不變的輸入呢?那么我們就要建立介質(zhì)的頻率相應(yīng)數(shù)學(xué)模型。同時(shí)，知道了介質(zhì)的頻率特性，如何設(shè)計(jì)在它上面?zhèn)鬏數(shù)男盘?hào)才能大到理論上的最大傳輸速率?----這就是信號(hào)與系統(tǒng)這們課帶領(lǐng)我們進(jìn)入的一個(gè)世界。

當(dāng)然，信號(hào)與系統(tǒng)的應(yīng)用不止這些，和香農(nóng)的信息理論掛鉤，它還可以用于信息處理(聲音，圖像)，模式識(shí)別，智能控制等領(lǐng)域。如果說，計(jì)算機(jī)專業(yè)的課程是數(shù)據(jù)表達(dá)的邏輯模型，那么信號(hào)與系統(tǒng)建立的就是更底層的，代表了某種物理意義的數(shù)學(xué)模型。數(shù)據(jù)結(jié)構(gòu)的知識(shí)能解決邏輯信息的編碼和糾錯(cuò)，而信號(hào)的知識(shí)能幫我們?cè)O(shè)計(jì)出碼流的物理載體(如果接受到的信號(hào)波形是混亂的，那我依據(jù)什么來判斷這個(gè)是1還是0?邏輯上的糾錯(cuò)就失去了意義)。在工業(yè)控制領(lǐng)域，計(jì)算機(jī)的應(yīng)用前提是各種數(shù)模轉(zhuǎn)換，那么各種物理現(xiàn)象產(chǎn)生的連續(xù)模擬信號(hào)(溫度，電阻，大小，壓力，速度等)如何被一個(gè)特定設(shè)備轉(zhuǎn)換為有意義的數(shù)字信號(hào)，首先我們就要設(shè)計(jì)一個(gè)可用的數(shù)學(xué)轉(zhuǎn)換模型。

4、如何設(shè)計(jì)系統(tǒng)?

設(shè)計(jì)物理上的系統(tǒng)函數(shù)(連續(xù)的或離散的狀態(tài))，有輸入，有輸出，而中間的處理過程和具體的物理實(shí)現(xiàn)相關(guān)，不是這們課關(guān)心的重點(diǎn)(電子電路設(shè)計(jì)?)。信號(hào)與系統(tǒng)歸根到底就是為了特定的需求來設(shè)計(jì)一個(gè)系統(tǒng)函數(shù)。設(shè)計(jì)出系統(tǒng)函數(shù)的前提是把輸入和輸出都用函數(shù)來表示(例如sin(t))。分析的方法就是把一個(gè)復(fù)雜的信號(hào)分解為若干個(gè)簡單的信號(hào)累加，具體的過程就是一大堆微積分的東西，具體的數(shù)**算不是這門課的中心思想。

那么系統(tǒng)有那些種類呢?

(a)按功能分類:調(diào)制解調(diào)(信號(hào)抽樣和重構(gòu))，疊加，濾波，功放，相位調(diào)整，信號(hào)時(shí)鐘同步，負(fù)反饋鎖相環(huán)，以及若干子系統(tǒng)組成的一個(gè)更為復(fù)雜的系統(tǒng)----你可以畫出系統(tǒng)流程圖，是不是很接近編寫程序的邏輯流程圖?確實(shí)在符號(hào)的空間里它們沒有區(qū)別。還有就是離散狀態(tài)的數(shù)字信號(hào)處理(后續(xù)課程)。

(b)按系統(tǒng)類別劃分，無狀態(tài)系統(tǒng)，有限狀態(tài)機(jī)，線性系統(tǒng)等。而物理層的連續(xù)系統(tǒng)函數(shù)，是一種復(fù)雜的線性系統(tǒng)。

5、最好的教材?

符號(hào)系統(tǒng)的核心是集合論，不是微積分，沒有集合論構(gòu)造出來的系統(tǒng)，實(shí)現(xiàn)用到的微積分便毫無意義----你甚至不知道運(yùn)算了半天到底是要作什么。以計(jì)算機(jī)的觀點(diǎn)來學(xué)習(xí)信號(hào)與系統(tǒng)，最好的教材之一就是<>，作者是UCBerkeley的EdwardA.LeeandPravinVaraiya----先定義再實(shí)現(xiàn)，符合人類的思維習(xí)慣。國內(nèi)的教材通篇都是數(shù)學(xué)推導(dǎo)，就是不肯說這些推導(dǎo)是為了什么目的來做的，用來得到什么，建設(shè)什么，防止什么;不去從認(rèn)識(shí)論和需求上討論，通篇都是看不出目的的方**，本末倒置了。

第三部分 抽樣定理是干什么的?

1.舉個(gè)例子，打電話的時(shí)候，電話機(jī)發(fā)出的信號(hào)是PAM脈沖調(diào)幅，在電話線路上傳的不是話音，而是話音通過信道編碼轉(zhuǎn)換后的脈沖序列，在收端恢復(fù)語音波形。那么對(duì)于連續(xù)的說話人語音信號(hào)，如何轉(zhuǎn)化成為一些列脈沖才能保證基本不失真，可以傳輸呢?很明顯，我們想到的就是取樣，每隔M毫秒對(duì)話音采樣一次看看電信號(hào)振幅，把振幅轉(zhuǎn)換為脈沖編碼，傳輸出去，在收端按某種規(guī)則重新生成語言。

那么，問題來了，每M毫秒采樣一次，M多小是足夠的?在收端怎么才能恢復(fù)語言波形呢?

對(duì)于第一個(gè)問題，我們考慮，語音信號(hào)是個(gè)時(shí)間頻率信號(hào)(所以對(duì)應(yīng)的F變換就表示時(shí)間頻率)把語音信號(hào)分解為若干個(gè)不同頻率的單音混合體(周期函數(shù)的復(fù)利葉級(jí)數(shù)展開，非周期的區(qū)間函數(shù)，可以看成補(bǔ)齊以后的周期信號(hào)展開，效果一樣)，對(duì)于最高頻率的信號(hào)分量，如果抽樣方式能否保證恢復(fù)這個(gè)分量，那么其他的低頻率分量也就能通過抽樣的方式使得信息得以保存。如果人的聲音高頻限制在3000Hz，那么高頻分量我們看成sin(3000t)，這個(gè)sin函數(shù)要通過抽樣保存信息，可以看為:對(duì)于一個(gè)周期，波峰采樣一次，波谷采樣一次，也就是采樣頻率是最高頻率分量的2倍(奈奎斯特抽樣定理)，我們就可以通過采樣信號(hào)無損的表示原始的模擬連續(xù)信號(hào)。這兩個(gè)信號(hào)一一對(duì)應(yīng)，互相等價(jià)。

對(duì)于第二個(gè)問題，在收端，怎么從脈沖序列(梳裝波形)恢復(fù)模擬的連續(xù)信號(hào)呢?首先，我們已經(jīng)肯定了在頻率域上面的脈沖序列已經(jīng)包含了全部信息，但是原始信息只在某一個(gè)頻率以下存在，怎么做?我們讓輸入脈沖信號(hào)I通過一個(gè)設(shè)備X，輸出信號(hào)為原始的語音O，那么I(*)X=O，這里(*)表示卷積。時(shí)域的特性不好分析，那么在頻率域F(I)*F(X)=F(O)相乘關(guān)系，這下就很明顯了，只要F(X)是一個(gè)理想的，低通濾波器就可以了(在F域畫出來就是一個(gè)方框)，它在時(shí)間域是一個(gè)鐘型函數(shù)(由于包含時(shí)間軸的負(fù)數(shù)部分，所以實(shí)際中不存在)，做出這樣的一個(gè)信號(hào)處理設(shè)備，我們就可以通過輸入的脈沖序列得到幾乎理想的原始的語音。在實(shí)際應(yīng)用中，我們的抽樣頻率通常是奈奎斯特頻率再多一點(diǎn)，3k赫茲的語音信號(hào)，抽樣標(biāo)準(zhǔn)是8k赫茲。

2.再舉一個(gè)例子，對(duì)于數(shù)字圖像，抽樣定理對(duì)應(yīng)于圖片的分辨率----抽樣密度越大，圖片的分辨率越高，也就越清晰。如果我們的抽樣頻率不夠，信息就會(huì)發(fā)生混疊----網(wǎng)上有一幅圖片，近視眼戴眼鏡看到的是愛因斯坦，摘掉眼睛看到的是夢(mèng)露----因?yàn)椴粠а劬Γ直媛什粔?抽樣頻率太低)，高頻分量失真被混入了低頻分量，才造成了一個(gè)視覺陷阱。在這里，圖像的F變化，對(duì)應(yīng)的是空間頻率。

話說回來了，直接在信道上傳原始語音信號(hào)不好嗎?模擬信號(hào)沒有抗干擾能力，沒有糾錯(cuò)能力，抽樣得到的信號(hào)，有了數(shù)字特性，傳輸性能更佳。

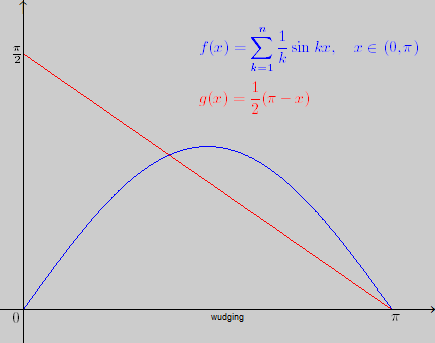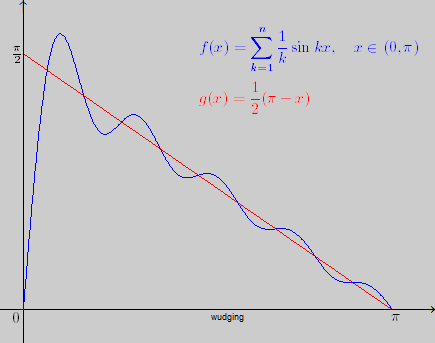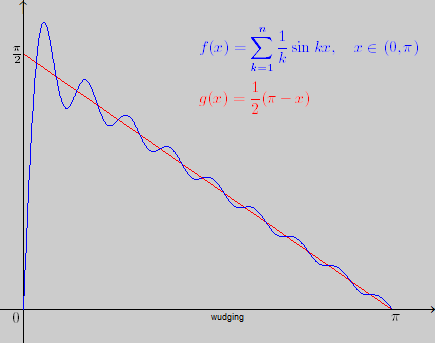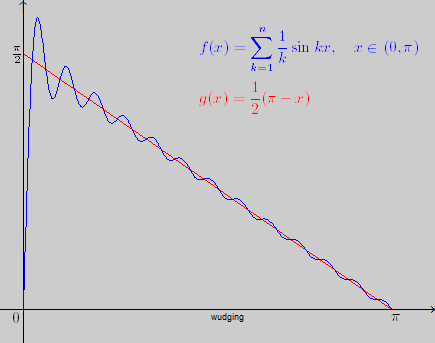
什么信號(hào)不能理想抽樣?時(shí)域有跳變，頻域無窮寬，例如方波信號(hào)。如果用有限帶寬的抽樣信號(hào)表示它，相當(dāng)于復(fù)利葉級(jí)數(shù)取了部分和，而這個(gè)部分和在恢復(fù)原始信號(hào)的時(shí)候，在不可導(dǎo)的點(diǎn)上面會(huì)有毛刺，也叫吉布斯現(xiàn)象。

3.為什么傅立葉想出了這么一個(gè)級(jí)數(shù)來?這個(gè)源于西方哲學(xué)和科學(xué)的基本思想:正交分析方法。例如研究一個(gè)立體形狀，我們使用x,y,z三個(gè)互相正交的軸:任何一個(gè)軸在其他軸上面的投影都是0。這樣的話，一個(gè)物體的3視圖就可以完全表達(dá)它的形狀。同理，信號(hào)怎么分解和分析呢?用互相正交的三角函數(shù)分量的無限和：這就是傅立葉的貢獻(xiàn)。

第四部分 傅立葉變換的復(fù)數(shù)小波

說的廣義一點(diǎn)，"復(fù)數(shù)"是一個(gè)"概念"，不是一種客觀存在。

什么是"概念"?一張紙有幾個(gè)面?兩個(gè)，這里"面"是一個(gè)概念，一個(gè)主觀對(duì)客觀存在的認(rèn)知，就像"大"和"小"的概念一樣，只對(duì)人的意識(shí)有意義，對(duì)客觀存在本身沒有意義(康德:純粹理性的批判)。把紙條的兩邊轉(zhuǎn)一下相連接，變成"莫比烏斯圈"，這個(gè)紙條就只剩下一個(gè)"面"了。概念是對(duì)客觀世界的加工，反映到意識(shí)中的東西。

數(shù)的概念是這樣被推廣的:什么數(shù)x使得x^2=-1?實(shí)數(shù)軸顯然不行，(-1)*(-1)=1。那么如果存在一個(gè)抽象空間，它既包括真實(shí)世界的實(shí)數(shù)，也能包括想象出來的x^2=-1，那么我們稱這個(gè)想象空間為"復(fù)數(shù)域"。那么實(shí)數(shù)的運(yùn)算法則就是復(fù)數(shù)域的一個(gè)特例。為什么1*(-1)=-1?+-符號(hào)在復(fù)數(shù)域里面代表方向，-1就是"向后，轉(zhuǎn)!"這樣的命令，一個(gè)1在圓周運(yùn)動(dòng)180度以后變成了-1，這里，直線的數(shù)軸和圓周旋轉(zhuǎn)，在復(fù)數(shù)的空間里面被統(tǒng)一了。

因此，(-1)*(-1)=1可以解釋為"向后轉(zhuǎn)"+"向后轉(zhuǎn)"=回到原地。那么復(fù)數(shù)域如何表示x^2=-1呢?很簡單，"向左轉(zhuǎn)"，"向左轉(zhuǎn)"兩次相當(dāng)于"向后轉(zhuǎn)"。由于單軸的實(shí)數(shù)域(直線)不包含這樣的元素，所以復(fù)數(shù)域必須由兩個(gè)正交的數(shù)軸表示--平面。很明顯，我們可以得到復(fù)數(shù)域乘法的一個(gè)特性，就是結(jié)果的絕對(duì)值為兩個(gè)復(fù)數(shù)絕對(duì)值相乘，旋轉(zhuǎn)的角度=兩個(gè)復(fù)數(shù)的旋轉(zhuǎn)角度相加。高中時(shí)代我們就學(xué)習(xí)了迪莫弗定理。為什么有這樣的乘法性質(zhì)?不是因?yàn)閺?fù)數(shù)域恰好具有這樣的乘法性質(zhì)(性質(zhì)決定認(rèn)識(shí))，而是發(fā)明復(fù)數(shù)域的人就是根據(jù)這樣的需求去弄出了這么一個(gè)復(fù)數(shù)域(認(rèn)識(shí)決定性質(zhì))，是一種主觀唯心主義的研究方法。為了構(gòu)造x^2=-1，我們必須考慮把乘法看為兩個(gè)元素構(gòu)成的集合:乘積和角度旋轉(zhuǎn)。

因?yàn)槿呛瘮?shù)可以看為圓周運(yùn)動(dòng)的一種投影，所以，在復(fù)數(shù)域，三角函數(shù)和乘法運(yùn)算(指數(shù))被統(tǒng)一了。我們從實(shí)數(shù)域的傅立葉級(jí)數(shù)展開入手，立刻可以得到形式更簡單的，復(fù)數(shù)域的，和實(shí)數(shù)域一一對(duì)應(yīng)的傅立葉復(fù)數(shù)級(jí)數(shù)。因?yàn)閺?fù)數(shù)域形式簡單，所以研究起來方便----雖然自然界不存在復(fù)數(shù)，但是由于和實(shí)數(shù)域的級(jí)數(shù)一一對(duì)應(yīng)，我們做個(gè)反映射就能得到有物理意義的結(jié)果。

那么傅立葉變換，那個(gè)令人難以理解的轉(zhuǎn)換公式是什么含義呢?我們可以看一下它和復(fù)數(shù)域傅立葉級(jí)數(shù)的關(guān)系。什么是微積分，就是先微分，再積分，傅立葉級(jí)數(shù)已經(jīng)作了無限微分了，對(duì)應(yīng)無數(shù)個(gè)離散的頻率分量沖擊信號(hào)的和。傅立葉變換要解決非周期信號(hào)的分析問題，想象這個(gè)非周期信號(hào)也是一個(gè)周期信號(hào):只是周期為無窮大，各頻率分量無窮小而已(否則積分的結(jié)果就是無窮)。那么我們看到傅立葉級(jí)數(shù)，每個(gè)分量常數(shù)的求解過程，積分的區(qū)間就是從T變成了正負(fù)無窮大。而由于每個(gè)頻率分量的常數(shù)無窮小，那么讓每個(gè)分量都去除以f，就得到有值的數(shù)----所以周期函數(shù)的傅立葉變換對(duì)應(yīng)一堆脈沖函數(shù)。同理，各個(gè)頻率分量之間無限的接近，因?yàn)閒很小，級(jí)數(shù)中的f，2f，3f之間幾乎是挨著的，最后挨到了一起，和卷積一樣，這個(gè)復(fù)數(shù)頻率空間的級(jí)數(shù)求和最終可以變成一個(gè)積分式：傅立葉級(jí)數(shù)變成了傅立葉變換。注意有個(gè)概念的變化：離散的頻率，每個(gè)頻率都有一個(gè)"權(quán)"值，而連續(xù)的F域，每個(gè)頻率的加權(quán)值都是無窮小(面積=0)，只有一個(gè)頻率范圍內(nèi)的"頻譜"才對(duì)應(yīng)一定的能量積分。頻率點(diǎn)變成了頻譜的線。

因此傅立葉變換求出來的是一個(gè)通常是一個(gè)連續(xù)函數(shù)，是復(fù)數(shù)頻率域上面的可以畫出圖像的東西?那個(gè)根號(hào)2Pai又是什么?它只是為了保證正變換反變換回來以后，信號(hào)不變。我們可以讓正變換除以2，讓反變換除以Pi，怎么都行。慢點(diǎn)，怎么有"負(fù)數(shù)"的部分，還是那句話，是數(shù)軸的方向?qū)?yīng)復(fù)數(shù)軸的旋轉(zhuǎn)，或者對(duì)應(yīng)三角函數(shù)的相位分量，這樣說就很好理解了。有什么好處?我們忽略相位，只研究"振幅"因素，就能看到實(shí)數(shù)頻率域內(nèi)的頻率特性了。

我們從實(shí)數(shù)(三角函數(shù)分解)->復(fù)數(shù)(e和Pi)->復(fù)數(shù)變換(F)->復(fù)數(shù)反變換(F-1)->復(fù)數(shù)(取幅度分量)->實(shí)數(shù)，看起來很復(fù)雜，但是這個(gè)工具使得，單從實(shí)數(shù)域無法解決的頻率分析問題，變得可以解決了。兩者之間的關(guān)系是:傅立葉級(jí)數(shù)中的頻率幅度分量是a1-an,b1-bn，這些離散的數(shù)表示頻率特性，每個(gè)數(shù)都是積分的結(jié)果。而傅立葉變換的結(jié)果是一個(gè)連續(xù)函數(shù):對(duì)于f域每個(gè)取值點(diǎn)a1-aN(N=無窮)，它的值都是原始的時(shí)域函數(shù)和一個(gè)三角函數(shù)(表示成了復(fù)數(shù))積分的結(jié)果----這個(gè)求解和級(jí)數(shù)的表示形式是一樣的。不過是把N個(gè)離散的積分式子統(tǒng)一為了一個(gè)通用的，連續(xù)的積分式子。

復(fù)頻域，大家都說畫不出來，但是我來畫一下!因?yàn)椴皇且粋€(gè)圖能夠表示清楚的。我用純中文來說:

1.畫一個(gè)x,y軸組成的平面，以原點(diǎn)為中心畫一個(gè)圓(r=1)。再畫一條豎直線:(直線方程x=2)，把它看成是一塊擋板。

2.想象，有一個(gè)原子，從(1,0)點(diǎn)出發(fā)，沿著這個(gè)圓作逆時(shí)針勻速圓周運(yùn)動(dòng)。想象太陽光從x軸的復(fù)數(shù)方向射向x軸的正數(shù)方向，那么這個(gè)原子運(yùn)動(dòng)在擋板(x=2)上面的投影，就是一個(gè)簡協(xié)震動(dòng)。

3.再修改一下，x=2對(duì)應(yīng)的不是一個(gè)擋板，而是一個(gè)打印機(jī)的出紙口，那么，原子運(yùn)動(dòng)的過程就在白紙上畫下了一條連續(xù)的sin(t)曲線!

上面3條說明了什么呢?三角函數(shù)和圓周運(yùn)動(dòng)是一一對(duì)應(yīng)的。如果我想要sin(t+x)，或者cos(t)這種形式，我只需要讓原子的起始位置改變一下就可以了：也就是級(jí)坐標(biāo)的向量，半徑不變，相位改變。

傅立葉級(jí)數(shù)的實(shí)數(shù)展開形式，每一個(gè)頻率分量都表示為AnCos(nt)+BnSin(nt)，我們可以證明，這個(gè)式子可以變成sqr(An^2+Bn^2)sin(nt+x)這樣的單個(gè)三角函數(shù)形式，那么：實(shí)數(shù)值對(duì)(An,Bn)，就對(duì)應(yīng)了二維平面上面的一個(gè)點(diǎn)，相位x對(duì)應(yīng)這個(gè)點(diǎn)的相位。實(shí)數(shù)和復(fù)數(shù)之間的一一對(duì)應(yīng)關(guān)系便建立起來了，因此實(shí)數(shù)頻率唯一對(duì)應(yīng)某個(gè)復(fù)數(shù)頻率，我們就可以用復(fù)數(shù)來方便的研究實(shí)數(shù)的運(yùn)算：把三角運(yùn)算變成指數(shù)和乘法加法運(yùn)算。

但是，F(xiàn)變換仍然是有限制的(輸入函數(shù)的表示必須滿足狄義赫立條件等)，為了更廣泛的使用"域"變換的思想來表示一種"廣義"的頻率信息，我們就發(fā)明出了拉普拉斯變換，它的連續(xù)形式對(duì)應(yīng)F變換，離散形式就成了Z變換。離散信號(hào)呢?離散周期函數(shù)的F級(jí)數(shù)，項(xiàng)數(shù)有限，離散非周期函數(shù)(看為周期延拓以后仍然是離散周期函數(shù))，離散F級(jí)數(shù)，仍然項(xiàng)數(shù)有限。離散的F變換，很容易理解----連續(xù)信號(hào)通過一個(gè)周期采樣濾波器，也就是頻率域和一堆脈沖相乘。時(shí)域取樣對(duì)應(yīng)頻域周期延拓。為什么?反過來容易理解了，時(shí)域的周期延拓對(duì)應(yīng)頻率域的一堆脈沖。

兩者的區(qū)別：FT[f(t)]=從負(fù)無窮到正無窮對(duì)[f(t)exp(-jwt)]積分LT[f(t)]=從零到正無窮對(duì)[f(t)exp(-st)]積分(由于實(shí)際應(yīng)用，通常只做單邊Laplace變換，即積分從零開始)具體地，在Fourier積分變換中，所乘因子為exp(-jwt)，此處，-jwt顯然是為一純虛數(shù);而在laplace變換中，所乘因子為exp(-st)，其中s為一復(fù)數(shù)：s=D+jw,jw是為虛部，相當(dāng)于Fourier變換中的jwt，而D則是實(shí)部，作為衰減因子，這樣就能將許多無法作Fourier變換的函數(shù)(比如exp(at),a>0)做域變換。

而Z變換，簡單地說，就是離散信號(hào)(也可以叫做序列)的Laplace變換，可由抽樣信號(hào)的Laplace變換導(dǎo)出。ZT[f(n)]=從n為負(fù)無窮到正無窮對(duì)[f(n)Z^(-n)]求和。Z域的物理意義:由于值被離散了，所以輸入輸出的過程和花費(fèi)的物理時(shí)間已經(jīng)沒有了必然的關(guān)系(t只對(duì)連續(xù)信號(hào)有意義)，所以頻域的考察變得及其簡單起來，我們把(1,-1,1,-1,1,-1)這樣的基本序列看成是數(shù)字頻率最高的序列，他的數(shù)字頻率是1Hz(數(shù)字角頻率2Pi)，其他的數(shù)字序列頻率都是N分之1Hz，頻率分解的結(jié)果就是0-2Pi角頻率當(dāng)中的若干個(gè)值的集合，也是一堆離散的數(shù)。由于時(shí)頻都是離散的，所以在做變換的時(shí)候，不需要寫出沖擊函數(shù)的因子

離散傅立葉變換到快速傅立葉變換----由于離散傅立葉變換的次數(shù)是O(N^2)，于是我們考慮把離散序列分解成兩兩一組進(jìn)行離散傅立葉變換，變換的計(jì)算復(fù)雜度就下降到了O(NlogN)，再把計(jì)算的結(jié)果累加O(N)，這就大大降低了計(jì)算復(fù)雜度。

再說一個(gè)高級(jí)話題:小波。在實(shí)際的工程應(yīng)用中，前面所說的這些變換大部分都已經(jīng)被小波變換代替了。

什么是小波?先說什么是波：傅立葉級(jí)數(shù)里面的分量，sin/cos函數(shù)就是波，sin(t)/cos(t)經(jīng)過幅度的放縮和頻率的收緊，變成了一系列的波的求和，一致收斂于原始函數(shù)。注意傅立葉級(jí)數(shù)求和的收斂性是對(duì)于整個(gè)數(shù)軸而言的，嚴(yán)格的。不過前面我們說了，實(shí)際應(yīng)用FFT的時(shí)候，我們只需要關(guān)注部分信號(hào)的傅立葉變換然后求出一個(gè)整體和就可以了，那么對(duì)于函數(shù)的部分分量，我們只需要保證這個(gè)用來充當(dāng)磚塊的"波函數(shù)"，在某個(gè)區(qū)間(用窗函數(shù)來濾波)內(nèi)符合那幾個(gè)可積分和收斂的定義就可以了，因此傅立葉變換的"波"因子，就可以不使用三角函數(shù)，而是使用一系列從某些基本函數(shù)構(gòu)造出來的函數(shù)族，只要這個(gè)基本函數(shù)符合那些收斂和正交的條件就可以了。怎么構(gòu)造這樣的基本函數(shù)呢?sin(t)被加了方形窗以后，映射到頻域是一堆無窮的散列脈沖，所以不能再用三角函數(shù)了。我們要得到頻率域收斂性好的函數(shù)族，能覆蓋頻率域的低端部分。說的遠(yuǎn)一點(diǎn)，如果是取數(shù)字信號(hào)的小波變換，那么基礎(chǔ)小波要保證數(shù)字角頻率是最大的2Pi。利用小波進(jìn)行離頻譜分析的方法，不是像傅立葉級(jí)數(shù)那樣求出所有的頻率分量，也不是向傅立葉變換那樣看頻譜特性，而是做某種濾波，看看在某種數(shù)字角頻率的波峰值大概是多少。可以根據(jù)實(shí)際需要得到如干個(gè)數(shù)字序列。

我們采用(0,f),(f,2f),(2f,4f)這樣的倍頻關(guān)系來考察函數(shù)族的頻率特性，那么對(duì)應(yīng)的時(shí)間波形就是倍數(shù)擴(kuò)展(且包含調(diào)制---所以才有頻譜搬移)的一系列函數(shù)族。頻域是窗函數(shù)的基本函數(shù)，時(shí)域就是鐘形函數(shù)。當(dāng)然其他類型的小波，雖然頻率域不是窗函數(shù)，但是仍然可用：因?yàn)樾〔ǚe分求出來的變換，是一個(gè)值，例如(0,f)里包含的總能量值，(f,2f)里面包含的總能量值。所以即使頻域的分割不是用長方形而是其他的圖形，對(duì)于結(jié)果來說影響不大。同時(shí)，這個(gè)頻率域的值，它的分辨率密度和時(shí)域小波基函數(shù)的時(shí)間分辨率是沖突的(時(shí)域緊頻域?qū)挘瑫r(shí)域?qū)掝l域緊)，所以設(shè)計(jì)的時(shí)候受到海森堡測(cè)不準(zhǔn)原理的制約。Jpeg2000壓縮就是小波：因?yàn)闀r(shí)頻都是局部的，變換結(jié)果是數(shù)值點(diǎn)而不是向量，所以，計(jì)算復(fù)雜度從FFT的O(NlgN)下降到了O(N)，性能非常好。

審核編輯：湯梓紅