我以前的文章主要都是講解算法的原理和解題的思維,對時間復雜度和空間復雜度的分析經常一筆帶過,主要是基于以下兩個原因:
1、對于偏小白的讀者,希望你集中精力理解算法原理。如果加入太多偏數(shù)學的內容,很容易把人勸退。
2、正確理解常用算法底層原理,是進行復雜度的分析的前提。尤其是遞歸相關的算法,只有你從樹的角度進行思考和分析,才能正確分析其復雜度。
鑒于現(xiàn)在歷史文章已經涵蓋了所有常見算法的核心原理,所以我專門寫一篇時空復雜度的分析指南,授人以魚不如授人以漁,教給你一套通用的方法分析任何算法的時空復雜度。
本文會篇幅較長,會涵蓋如下幾點:
1、Big O 表示法的幾個基本特點。
2、非遞歸算法中的時間復雜度分析。
3、數(shù)據結構 API 的效率衡量方法(攤還分析)。
4、遞歸算法的時間/空間復雜度的分析方法,這部分是重點,我會用動態(tài)規(guī)劃和回溯算法舉例。
廢話不多說了,接下來一個個看。
Big O 表示法
首先看一下 Big O 記號的數(shù)學定義:
O(g(n))= {f(n): 存在正常量c和n_0,使得對所有n ≥ n_0,有0 ≤ f(n) ≤ c*g(n)}
我們常用的這個符號O其實代表一個函數(shù)的集合,比如O(n^2)代表著一個由g(n) = n^2派生出來的一個函數(shù)集合;我們說一個算法的時間復雜度為O(n^2),意思就是描述該算法的復雜度的函數(shù)屬于這個函數(shù)集合之中。
理論上,你看明白這個抽象的數(shù)學定義,就可以解答你關于 Big O 表示法的一切疑問了 。
但考慮到大部分人看到數(shù)學定義就頭暈,我給你列舉兩個復雜度分析中會用到的特性,記住這兩個就夠用了。
1、只保留增長速率最快的項,其他的項可以省略 。
首先,乘法和加法中的常數(shù)因子都可以忽略不計,比如下面的例子:
O(2N + 100) = O(N)
O(2^(N+1)) = O(2 * 2^N) = O(2^N)
O(M + 3N + 99) = O(M + N)
當然,不要見到常數(shù)就消,有的常數(shù)消不得:
O(2^(2N)) = O(4^N)
除了常數(shù)因子,增長速率慢的項在增長速率快的項面前也可以忽略不計:
O(N^3 + 999 * N^2 + 999 * N) = O(N^3)
O((N + 1) * 2^N) = O(N * 2^N + 2^N) = O(N * 2^N)
以上列舉的都是最簡單常見的例子,這些例子都可以被 Big O 記號的定義正確解釋。如果你遇到更復雜的復雜度場景,也可以根據定義來判斷自己的復雜度表達式是否正確。
2、Big O 記號表示復雜度的「上界」 。
換句話說,只要你給出的是一個上界,用 Big O 記號表示就都是正確的。
比如如下代碼:
for (int i = 0; i < N; i++) {
print("hello world");
}
如果說這是一個算法,那么顯然它的時間復雜度是O(N)。但如果你非要說它的時間復雜度是O(N^2),嚴格意義上講是可以的,因為O記號表示一個上界嘛,這個算法的時間復雜度確實不會超過N^2這個上界呀,雖然這個上界不夠「緊」,但符合定義,所以沒毛病。
上述例子太簡單,非要擴大它的時間復雜度上界顯得沒什么意義。但有些算法的復雜度會和算法的輸入數(shù)據有關,沒辦法提前給出一個特別精確的時間復雜度,那么在這種情況下,用 Big O 記號擴大時間復雜度的上界就變得有意義了。
比如前文 動態(tài)規(guī)劃核心框架中講到的湊零錢問題的暴力遞歸解法,核心代碼框架如下:
// 定義:要湊出金額 n,至少要 dp(coins, n) 個硬幣
int dp(int[] coins, int amount) {
// base case
if (amount <= 0) return;
// 狀態(tài)轉移
for (int coin : coins) {
dp(coins, amount - coin);
}
}
當amount = 11, coins = [1,2,5]時,算法的遞歸樹就長這樣:
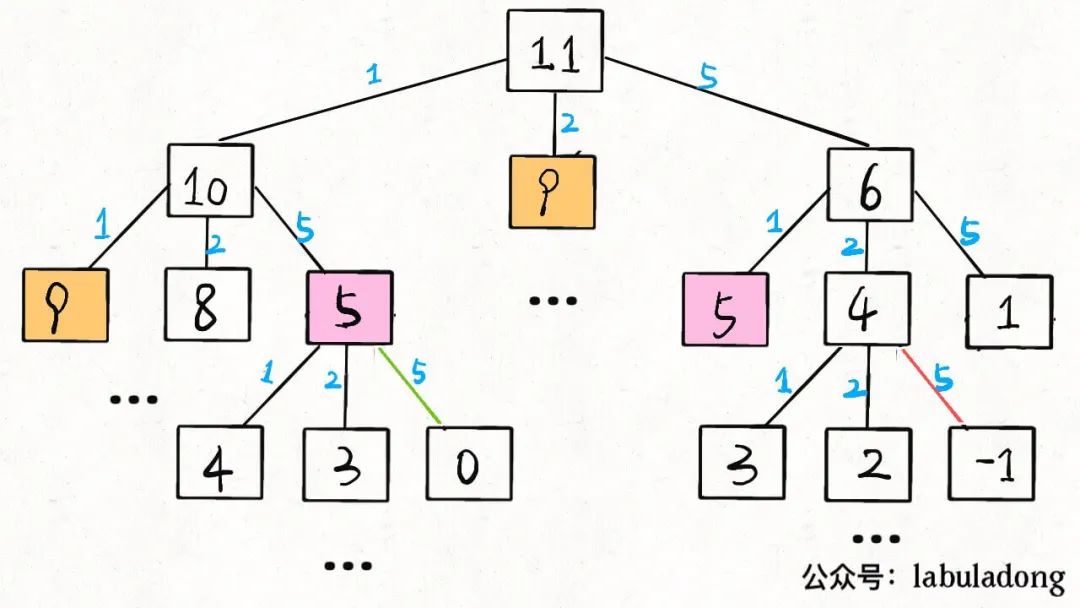
后文會具體講遞歸算法的時間復雜度計算方法,現(xiàn)在我們先求一下這棵遞歸樹上的節(jié)點個數(shù)吧。
假設金額amount的值為N,coins列表中元素個數(shù)為K,那么這棵遞歸樹就是一棵K叉樹。但這棵樹的生長和coins列表中的硬幣面額有直接的關系,所以這棵樹的形狀會很不規(guī)則,導致我們很難精確地求出樹上節(jié)點的總數(shù)。
對于這種情況,比較簡單的處理方式就是按最壞情況做近似處理:
這棵樹的高度有多高?不知道,那就按最壞情況來處理,假設全都是面額為 1 的硬幣,這種情況下樹高為N。
這棵樹的結構是什么樣的?不知道,那就按最壞情況來處理,假設它是一棵滿K叉樹好了。
那么,這棵樹上共有多少節(jié)點?都按最壞情況來處理,高度為N的一棵滿K叉樹,其節(jié)點總數(shù)為K^N - 1,用 Big O 表示就是O(K^N)。
當然,我們知道這棵樹上的節(jié)點數(shù)其實沒有這么多,但用O(K^N)表示一個上界是沒問題的。
所以,有時候你自己估算出來的時間復雜度和別人估算的復雜度不同,并不一定代表誰算錯了,可能你倆都是對的,只是是估算的精度不同 ,一般來說只要數(shù)量級(線性/指數(shù)級/對數(shù)級/平方級等)能對上就沒問題。
在算法領域,除了用 Big O 表示漸進上界,還有漸進下界、漸進緊確界等邊界的表示方法,有興趣的讀者可以自行搜索。不過從實用的角度看,以上對 Big O 記號表示法的講解就夠用了。
非遞歸算法分析
非遞歸算法的空間復雜度一般很容易計算,你看它有沒有申請數(shù)組之類的存儲空間就行了,所以我主要說下時間復雜度的分析。
非遞歸算法中嵌套循環(huán)很常見,大部分場景下,只需把每一層的復雜度相乘就是總的時間復雜度:
// 復雜度 O(N*W)
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
dp[i][w] = ...;
}
}
// 1 + 2 + ... + n = n/2 + (n^2)/2
// 用 Big O 表示化簡為 O(n^2)
for (int i = 0; i < n; i++) {
for (int j = i; j >= 0; j--) {
dp[i][j] = ...;
}
}
但有時候只看嵌套循環(huán)的層數(shù)并不準確,還得看算法 具體在做什么 ,比如前文一文秒殺所有 nSum 問題) 中就有這樣一段代碼:
// 左右雙指針
int lo = 0, hi = nums.length;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
這段代碼看起來很復雜,大 while 循環(huán)里面套了好多小 while 循環(huán),感覺這段代碼的時間復雜度應該是O(N^2)(N代表nums的長度)?
其實,你只需要搞清楚代碼到底在干什么,就能輕松計算出正確的復雜度了 。
這段代碼就是個左右雙指針嘛,lo是左邊的指針,hi是右邊的指針,這兩個指針相向而行,相遇時外層 while 結束。
甭管多復雜的邏輯,你看lo指針一直在往右走(lo++),hi指針一直在往左走(hi--),它倆有沒有回退過?沒有。
所以這段算法的邏輯就是lo和hi不斷相向而行,相遇時算法結束,那么它的時間復雜度就是線性的O(N)。
類似的,你看前文 滑動窗口算法核心框架給出的滑動窗口算法模板:
/* 滑動窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
// 雙指針,維護 [left, right) 為窗口
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
right++;
// 判斷左側窗口是否要收縮
while (window needs shrink) {
// 縮小窗口
left++;
}
}
}
乍一看也是個嵌套循環(huán),但仔細觀察,發(fā)現(xiàn)這也是個雙指針技巧,left和right指針從 0 開始,一直向右移,直到移動到s的末尾結束外層 while 循環(huán),沒有回退過。
那么該算法做的事情就是把left和right兩個指針從 0 移動到N(N代表字符串s的長度),所以滑動窗口算法的時間復雜度為線性的O(N)。
數(shù)據結構分析
因為數(shù)據結構會用來存儲數(shù)據,其 API 的執(zhí)行效率可能受到其中存儲的數(shù)據的影響,所以衡量數(shù)據結構 API 效率的方法和衡量普通算法函數(shù)效率的方法是有一些區(qū)別的。
就拿我們常見的數(shù)據結構舉例,比如很多語言都提供動態(tài)數(shù)組,可以自動進行擴容和縮容。在它的尾部添加元素的時間復雜度是O(1)。但當?shù)讓訑?shù)組擴容時會分配新內存并把原來的數(shù)據搬移到新數(shù)組中,這個時間復雜度就是O(N)了,那我們能說在數(shù)組尾部添加元素的時間復雜度就是O(N)嗎?
再比如哈希表也會在負載因子達到某個閾值時進行擴容和 rehash,時間復雜度也會達到O(N),那么我們?yōu)槭裁催€說哈希表對單個鍵值對的存取效率是O(1)呢?
答案就是, 如果想衡量數(shù)據結構類中的某個方法的時間復雜度,不能簡單地看最壞時間復雜度,而應該看攤還(平均)時間復雜度 。
比如說前文 [特殊數(shù)據結構:單調隊列實現(xiàn)的單調隊列類:
/* 單調隊列的實現(xiàn) */
class MonotonicQueue {
LinkedList
標準的隊列實現(xiàn)中,push和pop方法的時間復雜度應該都是O(1),但這個MonotonicQueue類的push方法包含一個循環(huán),其復雜度取決于參數(shù)e,最好情況下是O(1),而最壞情況下復雜度應該是O(N),N為隊列中的元素個數(shù)。
對于這種情況,我們用平均時間復雜度來衡量push方法的效率比較合理。雖然它包含循環(huán),但它的平均時間復雜度依然為O(1)。
-
算法
+關注
關注
23文章
4600瀏覽量
92646 -
API
+關注
關注
2文章
1485瀏覽量
61817 -
函數(shù)
+關注
關注
3文章
4307瀏覽量
62432 -
數(shù)據結構
+關注
關注
3文章
573瀏覽量
40093
發(fā)布評論請先 登錄
相關推薦
基于紋理復雜度的快速幀內預測算法
時間復雜度是指什么
各種排序算法的時間空間復雜度、穩(wěn)定性
一種低復雜度的MIMO-OFDM信道估計閾值算法
LDPC碼低復雜度譯碼算法研究

圖像復雜度對信息隱藏性能影響分析
如何求遞歸算法的時間復雜度
常見機器學習算法的計算復雜度
算法時空復雜度分析實用指南2
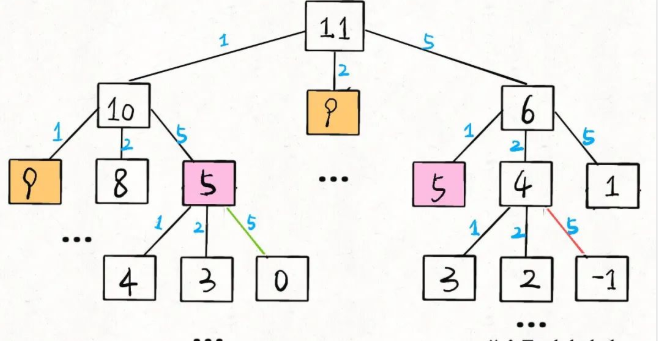




 算法時空復雜度分析實用指南1
算法時空復雜度分析實用指南1










評論