島嶼問(wèn)題是經(jīng)典的面試高頻題，雖然基本的島嶼問(wèn)題并不難，但是島嶼問(wèn)題有一些有意思的擴(kuò)展，比如求子島嶼數(shù)量，求形狀不同的島嶼數(shù)量等等，本文就來(lái)把這些問(wèn)題一網(wǎng)打盡。

島嶼系列問(wèn)題的核心考點(diǎn)就是用 DFS/BFS 算法遍歷二維數(shù)組 。

本文主要來(lái)講解如何用 DFS 算法來(lái)秒殺島嶼系列問(wèn)題，不過(guò)用 BFS 算法的核心思路是完全一樣的，無(wú)非就是把 DFS 改寫(xiě)成 BFS 而已。

那么如何在二維矩陣中使用 DFS 搜索呢？如果你把二維矩陣中的每一個(gè)位置看做一個(gè)節(jié)點(diǎn)，這個(gè)節(jié)點(diǎn)的上下左右四個(gè)位置就是相鄰節(jié)點(diǎn)，那么整個(gè)矩陣就可以抽象成一幅網(wǎng)狀的「圖」結(jié)構(gòu)。

根據(jù) [學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)和算法的框架思維]，完全可以根據(jù)二叉樹(shù)的遍歷框架改寫(xiě)出二維矩陣的 DFS 代碼框架：

// 二叉樹(shù)遍歷框架
void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
}

// 二維矩陣遍歷框架
void dfs(int[][] grid, int i, int j, boolean[] visited) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引邊界
        return;
    }
    if (visited[i][j]) {
        // 已遍歷過(guò) (i, j)
        return;
    }
    // 前序：進(jìn)入節(jié)點(diǎn) (i, j)
    visited[i][j] = true;
    dfs(grid, i - 1, j); // 上
    dfs(grid, i + 1, j); // 下
    dfs(grid, i, j - 1); // 左
    dfs(grid, i, j + 1); // 右
    // 后序：離開(kāi)節(jié)點(diǎn) (i, j)
    // visited[i][j] = true;
}

因?yàn)槎S矩陣本質(zhì)上是一幅「圖」，所以遍歷的過(guò)程中需要一個(gè)visited布爾數(shù)組防止走回頭路，如果你能理解上面這段代碼，那么搞定所有島嶼問(wèn)題都很簡(jiǎn)單。

這里額外說(shuō)一個(gè)處理二維數(shù)組的常用小技巧，你有時(shí)會(huì)看到使用「方向數(shù)組」來(lái)處理上下左右的遍歷，和前文 [圖遍歷框架]的代碼很類(lèi)似：

// 方向數(shù)組，分別代表上、下、左、右
int[][] dirs = new int[][]{{-1,0}, {1,0}, {0,-1}, {0,1}};

void dfs(int[][] grid, int i, int j, boolean[] visited) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引邊界
        return;
    }
    if (visited[i][j]) {
        // 已遍歷過(guò) (i, j)
        return;
    }

    // 進(jìn)入節(jié)點(diǎn) (i, j)
    visited[i][j] = true;
    // 遞歸遍歷上下左右的節(jié)點(diǎn)
    for (int[] d : dirs) {
        int next_i = i + d[0];
        int next_j = j + d[1];
        dfs(grid, next_i, next_j);
    }
    // 離開(kāi)節(jié)點(diǎn) (i, j)
    // visited[i][j] = true;
}

這種寫(xiě)法無(wú)非就是用 for 循環(huán)處理上下左右的遍歷罷了，你可以按照個(gè)人喜好選擇寫(xiě)法。

島嶼數(shù)量

這是力扣第 200 題「島嶼數(shù)量」，最簡(jiǎn)單也是最經(jīng)典的一道島嶼問(wèn)題，題目會(huì)輸入一個(gè)二維數(shù)組grid，其中只包含0或者1，0代表海水，1代表陸地，且假設(shè)該矩陣四周都是被海水包圍著的。

我們說(shuō)連成片的陸地形成島嶼，那么請(qǐng)你寫(xiě)一個(gè)算法，計(jì)算這個(gè)矩陣grid中島嶼的個(gè)數(shù)，函數(shù)簽名如下：

int numIslands(char[][] grid);

比如說(shuō)題目給你輸入下面這個(gè)grid有四片島嶼，算法應(yīng)該返回 4：

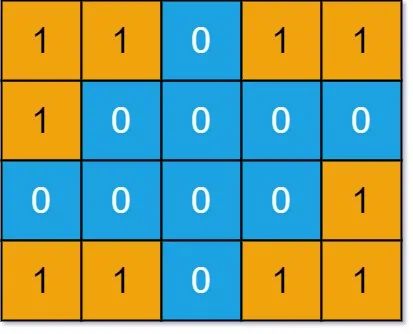
思路很簡(jiǎn)單，關(guān)鍵在于如何尋找并標(biāo)記「島嶼」，這就要 DFS 算法發(fā)揮作用了，我們直接看解法代碼：

// 主函數(shù)，計(jì)算島嶼數(shù)量
int numIslands(char[][] grid) {
    int res = 0;
    int m = grid.length, n = grid[0].length;
    // 遍歷 grid
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == '1') {
                // 每發(fā)現(xiàn)一個(gè)島嶼，島嶼數(shù)量加一
                res++;
                // 然后使用 DFS 將島嶼淹了
                dfs(grid, i, j);
            }
        }
    }
    return res;
}

// 從 (i, j) 開(kāi)始，將與之相鄰的陸地都變成海水
void dfs(char[][] grid, int i, int j) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引邊界
        return;
    }
    if (grid[i][j] == '0') {
        // 已經(jīng)是海水了
        return;
    }
    // 將 (i, j) 變成海水
    grid[i][j] = '0';
    // 淹沒(méi)上下左右的陸地
    dfs(grid, i + 1, j);
    dfs(grid, i, j + 1);
    dfs(grid, i - 1, j);
    dfs(grid, i, j - 1);
}

為什么每次遇到島嶼，都要用 DFS 算法把島嶼「淹了」呢？主要是為了省事，避免維護(hù)visited數(shù)組 。

因?yàn)?code>dfs函數(shù)遍歷到值為0的位置會(huì)直接返回，所以只要把經(jīng)過(guò)的位置都設(shè)置為0，就可以起到不走回頭路的作用。

PS：這類(lèi) DFS 算法還有個(gè)別名叫做 [FloodFill 算法]，現(xiàn)在有沒(méi)有覺(jué)得 FloodFill 這個(gè)名字還挺貼切的~

這個(gè)最最基本的島嶼問(wèn)題就說(shuō)到這，我們來(lái)看看后面的題目有什么花樣。

封閉島嶼的數(shù)量

上一題說(shuō)二維矩陣四周可以認(rèn)為也是被海水包圍的，所以靠邊的陸地也算作島嶼。

力扣第 1254 題「統(tǒng)計(jì)封閉島嶼的數(shù)目」和上一題有兩點(diǎn)不同：

1、用0表示陸地，用1表示海水。

2、讓你計(jì)算「封閉島嶼」的數(shù)目。所謂「封閉島嶼」就是上下左右全部被1包圍的0，也就是說(shuō) 靠邊的陸地不算作「封閉島嶼」 。

函數(shù)簽名如下：

int closedIsland(int[][] grid)

比如題目給你輸入如下這個(gè)二維矩陣：

算法返回 2，只有圖中灰色部分的0是四周全都被海水包圍著的「封閉島嶼」。

那么如何判斷「封閉島嶼」呢？其實(shí)很簡(jiǎn)單，把上一題中那些靠邊的島嶼排除掉，剩下的不就是「封閉島嶼」了嗎 ？

有了這個(gè)思路，就可以直接看代碼了，注意這題規(guī)定0表示陸地，用1表示海水：

// 主函數(shù)：計(jì)算封閉島嶼的數(shù)量
int closedIsland(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    for (int j = 0; j < n; j++) {
        // 把靠上邊的島嶼淹掉
        dfs(grid, 0, j);
        // 把靠下邊的島嶼淹掉
        dfs(grid, m - 1, j);
    }
    for (int i = 0; i < m; i++) {
        // 把靠左邊的島嶼淹掉
        dfs(grid, i, 0);
        // 把靠右邊的島嶼淹掉
        dfs(grid, i, n - 1);
    }
    // 遍歷 grid，剩下的島嶼都是封閉島嶼
    int res = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 0) {
                res++;
                dfs(grid, i, j);
            }
        }
    }
    return res;
}

// 從 (i, j) 開(kāi)始，將與之相鄰的陸地都變成海水
void dfs(int[][] grid, int i, int j) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        return;
    }
    if (grid[i][j] == 1) {
        // 已經(jīng)是海水了
        return;
    }
    // 將 (i, j) 變成海水
    grid[i][j] = 1;
    // 淹沒(méi)上下左右的陸地
    dfs(grid, i + 1, j);
    dfs(grid, i, j + 1);
    dfs(grid, i - 1, j);
    dfs(grid, i, j - 1);
}

只要提前把靠邊的陸地都淹掉，然后算出來(lái)的就是封閉島嶼了。

PS：處理這類(lèi)島嶼問(wèn)題除了 DFS/BFS 算法之外，Union Find 并查集算法也是一種可選的方法，前文 [Union Find 算法運(yùn)用] 就用 Union Find 算法解決了一道類(lèi)似的問(wèn)題。

這道島嶼題目的解法稍微改改就可以解決力扣第 1020 題「飛地的數(shù)量」，這題不讓你求封閉島嶼的數(shù)量，而是求封閉島嶼的面積總和。

其實(shí)思路都是一樣的，先把靠邊的陸地淹掉，然后去數(shù)剩下的陸地?cái)?shù)量就行了，注意第 1020 題中1代表陸地，0代表海水：

int numEnclaves(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    // 淹掉靠邊的陸地
    for (int i = 0; i < m; i++) {
        dfs(grid, i, 0);
        dfs(grid, i, n - 1);
    }
    for (int j = 0; j < n; j++) {
        dfs(grid, 0, j);
        dfs(grid, m - 1, j);
    }

    // 數(shù)一數(shù)剩下的陸地
    int res = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 1) {
                res += 1;
            }
        }
    }

    return res;
}

// 和之前的實(shí)現(xiàn)類(lèi)似
void dfs(int[][] grid, int i, int j) {
    // ...
}

篇幅所限，具體代碼我就不寫(xiě)了，我們繼續(xù)看其他的島嶼問(wèn)題。

島嶼的最大面積

這是力扣第 695 題「島嶼的最大面積」，0表示海水，1表示陸地，現(xiàn)在不讓你計(jì)算島嶼的個(gè)數(shù)了，而是讓你計(jì)算最大的那個(gè)島嶼的面積，函數(shù)簽名如下：

int maxAreaOfIsland(int[][] grid)

比如題目給你輸入如下一個(gè)二維矩陣：

其中面積最大的是橘紅色的島嶼，算法返回它的面積 6。

這題的大體思路和之前完全一樣，只不過(guò)dfs函數(shù)淹沒(méi)島嶼的同時(shí)，還應(yīng)該想辦法記錄這個(gè)島嶼的面積 。

我們可以給dfs函數(shù)設(shè)置返回值，記錄每次淹沒(méi)的陸地的個(gè)數(shù)，直接看解法吧：

int maxAreaOfIsland(int[][] grid) {
    // 記錄島嶼的最大面積
    int res = 0;
    int m = grid.length, n = grid[0].length;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 1) {
                // 淹沒(méi)島嶼，并更新最大島嶼面積
                res = Math.max(res, dfs(grid, i, j));
            }
        }
    }
    return res;
}

// 淹沒(méi)與 (i, j) 相鄰的陸地，并返回淹沒(méi)的陸地面積
int dfs(int[][] grid, int i, int j) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引邊界
        return 0;
    }
    if (grid[i][j] == 0) {
        // 已經(jīng)是海水了
        return 0;
    }
    // 將 (i, j) 變成海水
    grid[i][j] = 0;

    return dfs(grid, i + 1, j)
         + dfs(grid, i, j + 1)
         + dfs(grid, i - 1, j)
         + dfs(grid, i, j - 1) + 1;
}

解法和之前相比差不多，我也不多說(shuō)了，接下來(lái)的兩道島嶼問(wèn)題是比較有技巧性的，我們重點(diǎn)來(lái)看一下。

子島嶼數(shù)量

如果說(shuō)前面的題目都是模板題，那么力扣第 1905 題「統(tǒng)計(jì)子島嶼」可能得動(dòng)動(dòng)腦子了：

這道題的關(guān)鍵在于，如何快速判斷子島嶼 ？肯定可以借助 [Union Find 并查集算法] 來(lái)判斷，不過(guò)本文重點(diǎn)在 DFS 算法，就不展開(kāi)并查集算法了。

什么情況下grid2中的一個(gè)島嶼B是grid1中的一個(gè)島嶼A的子島？

當(dāng)島嶼B中所有陸地在島嶼A中也是陸地的時(shí)候，島嶼B是島嶼A的子島。

反過(guò)來(lái)說(shuō)，如果島嶼B中存在一片陸地，在島嶼A的對(duì)應(yīng)位置是海水，那么島嶼B就不是島嶼A的子島 。

那么，我們只要遍歷grid2中的所有島嶼，把那些不可能是子島的島嶼排除掉，剩下的就是子島。

依據(jù)這個(gè)思路，可以直接寫(xiě)出下面的代碼：

int countSubIslands(int[][] grid1, int[][] grid2) {
    int m = grid1.length, n = grid1[0].length;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid1[i][j] == 0 && grid2[i][j] == 1) {
                // 這個(gè)島嶼肯定不是子島，淹掉
                dfs(grid2, i, j);
            }
        }
    }
    // 現(xiàn)在 grid2 中剩下的島嶼都是子島，計(jì)算島嶼數(shù)量
    int res = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid2[i][j] == 1) {
                res++;
                dfs(grid2, i, j);
            }
        }
    }
    return res;
}

// 從 (i, j) 開(kāi)始，將與之相鄰的陸地都變成海水
void dfs(int[][] grid, int i, int j) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        return;
    }
    if (grid[i][j] == 0) {
        return;
    }

    grid[i][j] = 0;
    dfs(grid, i + 1, j);
    dfs(grid, i, j + 1);
    dfs(grid, i - 1, j);
    dfs(grid, i, j - 1);
}

這道題的思路和計(jì)算「封閉島嶼」數(shù)量的思路有些類(lèi)似，只不過(guò)后者排除那些靠邊的島嶼，前者排除那些不可能是子島的島嶼。

不同的島嶼數(shù)量

這是本文的最后一道島嶼題目，作為壓軸題，當(dāng)然是最有意思的。

力扣第 694 題「不同的島嶼數(shù)量」，題目還是輸入一個(gè)二維矩陣，0表示海水，1表示陸地，這次讓你計(jì)算 不同的 (distinct) 島嶼數(shù)量，函數(shù)簽名如下：

int numDistinctIslands(int[][] grid)

比如題目輸入下面這個(gè)二維矩陣：

其中有四個(gè)島嶼，但是左下角和右上角的島嶼形狀相同，所以不同的島嶼共有三個(gè)，算法返回 3。

很顯然我們得想辦法把二維矩陣中的「島嶼」進(jìn)行轉(zhuǎn)化，變成比如字符串這樣的類(lèi)型，然后利用 HashSet 這樣的數(shù)據(jù)結(jié)構(gòu)去重，最終得到不同的島嶼的個(gè)數(shù)。

如果想把島嶼轉(zhuǎn)化成字符串，說(shuō)白了就是序列化，序列化說(shuō)白了遍歷嘛，前文 [二叉樹(shù)的序列化和反序列化]講了二叉樹(shù)和字符串互轉(zhuǎn)，這里也是類(lèi)似的。

首先，對(duì)于形狀相同的島嶼，如果從同一起點(diǎn)出發(fā)，dfs函數(shù)遍歷的順序肯定是一樣的 。

因?yàn)楸闅v順序是寫(xiě)死在你的遞歸函數(shù)里面的，不會(huì)動(dòng)態(tài)改變：

void dfs(int[][] grid, int i, int j) {
    // 遞歸順序：
    dfs(grid, i - 1, j); // 上
    dfs(grid, i + 1, j); // 下
    dfs(grid, i, j - 1); // 左
    dfs(grid, i, j + 1); // 右
}

所以，遍歷順序從某種意義上說(shuō)就可以用來(lái)描述島嶼的形狀，比如下圖這兩個(gè)島嶼：

假設(shè)它們的遍歷順序是：

下，右，上，撤銷(xiāo)上，撤銷(xiāo)右，撤銷(xiāo)下

如果我用分別用1, 2, 3, 4代表上下左右，用-1, -2, -3, -4代表上下左右的撤銷(xiāo)，那么可以這樣表示它們的遍歷順序：

2, 4, 1, -1, -4, -2

你看，這就相當(dāng)于是島嶼序列化的結(jié)果，只要每次使用dfs遍歷島嶼的時(shí)候生成這串?dāng)?shù)字進(jìn)行比較，就可以計(jì)算到底有多少個(gè)不同的島嶼了 。

要想生成這段數(shù)字，需要稍微改造dfs函數(shù)，添加一些函數(shù)參數(shù)以便記錄遍歷順序：

void dfs(int[][] grid, int i, int j, StringBuilder sb, int dir) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n 
        || grid[i][j] == 0) {
        return;
    }
    // 前序遍歷位置：進(jìn)入 (i, j)
    grid[i][j] = 0;
    sb.append(dir).append(',');

    dfs(grid, i - 1, j, sb, 1); // 上
    dfs(grid, i + 1, j, sb, 2); // 下
    dfs(grid, i, j - 1, sb, 3); // 左
    dfs(grid, i, j + 1, sb, 4); // 右

    // 后序遍歷位置：離開(kāi) (i, j)
    sb.append(-dir).append(',');
}

dir記錄方向，dfs函數(shù)遞歸結(jié)束后，sb記錄著整個(gè)遍歷順序，其實(shí)這就是前文 [回溯算法核心套路]說(shuō)到的回溯算法框架，你看到頭來(lái)這些算法都是相通的。

有了這個(gè)dfs函數(shù)就好辦了，我們可以直接寫(xiě)出最后的解法代碼：

int numDistinctIslands(int[][] grid) {
    int m = grid.length, n = grid[0].length;
    // 記錄所有島嶼的序列化結(jié)果
    HashSet

這樣，這道題就解決了，至于為什么初始調(diào)用dfs函數(shù)時(shí)的dir參數(shù)可以隨意寫(xiě)，這里涉及 DFS 和回溯算法的一個(gè)細(xì)微差別，前文 [圖算法基礎(chǔ)]有寫(xiě)，這里就不展開(kāi)了。

以上就是全部島嶼系列問(wèn)題的解題思路，也許前面的題目大部分人會(huì)做，但是最后兩題還是比較巧妙的，希望本文對(duì)你有幫助。