SVPWM(Space Vector Pulse Width Modulation),即空間矢量脈寬調制。SVPWM的理論基礎是平均值等效原理,即在一個開關周期Ts內,對基本矢量電壓加以組合,使其平均值與給定電壓矢量相等。通過控制基本矢量電壓的作用時間,使合成的目標矢量電壓在空間位置按照接近圓形軌跡旋轉,所產生的實際磁通去逼近一個理想的磁通圓。模型如下圖所示,采樣點數越多,就越逼近理想磁通圓,理論上采樣點數無窮多時就是理想磁通圓了。
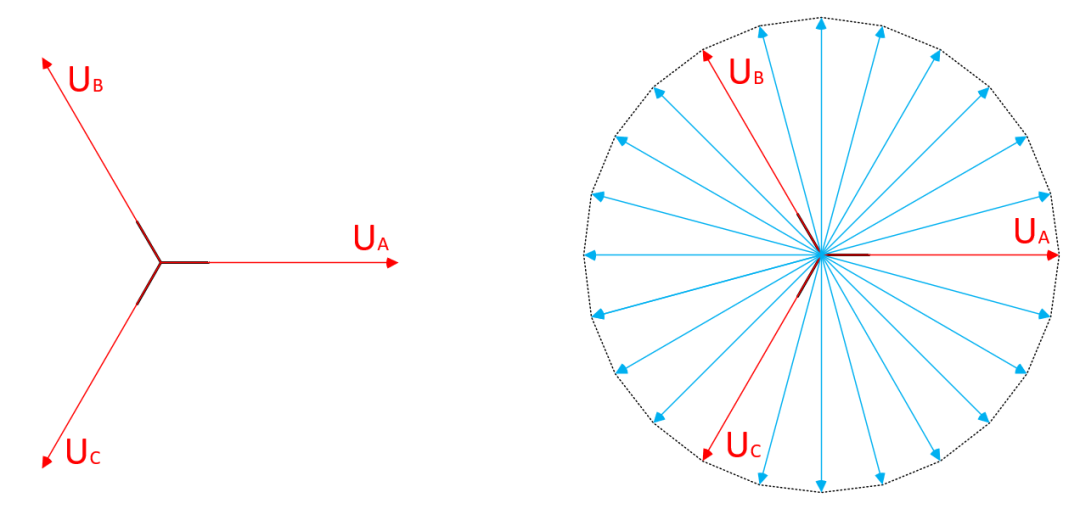
左圖:基本電壓矢量圖; 右圖:實際磁通圓軌跡示意圖
加在三相繞組線圈上的端電壓都為正弦電壓,設峰值為Um,兩兩相位差120°,記為:
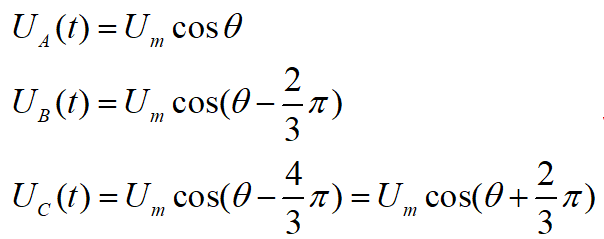
注意:這里的電壓是標量,只是電壓幅值按正弦變化。
在二維平面上,三相繞組ABC構成的坐標系,兩兩坐標軸相差120°,則三相基本電壓用矢量表示為:
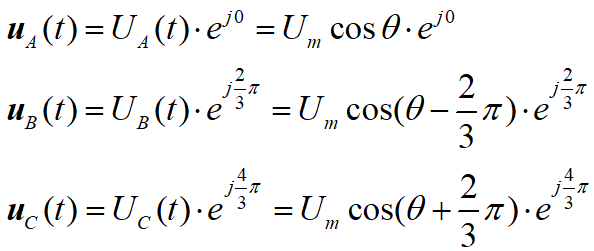
用歐拉公式
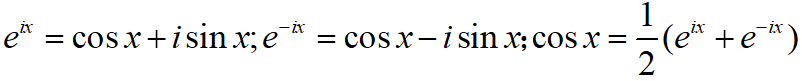
展開上式,并計算其矢量和
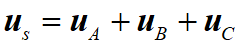
下面是展開計算的過程:
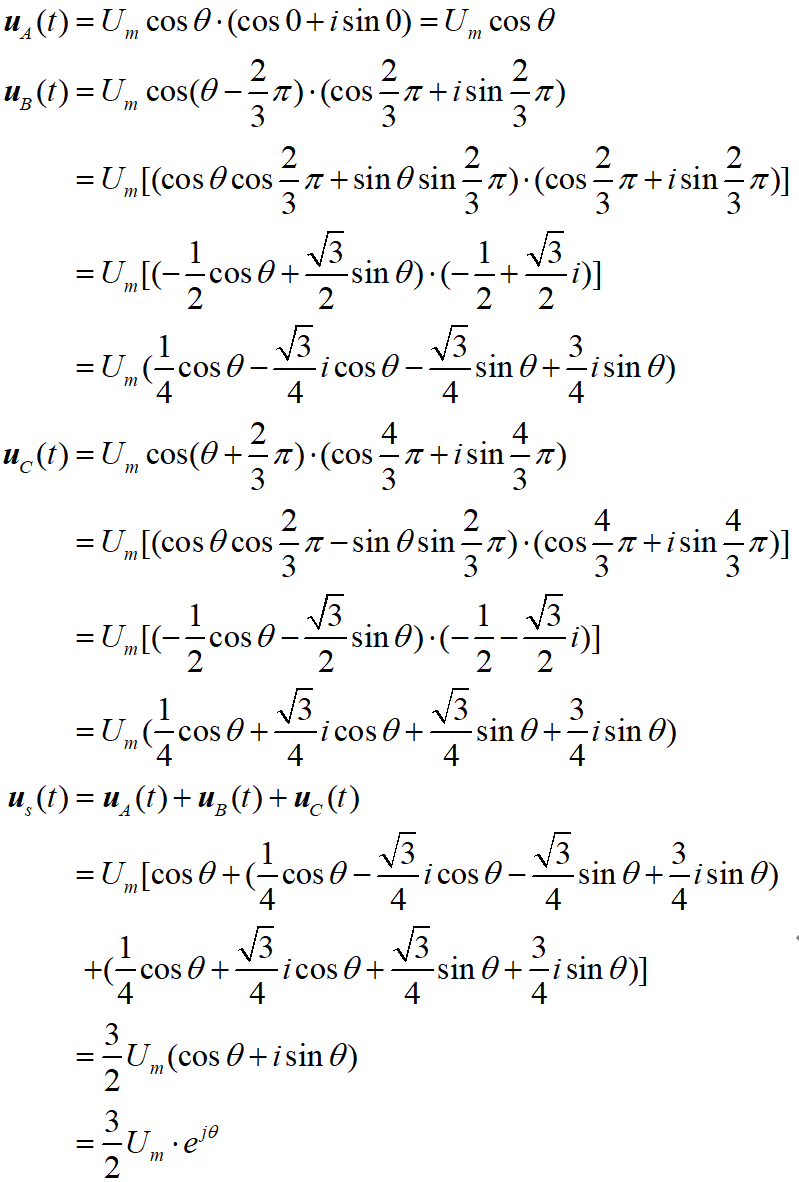
在計算過程中用到了三角函數的展開公式:
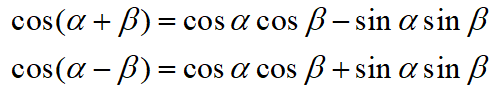
原理總結:
通過在 空間位置上兩兩相差120° 的三個基本電壓來合成目標電壓。三個基本電壓的方向不變,幅值按正弦規律變化, 相位兩兩相差120° ;合成的目標矢量電壓其幅值固定不變,為相電壓峰值的1.5倍,方向在空間旋轉,旋轉的角速度等于相電壓幅值變化的角速度。
02. SVPWM實現方法
2.1 基本矢量電壓:
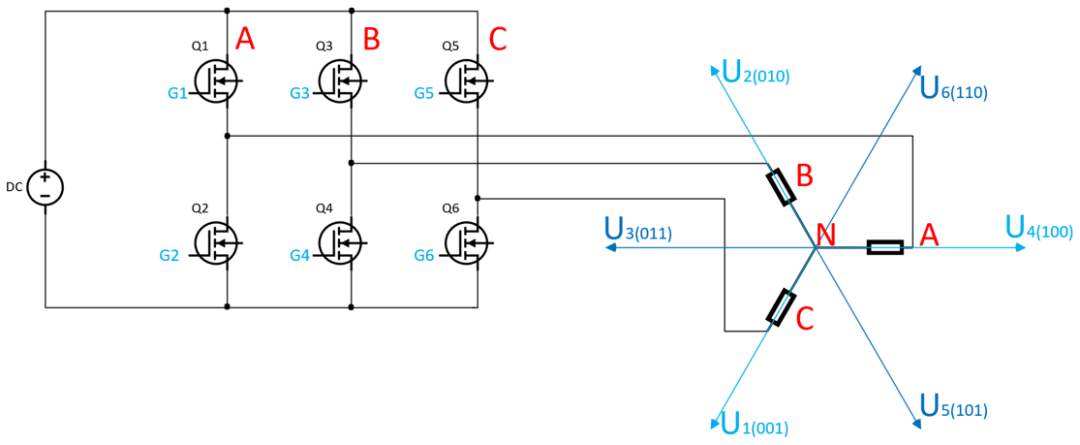
如下圖所示,逆變器的三相橋臂共有6個開關管(Q1,Q2,Q3,Q4,Q5,Q6),對于每一個半橋,同一時刻只能有一個開關管導通,即控制信號G1和G2反相,G3和G4反相,G5和G6反相,如果同一個半橋的上下橋臂同時導通則會導致電源Udc短路。逆變器三個半橋的輸出分別加到電機的ABC三相繞上,三相繞組在空間位置上兩兩相差120°。
定義開關函數

如S(A)=1表示Q1導通Q2截止,母線電壓Udc加到A相繞組;
再比如S(B)=1表示Q3截止Q4導通,B相繞組連接到電源負極,即GND。
ABC三個開關函數的狀態(S(A),S(B),S(C))共有8種組合,分別是{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1),},分別對應8個矢量電壓,其中2個零矢量電壓是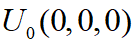 和
和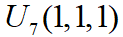 ,6個非零矢量電壓分別是
,6個非零矢量電壓分別是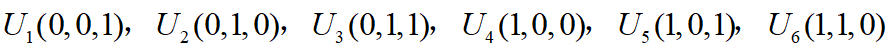 ,它們在空間位置上相鄰間隔60°,將平面等分為6個扇區。
,它們在空間位置上相鄰間隔60°,將平面等分為6個扇區。
以三相繞組的公共端N點作為參考零電位,各基本矢量電壓的方向如上圖所示,在三相坐標系下,這6個非零基本矢量電壓的幅值為Udc,具體如下表所示。
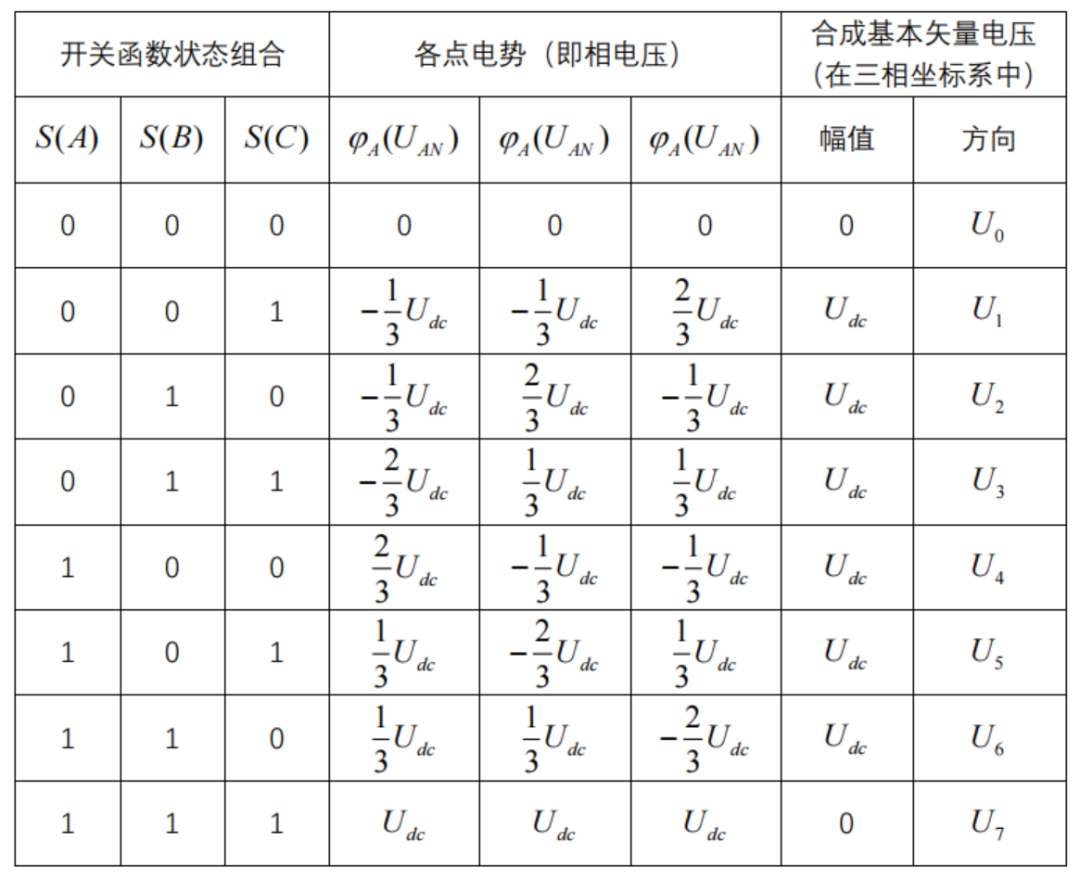
容易想到,通過控制開關管的狀態,可以合成6個方向中任意一個方向的矢量電壓;通過控制該狀態下開關管的PWM占空比,可以改變該方向的矢量電壓的幅值的有效值(占空比從0到100%對應矢量電壓有效值從0到Udc)。比如要合成一個方向和U4相同,幅值為Udc/2的矢量電壓,只需要控制G1的占空比為50%,G3,G5的占空比為0%即可;再比如要合成一個方向和U6相同,幅值為3Udc/4的矢量電壓,只需要控制G1,G3的占空比為75%,G5的占空比為0%即可。
在三相坐標系下,6個基本矢量電壓的幅值都為Udc,轉換到αβ兩相坐標系下,基本矢量電壓的幅值為2*Udc/3(為什么是2/3倍這個問題困擾了我好久才弄清楚了,下面簡單說明一下)。
以基本矢量電壓U1為例,U1(001)在abc三相坐標系下的幅值為Udc,他由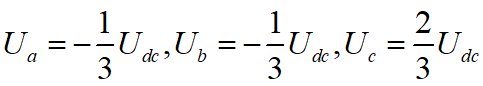 合成。經過clarke變換,得到在αβ兩相坐標系下的電壓
合成。經過clarke變換,得到在αβ兩相坐標系下的電壓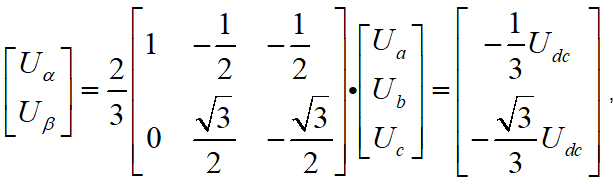 ,合成在兩相坐標系下的基本矢量電壓U1的幅值為
,合成在兩相坐標系下的基本矢量電壓U1的幅值為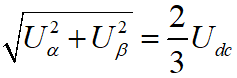 ,方向不變。因為我們判斷扇區和PID計算的輸出目標矢量電壓都是在兩相坐標系下進行的,故計算SVPWM也在兩相坐標系下進行。
,方向不變。因為我們判斷扇區和PID計算的輸出目標矢量電壓都是在兩相坐標系下進行的,故計算SVPWM也在兩相坐標系下進行。
下面的介紹都是在兩相坐標系下的,注意!
經過上面的步驟,已經能合成6個方向,幅值為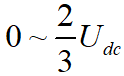 的基本矢量電壓了。接下來我們用這6個基本的矢量電壓,合成一個任意方向0-360°,任意幅值0~Umax的矢量電壓,即我們最終的目標矢量電壓,下面計算Umax的值。
的基本矢量電壓了。接下來我們用這6個基本的矢量電壓,合成一個任意方向0-360°,任意幅值0~Umax的矢量電壓,即我們最終的目標矢量電壓,下面計算Umax的值。
容易知道,通過這6個基本矢量電壓,能夠合成的最大旋轉圓形目標電壓,其幅值為正六邊形的內切圓的半徑,即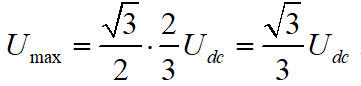 。
。
回顧一下數學知識:在一個平面內,兩個不共線的非零向量可以作為一個基底,兩個基底的線性組合可以合成該平面內任意方向和任意大小的第三個向量。(不懂沒關系,看下面就夠了)
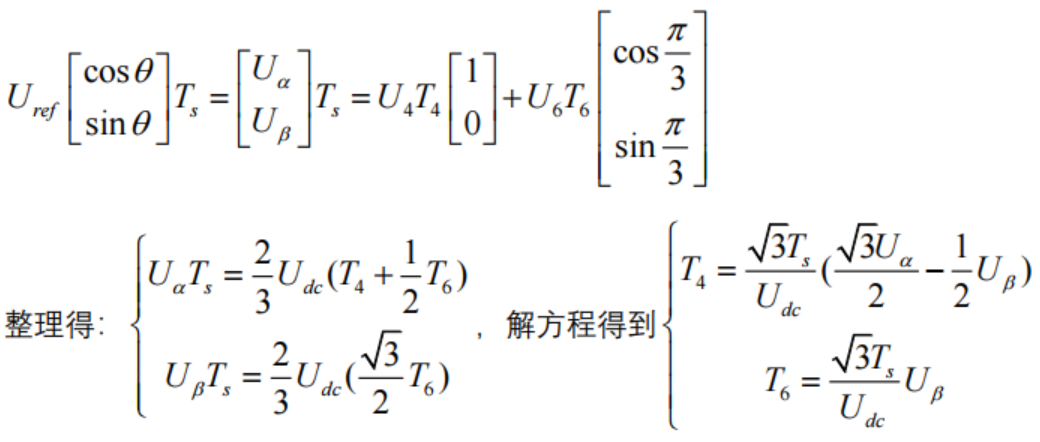
容易想到,任意一個目標電壓矢量,可以由該矢量所在扇區的相鄰兩個基本矢量電壓合成。比如扇區I的任意矢量電壓Us都可以由相鄰的U4和U6兩個基本矢量電壓合成。
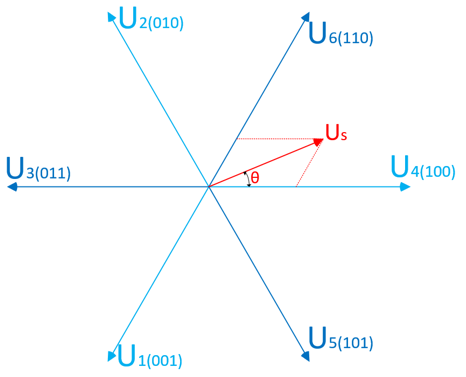
這里的Us就是坐標變換里的Uq和Ud的矢量和,(PS:在電機控制應用中,Uq由q軸電流環PI控制器計算輸出得到,同時d軸電流環還會計算輸出得到一個Ud,Ud滯后Uq90°)
然后回到坐標變換去了,另一篇文章有詳細講解[另一篇文章的鏈接],這里只簡單說明結果。
先是park逆變換,由期望輸出的Uq,Ud和當前的空間位置即角度θ[在電機控制里面這里是指電角度,并不是旋轉平面的角度(后面講電角度、電機極對數和旋轉角度的關系)],通過park逆變換計算Uα,Uβ。
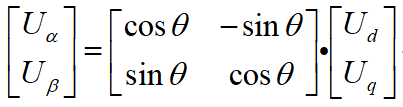
得到Uα,Uβ后,接著就是判斷所在扇區
2.2 扇區判斷:
目標矢量電壓Uref就是PI控制器計算的輸出Uq,Ud的矢量和,經過Park逆變換得到Uα和Uβ,空間矢量調制的第一步,就是由Uα和Uβ判斷目標空間矢量電壓所處的扇區。
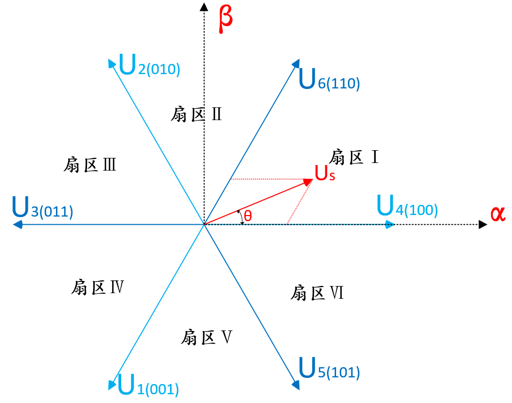
由以上矢量圖幾何關系分析可以得到,所在扇區和需要滿足的充分必要條件列表:

可以看出,決定扇區的基本變量有:
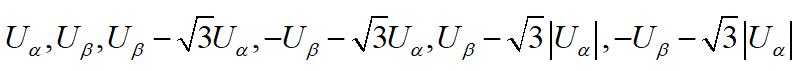
其中線性無關的只有三個(也可以取其他三個線性無關的):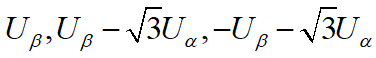

則(A,B,C)有8種狀態000,001,…………… ,111
其中(A,B,C)=(000)和(111)并不存在,另外6個狀態對應6個扇區,下面做簡單分析。
(A,B,C) =000時:
即U1<0,U2<0,U3<0,
即Uβ<0,由式2式3疊加得-Uβ<0,Uβ>0,和 式1沖突,故該狀態不存在。
(A,B,C)=001時:
即U1<0,U2<0,U3>0,
即Uβ<0,故電角度θ滿足:180<θ<360;
在Uβ<0的條件下,對Uα>0(270360)和Uα<0(180270)時分情況討論,并結合式2式3,即:
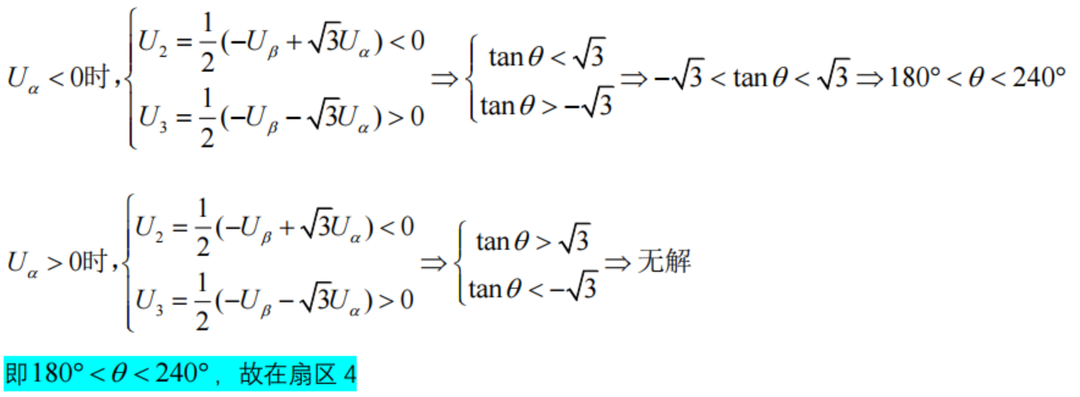
(A,B,C)=010時:
即U1<0,U2>0,U3<0,
即Uβ<0,故電角度θ滿足:180<θ<360;
在Uβ<0的條件下,對Uα>0(270360)和Uα<0(180270)時分情況討論,并結合式2式3,即:
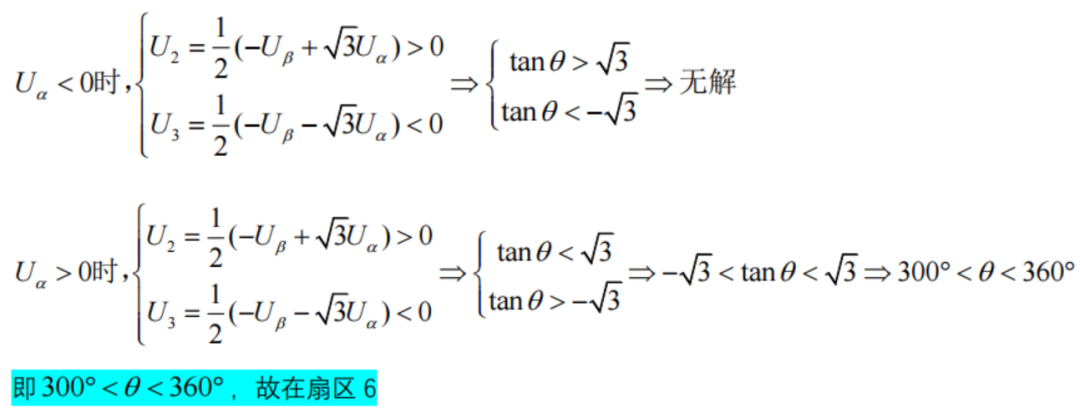
(A,B,C)=011時:
即U1<0,U2>0,U3>0,
即Uβ<0,故電角度θ滿足:180<θ<360;
在Uβ<0的條件下,對Uα>0(270360)和Uα<0(180270)時分情況討論,并結合式2式3,即:
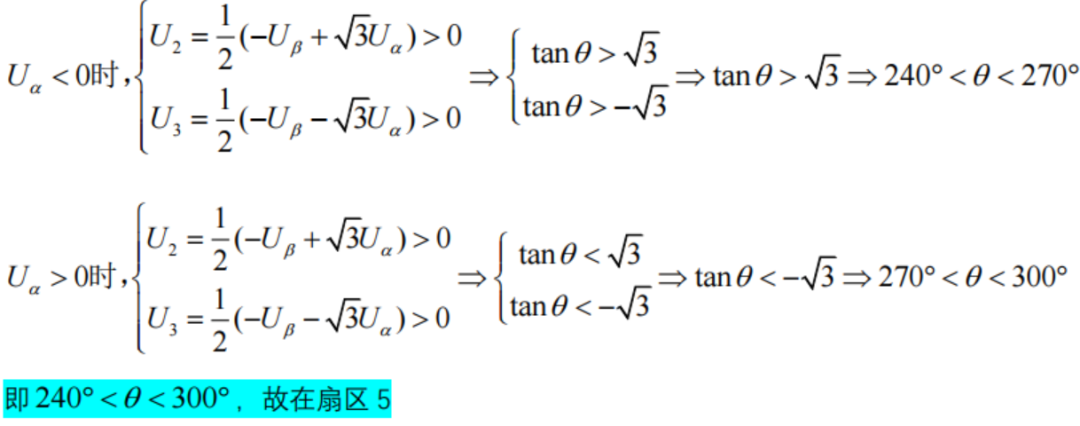
(A,B,C)=100時:
即U1>0,U2<0,U3<0,
即Uβ>0,故電角度θ滿足:0<θ<180;
在Uβ>0的條件下,對Uα>0(090)和Uα<0(90180)時分情況討論,并結合式2式3,即:
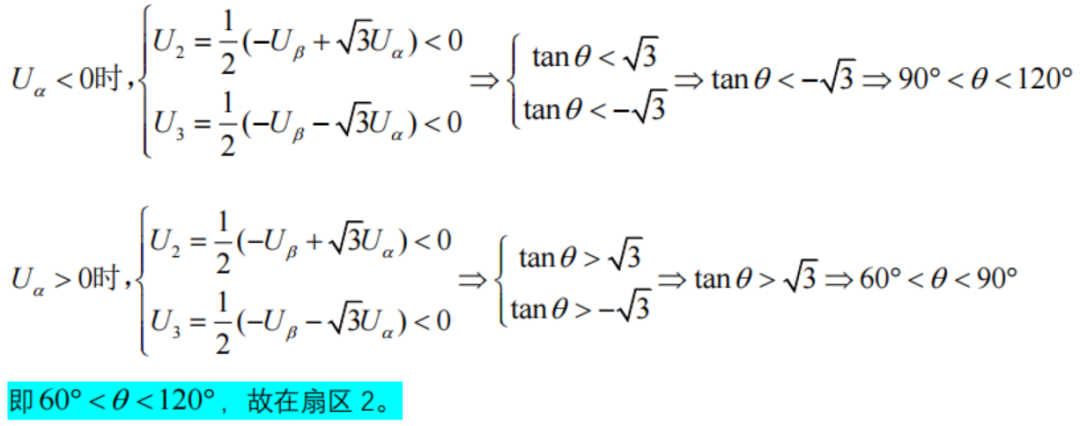
(A,B,C)=101時:
即U1>0,U2<0,U3>0,
即Uβ>0,故電角度θ滿足:0<θ<180;
在Uβ>0的條件下,對Uα>0(090)和Uα<0(90180)時分情況討論,并結合式2式3,即:

(A,B,C)=110時:
即U1>0,U2>0,U3<0,
即Uβ>0,故電角度θ滿足:0<θ<180;
在Uβ>0的條件下,對Uα>0(090)和Uα<0(90180)時分情況討論,并結合式2式3,即:
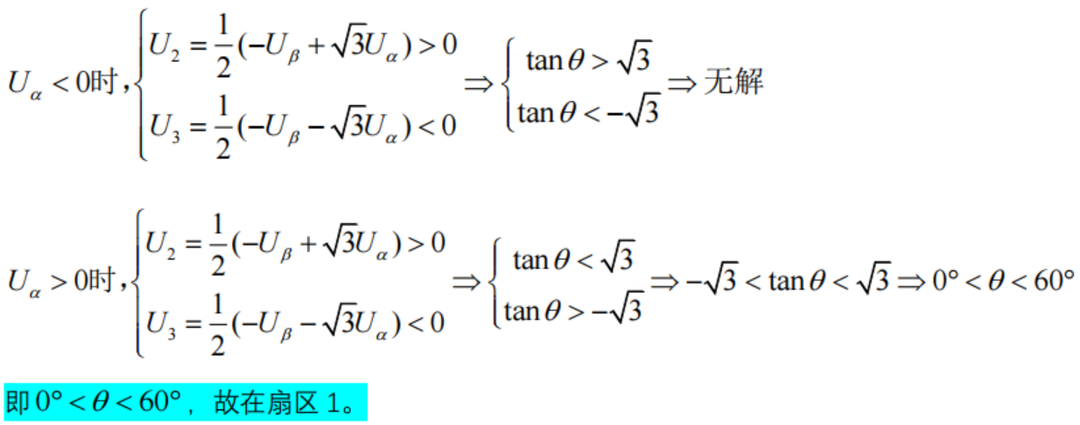
(A,B,C) =111時:
即U1>0,U2>0,U3>0,
即Uβ>0,由式2式3疊加得-Uβ>0,Uβ<0,和 式1沖突,故該狀態不存在。
綜上,可以列出(A,B,C)的值和所對應的扇區關系如下表;
| (A,B,C) | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| 所在扇區 | 無 | 4 | 6 | 5 | 2 | 3 | 1 | 無 |
| N=4C+2B+A | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
| N=4A+2B+C | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
然后在程序里里面查表,根據計算的N查找對應的扇區。
-
電壓
+關注
關注
45文章
5567瀏覽量
115604 -
SVPWM
+關注
關注
14文章
614瀏覽量
90583 -
矢量
+關注
關注
0文章
95瀏覽量
23738
發布評論請先 登錄
相關推薦
必學的BLDC電機控制算法——FOC簡述
FOC電機控制相關資料下載
實現電機SVPWM旋轉的FOC頻率大概是多少
【硬聲推薦】電機FOC控制視頻合集
簡述FOC電機控制之SVPWM原理(下)
電機foc是什么意思 svpwm和foc的區別
電機控制---SVPWM扇區判斷的實現以及推導過程

電機控制--FOC的優勢

BLDC電機控制算法之FOC簡述




 簡述FOC電機控制之SVPWM原理(上)
簡述FOC電機控制之SVPWM原理(上)











評論