大家對電機的認識可能就是高中課本里的交變電流章節的例子,電刷+外磁場+通電線圈。這是最經典的有刷電機。但是今天咱們談論的是另一種更高效、性能更好的電機——無刷電機。
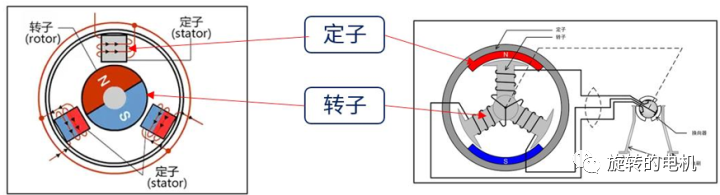
如圖是無刷電機的等效模型。內外兩個灰色的輪子一個是定子,一個是轉子(具體哪個是定子哪個是轉子根據電機類型有所不同)。此時轉子和定子是完全重合在一起的,沒有扭矩的存在。
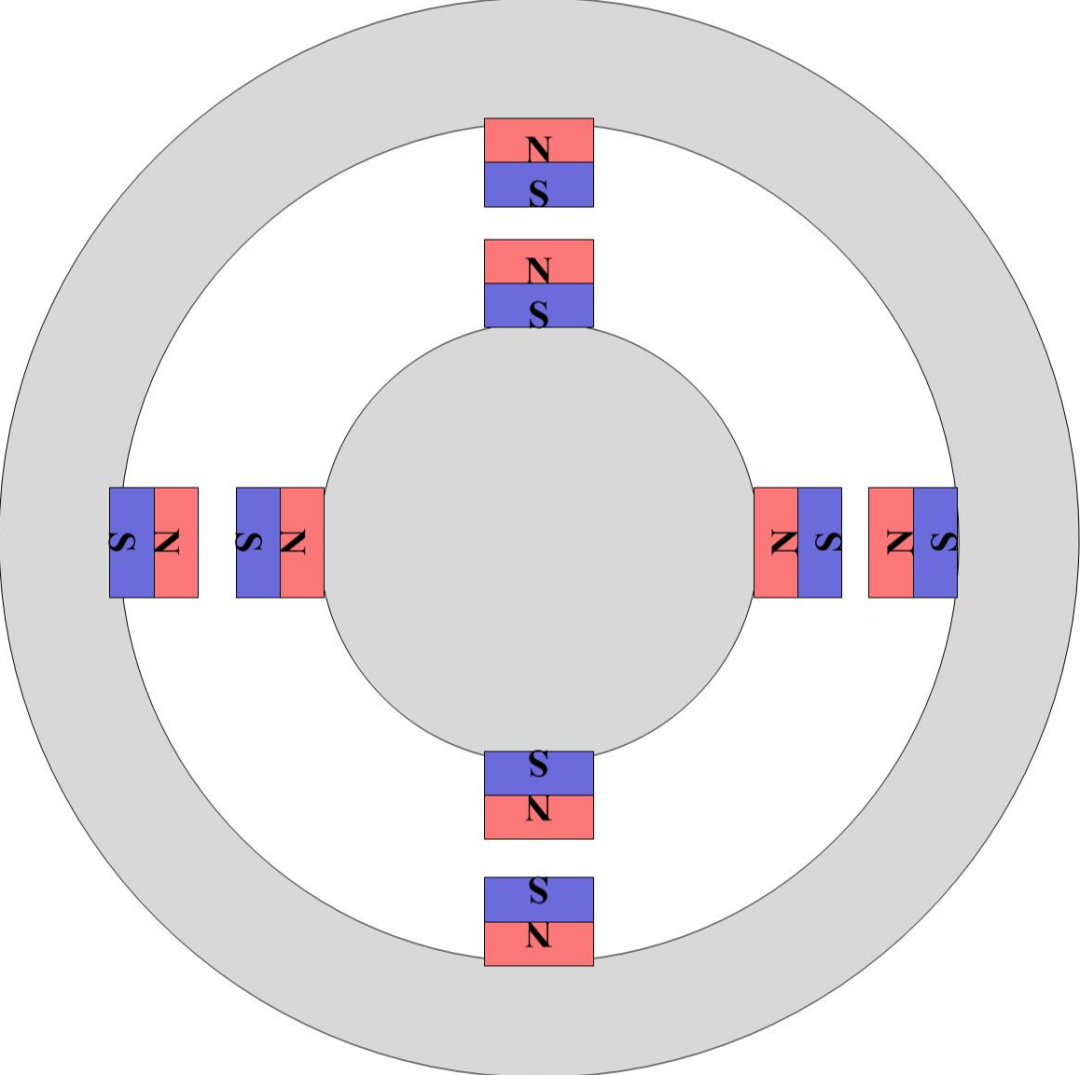
咱們定性地看,當外部的定子磁場扭轉一個角度時,內部的轉子會跟著旋轉。這個時候就存在扭矩了。
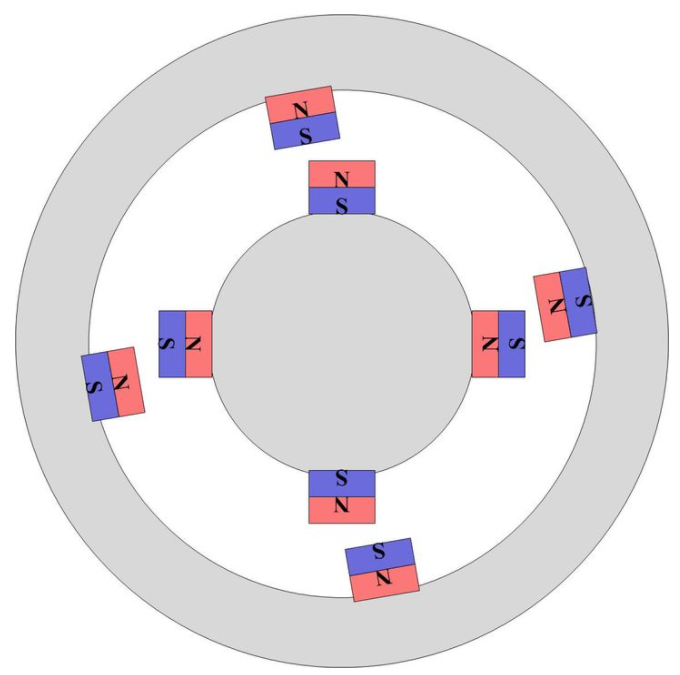
扭矩的大小如何衡量?如下圖所示
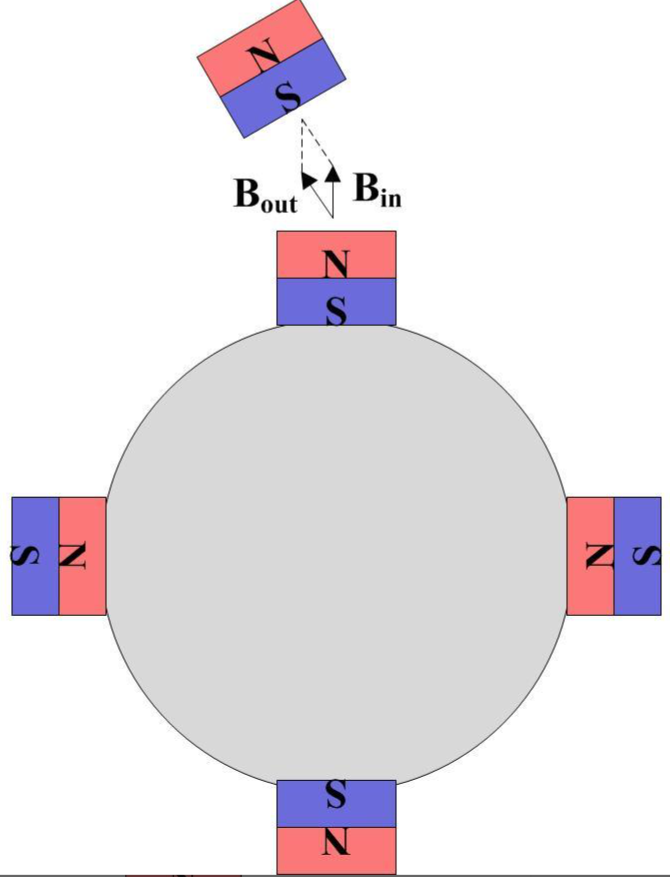
所有的電機扭矩的大小正比于內外兩個磁場的叉乘,即圖中圍出的平行四邊形的面積。可見兩個磁場重合時,叉乘為0,扭矩也為0,和之前的直觀認知相符合。顯然,當兩個磁場呈90度時,平行四邊形面積最大,此時的扭矩也最大。
實際的無刷直流電機(BLDC)或永磁同步電機(PMSM)通常用三相****交流繞組線圈充當定子,永磁體作為轉子。我們希望通過電路控制定子繞組的輸出,使之能夠能產生一個大小盡可能恒定的旋轉磁場,讓轉子和定子的扭矩達到最大值。
( 具體為何使用三相線圈的相應電路分析筆者在此不予贅述 )
這就是FOC(Field-Oriented Control)矢量控制要完成的目標
FOC(Field-Oriented Control),即磁場定向控制,也稱矢量變頻,是近幾年較為主流的高效控制無刷直流電機(BLDC)和永磁同步電機(PMSM)的選擇。
要實現這樣的功能,我們可以簡單分為以下分為兩步
- 如何產生一個可控的旋轉磁場
- 如何讓這個磁場大小穩定
如何產生一個可控的選擇磁場
要得到一個恒定大小的旋轉磁場很容易。當今主流的BLDC和PMSM電機定子均采用的是三相繞組,即各個繞組上的交流信號就是相位互差120°的信號。根據三相電機的結構,我們可以 將一個恒定大小的旋轉電壓矢量分解到相位互差120°的方向上 。如下圖
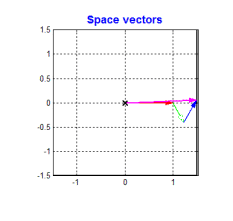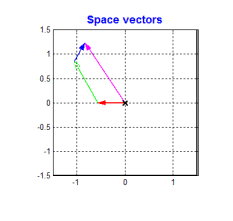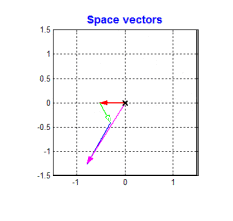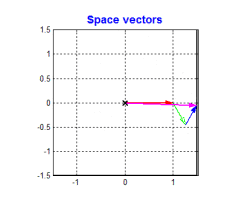
從上圖可以看到,只要控制電機的三個繞組產生相位互差120°的大小隨著時間按正弦規律變化的3個分矢量,就可以得到我們想要的旋轉磁場
如何讓磁場大小穩定
然而,在實際的電機控制中,由于齒槽效應、磁通畸變等因素,電機的轉矩會產生大量的波動,需要不斷地對控制信號做出修正。但是當電機轉速較高時,電流環控制器必須跟蹤頻率不斷提高的弦波信號,而且還要克服振幅和頻率不斷提高的電機反電動勢。在這樣的情況下,想要直接通過維持三路正弦信號得到旋轉平滑、大小穩定并且一直保持和轉子磁場方向垂直的磁場難以實現。
我們重新回到一開始的磁場叉乘。我們發現電機的轉矩 只與 平行于內磁場方向(稱d軸)的磁場分量 和 垂直于內磁場方向的分量(稱q軸) 有關(如下圖)。
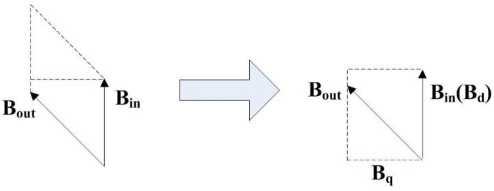
現在對于電機扭矩大小的控制就變成了q軸和d軸大小乘積的控制。在電機中,d軸上內磁場的大小是永磁鐵產生的,是恒定的;我們對外磁場的控制實質上變成了q軸上的分量大小控制+外磁場的角度。
我們可以使用編碼器測量轉子的內磁場角度,然后根據內磁場的角度用電機繞組產生對應的外磁場。
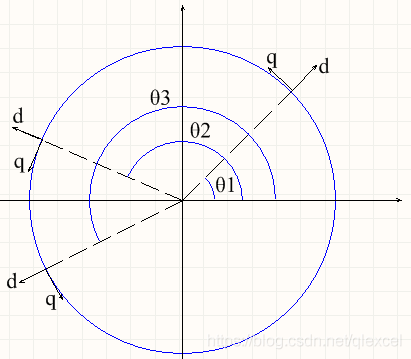
如上圖所示,如果轉子的電角度在θ1,則我們就要在θ1處產生d、q軸大小的外磁場。如果轉子的電角度在θ2,則我們就要在θ2處產生d、q軸大小的外磁場。
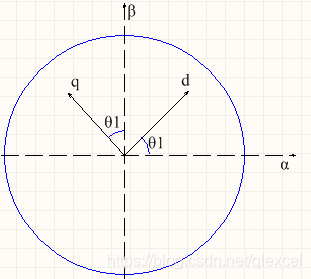
我們把角度θ1的情況單獨提出來,把它移到原點去,然后把x、y軸重命名為α,β。根據空間矢量的關系,我們可以把q、d軸的大小分解到α,β軸上。這個過程就是所謂的“反 帕克(Park)變換 ”。
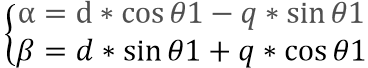
若d=0
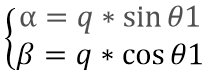
其實得到的結果很簡單,它就是用了互差90°的正弦信號得到了大小恒定的旋轉磁場。
控制電機只需要4步:
第一步,選定q、d軸的值(比如q=2,d=0)。
第二步,用編碼器測量轉子電角度(內磁場角度)。
第三步,用上面的式子計算α,β值。
第四步,把α,β輸入到專門的處理電路SVPWM,輸出三相信號驅動電機
(對SVPWM的介紹可以參考這篇CSDN文章。
http://t.csdn.cn/bFZZc
可以大概理解為在PWM輸出的基礎上增加若干花里胡哨的風騷處理( ̄▽ ̄)~*)
繞了這么多彎彎,我們終于讓電機轉起來了。大家看到這里可能會說:“這是在折騰啥?(╬ ̄皿 ̄)不還是最后轉成三個相差120°的正弦信號了嗎?”
(* ̄︶ ̄)
沒錯,到目前為止只是在繞彎子。但是關鍵在于下面幾個問題:
1、我怎么知道電機有沒有按照我設定的q、d值來轉呢?
2、設定q、d值只能控制扭矩,我如果要控制電機的速度和位置怎么辦?
這些問題都是上面那個開環系統解決不了的,這個時候就要引入閉環了。
我們先測量電機的3相電流。電機的信號如下圖所示(把相差120°的電信號看成同一個旋轉向量在三個相差120°坐標軸上的投影)
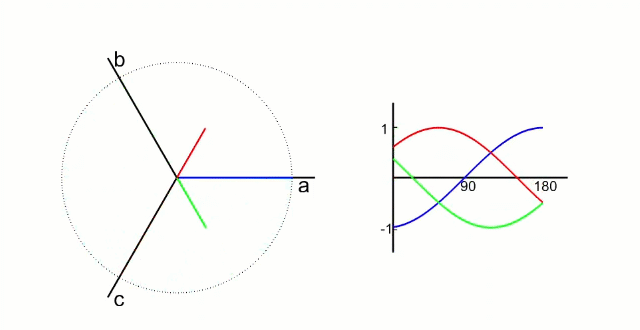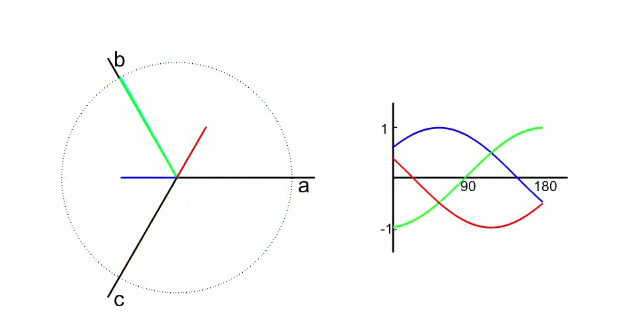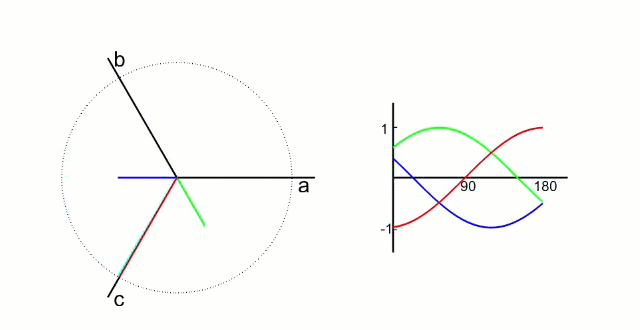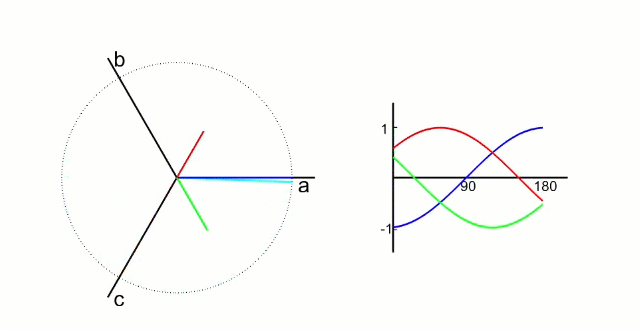
根據我們之前的理論,我們需要的是兩個互差90°的磁場。這里咱們又使用一個變換,把三個分磁場變換成α、β方向上的兩個分磁場。這個叫做“ 克拉克(Clarke)變換 ”。
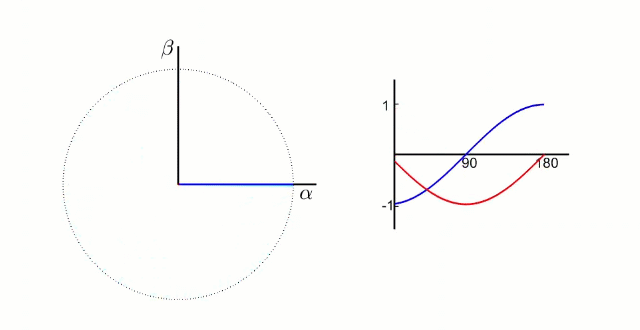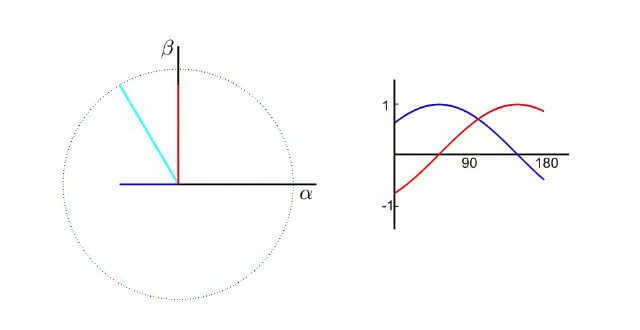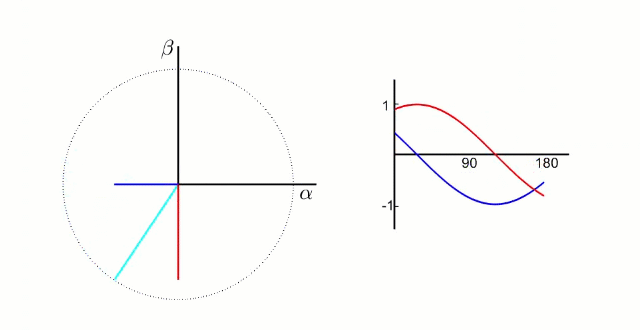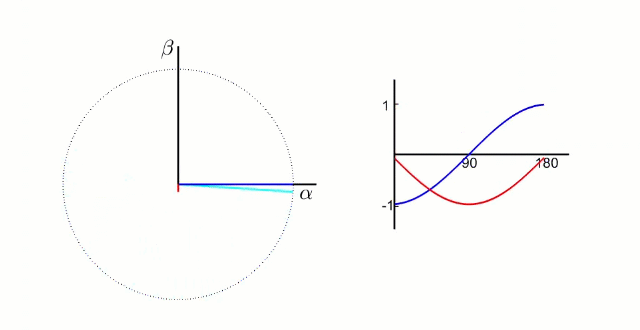
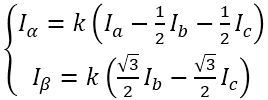
(變換中有一個系數k,一般取2/3,有興趣可以去搜索了解)
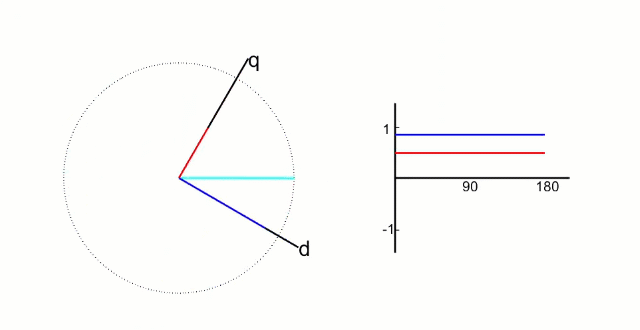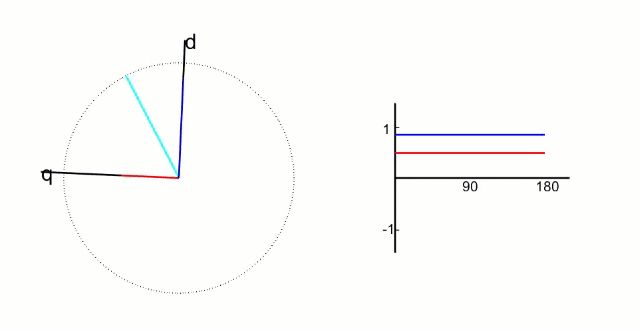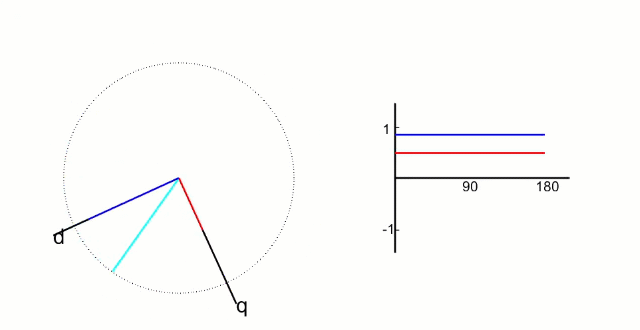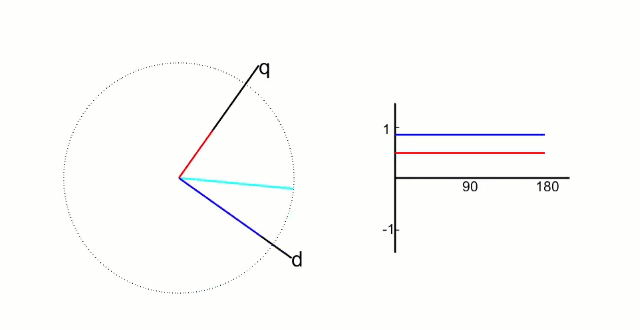
再把α,β軸上的值映射到旋轉的q、d軸上,得到此時電機實際的d值和p值。這是之前反Park變換的逆過程, “ 帕克Park變換”
我們把測量到的d、q軸值與我們設定的值做對比,通過PI算法消除誤差,再重新通過之前的流程輸入到SVPWM中,這就完成了一個閉環控制,可以對定子磁場的做動態修正了。因為控制d、q是在控制電流值,所以這個環路叫做電流環。
總結一下,電流環的邏輯是這樣的
- 設置d0、q0值(目標值),經過反Park變換得到Iα和Iβ,輸入給SVPWM執行
- 測量q、d軸的值:測量電機的相電流(測量兩相,通過Ia+Ib+Ic=0得到第三相),然后通過Clarke變換得到Iα和Iβ,然后通過park變換得到q、d軸的值。
- 把測量到的d、q軸值與我們設定的d0、q0做對比,進行PID處理。(目標是讓測量值與我們的設定值相同)
- 調整d、q值輸出,回到1.
除了電流環之外,由于d、q是直流信號, 我們通過d、q也可以更輕松地控制電機的 轉速和旋轉位置 。
比如設定電機轉速為1000Rpmin,編碼器測得當前轉速為500,同樣用PID算法增大q值就可以加大扭矩,讓電機的速度加快了。這個環路叫 速度環, 即在電流環的外面加一層,改變q、d設定值來改變速度。
當然我們也可以加上 位置環 ,通過對速度的積分可以得到電機的位置,計算位置誤差進行PID調整。
看ヾ(??▽?)ノ,我們把對三相交流正弦信號的控制轉換成了對直流信號d,p的控制,這樣優勢就出來了,很nice~
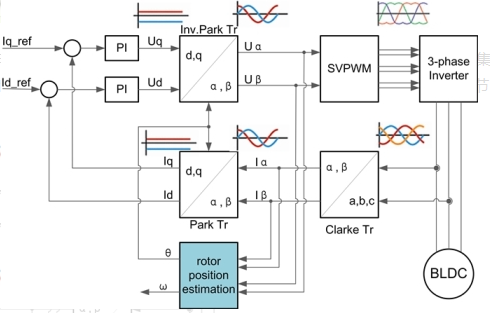
FOC控制簡圖
其他
除了FOC之外,還有其他控制電機的方法,比如梯形波式控制、弦波控制等。詳細介紹可以參考這篇文章
http://t.csdn.cn/7UsSi
簡單概括,弦波式換相能讓電機在低速下運轉平穩,但在高速運轉下效率卻大大降低;而梯形波式換相在電機高速運轉下工作比較正常,但在電機低速運轉下,會產生力矩的波動。因此,矢量控制是對無刷電機的最佳控制方式~
-
磁場
+關注
關注
3文章
856瀏覽量
24182 -
電機
+關注
關注
142文章
8930瀏覽量
145090 -
無刷電機
+關注
關注
57文章
823瀏覽量
45764
發布評論請先 登錄
相關推薦
直流無刷電機的工作原理的詳細資料簡介
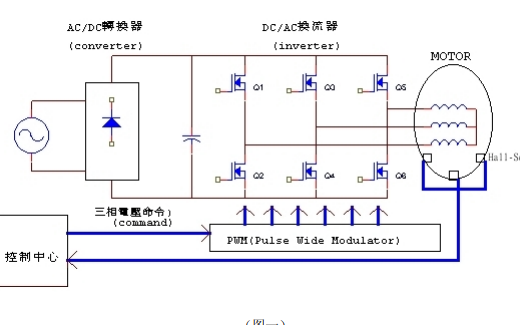
直流無刷電機的工作原理





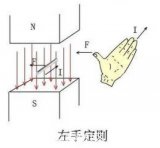
 無刷電機的工作原理與扭矩
無刷電機的工作原理與扭矩











評論