若無法得到車輛在地圖上的準確位置及周圍障礙物的位置,那么自動駕駛便無從談起。因此在自動駕駛領域,對車輛自身及周圍物體的精確定位至關重要。然而現實環境中存在各類噪聲,無論是激光雷達、慣性導航器件甚至衛星定位系統都無法得到完全真實的車輛位置信息。為了應對此類情況,便需要采用濾波算法來過濾觀測噪聲,以得到更加精確的定位結果。
1
何為卡爾曼濾波
在各類濾波定位算法中,卡爾曼濾波是最為知名的一種。為了解決阿波羅登月計劃中的航天器定位及噪聲干擾問題,這種算法最初在1963年由匈牙利數學家魯道夫·卡爾曼所提出[1]。卡爾曼濾波不僅將過去類似的基于系統可觀性與可控性的控制方法做出了系統化的整理,并且在嚴格的數學意義上證明這種方法在線性系統的高斯隨機噪聲過濾方法中具有最優性。
卡爾曼濾波的簡單舉例
為了更好的理解卡爾曼濾波的基本原理,本文首先對卡爾曼濾波的原理進行舉例說明。
試想一下,假設你要憑借地圖從A地前往B地,你要如何知道自己的位置呢?
首先,你可以通過自己的腳程判斷,“A地到B地大約10公里,憑我的腳程大約需要步行3小時左右”。
其次,還可以通過路牌和手里的地圖判斷,“這個路牌上寫著到了D鎮,地圖上顯示D鎮應該在距離B地還有3公里的地方”。
然而不論是地圖還是腳程估算都存在的較大誤差,此時我們為了得到更準確的所處位置,可以結合地圖與腳程來對當前位置進行估算。比如:A地到B地大約10公里,憑我的腳程大約需要步行3小時左右,目前已經走了2小時,那么我推測再過不久就可以到達D鎮,此時再對照地圖上D鎮的位置,就可以得到更加精確的位置信息,同時通過對比實際到達D鎮的時間,還可以反過來修正對于自己腳程的估計誤差。

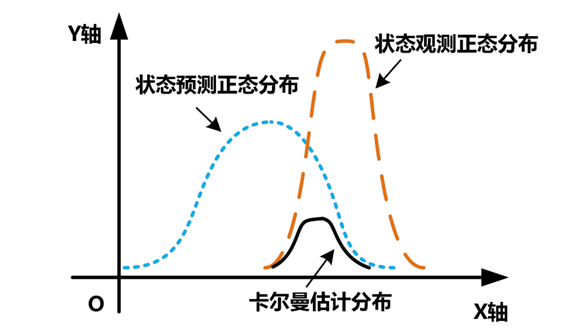
圖1 卡爾曼濾波原理示意圖
2
卡爾曼濾波的基本公式
根據上一節的例子,我們就可以引出卡爾曼濾波的基本公式:
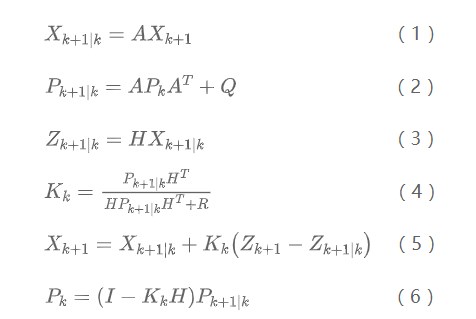
前兩步是根據上一個最優估計值得出此刻的估計值和估計值的協方差,緊接著就可以得到此刻的最優估計值和最優估計值的協方差,然后利用此刻的最優估計值和最優估計值的協方差進行下一個迭代。
公式詳解
看起來有點多,但是實際上非常緊湊,推理非常嚴謹,接下來將對上述六個公式進行詳細解釋。
式(1)為系統的狀態預測公式,通過上一時刻的位置對當前時刻的位置進行了推測,但是由于過程噪聲的存在,這個推測出的位置不完全符合真實情況。
式(2)為系統的狀態誤差傳遞,類似式(1),是基于上一時刻位置可能分布的范圍對當前時刻的可能分布范圍做出預測,Q是可能的估計誤差。
式(3)則是當前時刻觀測量的預測值,代表我們根據預測出的狀態,推測出我們將會觀測到的讀數,并非真正的讀數。
式(4)為卡爾曼增益的計算方法,其物理意義為狀態預測誤差與觀測誤差的比例關系。
式(5)則為對系統狀態的更新,這個公式可以分為兩方面看,后半段的代表實際讀數與推測讀數之間的差值,被稱為殘差。使用式(4)求得的卡爾曼增益與殘差相乘,可以得到對狀態預測的修正量,最終式(5)可以得到圖1中的卡爾曼位置估計更新。
式(6)則為對位置估計的分布估計,可以作為下一時刻式(2)的初值使用。
實例說明
假設車輛在進行勻速運動,則可以設置其遞推運動模型為:
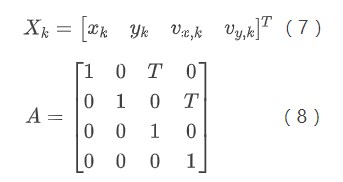

最后,按順序將上述變量帶入式(4)、(5)、(6)即可實現對位置坐標的更新,同時得到的結果還可以作為下一步迭代的初值。
3
非線性卡爾曼濾波
雖然卡爾曼濾波已經在數學上被嚴格證明具有最優性,然而卻無法處理非線性系統。針對這種情況,現有的解決方法分為兩種,分別是基于泰勒展開進行線性化近似的擴展卡爾曼濾波[2]和基于多點采樣進行均值方差近似的無跡卡爾曼濾波。
擴展卡爾曼濾波
擴展卡爾曼濾波通過一組式(11)所示的n階泰勒線性展開式近似表達非線性函數:

如圖2所示,其階數越高,近似程度越高。
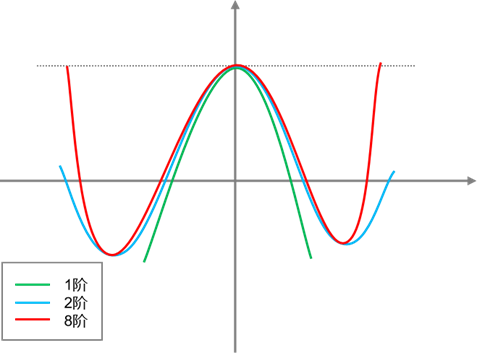
圖2 各級泰勒展開線性化效果
這種方法具有計算復雜度低、技術成熟的優點,因此,目前在工程中被廣泛使用。然而由于泰勒展開式的復雜度隨著階數呈指數增長,往往在實際應用中很難實現三階以上的泰勒展開,這導致了這種線性化方法存在較大的截斷誤差,因此限制了算法的估計精度,并且在非線性程度較高的系統中容易發散。
無跡卡爾曼濾波
無跡卡爾曼濾波則通過對非線性函數在目標時刻的均值與方法進行相似擬合來實現線性化近似的(如圖3所示),這種方法被稱為無跡變換(UT變換)。
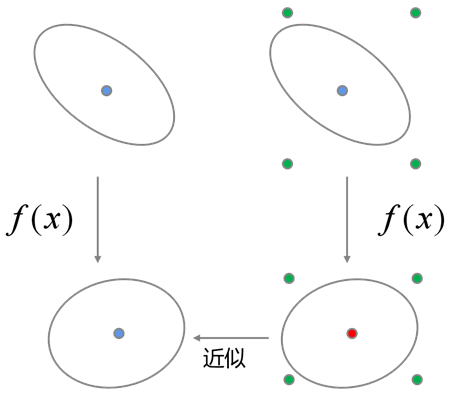
圖3 無跡變換原理
UT變換已被Julier和Uhlmann[3]證明具有不低于三階泰勒展開的線性化精度,因此基于UT變換的無跡卡爾曼濾波具有相對于擴展卡爾曼濾波更高的精度,同時其均值與方差的擬合不會受函數非線性化程度的影響,因此可以適用于更為非線性的系統。然而,由于使用無跡卡爾曼濾波需要設置較多參數,并且計算負擔較重,因此在實際工程中仍然不能完全取代擴展卡爾曼濾波。
基于上述原因,目前在非線性系統上需要根據系統特征與實際需求對濾波器的性能做出取舍,選擇最合適的方法進行計算。
4
SLAM中的卡爾曼濾波與圖優化
由于SLAM(Simultaneous Localization and Mapping,同步定位與建圖)中對于特征點、路徑與移動體的定位同卡爾曼濾波的適用范圍十分吻合,因此,早期SLAM中通常采用卡爾曼濾波在后端對輸出進行優化。隨著計算能力的不斷加強,近年來基于圖優化的SLAM方法也逐漸占據了一席之地。
從應用角度分析,基于卡爾曼濾波和基于圖優化的SLAM方法各有優勢。
卡爾曼濾波具有計算速度快、系統簡單的優點,但由于其對后端輸出的優化僅基于相鄰兩個馬爾可夫鏈的信息進行一次迭代,因此在精度上有所欠缺,更適用于高動態且對精度要求不高的場合。
相對的,因子圖優化可以統籌全局信息以對各位姿輸出進行優化,并且優化迭代次數可以人為設置,可以得到更加精確的后端輸出。正因如此,其每次迭代及出現新的輸出時都需要對全局進行計算,使得計算負擔大幅增加。所以一般情況下,基于圖優化的SLAM僅適用于對于精度要求極高的特殊場合。
隨著技術的發展,這兩種路線也在分別補齊自身的固有短板。
如基于濾波的SLAM中引入了迭代擴展卡爾曼濾波,將最小二乘法與卡爾曼濾波相結合,對誤差而不是位姿進行優化,實現了更高的定位精度,并且可以實現動態設置迭代次數,代表算法有LINS和Fast-Lio等。
反之,為了應對圖優化“牽一發而動全身”的問題,最近比較熱門的LIOM和LIO-SAM等算法引入了動態滑窗和關鍵幀機制,僅對少數相關的時刻進行聯系,有效降低了冗余計算,并且引入了IMU預積分等技術,進一步削減系統的計算負擔,獲得了更快的動態響應時間。
總體來看,基于圖優化的SLAM是未來的發展趨勢,而目前產品化的SLAM設備仍以濾波為主流。
審核編輯:劉清
-
濾波器
+關注
關注
160文章
7743瀏覽量
177712 -
SLAM
+關注
關注
23文章
419瀏覽量
31788 -
卡爾曼濾波
+關注
關注
3文章
162瀏覽量
24636 -
GPS信號
+關注
關注
0文章
25瀏覽量
9399
原文標題:基于卡爾曼濾波的定位算法
文章出處:【微信號:gh_c85a8e3c0f2a,微信公眾號:賽目科技】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 淺析基于卡爾曼濾波的定位算法
淺析基于卡爾曼濾波的定位算法


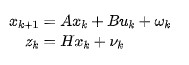











評論