本文翻譯自關(guān)于高斯濾波器響應(yīng)和逼近的文章(1959),作為早期高斯濾波器的實(shí)現(xiàn)相關(guān)論文,分析和設(shè)計(jì)方法非常經(jīng)典,值得精讀。
英文原文。
關(guān)于高斯濾波器的響應(yīng)和逼近(On the Response and Approximation of Gaussian Filter)
摘要
本文討論了一種濾波器,其幅頻響應(yīng)特性為,其中是頻率的函數(shù),是與濾波器帶寬相關(guān)的常數(shù)。該濾波器的幅度響應(yīng)曲線(xiàn)具有高斯概率函數(shù)的形狀,結(jié)果表明,相位響應(yīng)曲線(xiàn)基本上是線(xiàn)性的。以前的研究人員已經(jīng)表明,這種濾波器具有出色的瞬態(tài)特性,從某種意義上說(shuō),它是瞬態(tài)信號(hào)的最佳濾波器。本文討論了其對(duì)脈沖和階躍函數(shù)的響應(yīng)。給出了一種設(shè)計(jì)高斯濾波器的逼近方法,并給出了這種高斯濾波器逼近的實(shí)際響應(yīng)測(cè)試結(jié)果。
I. 介紹
對(duì)于任何輸入波形,當(dāng)網(wǎng)絡(luò)輸出的波形與輸入的波形相同時(shí),可以說(shuō)網(wǎng)絡(luò)具有理想的瞬態(tài)響應(yīng)。只有純電阻網(wǎng)絡(luò)才有這樣的響應(yīng)。一個(gè)濾波器,就其應(yīng)用本質(zhì)而言必須是具有非恒定頻率響應(yīng)的,所以是不能具有這樣理想的響應(yīng)。濾波器的帶寬越窄,其瞬態(tài)響應(yīng)的失真就越大。因此,具有最小幅度響應(yīng)展寬(amplitude-response spread)和波形失真(distortion)組合的濾波器可稱(chēng)為瞬態(tài)“最佳”濾波器。
此處選擇脈沖函數(shù)和階躍函數(shù)作為代表性輸入波形來(lái)描述高斯濾波器的特性,因?yàn)椋?) 這些是瞬態(tài)分析相關(guān)文獻(xiàn)中最常討論的函數(shù),2) 一旦已知脈沖或階躍響應(yīng),線(xiàn)性濾波器對(duì)任何波形的響應(yīng)都可以通過(guò)疊加定理獲得。如果帶通濾波器相對(duì)于其中心頻率具有低通模擬和相對(duì)較窄的帶寬,則可以假設(shè)帶通濾波器對(duì)濾波器中心頻率處的波的包絡(luò)響應(yīng)與模擬低通濾波器對(duì)具有包絡(luò)形狀的波的響應(yīng)相同。為方便起見(jiàn),本文主要考慮低通高斯濾波器的響應(yīng)。然而,結(jié)果也適用于上述條件下的帶通高斯濾波器。附錄Ⅱ描述了一個(gè)實(shí)用的高斯帶通濾波器的設(shè)計(jì)。
低通高斯濾波器的頻率響應(yīng)特性可以由下式定義:
其中是與帶寬相關(guān)的常數(shù)。這種濾波器的頻率響應(yīng)曲線(xiàn)的形狀如圖1所示,與高斯概率分布曲線(xiàn)相同。如下所示,高斯濾波器具有出色的瞬態(tài)響應(yīng)特性,并且可以相對(duì)容易地進(jìn)行函數(shù)逼近。
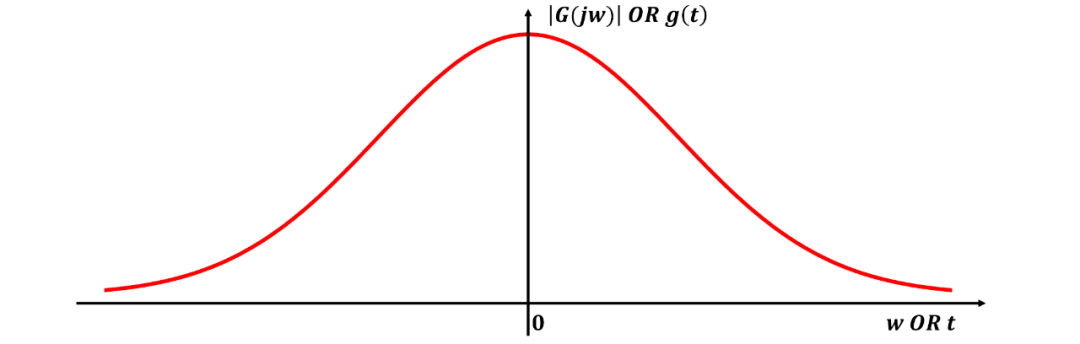
圖1 高斯響應(yīng)曲線(xiàn)
II. 脈沖響應(yīng)
如果式(1)的低通高斯濾波器的輸入信號(hào)是單位脈沖,則時(shí)域輸出由下式給出
其具有圖1所示的高斯形狀,與濾波器的幅度響應(yīng)特性曲線(xiàn)相同。通過(guò)圖2所示的帶通濾波器的脈沖響應(yīng)波形可以看到,該帶通濾波器的形狀近似為高斯曲線(xiàn),其具體設(shè)計(jì)將在第 V 節(jié)中進(jìn)行描述。請(qǐng)注意,是曲線(xiàn)包絡(luò)具有圖1的形狀。
讓我們來(lái)定義:a) 由于濾波器而引起的脈沖失真為時(shí)間響應(yīng)展寬(time-response spread) 的均方值
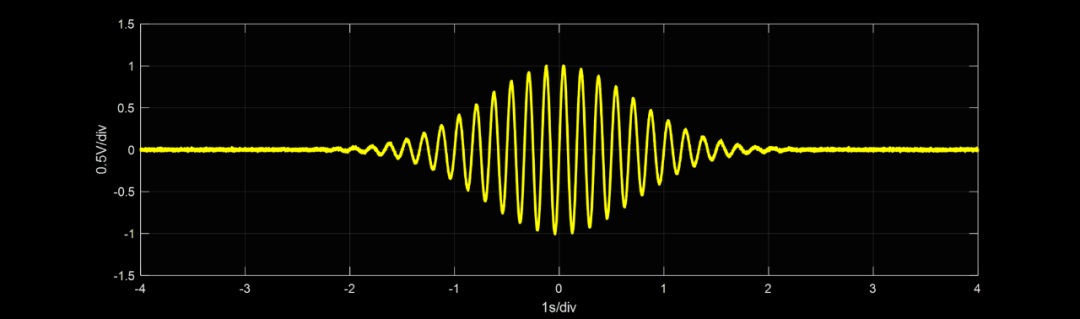
圖2 帶通濾波器(圖8)的脈沖響應(yīng)示波器顯示圖
b) 濾波器的幅度響應(yīng)展寬(amplitude-response spread) 的均方值
最佳的瞬態(tài)濾波器應(yīng)該具有最小的時(shí)間和幅度響應(yīng)展寬的組合。如果最優(yōu)性標(biāo)準(zhǔn)是
或者是
其中是加權(quán)常數(shù)。具有式(5)形式的方程已由諾伯特·維納(N. Wiener, 譯注:維納是控制論創(chuàng)始人, 維納濾波器發(fā)明者)求解得到。和具有式(6)形式的方程由 A. Gabor(譯注: 這里應(yīng)該是D. Gabor即Dennis Gabor,就是大名鼎鼎的因全息技術(shù)而獲得諾貝爾獲的丹尼斯·加博爾)求解得到。
現(xiàn)實(shí)工程實(shí)踐中出現(xiàn)的許多脈沖在形狀上都非常接近高斯曲線(xiàn)。通過(guò)高斯濾波器后的高斯脈沖將保持其高斯形狀,但會(huì)在時(shí)間上展寬(spread out)。這可以表示如下:
讓高斯輸入脈沖由下式給出
其中是決定脈沖展寬的常數(shù)。然后
從式(1)和式(8)可以得出
然后
很明顯,任何數(shù)量的高斯濾波器級(jí)聯(lián)都將具有高斯的組合傳遞函數(shù)(combined transfer function)。
III. 階躍響應(yīng)
階躍函數(shù)是脈沖函數(shù)的積分。鑒于系統(tǒng)假定是線(xiàn)性的,高斯濾波器對(duì)單位階躍的響應(yīng)是此類(lèi)濾波器對(duì)如式(2)所給出的單位脈沖響應(yīng)的積分,
該等式的曲線(xiàn)繪制在圖3中。我們所構(gòu)造的高斯帶通濾波器對(duì)中心頻率調(diào)制的階躍函數(shù)的響應(yīng)波形如圖4所示。請(qǐng)注意,曲線(xiàn)包絡(luò)具有圖4的形狀。圖3的響應(yīng)特性顯示無(wú)過(guò)沖(no overshoot)、無(wú)振鈴(no ringing)、無(wú)拖尾(no smear),并且波形關(guān)于其半值點(diǎn)完全對(duì)稱(chēng)。對(duì)稱(chēng)性是高斯濾波器線(xiàn)性相位響應(yīng)的結(jié)果。此外,這意味著過(guò)渡是最陡峭的。低通高斯濾波器的(帶寬上升時(shí)間)乘積為 0.343,如果響應(yīng)有非常小或沒(méi)有過(guò)沖,這非常接近可能的最低值。此(帶寬上升時(shí)間)乘積的計(jì)算在附錄 I 中給出。簡(jiǎn)單的 RC 低通網(wǎng)絡(luò)的 (帶寬上升時(shí)間) 乘積為0.35非常接近高斯濾波器的。然而,高斯濾波器的幅頻響應(yīng)曲線(xiàn)的截止頻率的滾降要高得多。事實(shí)上,需要使用無(wú)限多個(gè)級(jí)聯(lián)的 RC 網(wǎng)絡(luò)才能獲得高斯響應(yīng)曲線(xiàn)。
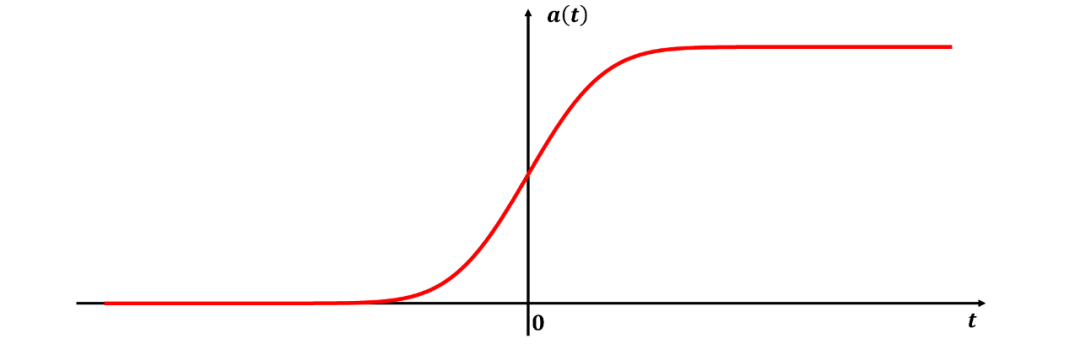
圖3 高斯濾波器階躍響應(yīng)
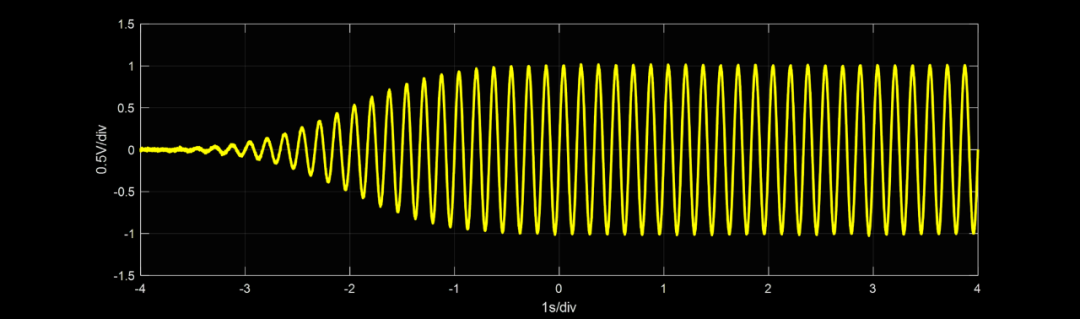
圖4 帶通濾波器(圖8)的階躍響應(yīng)示波圖
在通帶中具有零衰減和在阻帶中具有無(wú)限衰減的矩形濾波器有時(shí)被稱(chēng)為“理想”濾波器(ideal filter)。這種低通濾波器的階躍響應(yīng)是如圖5所示的函數(shù)。
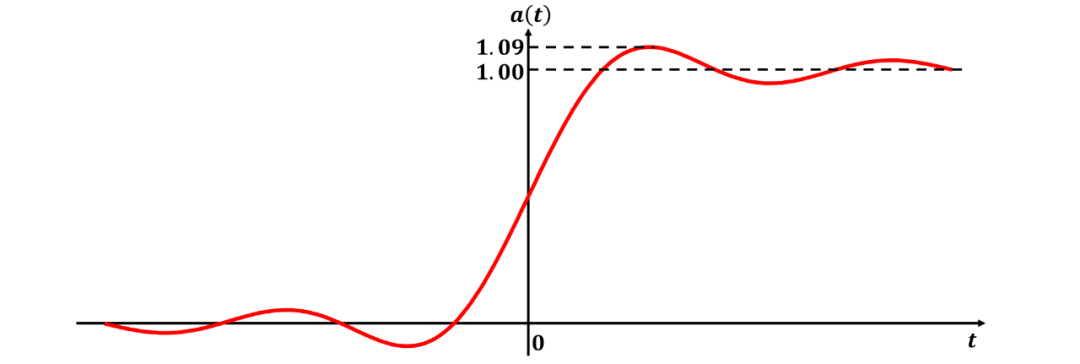
圖5 矩形濾波器的階躍響應(yīng)
它有 9% 的過(guò)沖和 0.445 的 (帶寬上升時(shí)間) 乘積。因此,雖然這樣的濾波器具有比高斯濾波器更陡峭的截止頻響,但它不是瞬態(tài)的理想濾波器。此外,矩形響應(yīng)特性比高斯響應(yīng)特性更難逼近。通過(guò)巴特沃斯、切比雪夫或勒讓德多項(xiàng)式對(duì)矩形響應(yīng)特性的逼近導(dǎo)致濾波器具有比相同階數(shù)的高斯濾波器更銳的截止頻率滾降,但此類(lèi)濾波器不可避免地會(huì)產(chǎn)生明顯的過(guò)沖,這主要是由于其相位響應(yīng)特性的非線(xiàn)性所導(dǎo)致的。
與濾波器的瞬態(tài)響應(yīng)密切相關(guān)的一個(gè)問(wèn)題是濾波器對(duì)變頻率信號(hào)的響應(yīng)。對(duì)于頻率隨時(shí)間線(xiàn)性變化的信號(hào),在其性能明顯改變之前,高斯濾波器的掃描速度大約是矩形濾波器掃描速度的八倍。高斯濾波器不會(huì)顯著的改變其性能的條件是,其中是以為單位的掃描速率,是以為單位的濾波器帶寬。(譯注:在頻譜分析儀中,其中的中頻濾波器就是高斯響應(yīng)濾波器,其中RBW就是在調(diào)整濾波器的帶寬)
IV. 相位響應(yīng)
我們必須在這里區(qū)分“理論”高斯濾波器和通過(guò)物理器件獲得的“可實(shí)現(xiàn)”的高斯濾波器。理論上的低通高斯濾波器是其頻響由式(1)給出的濾波器,將其重寫(xiě)為
即,理論上的低通高斯濾波器對(duì)所有頻率都具有零相移。由于我們通常不能同時(shí)規(guī)定物理上可實(shí)現(xiàn)的傳遞函數(shù)的相位和幅度,我們最多可以讓
并檢查相位函數(shù)是否存在使得
能在物理上實(shí)現(xiàn)。
可以證明,式(13)的幅度響應(yīng)函數(shù)不可能附加相位函數(shù),因?yàn)槭?13)不滿(mǎn)足佩利-維納準(zhǔn)則(Paley-Wiener criterion):
圖1和圖3也顯示了為什么不存在這樣的相函數(shù)。注意到,高斯濾波器對(duì)在處所施加的脈沖或階躍函數(shù)的時(shí)間響應(yīng)從開(kāi)始。顯然,物理網(wǎng)絡(luò)不是預(yù)測(cè)器,即在施加激勵(lì)之前它可能沒(méi)有任何響應(yīng)。因此,如果響應(yīng)要從而不是開(kāi)始,則有必要將響應(yīng)延遲無(wú)限長(zhǎng)的時(shí)間。同樣的問(wèn)題出現(xiàn)在任何銳截止濾波器中,包括圖5的矩形濾波器。然而,下面將顯示高斯濾波器的相位響應(yīng)可以假定為線(xiàn)性的。
一種低通高斯濾波器的逼近方法是使用大量具有級(jí)聯(lián)放大器的低通 RC 網(wǎng)絡(luò)。這樣一系列相同級(jí)的相位函數(shù) (濾波器的-截止點(diǎn)為其) 是
其中是表示級(jí)數(shù)的整數(shù)。對(duì)于
式(16)變?yōu)?/p>
即相位響應(yīng)是線(xiàn)性的,斜率為。當(dāng)時(shí),幅度響應(yīng)接近高斯函數(shù)式(13),相位響應(yīng)接近完美線(xiàn)性和無(wú)限的斜率值。
當(dāng)使用伯德圖時(shí),會(huì)得到類(lèi)似的結(jié)果。任何頻率的相角由給出,即
其中是以奈培(neper)為單位相對(duì)應(yīng)于的衰減。
其中
因此有:
這是無(wú)法實(shí)現(xiàn)的。通過(guò)集總物理元件構(gòu)建的任何濾波器的頻率響應(yīng)可以表示為以為變量多項(xiàng)式的比率。
在極高頻率下,只有具有最大指數(shù)的項(xiàng)才有效,即,對(duì)于極高頻率,幅度響應(yīng)由下式給出
其中是高頻極限下有效元件的數(shù)量。
通過(guò)集總物理元件實(shí)現(xiàn)的高斯濾波器的幅度響應(yīng),無(wú)論怎么逼近,都將在高頻極限由式(21)而不是式(19)給出。現(xiàn)在假設(shè)一個(gè)可實(shí)現(xiàn)的低通高斯濾波器的幅度響應(yīng)由式(19)給出,直到頻率,該頻率遠(yuǎn)高于任何感興趣的頻率,并且對(duì)于所有超過(guò)的頻率,由式(21)給出。忽略過(guò)渡區(qū)域,則式(18)可以寫(xiě)成
因此,隨著濾波器逼近于高斯濾波器的區(qū)域增加,相位響應(yīng)線(xiàn)性區(qū)域及其斜率也增加。
線(xiàn)性相位響應(yīng)是我們所希望的,因?yàn)閷?duì)于給定的幅度響應(yīng)特性,它會(huì)產(chǎn)生最小的瞬態(tài)失真,因?yàn)榫€(xiàn)性相位響應(yīng)意味著每個(gè)頻率分量的時(shí)間延遲都相等。一般而言,期望相位響應(yīng)線(xiàn)性度最好延伸超過(guò)幅度響應(yīng)曲線(xiàn)下面積的 90% 以上,這對(duì)于高斯曲線(xiàn)來(lái)說(shuō)大約是12dB的范圍。
圖6顯示了測(cè)試的濾波器的相位響應(yīng),其中也顯示了幅度響應(yīng)。可以看出,線(xiàn)性相位延伸到了重要的低衰減區(qū)域以外。該濾波器的脈沖響應(yīng)和階躍響應(yīng)的波形如圖2和4所示。這些響應(yīng)的對(duì)稱(chēng)性證實(shí)了相位響應(yīng)線(xiàn)性度延伸到頻率響應(yīng)特性的相當(dāng)大的部分。
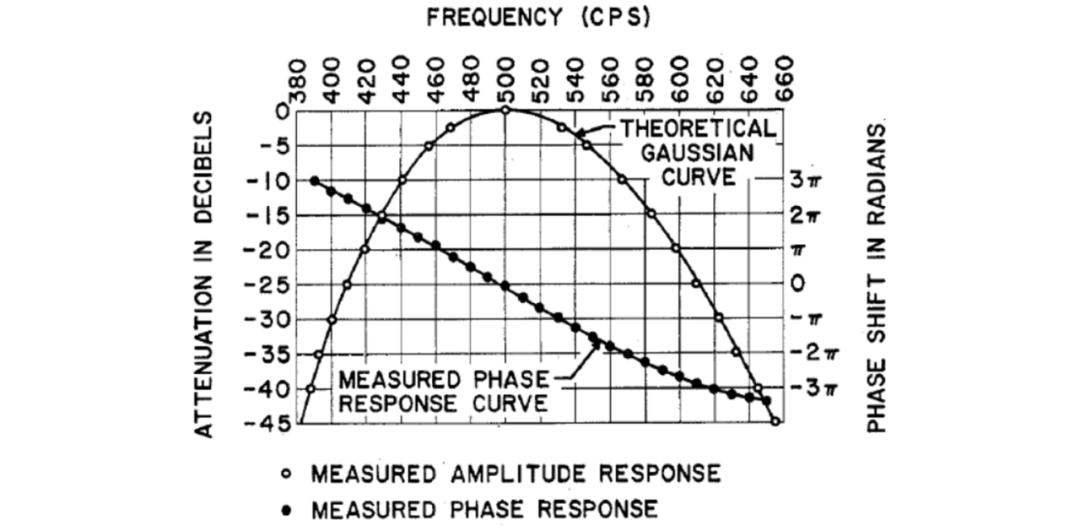
圖6 濾波器(圖8)的幅頻和相頻響應(yīng)
V. 逼近和實(shí)現(xiàn)
如第 IV 節(jié)所描述的,高斯濾波器可能僅以無(wú)限延遲為代價(jià)才能實(shí)現(xiàn),因此需要無(wú)限數(shù)量的元件。這也是其他銳截止濾波器的情況,例如矩形濾波器。然而,高斯濾波器在最重要的區(qū)域 (即低衰減頻帶) 上相對(duì)容易逼近。許多研究者建議使用一系列 RC 低通網(wǎng)絡(luò)和放大器級(jí)聯(lián)以逼近高斯形狀,但這并不代表放大器級(jí)的最有效的利用。
如果使用更有效的級(jí)間耦合網(wǎng)絡(luò),則可以用更少的級(jí)來(lái)逼近高斯濾波器。Wente提出了一種方便的方案,如圖7所示的串聯(lián)峰化(series-peaking)類(lèi)型濾波器。除其他優(yōu)點(diǎn)外,它具有簡(jiǎn)單的低通模擬電路結(jié)構(gòu)。
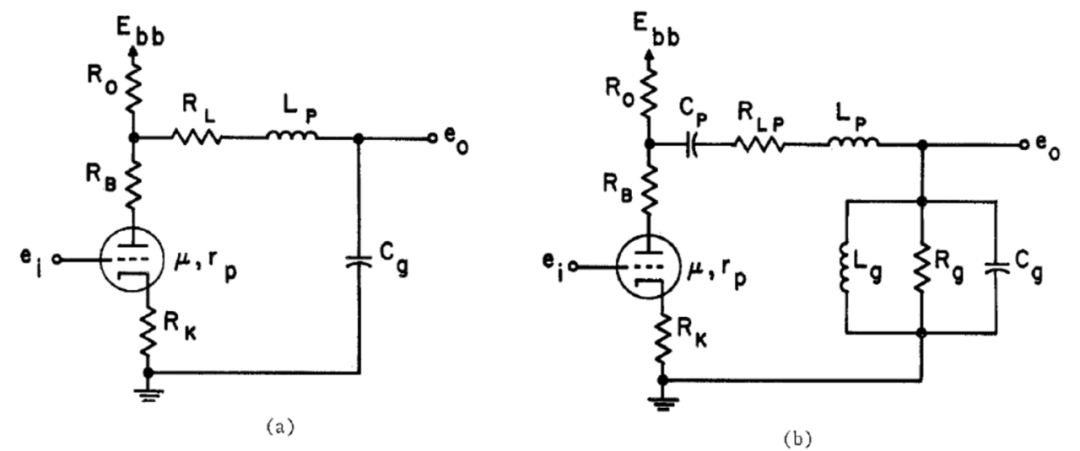
圖7 Wente提出的串聯(lián)峰化網(wǎng)絡(luò)。(a) 低通 (b) 帶通
假設(shè)需要通過(guò)5級(jí)級(jí)聯(lián)進(jìn)行逼近,然后網(wǎng)絡(luò)元件值最好通過(guò)高斯函數(shù)的冪級(jí)數(shù)展開(kāi)來(lái)獲得,如下所示:
1) 設(shè)要實(shí)現(xiàn)的高斯濾波器的幅度響應(yīng)為
其中對(duì)于低通濾波器:,對(duì)于帶通濾波器:
是與帶寬相關(guān)的常數(shù)。
2) 對(duì)高斯函數(shù)的平方冪級(jí)數(shù)展開(kāi)直到 20 次方:
是可實(shí)現(xiàn)函數(shù)。它的分母是,它的所有極點(diǎn)都在左半平面。
3) 利用以下關(guān)系找到:
代入,并僅使用平面左半部分的因子,得出
和的值可以從式(24)和式(25)中獲得。高斯函數(shù)逼近于的具體實(shí)現(xiàn),如式(26)中給出的,即,乘積通過(guò)圖7所示類(lèi)型電路的5個(gè)級(jí)聯(lián)得到5個(gè)左半平面多項(xiàng)式。
4) 通過(guò)比較式(26)的每個(gè)多項(xiàng)式因子與圖7網(wǎng)絡(luò)的傳輸方程,從而獲得每個(gè)級(jí)間網(wǎng)絡(luò)的元件值。
從式(25)可以得到,第1-3級(jí)具有單調(diào)下降的幅頻響應(yīng),而第4和5級(jí)具有雙峰幅頻響應(yīng)。附錄II給出了5級(jí)帶通逼近高斯濾波器的設(shè)計(jì)方程。(該濾波器的原理圖如圖8所示,其測(cè)得的頻率和相位響應(yīng)如圖6所示)。上述冪級(jí)數(shù)逼近如圖9的曲線(xiàn)(d)所示。曲線(xiàn)(a)是理論的高斯曲線(xiàn)。曲線(xiàn)(b)是歸因于湯姆遜(Thomson),他的逼近基于最大平坦時(shí)間延遲響應(yīng)。曲線(xiàn)(c)歸因于Wente,他使用了圖7(a)中所示的5個(gè)電路級(jí)聯(lián),每個(gè)級(jí)的值為。冪級(jí)數(shù)展開(kāi)給出了對(duì)高斯形狀的最佳逼近,如圖9所示。
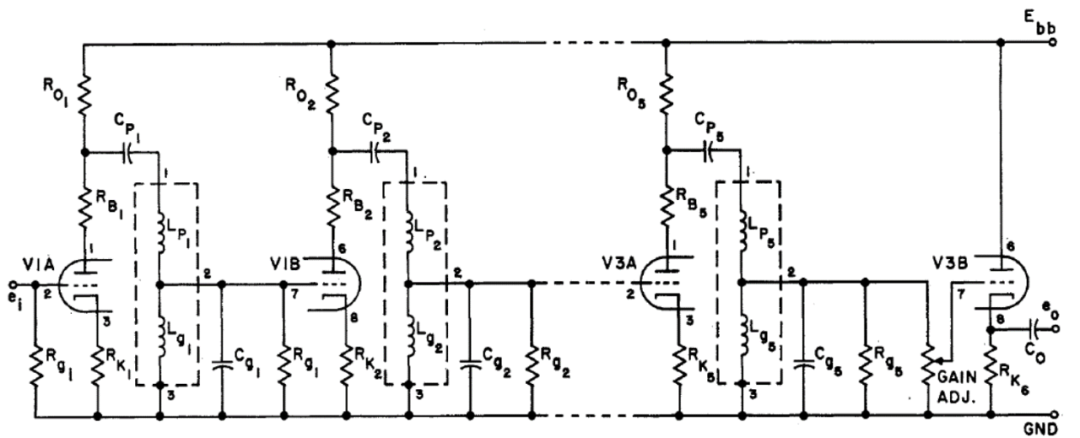
圖8 高斯帶通濾波器的5級(jí)逼近電路圖
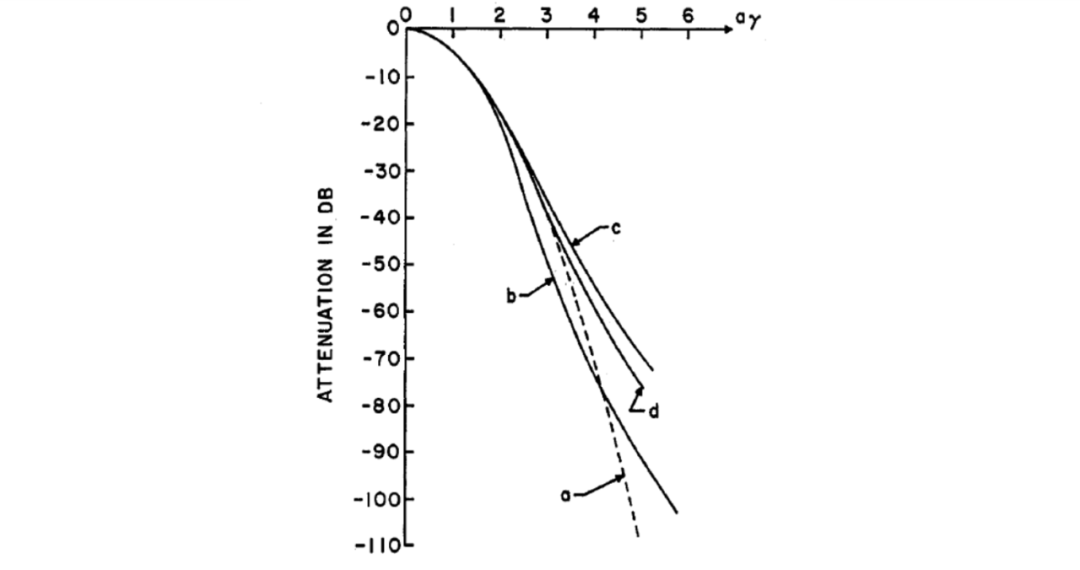
圖9 高斯響應(yīng)逼近: (a) 理想高斯濾波器曲線(xiàn) (b) 湯姆遜逼近 (c) Wente逼近 (d) 冪級(jí)數(shù)逼近
VI. 結(jié)論
已經(jīng)表明,高斯濾波器具有優(yōu)異的瞬態(tài)特性,這可以從其脈沖和階躍響應(yīng)以及其對(duì)可變頻率信號(hào)的響應(yīng)中得到證明。它還具有線(xiàn)性相位響應(yīng)、相當(dāng)尖銳的幅頻截止響應(yīng),并且相對(duì)容易逼近,這一點(diǎn)可以從5個(gè)級(jí)間耦合網(wǎng)絡(luò)的逼近值降到約45dB的事實(shí)中得到證明。
附錄 I
高斯濾波器的 (帶寬上升時(shí)間) 乘積
低通高斯濾波器頻率響應(yīng)由下式給出
根據(jù)3dB帶寬求解,可以得到:
對(duì)于低通高斯濾波器,單位階躍響應(yīng)由式(11)給出
此函數(shù)以如下形式列出
如果我們令,我們得到與式(28)相同形式的式(11),即
以表示的 (0.1 到 0.9) 上升時(shí)間為 2.6,并且
然后 (帶寬上升時(shí)間) 乘積
附錄 II
帶通濾波器逼近的設(shè)計(jì)公式
逼近值由式(26)給出
是根據(jù)的獲得的,如下所示:從式(23)
其中是帶通濾波器的中心頻率,是3dB帶寬。
式(26)現(xiàn)在可以寫(xiě)成以下形式
和的值作為(電路級(jí)編號(hào)) 的函數(shù)是從式(24)、(25)和(32)中獲得的,如下表所示:
| Stage Number | ||
|---|---|---|
| 1 | 0.1904 | 1.1527 |
| 2 | 0.1817 | 1.2395 |
| 3 | 0.1647 | 1.4497 |
| 4 | 0.1395 | 1.9059 |
| 5 | 0.1057 | 3.1221 |
圖7(b)電路網(wǎng)絡(luò)的等效電路如圖10所示
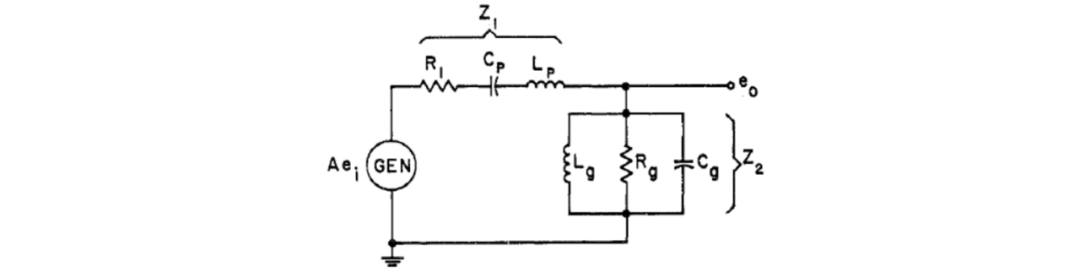
圖10 圖7(b)電路網(wǎng)絡(luò)的等效電路圖
經(jīng)過(guò)以下變換后:
圖10網(wǎng)絡(luò)的傳遞函數(shù)由下式給出
其中和和與通常定義的一樣,分別指的是和(圖10) 。
現(xiàn)令式(33)和式(36)的系數(shù)相等,即
如果圖7所示管子的參數(shù)是電子管在陽(yáng)極電流時(shí)的參數(shù),則每級(jí)在的增益取為,并且同時(shí)聯(lián)立以上方程,需要的設(shè)計(jì)方程為:
其中
其中是在的值。
和已給出。我們現(xiàn)在有 9 個(gè)未知數(shù):和和以便包含和的調(diào)諧電路在處諧振。在剩下的 7 個(gè)未知數(shù)中,3 個(gè)可以由設(shè)計(jì)者選擇,另外 4 個(gè)從式(38)到式(42)獲得。
建議選擇和而不是其他變量。和是最昂貴的元件,而是對(duì)每級(jí)增益至關(guān)重要的元件。例如,在整個(gè)濾波器 (或整個(gè)濾波器組,如在頻譜分析儀中) 中選擇相同的和是可能的,也是可取的。通常,每個(gè)級(jí)所需的和會(huì)有所不同,但這些可以很容易地通過(guò)額外串聯(lián)或并聯(lián)的電阻來(lái)進(jìn)行調(diào)整。
審核編輯:湯梓紅
-
濾波器
+關(guān)注
關(guān)注
160文章
7749瀏覽量
177737 -
帶通濾波器
+關(guān)注
關(guān)注
18文章
228瀏覽量
43095 -
階躍響應(yīng)
+關(guān)注
關(guān)注
0文章
7瀏覽量
8689 -
輸入信號(hào)
+關(guān)注
關(guān)注
0文章
447瀏覽量
12542 -
高斯濾波器
+關(guān)注
關(guān)注
0文章
9瀏覽量
1733
原文標(biāo)題:關(guān)于高斯濾波器的響應(yīng)和逼近(On the Response and Approximation of Gaussian Filter)
文章出處:【微信號(hào):電路設(shè)計(jì)小工具,微信公眾號(hào):電路設(shè)計(jì)小工具】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
高斯濾波和雙邊濾波的區(qū)別
高斯濾波的卷積核怎么確定
高斯濾波的基本原理有哪些
切比雪夫濾波器的設(shè)計(jì)步驟
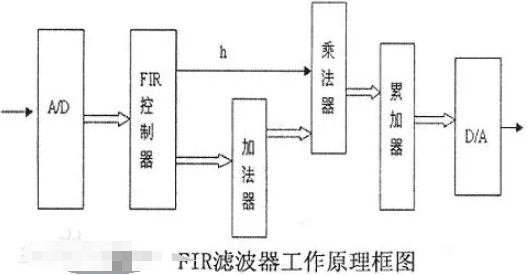
FIR濾波器的工作原理和特點(diǎn)
如何區(qū)分IIR濾波器和FIR濾波器
iir濾波器和fir濾波器的優(yōu)勢(shì)和特點(diǎn)
低通濾波器、高通濾波器、帶通濾波器的簡(jiǎn)單介紹
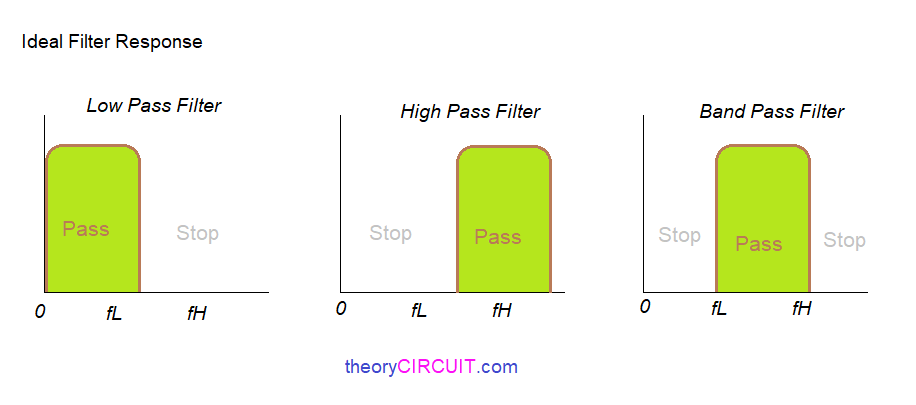
濾波器原理及其作用 濾波器電路圖分析

什么是低通濾波器?低通濾波器有什么作用?





 關(guān)于高斯濾波器的響應(yīng)和逼近
關(guān)于高斯濾波器的響應(yīng)和逼近










評(píng)論