在此我們以綠皮書中的例子為說明。
rand bit x; rand bit[1:0] y;
without order, solve before的概率分布
在此設計三種不同的隨機先后順序,分析x和y取值的其概率分布。
1. without order:
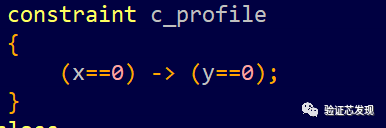
在x和y互相耦合的約束下,{x,y}的合法取值共有5種,每種取值的概率分別為1/5。
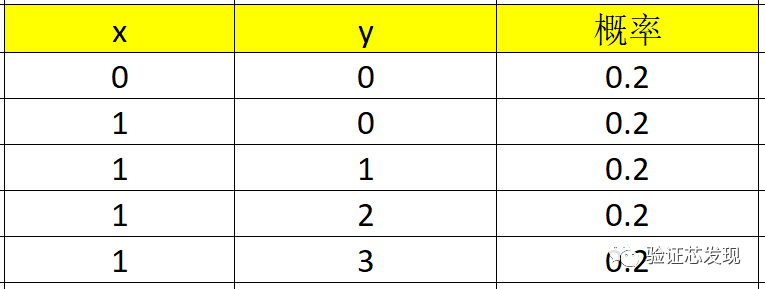
因此,x=0的取值概率為:0.2,y=0的取值概率為:0.2+0.2=0.4,y=1,2,3的取值概率都是0.2。這種分析方式也是符合SV語法手冊的說明,參見SV語法手冊第18.5.10小節的說明。
注:這種概率的分布和綠皮書中的分析并不相同,這是由于綠皮書中采用vcs仿真器不同版本的差異造成的。在較新的vcs版本中,有ntb_solver_mode仿真選項,在設置ntb_solver_mode=1時,可以得到綠皮書中的結果;ntb_solver_mode=2或者使用默認設置,得到的就是上面的分析結果。
2. solve x before y:
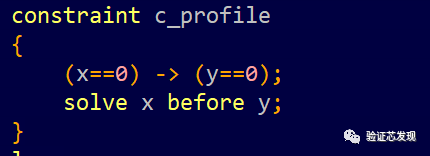
solve-before并沒有改變合法解的空間,只是改變了概率分布,由于x先于y求解,因此x的隨機不受y取值的影響,其概率分布如下:
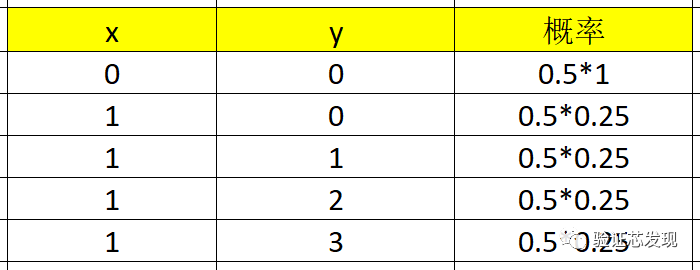
因此,x=0和1的取值概率都是0.5,y=0的取值概率為:0.5+0.125=0.625,其余取值概率都為0.125。
3. solve y before x:
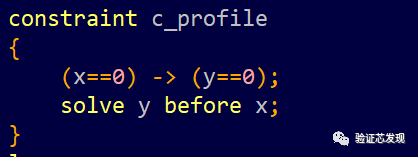
和第2點類似,概率分布如下:
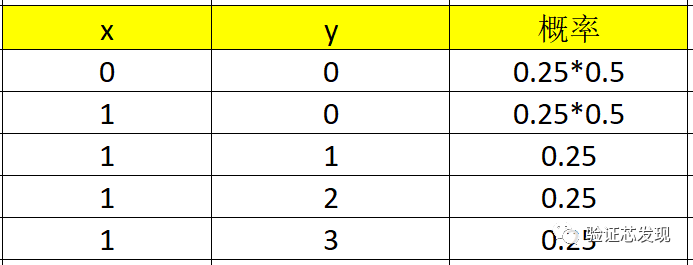
因此,y的取值是均勻分布,都是0.25,x=0的取值概率都是0.125,x=1的取值概率為:0.25*3+0.25*0.5=0.875。
上述三種約束,使用vsim仿真,提取x和y的取值概率分布如下:
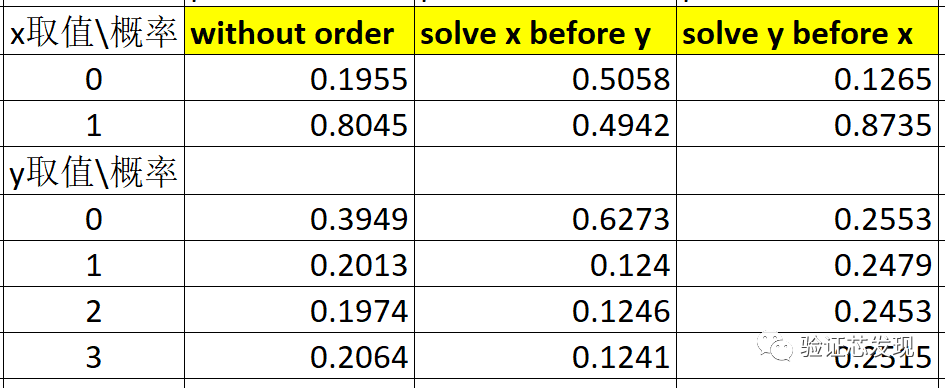
因此,無論是選擇哪一種約束順序,由于x和y之間存在耦合,二者的取值概率都不會同時滿足各自的均勻分布,即x=0/1:0.5和y=0,1,2,3:0.25不能同時出現。
進一步,如果上述的約束中,如果指定了x或者y的概率分布,結果又會如何?
指定x的概率分布:without order, solve before的差異分析
添加x的dist概率分布,分別對without order,solve_before方式進行測試。
without order:
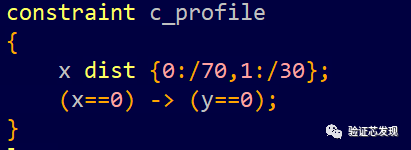
solve x before y:
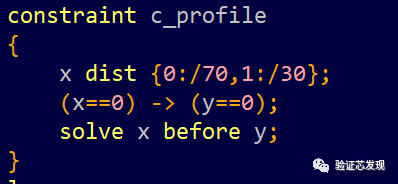
solve y before x: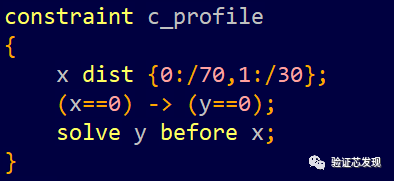
測試結果如下: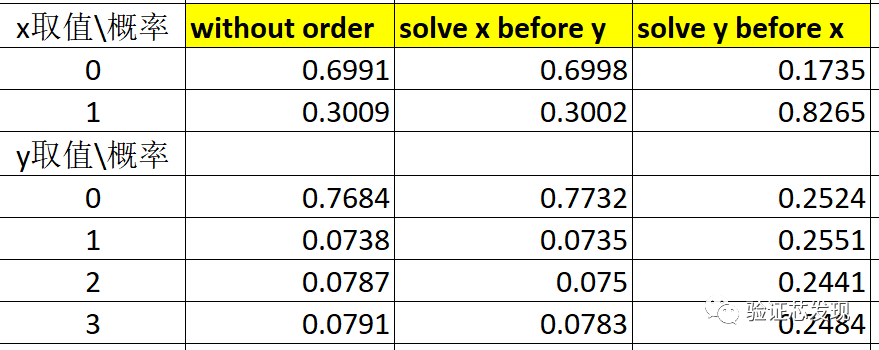
上表實測結果的理論分析值如下:
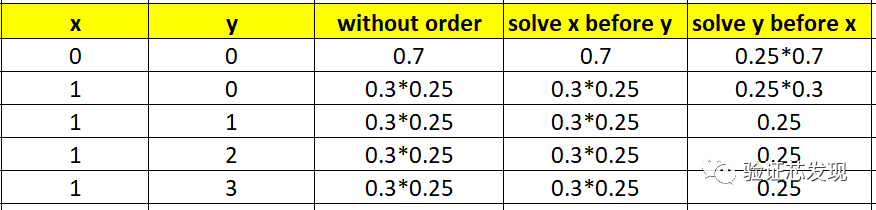
從中可以看出:
(1)在without order和solve x before y條件下,x的dist概率分布會得到滿足;
(2)在solve y before x的條件下,優先滿足solve before順序,y是均勻分布;
指定y的概率分布:without order, solve before的差異分析
添加x的dist概率分布,分別對without order,solve_before方式進行測試。
without order:
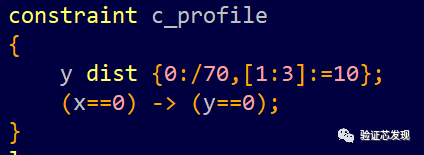
solve x before y:
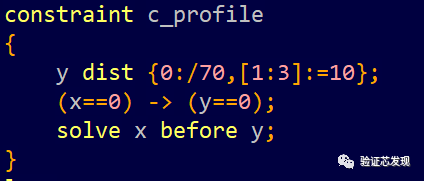
solve y before x:
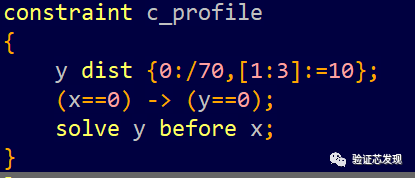
測試結果如下:
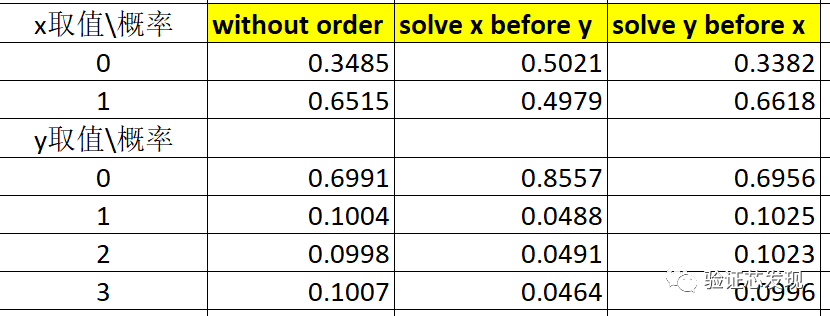
上表實測結果的理論分析值如下:
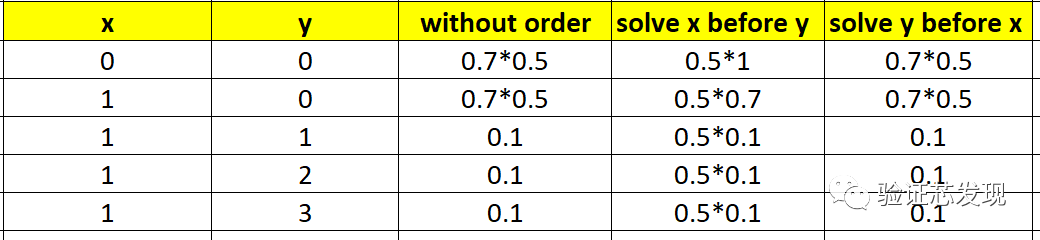
從中可以看出:
(1)在without order和solve y before x條件下,y的dist概率分布會得到滿足;
(2)在solve x before y的條件下,優先滿足solve before順序,x是均勻分布;
同時指定x和y的概率分布:without order, solve before的差異分析
添加x的dist概率分布,分別對without order,solve_before方式進行測試。
without order:
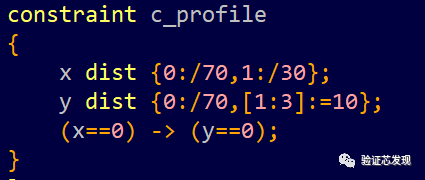
solve x before y:
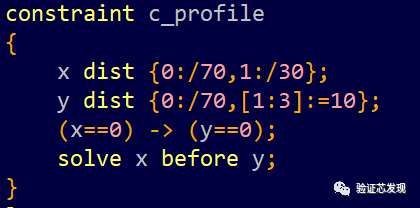
solve y before x:
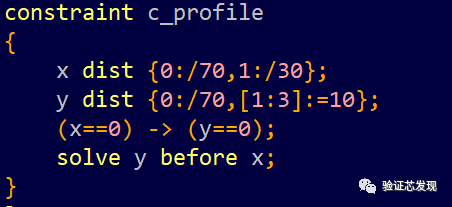
測試結果如下:
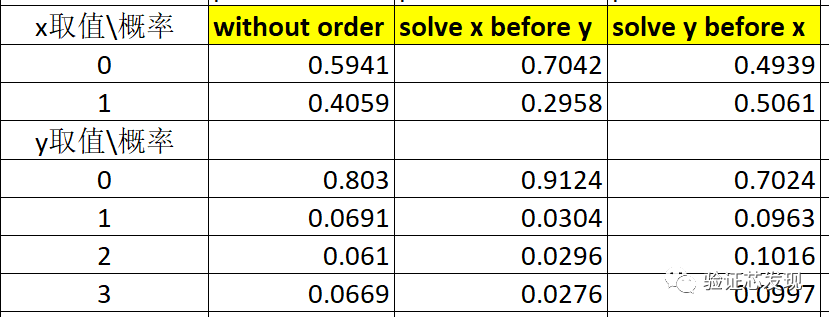
上表實測結果的理論分析值如下:
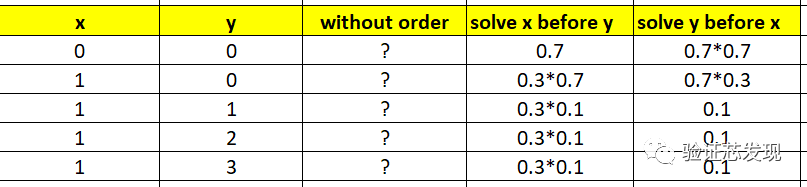
從中可以看出:
(1)solve before 仍會優先得到滿足;
(2)在同時指定dist概率分布時,without order的概率理論值分析方法暫時沒有確定,同時也沒有和測試值吻合。
總的來看,使用->或者if-else時,參數的概率分布會變得復雜且不易理解,尤其涉及到多條件蘊含時,某些參數的概率分布很難做出預期,因此更加需要后續的功能覆蓋率加以分析,找出不合理的約束。
審核編輯:劉清
-
仿真器
+關注
關注
14文章
1016瀏覽量
83644 -
Verilog
+關注
關注
28文章
1345瀏覽量
109986
原文標題:systemverilog 隨機約束implication的概率分析
文章出處:【微信號:處芯積律,微信公眾號:處芯積律】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
概率隨機數生成【子模塊】
設計驗證中的隨機約束
M序列偽隨機碼在測距回答概率控制中的應用
添加時序約束的技巧分析
基于概率隨機裁剪的圖像縮放算法




 systemverilog隨機約束implication的概率分析
systemverilog隨機約束implication的概率分析










評論