原理
卡爾曼濾波器是一種基礎預測定位算法。原理非常簡單易懂。核心過程可以用一個圖說明:
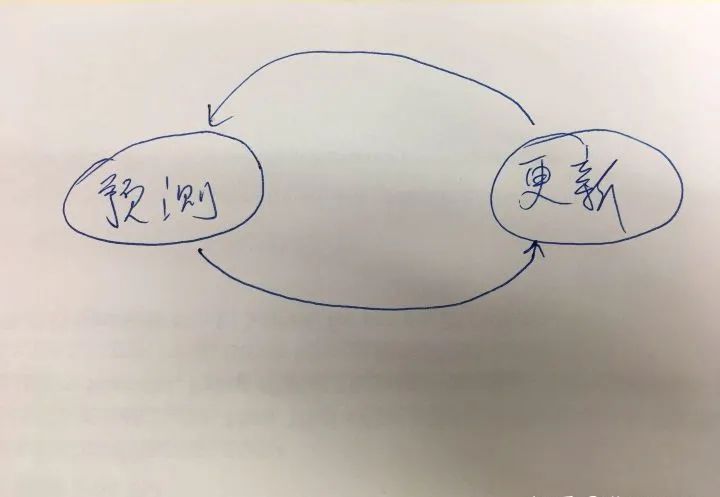
本質上就是這兩個狀態過程的迭代,來逐步的準確定位。 預測:當前狀態環境下,對下一個時間段t的位置估計計算的值。 更新:更具傳感器獲取到比較準確的位置信息后來更新當前的預測問位置,也就是糾正預測的錯誤。 你可能要問為什么有傳感器的數據了還要進行更新?因為在現實世界中傳感器是存在很多噪聲干擾的,所以也不能完全相信傳感器數據。卡爾曼算法依賴于線性計算,高斯分布,我們以一維定位來介紹算法的實現。
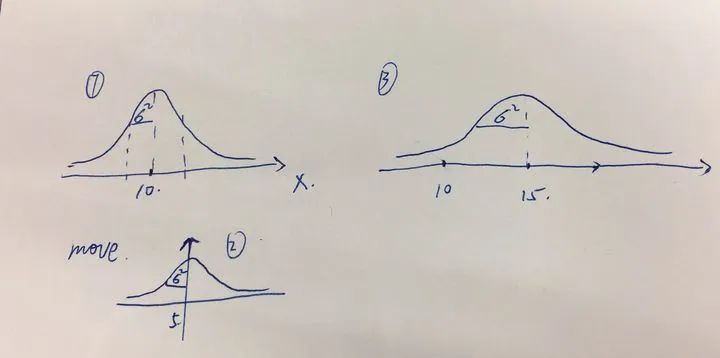

接下來我們開更新,預測后我們獲取到傳感器數據,表示目前傳感器發現小車的位置應該是在26這個位置,在這種情況下,我們肯定是覺得傳感器的準確度比我之前的預測瞎猜要來的準確。 所以方差自然會比較小,最終我們覺得真是的小車位置應該是更靠近傳感器數據的,而且方差會縮小,以至于,想想也很清楚,我猜了一個預測值,現在有個專家告訴了我相對比較靠譜的數據,那我對小車的位置的自信度肯定會上升啊。 最終小車的位置經過這個時間段t的更新就是下圖紅色的高斯圖:
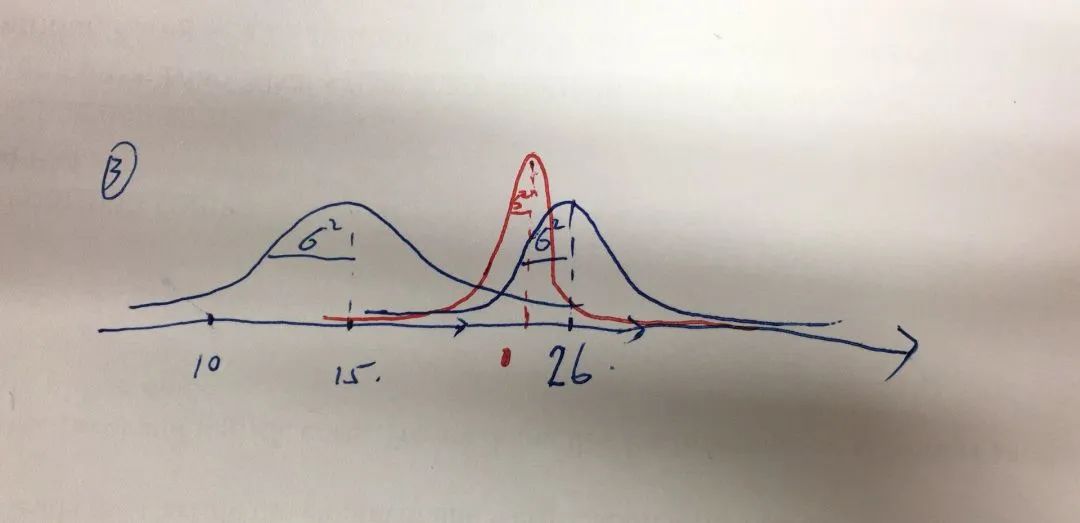
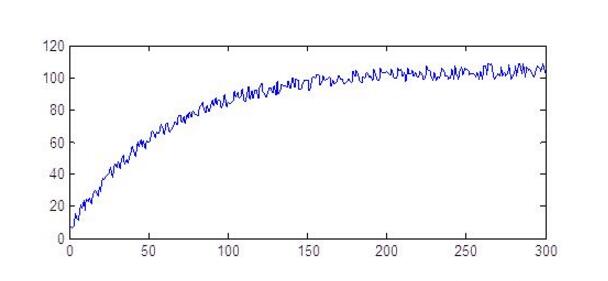
就這樣不停的移動更新,最終小車的位置就會越來越準確。
一維模型下的Kalman公式:
預測
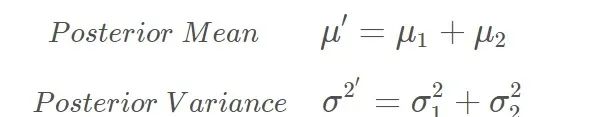
更新
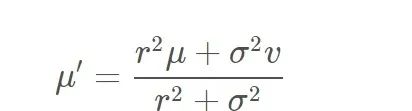
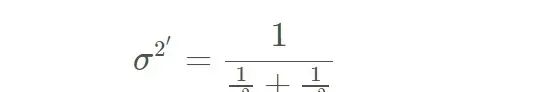
參考代碼:
using namespace std;
double new_mean, new_var;
tuple<double, double> measurement_update(double mean1, double var1, double mean2, double var2)
{
new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2);
new_var = 1 / (1 / var1 + 1 / var2);
return make_tuple(new_mean, new_var);
}
tuple<double, double> state_prediction(double mean1, double var1, double mean2, double var2)
{
new_mean = mean1 + mean2;
new_var = var1 + var2;
return make_tuple(new_mean, new_var);
}
int main()
{
//Measurements and measurement variance
double measurements[5] = { 5, 6, 7, 9, 10 };
double measurement_sig = 4;
//Motions and motion variance
double motion[5] = { 1, 1, 2, 1, 1 };
double motion_sig = 2;
//Initial state
double mu = 0;
double sig = 1000;
for (int i = 0; i < sizeof(measurements) / sizeof(measurements[0]); i++) {
tie(mu, sig) = measurement_update(mu, sig, measurements[i], measurement_sig);
printf("update: [%f, %f]
", mu, sig);
tie(mu, sig) = state_prediction(mu, sig, motion[i], motion_sig);
printf("predict: [%f, %f]
", mu, sig);
}
return 0;
}
審核編輯 :李倩
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
傳感器
+關注
關注
2548文章
50678瀏覽量
752010 -
定位算法
+關注
關注
0文章
61瀏覽量
14988 -
卡爾曼濾波器
+關注
關注
0文章
54瀏覽量
12178
發布評論請先 登錄
相關推薦




 基礎卡爾曼濾波
基礎卡爾曼濾波
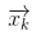
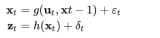










評論