前言

在日常編程中， 數值類型 （ numeric types ）是我們打交道最多的類型，可能沒有之一。除了最熟悉的 int，還有 long、float、double 等。正因太熟悉，我們往往不會深究它們的底層原理。因為平時的工作中，知道個大概，也夠用了。

但，在某些業務場景下，比如金融業務，數值運算不準確會帶來災難性的后果。這時，你就必須清楚數值類型的二進制表示、截斷、轉型等原理，否則很難保證運算結果的正確性。

另外，數值類型也是一個容易被黑客攻擊的點，考慮如下一段代碼：

// C++
/* Declaration of library function memcpy */
void *memcpy(void *dest, void *src, size_t n);
/* Kernel memory region holding user-accessible data */
#define KSIZE 1024
char kbuf[KSIZE];
/* Copy at most maxlen bytes from kernel region to user buffer */
int copy_from_kernel(void *user_dest, int maxlen) {
    /* Byte count len is minimum of buffer size and maxlen */
    int len = KSIZE < maxlen ? KSIZE : maxlen;
    memcpy(user_dest, kbuf, len);
    return len;
}

如果你熟悉數值類型的原理，一定會敏銳察覺出第 10 行存在 int 到 size_t 的類型轉換。在 64 位系統中，size_t 通常被定義為 unsigned long 類型，如果攻擊者在調用 copy_from_kernel 時，特意傳入一個負數的 maxlen，轉型到 memcpy 中的 n 將會是一個很大的正數，從而導致了內存拷貝的越界！

數值類型是計算機編程的基礎，用的很多，也很重要，理解它的底層原理，有助于寫出正確的代碼，避免一些意料之外的錯誤 。

每個計算機系統都有固定的 word size ，也即常說的 xx 位，它也是指針的大小，跟 虛擬內存 相關，比如一個 w 位系統上的應用程序，最多能夠訪問 byte 大小的虛擬內存。

最常用的是 32 位 和 64 位 系統，某些數值類型在它們之上會有些差異，比如 long 類型 在 32 位系統上是 32 bit 大小，在 64 位系統上是 64 bit 大小。 考慮如今 64 位系統逐漸成為主流，本文會以它作為基礎，進行數值類型的介紹 。

整數

在計算機系統中，整數可以分成 無符號 （ unsigned ）整數 和 有符號 （ signed ）整數 兩大類，這之下，按照類型表示的 bit 位大小，又可細分成 8 位的 char/byte/int8 、16 位的 short/innt16、32 位的 int/int32 和 64 位的 long/int64，它們的取值范圍如下：

死記這個表不容易，下面我們將試圖從二進制編碼層面去理解它。

二進制編碼

整數在計算機系統上都是以二進制存儲的，對于一個 w 位的整數 ，它的二進制表示寫成這樣：

其中， 取值 或 。

無符號編碼（Unsigned Encodings）

在二進制表示的基礎上，無符號編碼 是這樣：

比如，w = 4 場景下的一些例子：

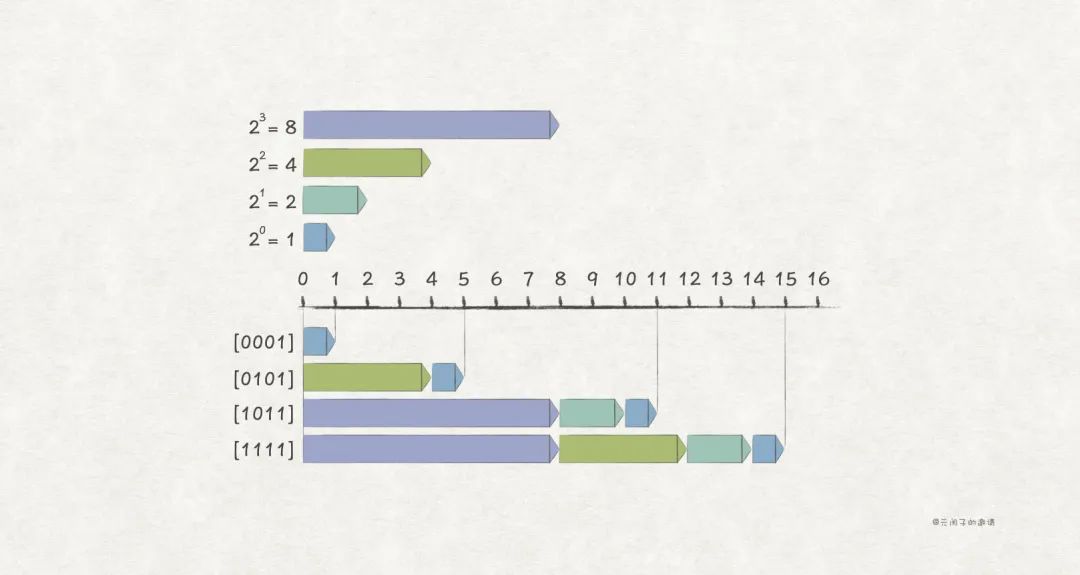
由上述可知， 無符號編碼無法表示負數，因此只能表示無符號整數 。為了表示有符號整數，還要探尋另一種編碼方式。

原碼編碼（True Form Encodings）

為了區分正數和負數，很容易想到使用一個 bit 位作為 符號位 ， 表示正數， 表示負數。在無符號編碼的基礎上，使用最高位作為符號位，其他位含義不變，得出 原碼編碼 形式：

比如，w = 4 場景下的一些例子：

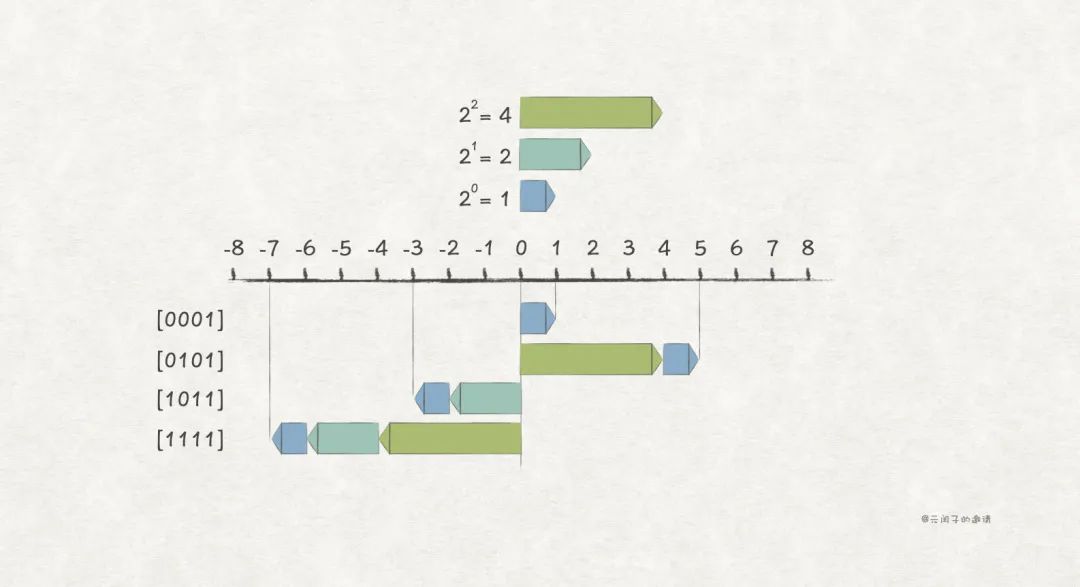
雖然原碼編碼方式簡單直觀，但它還存在兩個問題：

（1） 存在兩種編碼形式

原碼編碼方式下， 存在兩種編碼形式， 和 。同一個整數值，卻有兩種編碼，這對計算機系統來說沒什么意義，反而是一種浪費。

（2）帶負數的加法運算不正確

原碼編碼方式下，兩個正數的加法沒問題，一旦帶上負數，結果就出錯了：

所以，原碼編碼方式，注定不會被使用。

補碼編碼（Two's-complement Encodings）

于是，補碼編碼 被發明，它也是建立在無符號編碼的基礎上，仍然取最高位為符號位，編碼方式是這樣：

它與無符號編碼的唯一區別是，最高位的取值從 變成了 。

比如，w = 4 場景下的一些例子：

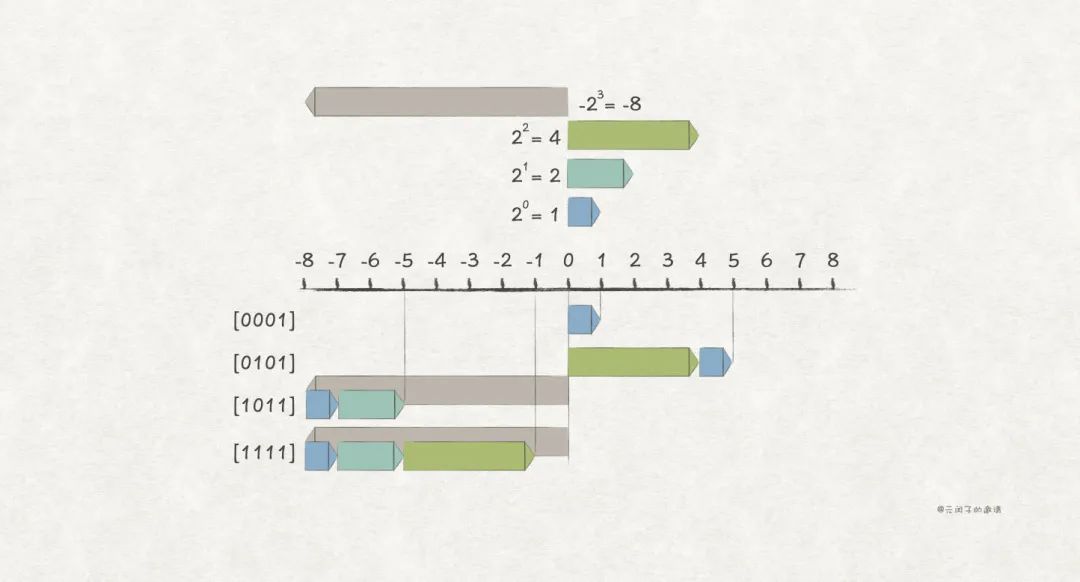
補碼編碼很巧妙地解決了原碼編碼的兩個問題：

首先，0 在補碼編碼下只有一種編碼形式， 。

此外，帶負數的加法運算，也正確了。

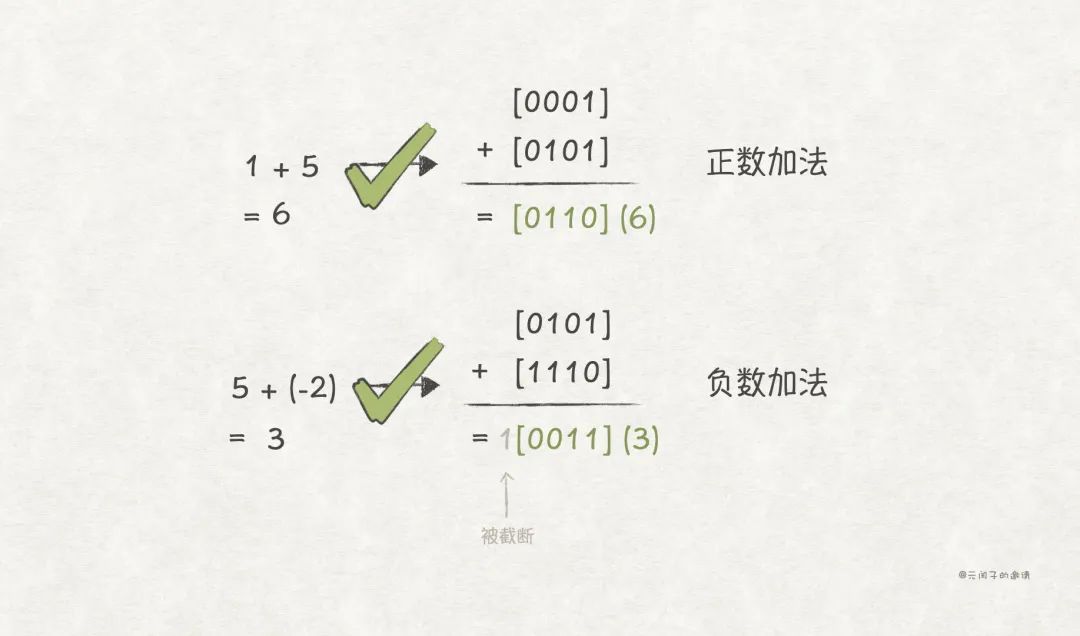
因為補碼編碼的簡單和正確性，目前，幾乎所有的計算機系統，都采用補碼編碼來表示有符號整數 。

位運算

位運算主要包含 取反 、 與 、 或 、 異或 、移位 等幾種，我們在業務開發時用得比較少，但如果你有閱讀開源代碼的習慣，就會經常發現它們的蹤跡。如果碰巧對位運算不熟悉，那么閱讀這些代碼，就同讀天書一般。

取反（~）、與（&）、或（|）、異或（^）的規則比較簡單：

移位運算，可以分成 左移 和 右移 兩種，其中，右移又可分為 邏輯右移 和 算術右移 。

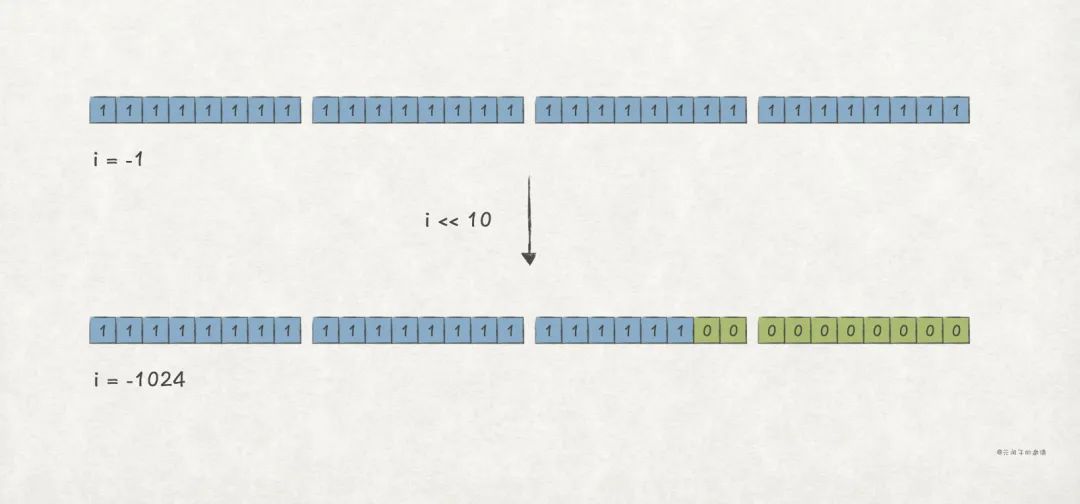
左移（<<）運算，是對二進制整數，向左移若干位，高位丟棄，低位補零 。也即，對 左移 位，得到 。

比如，對 int i = -1 左移 10 位，會得到 i = -1024 的結果：

// Java語言
public static void main(String[] args) {
    int i = -1;
    System.out.println("Before << , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
    i <<= 10;
    System.out.println("After << , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
}
// 輸出結果：
Before << , i's value is -1
i's binary string is 11111111111111111111111111111111
After << , i's value is -1024
i's binary string is 11111111111111111111110000000000

在 C/C++ 中，兩種右移操作符都是 >>，對無符號整數用的是邏輯右移，對有符號整數用的是算術右移；在 Java 中，邏輯右移的操作符是 >>>，算術右移的操作符是 >>。為了方便區分，下文統一用 Java 的表示方法。

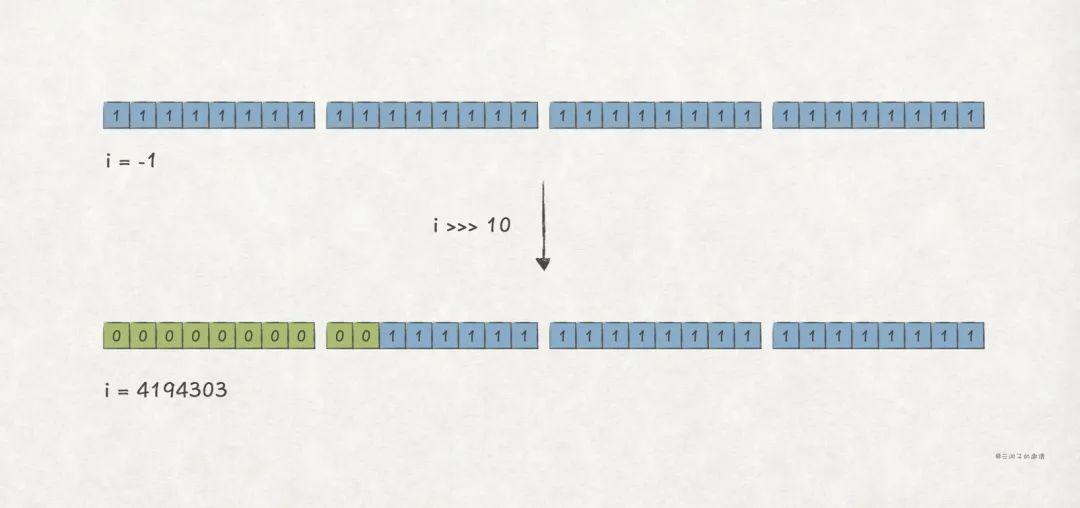
邏輯右移（>>>）運算，是對二進制整數，向右移若干位，高位補零，低位丟棄 。也即，對 邏輯左移 k 位，得到 。

比如，對 int i = -1 邏輯右移 10 位，會得到 i = 4194303 的結果：

// Java語言
public static void main(String[] args) {
    int i = -1;
    System.out.println("Before >>> , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
    i >>>= 10;
    System.out.println("After >>> , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
}
// 輸出結果：
Before >>> , i's value is -1
i's binary string is 11111111111111111111111111111111
After >>> , i's value is 4194303
i's binary string is 1111111111111111111111

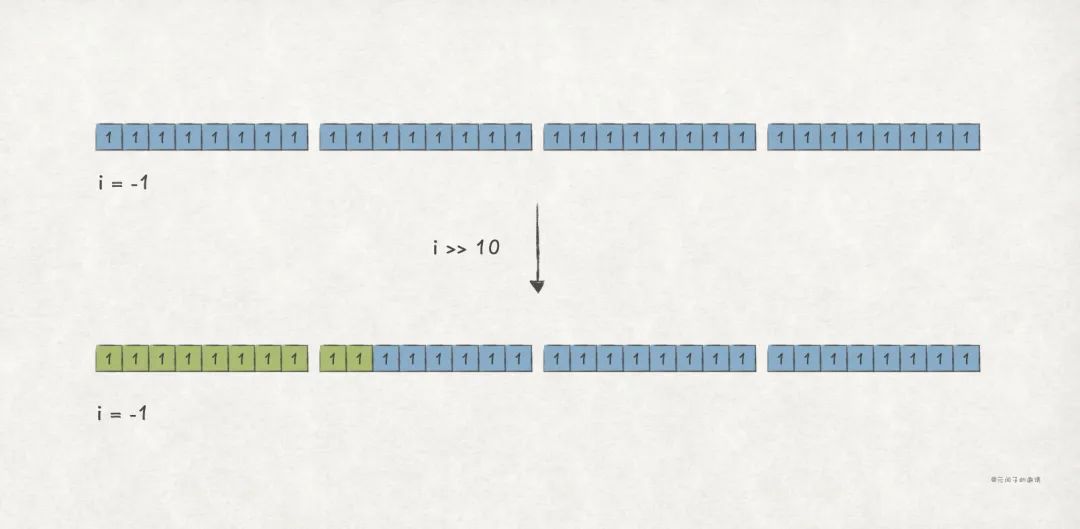
算術右移（>>）運算，是對二進制整數，向右移若干位，高位補符號位，低位丟棄 。也即，對 邏輯左移 k 位，得到 。

比如，對 int i = -1 算術右移 10 位，仍會得到 i = -1 的結果：

// Java語言
public static void main(String[] args) {
    int i = -1;
    System.out.println("Before >> , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
    i >>= 10;
    System.out.println("After >> , i's value is " + i);
    System.out.println("i's binary string is " + Integer.toBinaryString(i));
}
// 輸出結果：
Before >> , i's value is -1
i's binary string is 11111111111111111111111111111111
After >> , i's value is -1
i's binary string is 11111111111111111111111111111111

目前為止，介紹移位運算的原理時，我們都默認 k < w，如果 k >= w 會怎樣 ？

比如， 左移 w 位，結果會是 嗎：

// Java語言
public static void main(String[] args) {
    int i1 = -1;
    System.out.println("Before << 31, i1's value is " + i1);
    System.out.println("i1's binary string is " + Integer.toBinaryString(i1));
    i1 <<= 31;
    System.out.println("After << 31, i1's value is " + i1);
    System.out.println("i1's binary string is " + Integer.toBinaryString(i1));

    int i2 = -1;
    System.out.println("Before << 32, i2's value is " + i2);
    System.out.println("i2's binary string is " + Integer.toBinaryString(i2));
    i2 <<= 32;
    System.out.println("After << 32, i2's value is " + i2);
    System.out.println("i2's binary string is " + Integer.toBinaryString(i2));
}
// 輸出結果：
Before << 31, i1's value is -1
i1's binary string is 11111111111111111111111111111111
After << 31, i1's value is -2147483648
i1's binary string is 10000000000000000000000000000000
Before << 32, i2's value is -1
i2's binary string is 11111111111111111111111111111111
After << 32, i2's value is -1
i2's binary string is 11111111111111111111111111111111

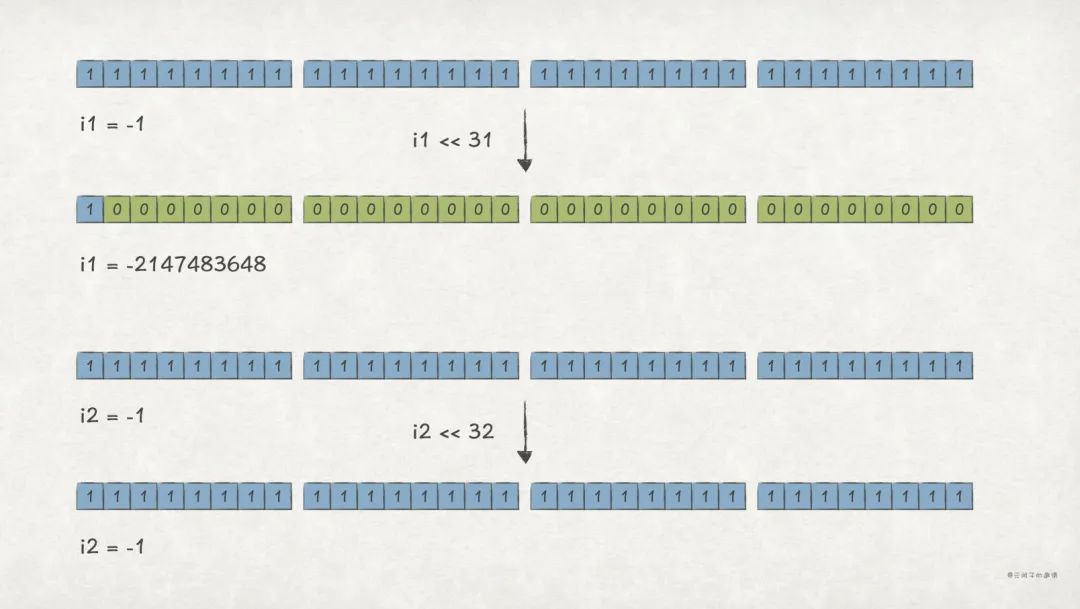
上述例子中， w = 32，我們發現 k = 31 時，結果還符合預期；當 k = 32 時，結果不是 0，而是 -1，也即相當于 k = 0 時的結果。

原因是這樣，對 w 位整數 x，當執行 x << k 時，實際執行的是 x << (k % w)。所以，當 i2 << 32 時，實際是 i2 << 32 % 32 = i2 << 0。

右移操作也遵循同樣的規則，也即 x >> k = x >> (k % w)， x >>> k = x >>> (k % w)。