根據,在線性可分情況下,支持向量機尋找最優分類超平面的優化問題可以表示為:
最小化:1/2||ω||2,
限制條件:yi(ωTXi+b)≥1,i=1~N。
求解上述最優化問題,可得出一組ω和b的值,使得ωTx+b=0所表示的超平面為最優分類超平面。
但在訓練樣本是線性不可分的情況下,上述最優化問題不存在合適的解(個人理解:不存在合適的解的原因是上述最優化問題的本質是求解最優分類超平面,最優分類超平面應滿足可將訓練數據完全分為兩類的條件,但在訓練樣本是線性不可分的情況,不存在滿足上述條件的超平面)。
因此,尋找線性不可分的訓練樣本的最優超平面時,需將上述優化問題的限制條件放松。放松限制條件的方式是引入松弛變量δi(slack variable),將上述優化問題的限制條件改寫為:
yi(ωTXi+b)≥1-δi,i=1~N
在線性不可分的情況下,訓練樣本的數據無法滿足均yi(ωTXi+b)≥1,但可通過調整δi的值使所有訓練數據均滿足yi(ωTXi+b)≥1-δi。同時,為使分類的準確性盡可能高,δi的值也需被限定。
根據上述思路,在線性不可分的情況下,支持向量機尋找最優分類超平面的優化問題可以表示為:
最小化:1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2,
限制條件:(1)δi≥0,i=1~N;(2)yi(ωTXi+b)≥1-δi,i=1~N。
其中,最小化1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2使δi的取值盡可能小,C為比例因子,C的值需人為設定。算法中需人為設定的參數被稱為算法的超參數(hyper parameter)。
在實際應用中,開發人員會不斷被變化超參數值,并測試各種超參數算法的識別率,以選取使算法識別率達至最高的超參數值。
如果一個算法的超參數越多,該算法需手動調整的部分越多,其自動性越低,支持向量機是超參數較少的算法模型,超參數較多的算法模型包括:人工神經網絡、卷積神經網絡(根據百度百科:卷積神經網絡是深度學習的代表算法之一)等。
盡管在線性不可分的情況下,機器學習可以通過使1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2最小化尋找最優分類超平面,但該方法的分類準確率不一定較高。
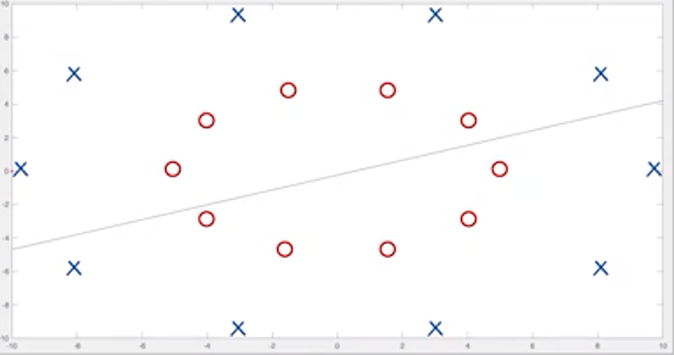
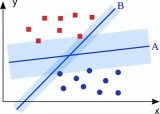
如圖一所示,圖一中的直線為機器學習通過支持向量機尋找最優分類超平面,但該直線對圖一中圓圈和叉的分類的準確率與隨機猜測的準確率差異不大。
 ?
?
圖一,圖片來源:中國慕課大學《機器學習概論》
此情況出現的原因是通過使1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2最小化尋找最優分類超平面的算法模型是線性的,即假設算法模型的分類函數是線性的。因此,該算法模型對分類函數為非線性函數的訓練樣本進行分類時,將出現分類錯誤的情況。
當訓練樣本的非線性分類函數與線性函數差異較大時,分類錯誤的情況出現的概率將較大,可能出現分類的準確率與隨機猜測的準確率差異不大的情況。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20850 -
機器學習
+關注
關注
66文章
8377瀏覽量
132409 -
卷積神經網絡
+關注
關注
4文章
366瀏覽量
11851
原文標題:機器學習相關介紹(9)——支持向量機(線性不可分情況)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何優化單片機項目的功耗
25G/28G重定時器與轉接驅動器在常見應用中的最優化實現

量子計算場景實用秘籍:開物SDK之“高階函數降階”
基于計算機視覺與機器學習技術的跌倒風險預測

寬帶熱成像中超平面光學元件的應用研究
COMSOL Multiphysics在超材料與超表面仿真中的應用
什么是中斷向量偏移,為什么要做中斷向量偏移?




 支持向量機尋找最優分類超平面的優化問題
支持向量機尋找最優分類超平面的優化問題











評論