奈奎斯特采樣定理，或更準(zhǔn)確地說(shuō)是奈奎斯特-香農(nóng)定理，是支配混合信號(hào)電子系統(tǒng)設(shè)計(jì)的基本理論原則。

如果沒(méi)有模數(shù)轉(zhuǎn)換和數(shù)模轉(zhuǎn)換，就不會(huì)存在我們所知道的現(xiàn)代技術(shù)。事實(shí)上，這些操作已經(jīng)變得如此普遍，以至于說(shuō)模擬信號(hào)可以轉(zhuǎn)換為數(shù)字信號(hào)再轉(zhuǎn)換回模擬信號(hào)而不會(huì)丟失任何重大信息，這聽(tīng)起來(lái)像是不言而喻。

但是我們?cè)趺粗来_實(shí)是這樣呢？為什么采樣是一種非破壞性操作，當(dāng)它似乎丟棄了我們?cè)诟鱾€(gè)樣本之間觀察到的如此多的信號(hào)行為時(shí)？

我們究竟如何從一個(gè)看起來(lái)像這樣的信號(hào)開(kāi)始：

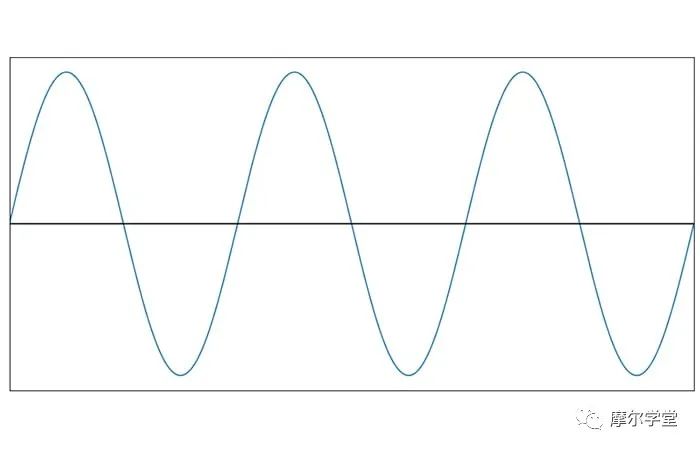
并將其數(shù)字化為：

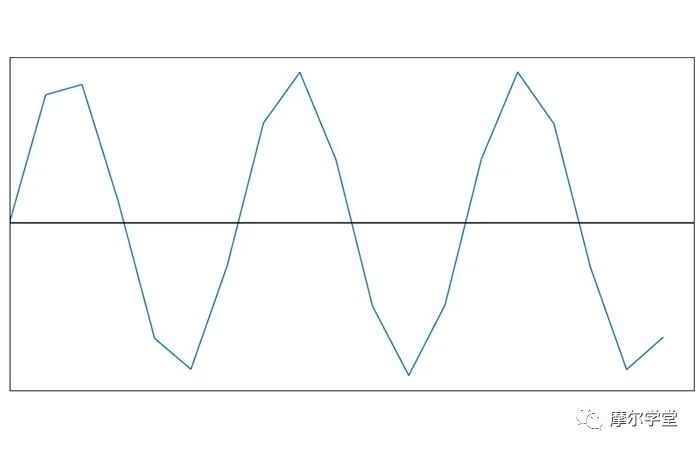
然后還敢聲稱(chēng)可以在不丟失信息的情況下恢復(fù)原始信號(hào)？

奈奎斯特-香農(nóng)定理

這樣的說(shuō)法是可能的，因?yàn)樗犀F(xiàn)代電氣工程最重要的原則之一：

如果系統(tǒng)以超過(guò)信號(hào)最高頻率至少兩倍的速率對(duì)模擬信號(hào)進(jìn)行均勻采樣，則可以從采樣產(chǎn)生的離散值中完美地恢復(fù)原始模擬信號(hào)。

關(guān)于這個(gè)定理還有很多要說(shuō)的，但首先，讓我們?cè)囍宄绾畏Q(chēng)呼它。

香農(nóng)？奈奎斯特？科捷利尼科夫？惠特克？

我當(dāng)然不是決定誰(shuí)應(yīng)該因制定、證明或解釋香農(nóng)-奈奎斯特-科特尼科夫-惠特克采樣和插值理論而獲得最多榮譽(yù)的人。所有這四個(gè)人都有某種顯著的參與。

然而，Harry Nyquist 的角色似乎已經(jīng)超出了其原有的意義。例如，在Tan 和 Jiang 的Digital Signal Processing: Fundamentals and Applications中，上述原理被確定為“Shannon sampling theorem”，在Sedra 和 Smith 的Microelectronic Circuits中，我發(fā)現(xiàn)以下句子：“The fact that we可以對(duì)有限數(shù)量的樣本進(jìn)行處理……而忽略樣本之間的模擬信號(hào)細(xì)節(jié)是基于……香農(nóng)的采樣定理。”

因此，我們可能應(yīng)該避免使用“奈奎斯特采樣定理”或“奈奎斯特采樣理論”。如果我們需要將一個(gè)名稱(chēng)與這個(gè)概念相關(guān)聯(lián)，我建議我們只包括 Shannon 或包括 Nyquist 和 Shannon。事實(shí)上，也許是時(shí)候過(guò)渡到更匿名的東西了，比如“基本采樣定理”。

如果您覺(jué)得這有點(diǎn)迷惑，請(qǐng)記住，上述采樣定理與奈奎斯特速率不同，后者將在本文后面進(jìn)行解釋。我認(rèn)為沒(méi)有人試圖將奈奎斯特與其速率分開(kāi)，所以我們最終得到了一個(gè)很好的折衷方案：香農(nóng)得到定理，奈奎斯特得到速率。

時(shí)域采樣理論

如果我們將采樣定理應(yīng)用于頻率為 f SIGNAL的正弦波，如果我們想要實(shí)現(xiàn)完美重建，就必須在 f SAMPLE ≥ 2f SIGNAL處對(duì)波形進(jìn)行采樣。換句話說(shuō)，我們每個(gè)正弦周期至少需要兩個(gè)樣本。讓我們首先嘗試通過(guò)在時(shí)域中思考來(lái)理解這個(gè)要求。

在下圖中，正弦波的采樣頻率遠(yuǎn)高于信號(hào)頻率。

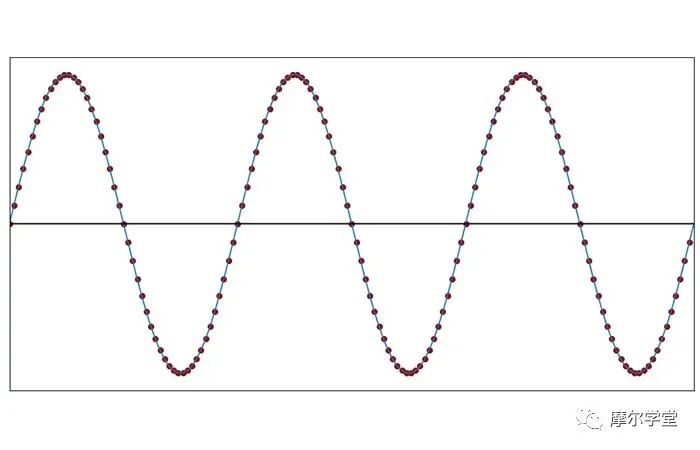
每個(gè)圓圈代表一個(gè)采樣時(shí)刻，即測(cè)量模擬電壓并將其轉(zhuǎn)換為數(shù)字的精確時(shí)刻。

為了更好地可視化此采樣過(guò)程為我們提供的內(nèi)容，我們可以繪制樣本值，然后用直線將它們連接起來(lái)。下圖中顯示的直線近似看起來(lái)與原始信號(hào)完全一樣：采樣頻率相對(duì)于信號(hào)頻率非常高，因此線段與相應(yīng)的曲線正弦曲線段沒(méi)有明顯不同。

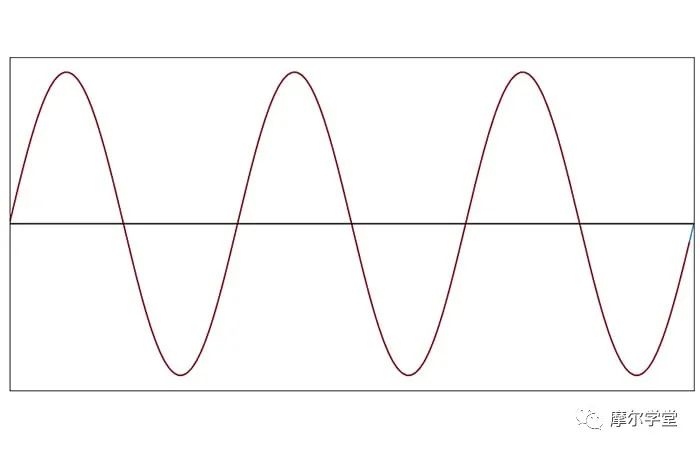
當(dāng)我們降低采樣頻率時(shí)，直線近似的外觀與原來(lái)的不同。

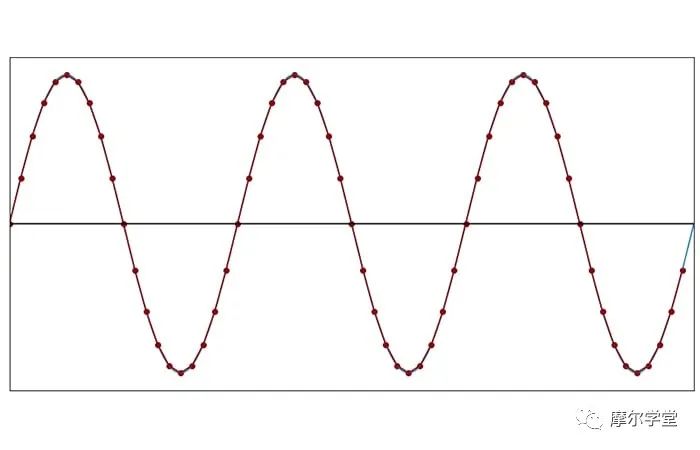
每個(gè)周期 20 個(gè)樣本（f樣本= 20f信號(hào)）

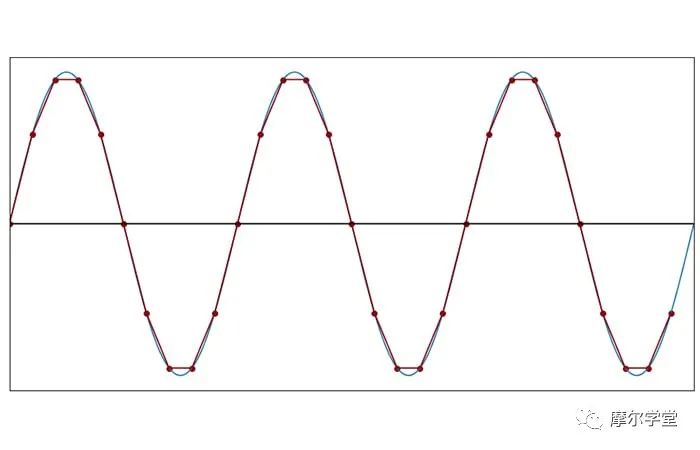
每個(gè)周期 10 個(gè)樣本（f樣本= 10f信號(hào)）

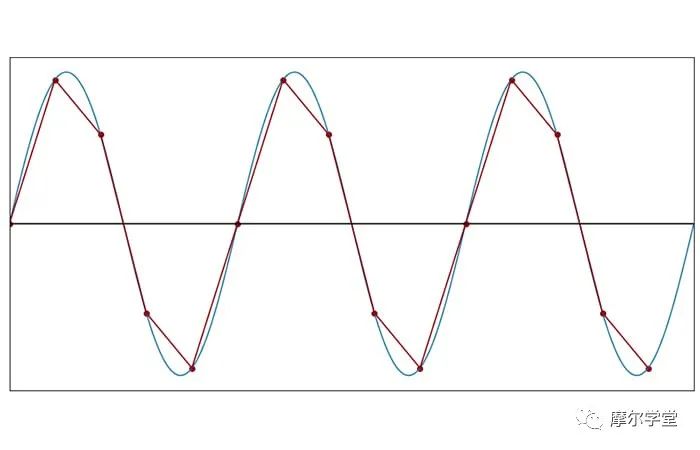
每個(gè)周期 5 個(gè)樣本（f樣本= 5f信號(hào)）

在 fSAMPLE= 5fSIGNAL時(shí)，離散時(shí)間波形不再是連續(xù)時(shí)間波形的令人滿(mǎn)意的表示。但是請(qǐng)注意，我們?nèi)匀豢梢郧宄刈R(shí)別離散時(shí)間波形的頻率。信號(hào)的循環(huán)性質(zhì)并沒(méi)有丟失。

閾值：每個(gè)周期兩個(gè)樣本

當(dāng)我們將每個(gè)周期的樣本數(shù)減少到五個(gè)以下時(shí)，采樣產(chǎn)生的數(shù)據(jù)點(diǎn)將繼續(xù)保留模擬信號(hào)的循環(huán)性質(zhì)。然而，最終我們達(dá)到了頻率信息被破壞的程度。考慮以下情節(jié)：

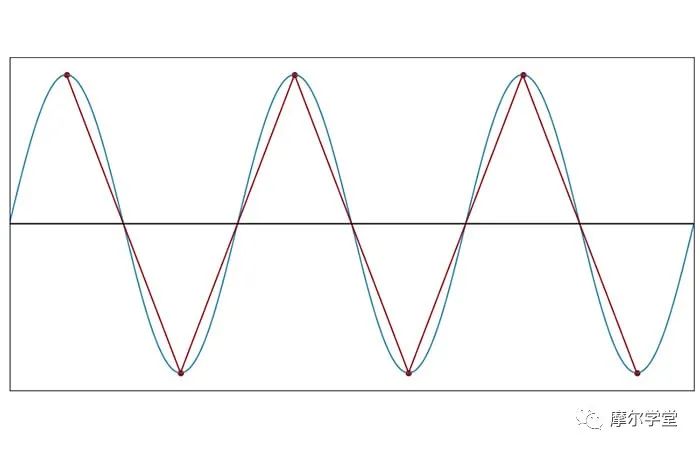
每個(gè)周期 2 個(gè)樣本（f樣本= 2f信號(hào)）

當(dāng) fSAMPLE= 2fSIGNAL時(shí)，正弦曲線形狀完全消失。盡管如此，采樣數(shù)據(jù)點(diǎn)產(chǎn)生的三角波并沒(méi)有改變正弦波的基本周期性。三角波的頻率與原始信號(hào)的頻率相同。

但是，一旦我們將采樣頻率降低到每個(gè)周期少于兩個(gè)樣本的程度，就無(wú)法再做出這種說(shuō)法。因此，對(duì)于原始波形中的最高頻率，每個(gè)周期兩個(gè)樣本是混合信號(hào)系統(tǒng)中至關(guān)重要的閾值，相應(yīng)的采樣頻率稱(chēng)為奈奎斯特速率：

如果我們以低于奈奎斯特速率的頻率對(duì)模擬信號(hào)進(jìn)行采樣，我們將無(wú)法完美地重建原始信號(hào)。

接下來(lái)的兩個(gè)圖展示了當(dāng)采樣頻率降至奈奎斯特速率以下時(shí)發(fā)生的循環(huán)等效性損失。

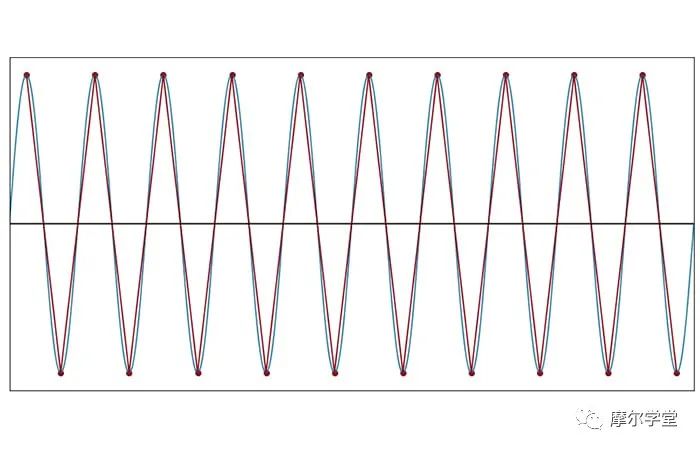
每個(gè)周期 2 個(gè)樣本（f樣本= 2f信號(hào)）

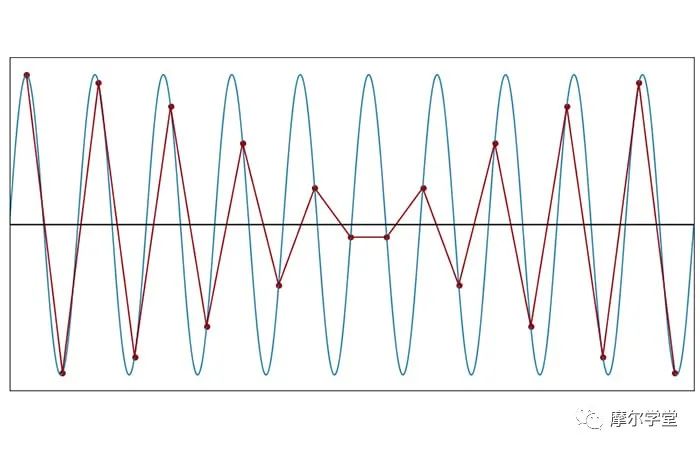
每個(gè)周期 1.9 個(gè)樣本（f樣本= 1.9f信號(hào)）

在 fSAMPLE= 1.9fSIGNAL時(shí)，離散時(shí)間波形從根本上獲得了新的循環(huán)行為。采樣模式的完全重復(fù)需要一個(gè)以上的正弦周期。

然而，當(dāng)我們每個(gè)周期有 1.9 個(gè)樣本時(shí)，采樣頻率不足的影響有點(diǎn)難以解釋。接下來(lái)的情節(jié)使情況更加明朗。

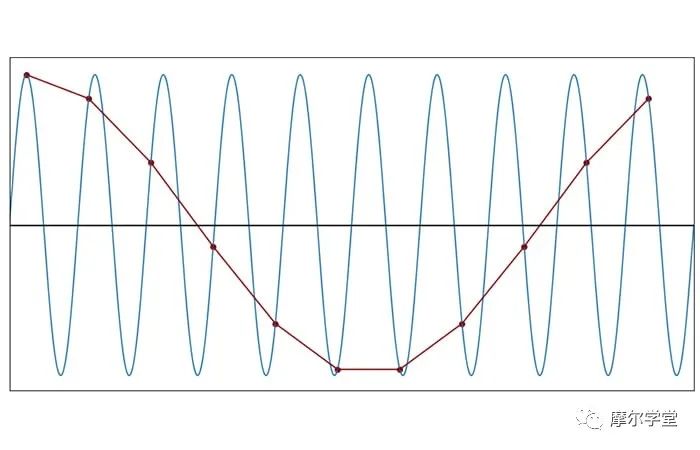
每個(gè)周期 1.1 個(gè)樣本（f樣本= 1.1f信號(hào)）

如果您對(duì)正弦曲線一無(wú)所知并使用以 1.1f SIGNAL采樣產(chǎn)生的離散時(shí)間波形進(jìn)行分析，您將對(duì)原始信號(hào)的頻率形成嚴(yán)重錯(cuò)誤的想法。此外，如果您擁有的只是離散數(shù)據(jù)，則不可能知道頻率特性已被破壞。采樣創(chuàng)建了原始信號(hào)中不存在的新頻率，但您不知道該頻率不存在。

底線是：當(dāng)我們以低于奈奎斯特速率的頻率進(jìn)行采樣時(shí)，信息將永久丟失，并且無(wú)法完美地重建原始信號(hào)。

結(jié)論

我們已經(jīng)介紹了香農(nóng)采樣定理和奈奎斯特速率，并且我們?cè)噲D通過(guò)觀察時(shí)域中采樣的影響來(lái)深入了解這些概念。




審核編輯：劉清